Декартовы прямоугольные координаты на плоскости и в пространстве

1. Обзорные лекции по математике

Володин Юрий Владимирович
доцент
кафедры прикладной математики

2. Декартовы прямоугольные координаты на плоскости и в пространстве.

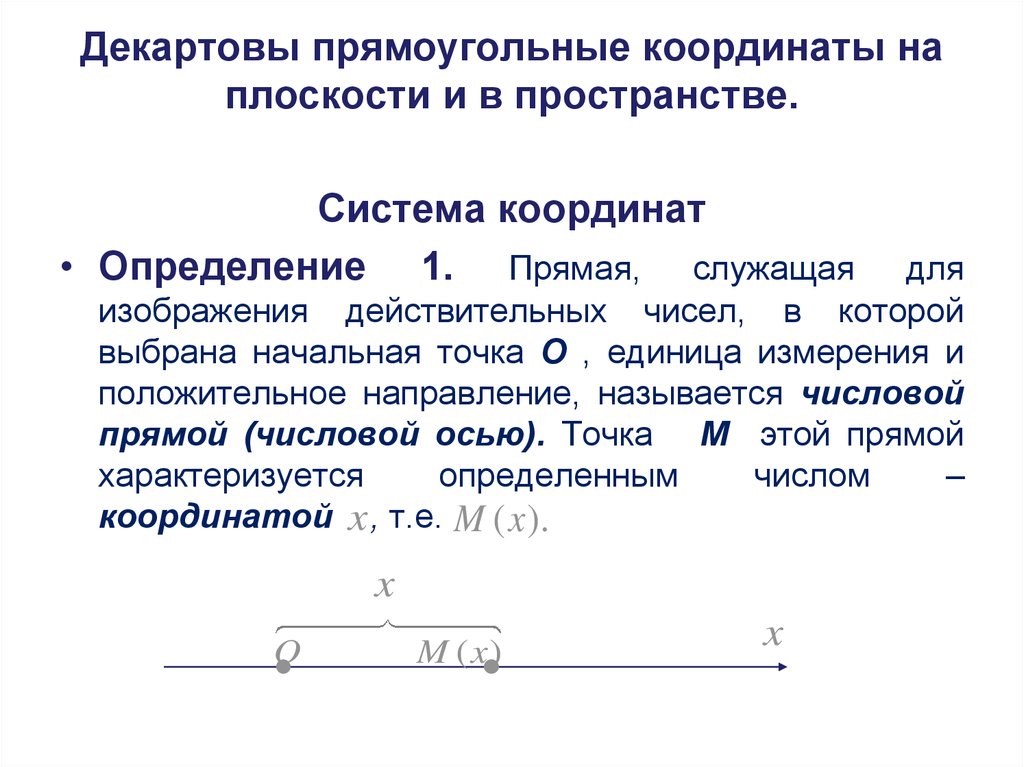
Система координат
• Определение 1. Прямая, служащая
для
изображения действительных чисел, в которой
выбрана начальная точка О , единица измерения и
положительное направление, называется числовой
прямой (числовой осью). Точка М этой прямой
характеризуется
определенным
числом
–
координатой x , т.е. M ( x ).
x
O
M ( x )
x

3.

• Определение
2.
Две
взаимно
перпендикулярные оси
Ox и Oy , имеющие
общее начало O и одинаковую единицу масштаба,
образуют прямоугольную (или декартовую)
систему координат на плоскости.
Каждой точке М этой
плоскости соответствует пара чисел
x, y , называемых ее координатами,
т.е. M ( x , y ). x называется
абсциссой, y - называется ординатой
точки М.
Y
y
O
x
M ( x, y )
x

4.

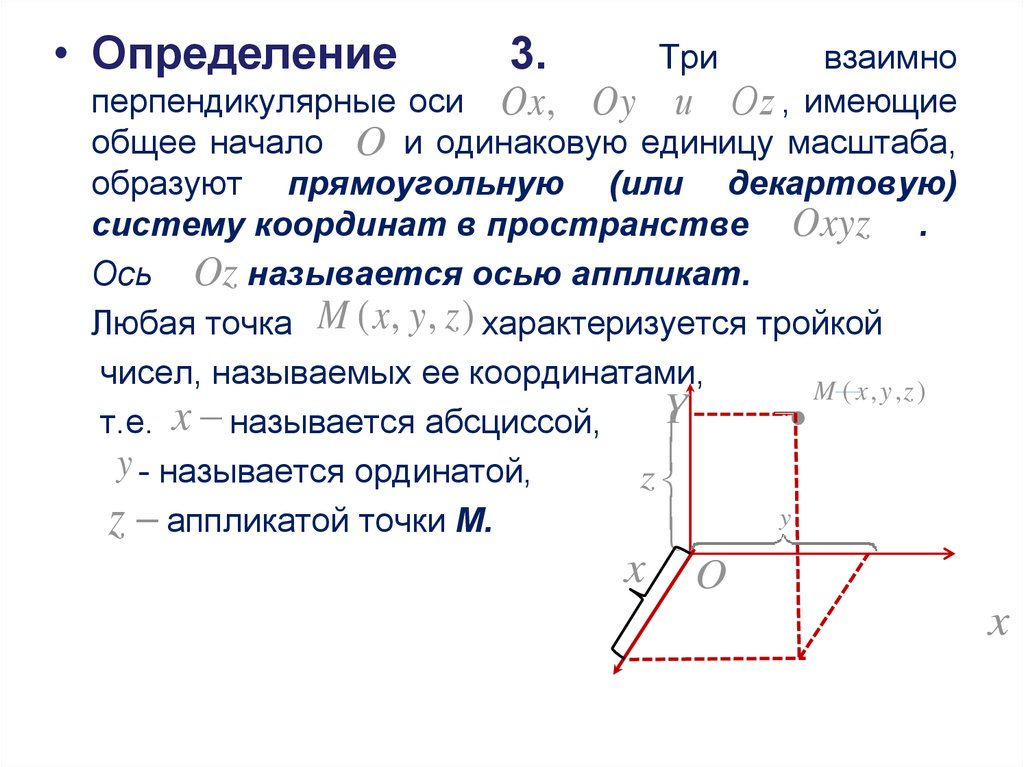
• Определение
3.
Три
взаимно
перпендикулярные оси Ox , Oy и Oz , имеющие
общее начало O и одинаковую единицу масштаба,
образуют прямоугольную (или декартовую)
систему координат в пространстве Oxyz .
Ось Oz называется осью аппликат.
Любая точка M ( x , y , z ) характеризуется тройкой
чисел, называемых ее координатами,
M ( x , y ,z )
Y
т.е. x называется абсциссой,
y - называется ординатой,
z
y
z аппликатой точки М.
x
O
x

5.

ОПРЕДЕЛЕНИЯ
AB
1. Вектором
называется направленный
отрезок с началом в точке А и концом в точке В.
2.
Длиной
(или
модулем) AB вектора
называется длина отрезка АВ. Используется
обозначение: AB .
3.
Два вектора и называются равными, если
они имеют одинаковые длины, лежат на
параллельных прямых (коллинеарны) и направлены
в одну сторону (сонаправлены).
4. Проекцией вектора a на ось Ou называются
a
число, обозначаемое
, вычисляемое по
ПрOu
формуле:
.
a
ПрOu a cos( a , Ou )

6.

ПрPR PQ PS
ПрPR PQ PS
• Определение. Если начало и конец вектора совпадают,
например 0 AA , то такой вектор называется нулевым
и обозначается AA .
Длина нулевого вектора равна нулю.

7.

• 5. Направляющими углами вектора a
называются углы между ним и координатными осями:
( a , Ox ); ( a , Oy ); ( a , Oz )
• 6. Косинусы направляющих углов называются
направляющими косинусами вектора:
cos cos( a , Ox ); cos cos( a , Oy ); cos cos( a , Oz )
• 7. Проекции вектора a на координатные оси
Ox , Oy , Oz называются координатами вектора и
обозначаются, соответственно, a x ; a y ; a z .
З а м е ч а н и е 1. Для любого вектора a верно
равенство: a a x i a y j a z k .
i ; j ; k - единичные векторы, сонаправленные с
соответствующей осью.

8.

(0,0, az )
(a x , a y , a z )
(0, a y ,0)
a
ax i
az k
(a x ,0,0)
ay j
a ax i a y j az k .
a ( a x ; a y ; a z ).
(a x , a y ,0)

9.

a ( a x ; a y ; a z ).
Вектор a также обозначается
З а м е ч а н и е 2. Для любого вектора
a a x i a y j a z k верны равенства:
ay
ax
az
cos ;cos ; cos
a
a
a
cos 2 cos 2 cos 2 1.
З а м е ч а н и е 3. У равных векторов равны
соответствующие координаты:
a b , a x bx ; a y by ; a z bz .
З а м е ч а н и е 4. У коллинеарных векторов
координаты пропорциональны:
ax a y az
a || b ,
k.
bx by bz

10.

З а м е ч а н и е 5. Длина вектора a ( a x ; a y ; a z ) через
координаты определяется по формуле:
a a 2x a y2 a 2z
Если известны координаты точек
B ( x ; y ; z ), то
b
b
b
A ( xa ; ya ; za ) и
AB ( xa xb ) 2 ( ya yb ) 2 ( z a zb ) 2 .
AB ( xa xb )i ( ya yb ) j ( z a zb ) k .

11. ОПЕРАЦИИ НАД ВЕКТОРАМИ

1) Сложение: Координаты суммы двух векторов равны
сумме соответствующих координат слагаемых
векторов.
a b
a
a b (ax bx , a y by , az bz ).
b
2) Вычитание:
b
a b
a
a b (ax bx , a y by , az bz ).

12.

3) Умножение вектора на скаляр
a ( a x ; a y ; a z )
4) Скалярное произведение двух векторов.
О п р е д е л е н и е. Скалярным произведением двух
a и
векторов
b
называется число, обозначаемое
a , b , вычисляемое по формуле a, b a b cos ,
где угол между векторами a и
Если известны координаты векторов
a (a ; a ; a ) и b (b ; b ; b ) , то
x
y
z
a ,b a b
x x
x
y
z
a y by az bz .
b.

13. Свойства скалярного произведения

• 1. a b b a
• 2.
a)( b b a
• 3. c a b c a c b
• 4.
• 5.
b a
cos
a b
Пр
a
b
a b
b
угол между двумя векторами

14. Пример

Даны векторы :
a (2; 1; 2); b (8; 4;0).
Найти:
1. с 2a; d b a;
2. длины векторов с и d ;
3. скалярный квадрат вектора d ;
4. скалярное произведение векторов с и d ;
5. угол между весторами с и d

15. Решение.

1. По определению
с 2a (4; 2; 4), d b a (6; 3;2).
2. Найдем длины векторов
a a 2x a y2 a 2z
с и
d .
По формуле
найдем
с 42 ( 2)2 ( 4)2 6, d 62 ( 3)2 22 7.
3. Скалярный квадрат равен квадрату модуля вектора, т.е.
(d , d ) d 2 49.

16.

4. Скалярное произведение
(c d ) c x d x c y d y c z d z .
(c d ) 4 6 ( 2) ( 3) ( 4) 2 22.
5. Угол между векторами
равенством:
си d
определяется
с, d 22
сos
0,52
с d
6 7
Откуда
arccos 0,52 580.