Similar presentations:
Векторы. Линейные операции над векторами. Базис. Координаты вектора. Длина вектора
1.
Векторная алгебра•Векторы. Линейные операции над векторами
•Базис. Координаты вектора
•Длина вектора
•https://www.youtube.com/watch?v=E9VUvWGsc24&t=1s
•Деление отрезка в данном отношении
•https://www.youtube.com/watch?v=paHQGE1qpdM
2.
Определение. Вектором или по-другому свободнымвектором называется направленный отрезок (т.е.
отрезок, у которого одна из ограничивающих его
точек принимается за начало, а вторая – за конец).
a
A
B
AB
Расстояние от начала вектора до
его конца называется длиной
(модулем) вектора. AB a
Вектор, длина которого равна единице, называется
единичным вектором или ортом.
Вектор, начало и конец которого совпадают, называется нулевым и обозначается 0. Нулевой вектор не
имеет определенного направления и имеет длину,
равную нулю.
3.
aabb
aa
bb
Под углом между векторами a и b будем понимать
угол, величина которого не превышает 1800.
Два вектора a и b называются ортогональными,
если угол между ними равен 900. a b
Два вектора a и b называются коллинеарными, если
они лежат на одной или параллельных прямых. a ∥ b
Три вектора, лежащие в одной или в параллельных
плоскостях, называются компланарными.
Два вектора называются равными, если они сонаправлены и имеют одинаковую длину. Все нулевые
векторы считаются равными.
4.
Определение. Произведением вектора a на число0 называется вектор, длина которого a , а
направление совпадает с направлением вектора a
при 0 и противоположно ему при 0. Если
a 0 или 0 , то их произведение полагают равным 0 .
2a
a
2a
( 1) a = a
противоположный вектору a
Лемма 2.1 (критерий коллинеарности векторов). Два
ненулевых вектора a и b коллинеарны тогда и только
тогда, когда a b, для некоторого числа 0.
5.
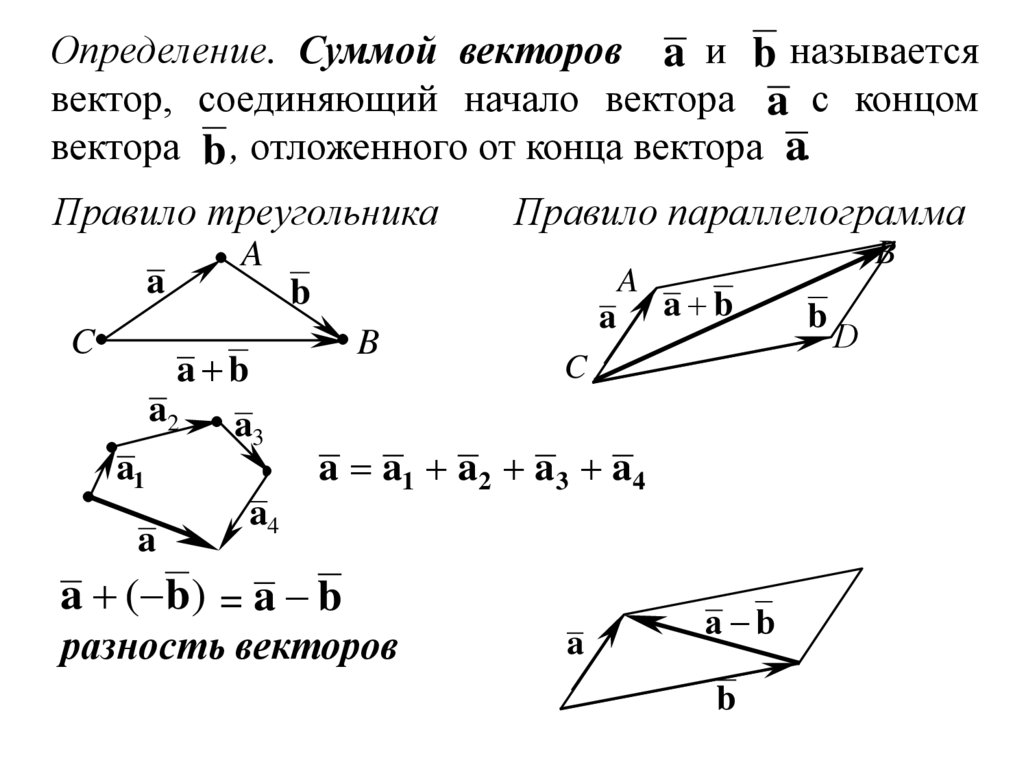
Определение. Суммой векторов a и b называетсявектор, соединяющий начало вектора a с концом
вектора b , отложенного от конца вектора a.
Правило треугольника
a
C
A
A
b
a b
a2
a3
a1
a
Правило параллелограмма
B
a
B
a b
C
a a1 a2 a3 a4
a4
a ( b ) = a b
разность векторов
a
a b
b
b
D
6.
Определение. Пусть даны векторы a1 , a2 , , ak .Тогда вектор b = 1 a1 2 a2 k ak называют
линейной комбинацией векторов a1 , a2 , , ak .
При этом говорят, что вектор b линейно выражается через вектора a1 , a2 , , ak , или другими
словами разложен по векторам a1 , a2 , , ak .
Лемма 2.2 (критерий компланарности векторов).
Три ненулевых вектора a , b и c компланарны
тогда и только тогда, когда один из них линейно
выражается через другие (например, c = 1 a + 2 b ).
7.
Свойства линейных операций над векторами1. a b b a
2. (a b) c a (b c)
3. a 0 a
4. a ( a) 0
5. ( a ) ( )a
6. ( )a a a
7. (a b) a b
8. 1a a
8.
Определение. Говорят, что векторы a1 , a2 , , akлинейно зависимы, если существуют числа 1 , 2 ,
, k , не равные нулю одновременно, такие, что
линейная комбинация 1 a1 2 a2 k ak = 0.
Если же равенство 1 a1 2 a2 k ak = 0
возможно только при условии 1 2 k 0 ,
то векторы a1 , a2 , , ak называют линейно
независимыми.
Лемма 3.1. Векторы a1 , a2 , , ak линейно
зависимы тогда и только тогда, когда хотя бы один
из них линейно выражается через оставшиеся.
9.
Лемма 3.2 (критерий линейной зависимости двухвекторов). Два ненулевых вектора a и b линейно зависимы тогда и только тогда, когда они
коллинеарны.
Лемма 3.3 (критерий линейной зависимости трёх
векторов). Три ненулевых вектора a , b и c
линейно зависимы тогда и только тогда, когда они
компланарны.
10.
Определение. Базисом некоторой системы векторовназывается
любая
максимальная
линейно
независимая подсистема этой системы векторов.
Иначе говоря e1 , e2 , , en – базис, если
1) e1 , e2 , , en – линейно независимы;
2) e1 , e2 , , en , a – линейно зависимы для любого
вектора a из данной системы векторов.
Базис можно выбрать не единственным образом.
Например, если e1 , e2 , , en – базис, то при 0
e 1 , e2 , , en – также базис.
11.
Теорема 3.4. Любые два базиса данной системывекторов состоят из одного и того же числа
векторов.
Теорема 3.5. 1) Базисом на плоскости являются
любые два неколлинеарных вектора.
2) Базисом в пространстве являются
любые три некомпланарных вектора.
Теорема 3.6 (о базисе). Каждый вектор линейно
выражается через базис, причем единственным
образом.
e1 , e2 , , en – базис, a – произвольный вектор
a 1 e1 2 e2 n en
При этом 1 , 2 , , n называют координатами
вектора a в базисе e1 , e2 , , en
12.
Зафиксируем произвольную точку O в пространствеи выберем некоторый базис.
Совокупность этой точки и этого базиса называется
системой координат.
2 e2
e2
O
1e1
a = OM = 1 e1 2 e2
a
М
e1
1 и 2 – координаты
a в этом базисе
a = OM = вектора
1 e1 2 e2
Также говорят, что 1 и 2 – координаты точки M.
13.
Декартовой прямоугольной системой координатв пространстве называют систему координат,
базисом в которой являются единичные векторы,
попарно ортогональные друг с другом.
Правая система координат, в которой векторы базиса образуют правую тройку, обозначают i , j , k :
z
k
j
i
x
Пусть a – произвольный вектор.
y
Тогда
или
a = ax i + ay j + az k
a ={ a x , a y , a z }
Замечание. Иногда в качестве базиса берут левую
тройку векторов ( i , j , - k ). Тогда такую систему
координат называют левой.
14.
Пусть в пространстве задана ось l, то естьнаправленная прямая, AB – произвольный вектор.
Обозначим через A1 и B1 – проекции на ось l
точек A и B соответственно.
B
l
A
B1
A1
Проекцией вектора AB на ось l
называется положительное число A1B1 ,
если вектор A1B1 и ось l одинаково
направлены, и отрицательное число
A1B1 , если вектор A1B1 и ось l
противоположно направлены.
Если точки A1 и B1 совпадают, то проекция вектора
AB равна 0.
пр AB
l
15.
Свойства проекций:1. Проекция вектора a на ось l равна произведению
длины вектора a на косинус угла между
вектором и осью: прl a = a cos .
2. Проекция суммы нескольких векторов на ось l
равна сумме их проекций на эту ось.
3. При умножении вектора a на число его
проекция на ось l также умножается на это число:
прl( a )= прl a .
a = ax i + ay j + az k
координата a x – это проекция вектора a на ось Ox
координата a y – проекция вектора a на ось Oy
координата a z – проекция вектора a на ось Oz.
16.
aM
az
O
ax
K
ay
N
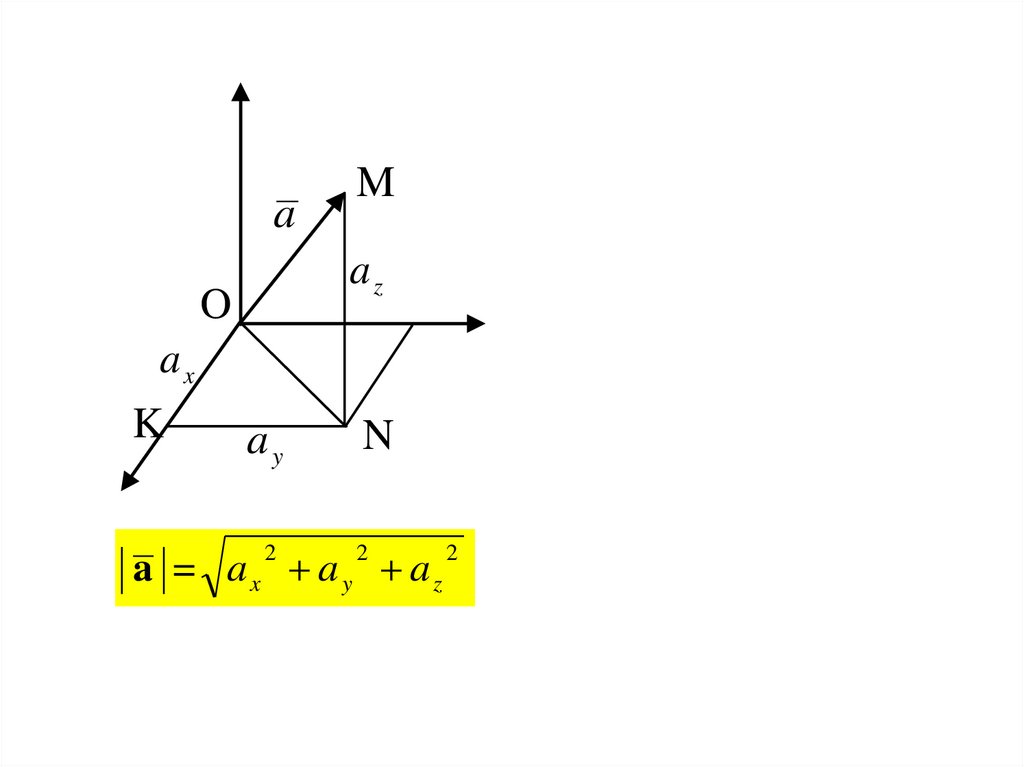
a = ax a y az
2
2
2
17.
a ={ a x , a y , a z } Рассмотрим вектор { cos , cos , cos }.a
По свойству 1 проекций
ax прOx a a cos ,
a y прOy a a cos ,
az прOz a a cos
ay
az
ax
1
{ cos , cos , cos }= i + j + k = a ,
a
a
a
a
то есть вектор { cos , cos , cos } – единичный и
направлен также, как и a . Этот вектор называют
ортом вектора a .
cos , cos , cos – направляющие косинусы вектора a
cos 2 cos 2 cos 2 1 – свойство направляющих
косинусов.
18.
Теорема 4.1. Если a ={ a x , a y , a z }, b ={ bx , by , bz }, то1) a + b = { a x + bx , a y + by , a z + bz },
2) a = { a x , a y , a z }.
19.
Лемма 4.2 (критерий коллинеарности векторов вкоординатной форме). Два ненулевых вектора a и
b коллинеарны тогда и только тогда, когда их
координаты пропорциональны.
Пример
2= 1
4= 2
0= 0
=2 векторы a и b коллинеарны
a ={2, 4, 0}
b ={1, 2, 0}
a x = bx , a y = bx , a z = bx
ay
ax
az
, =
, =
=
bx
bz
by
ay
ax
az
=
=
bx
bz
by
20.
A (x1, y1, z1), B (x2, y2, z2).Найдем координаты AB .
A (x1, y1, z1), B (x2, y2, z2). Найдем координаты AB .
A
B
O
Вектор
Вектор
= O=BO-BO–A O
. A.
ABAB
ТакТак
каккак
OBO={x
2, y22,, zy22},
, z2},
B ={x
OAO={x
1, y1,, zy1},
A ={x
1 1, z1},
то то
={x={x
ABAB
2- x1,–yx
2- ,yy
1, z2- z1}.
2
1 2 – y1, z2 – z1}.
Лемма 4.3. Если A имеет координаты (x1, y1, z1),
Лемма 4.3. Если A имеет координаты (x1, y1, z1),
очка B координаты (x2, y2, z2), то вектор AB имеет
точка B{x– координаты
(x
, yz2,}.z2), то вектор AB имеет
2–
оординаты
–
x
,
y
–
y
,
z
2
1
2
1
2
1
координаты {x2 – x1, y2 – y1, z2 – z1}.
21.
Разделим отрезок AB в отношении , то есть напрямой, проходящей через точки A и B, найдём
такую точку M, что AM MB .
1
1) =1/2, AM MB .
2
2) 2 , AM 2 MB .
A
1
А
3) 1 , то есть AM MB
M
B
2
В
– невозможно
>0 AM и MB одинаково направлены
точка M лежит внутри отрезка AB
<0 AM и MB противоположно направлены
точка M лежит вне отрезка AB
М
22.
Пусть A (x1, y1, z1), B (x2, y2, z2).Обозначим координаты точки M (x, y ,z).
Тогда AM ={x–x1, y–y1, z–z1}, MB ={x2–x, y2–y, z2–z}.
Так как AM MB , то
x –x1= (x2–x), y–y1= (y2–y), z–z1= (z2–z).
Откуда получаем, что
x
x1 x2
y y 2
z z2
, y 1
, z 1
.
1
1
1















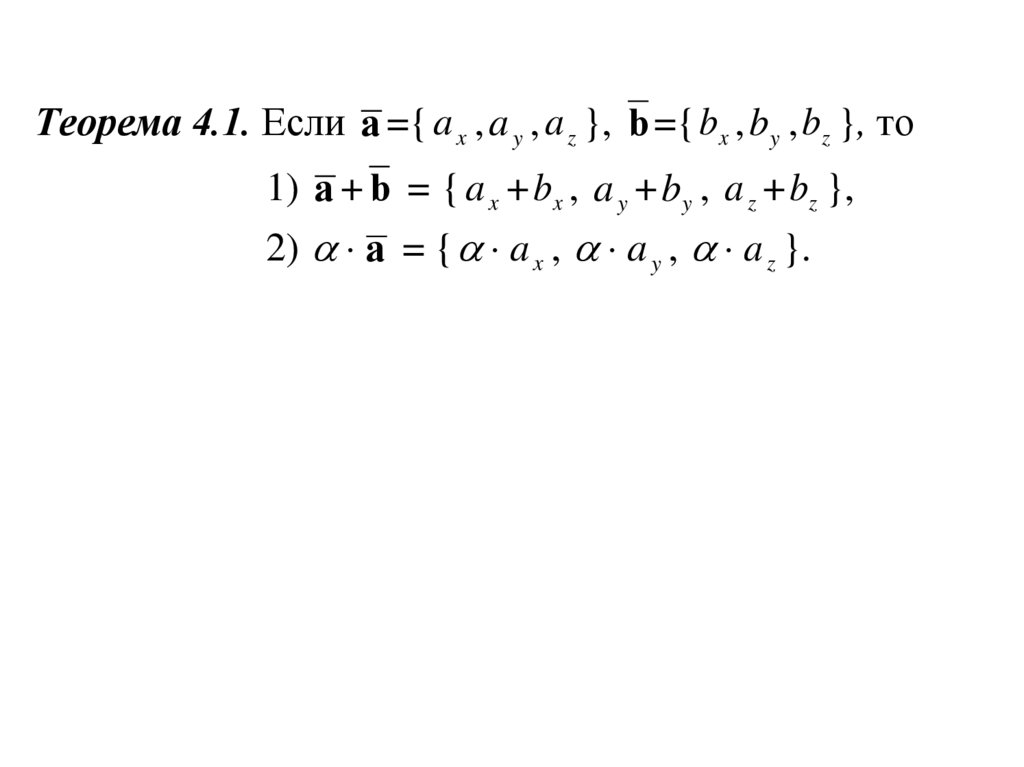




 mathematics
mathematics








