Similar presentations:
Линейные векторные пространства. Базис
1. Линейные векторные пространства. Базис
Линейные векторные пространства;Линейная зависимость векторов;
Базис и размерность пространства
Преобразование координат;
Матрица перехода
2. Линейные векторные пространства
Определение. Множество V называется линейнымвекторным пространством, если для любых его элементов
и
a
, называемых
bвекторами этого пространства, и любого
действительного числа
и
так определены в V векторы
b
a
, что верны следующиеaаксиомы:
3. Линейные векторные пространства
1. В пространстве V есть нулевой вектор 0 такой, чтоa 0 a
а V ;
2. Для любого вектора a V существует противоположный
ему вектор, обозначаемый
a , такой, что a a 0 ;
3.
a b b a а, b V ;
4.
a b c a b c а, b, c V ;
5.
1 a a
а V ;
4. Линейные векторные пространства
6.a b a b а, b V R ;
7. a a a
а V , R
a a
а V , R
8.
Пример 1. Множество всех векторов плоскости или
трехмерного
пространства
является
линейным
пространством относительно операций сложения двух
векторов и умножения векторов на число.
5. Линейные векторные пространства
nЗ а м е ч а н и е 1. Пространство R – множество строк из n
действительных чисел x1 ;...; xn – является линейным векторным
пространством, если суммой строк x1 ;...; xn и y1 ;...; y n
x1 y1 ;...; xn yn , а произведением строки
x1 ;...; xn на число назвать строку x1 ;...; xn .
нулем пространства служит строка 0 0;...;0 ; противоположной
строке а1 ;...; аn является строка а1 ;...; аn и верны все
назвать строку
аксиомы 1– 8.
6. Линейная зависимость векторов
• Определение. Векторывекторного
a1 , a 2линейного
,..., a n
пространства
называются линейно
зависимыми, если
V
существуют числа
, не все равные нулю,
1 , 2 такие,
,... n
что справедливо равенство:
.
(1 )
Определение.
линейного векторного
1a1 Векторы
a
...
a
0
2 2
n n
пространства называются
линейно
независимыми, если
a1 , a 2 ,...,только
a n при условии:
выполнение равенства (1) возможно
•.
1 2 n 0
7. Линейные векторные пространства
• Теорема. Система из k векторовпространства
a1 , a2 ,..., ak
является линейно независимой
тогда и только тогда,
n
R
когда матрица A, столбцы (строки) которой
составлены из этих векторов, имеет ранг k.
• Следствие. Система, состоящая более чем из n
векторов пространства
, линейно зависима.
Rn
8. Базис линейного пространства
L произвольное линейное пространство.Пусть
Определение. Линейная независимая система элементов
пространства e1 , eназывается
базисом этогоLпространства,
2 ,..., en
если любой элемент
пространства
является линейной
x
комбинацией этихLэлементов, т.е.
x числа
x1e1 называемые
x2e2 ,..., xnen ,
некоторые
где
координатами
x , x ,..., xэлемента
1
2
относительно базиса
n
x
e1 , e2 ,..., en .
( )
9. Базис линейного пространства
Равенствоx x1e1 x2e2 ,..., xnen , называется
( )
разложением элемента
x базису
по
e1 , e2 ,..., en .
Пример 1. В линейном пространстве всех векторов
плоскости любые два неколлинеарные вектора являются
базисом этого пространства.
Пример 2. В линейном пространстве всех векторов
пространства любые три некомпланарные вектора являются
базисом этого пространства.
10. Базис линейного пространства
Теорема. Любой элементразлагается по базису
L
единственным способом.
линейного пространства
x
этого пространства
e , e ,..., e
1
2
n
11. Базис линейного пространства
yПусть элементы x и линейного
пространства
разложены по базису e1 , e2 ,..., en :
L
x x1e1 x2e2 ... xn en ,
y y1e1 y2e2 ... yn en .
Из этих равенств, в силу аксиом 1-8 линейного векторного
пространства, получим
x y x1 y1 e1 x2 y2 e2 ... xn yn en , (1)
и
x x1e1 x2e2 ... xn en .
(2)
12. Базис линейного пространства
Равенство (1) означает, что при сложении двух элементовлинейного пространства
L
их координаты
складываются.
Равенство (2) означает, что при умножении элемента
линейного пространства
L некоторое число
на
координаты этого элемента умножаются на
.
13. Размерность линейного пространства
Определение. Если линейное пространствоL
имеет базис, состоящий из n элементов, то число n
называется размерностью линейного пространства , а
само пространство
называется n – мерным
L
линейным или векторным пространством. Размерность
линейного пространства
обозначается
через dim L.
L
L
14. Размерность линейного пространства
Линейное пространство, в котором не существует базис,назывется бесконечномерным.
Теорема. В линейном пространстве любые два базиса
содержат одинаковое число элементов.
Размерность линейного пространства всех векторов
плоскости равна двум.
Размерность линейного пространства всех векторов
пространства равна трем.
n
Размерность линейного пространства
равна
R
n.
15. Переход от одного базиса к другому
Пусть e1 , e2 ,..., eиne1 , e2 ,...,два
en произвольных
базиса n-мерного линейного пространства
Элементы
по базису
e1 , e2 ,..., en разложим
e1 , e2 ,..., en
e1 a11e1 a12 e2 ... a1n en ,
e2 a21e1 a22e2 ... a1n en
...........................................
en an1e1 an 2 e2 ... ann en .
. R
n
16. Переход от одного базиса к другому
Обозначимa11 a12 ...a1n
a21 a22 ...a1n
A
...................
an1 an 2 ...ann
Матрицу А называют матрицей перехода от нового
базиса к старому базису .
Определитель этой матрицы отличен от нуля.
17. Переход от одного базиса к другому
Замечание. Каждый векторпространства
имеет
a
L
координаты как в старом базисе, так и в новом.
Справедливо равенство:
( y1; y2 ;...; yn ) A ( x1; x2 ;...; xn )
которое связывает координаты
вектора
( x1; x2 ;...;
xn )
a
в старом базисе и координаты
базисе, где
старому.
вектора
в новом
– матрица перехода от нового базиса к
А
18. ЕВКЛИДОВЫ ПРОСТРАНСТВА.
• Определение. Скалярным произведением векторовлинейного векторного пространства
a b
обозначаемое
называется число,
L
и удовлетворяющее следующим
( a, b)
условиям:
1.
( a, b) (b, a ) а, b L
2.
( a b , c) (a, с) b, c а, b, c L
3. ( а , с ) ( a , с )
4.
( a, a ) 0
а, с L, R
а L
и
19. ЕВКЛИДОВЫ ПРОСТРАНСТВА
( a , а ) 0тогда, когда ,пространства
aнулевой
элемент
L.
Определение. Линейное векторное пространство
в котором определено скалярное произведение
векторов, называется евклидовым пространством.
Пространство
R nявляется евклидовым, так как оно
линейное векторное и в нем определено скалярное
произведение элементов.
, L
20. ЕВКЛИДОВЫ ПРОСТРАНСТВА
:.
В любом евклидовом пространстве определяют:
• длину вектора:
a a, a
• расстояние между двумя векторами:
a; b a b
• косинус угла
между
векторами
cоs
и a:
a, b
a b
b
21. Ортогональные элементы. Ортонормированный базис
Определение. Базисe1 , e2 ,...,евклидова
en
пространства
Lназывается ортогональным, если
ei , e j 0при любых
1 i j n
Определение. Ортогональный базис
e1 , e2 ,..., en
евклидова пространства
называется
L
ортонормированным, если
ei , ei 1 i 1, 2,..., n
22. ПРОЦЕСС ОРТОГОНАЛИЗАЦИИ БАЗИСА
ПРОЦЕСС ОРТОГОНАЛИЗАЦИИ БАЗИСА• Пусть –
базис
f1 , f 2 ,...,
f n в евклидовом пространстве .
Тогда векторы, вычисленные по формулам
L
k 1
где
e1 f1
e k f k c i ei
k 2,...n
образуют
ортогональный базис в
i 1
пространстве
f k ; ei
евклидовом
ci
, k 2,....n,
ei ; ei
L
23. ПРОЦЕСС ОРТОГОНАЛИЗАЦИИ БАЗИСА
ПРОЦЕСС ОРТОГОНАЛИЗАЦИИ БАЗИСАПроцесс построения указанным способом
ортогонального базиса
данному
некоторому
e1 , e2 ,..., eпо
n
называется процессом
f1 , f 2 ,..., fбазису
n
ортогонализации Шмидта.
Определение. Нормированием вектора
называется
a
а
замена его вектором
, имеющим длину, равную 1.
а
24. Примеры
Выяснить, являются ли векторыa
(1;3;1;3);
a
(2;1;1;
2);
a
(3;
1;1;1);
1
2
3
линейно зависимыми.
Решение. Составим матрицу, у которой, например,
строками являются векторы
. Приведем ее к ступенчатому виду:
a1; a2 ; a3
25. Примеры
13
1
3
2 3 ( 3)( 1) 1 2 3
1 2 3
1 1
0
5
10
:
(
5)
0
1
2
0 1 2
0 0 0
1 1
2 1
0 4 8
0 0 0
Ранг системы векторов равен двум.
Ответ : Векторы линейно зависимые.
26. Примеры
П р и м е р 2. Показать, что векторыa (1; 2; 3 ), b ( 3; 2;1) и c (1; 0;1)
3
образуют базис в пространстве R . Найти координаты вектора
m ( 1; 6;13 ) в этом базисе.
Р е ш е н и е. Составим матрицу, столбцами которой являются
данные в примере векторы. Приведем ее к ступенчатому виду:
27. Примеры
Следовательно, ранг матрицы, составленной из векторов a, b , c, равен трём; векторы a, b , c линейно независимы и образуют
базис в пространстве R 3 .
Тогда вектор
базису:
m ( 1; 6;13 ) должен разлагаться по этому
m x1a x2 b x3 c
Т.е. координаты данного разложения удовлетворяют линейной системе
алгебраических уравнений:
28. Примеры
1 x1 3x 2 x36 2 x1 2 x 2
13 3x x x .
1
2
3
1 3 1 1 ( 2)( 3)
2 2 0 6
3 1 1 13
1 1
1 3
0 4 2 8 2
0 8 2 16
29.
x1 5, x2 2, x3 030. Примеры
Итак, вектор m в базисе a, b , c имеет координаты:Отсюда заключаем:
m 5a 2b .
3
О т в е т: a, b , c – базис пространства R ;
m 5a 2b .
П р и м е р 3. Найти матрицу перехода от базиса
e1 1;1;0 , e2 2;0;1 , e3 0;1;1
к базису
5; 2;0 .
f1 1;1;1 , f 2 2;0;0 , f 3 0;0;2 .
31.
х1 , х2 , х3 , у1 , у2 , у 3 ив базисе f1 , f 2 , f 3 :
Р е ш е н и е. Найдем координаты
z1 , z 2 , z 3 векторов e1 , e2 , e3
e1 x1 f1 x2 f 2 x3 f 3 ,
e2 y1 f1 y 2 f 2 y3 f 3 ,
e3 z1 f1 z 2 f 2 z 3 f 3 .
Рассматривая каждое уравнение в отдельности, получим три
системы, соответственно, для координат х1 , х2 , х3 ,
у1 , у2 , у 3 и
z1 , z 2 , z 3 :
x1 2 x2 1
1) x1 1
x 2 x 0,
3
1
y1 2 y 2 2
2) y1 0
y 2 y 1,
3
1
z1 2 z 2 0
3) z1 1
z 2 z 1.
3
1
32.
x1 1;x2 0;
x3 1 / 2,
y1 0;
y 2 1;
y 3 1 / 2,
z1 1;
z 2 1 / 2;
z3 0.
f1 , f 2 , f 3
координаты 1;0; 1 / 2 , вектор e2 ― 0;1;1 / 2 и e3 ―
1; 1 / 2;0 .
Значит, матрица перехода от базиса e1 , e2 , e3 к базису f1 , f 2 ,
f 3 имеет вид:
Таким образом, вектор
0
1/ 2
1
1
1/ 2
0
1 1/ 2
0
e1
имеет в базисе
Ответ :
0
1/ 2
1
0
1
1
/
2
1 1/ 2
0












































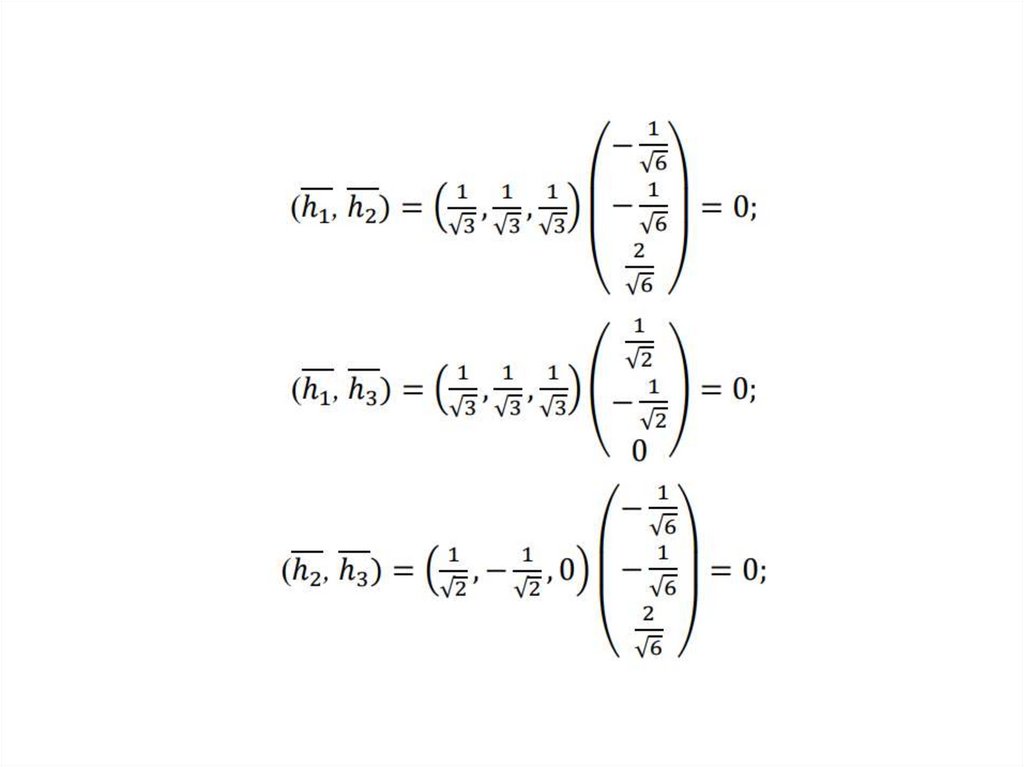

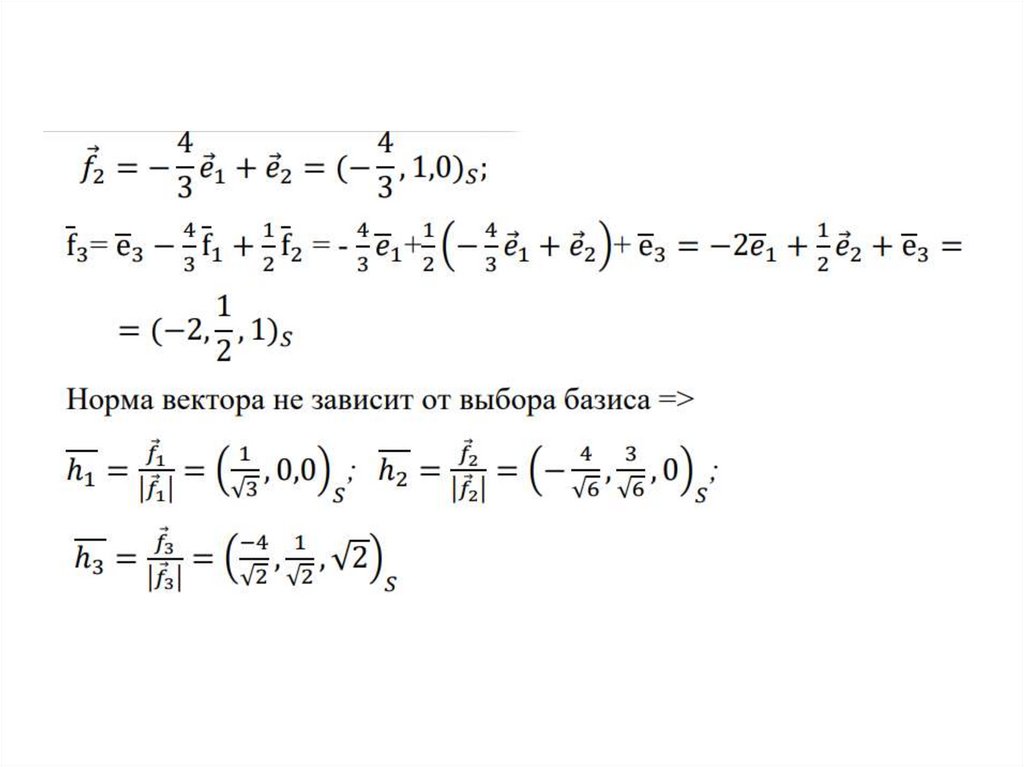







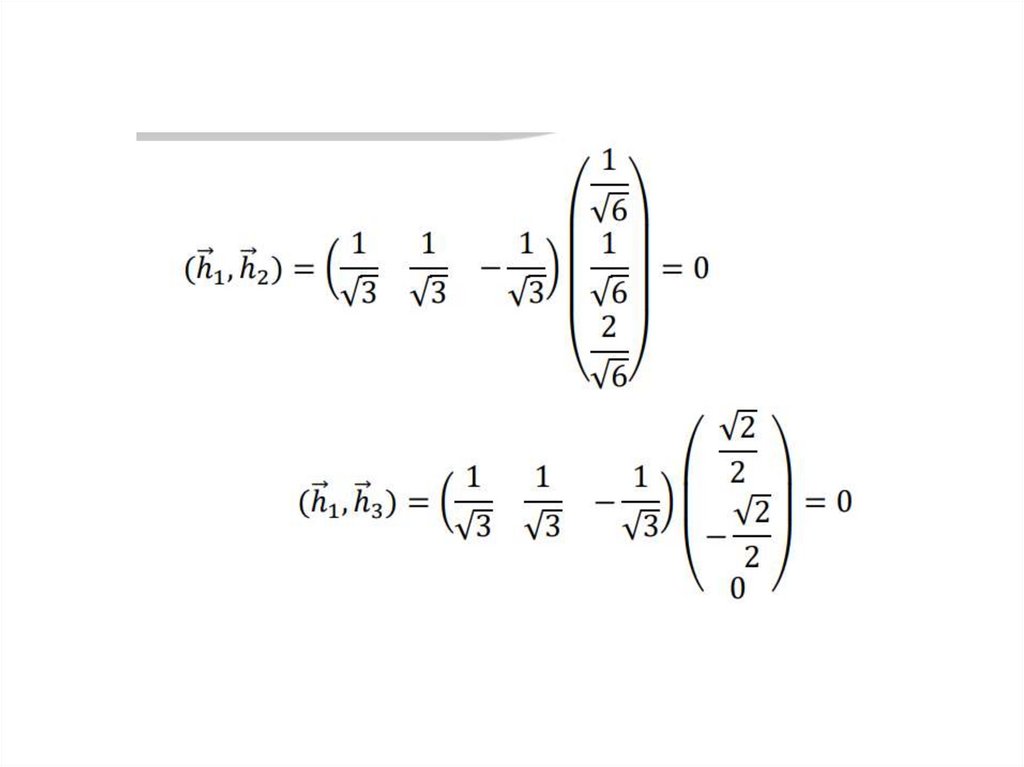
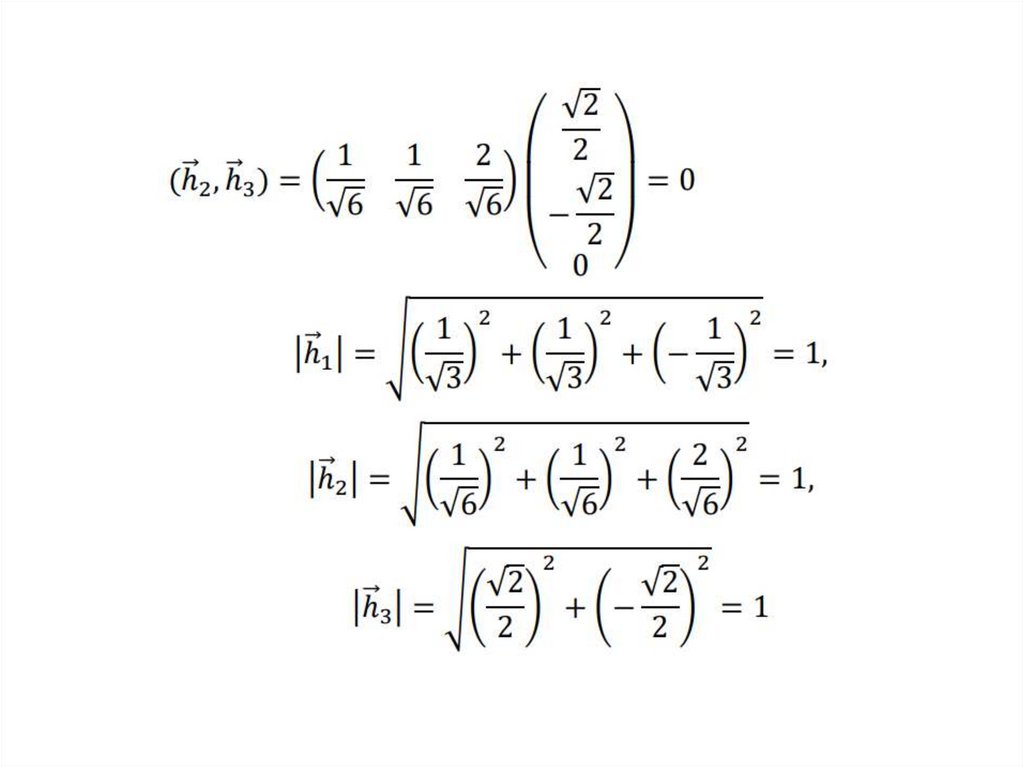

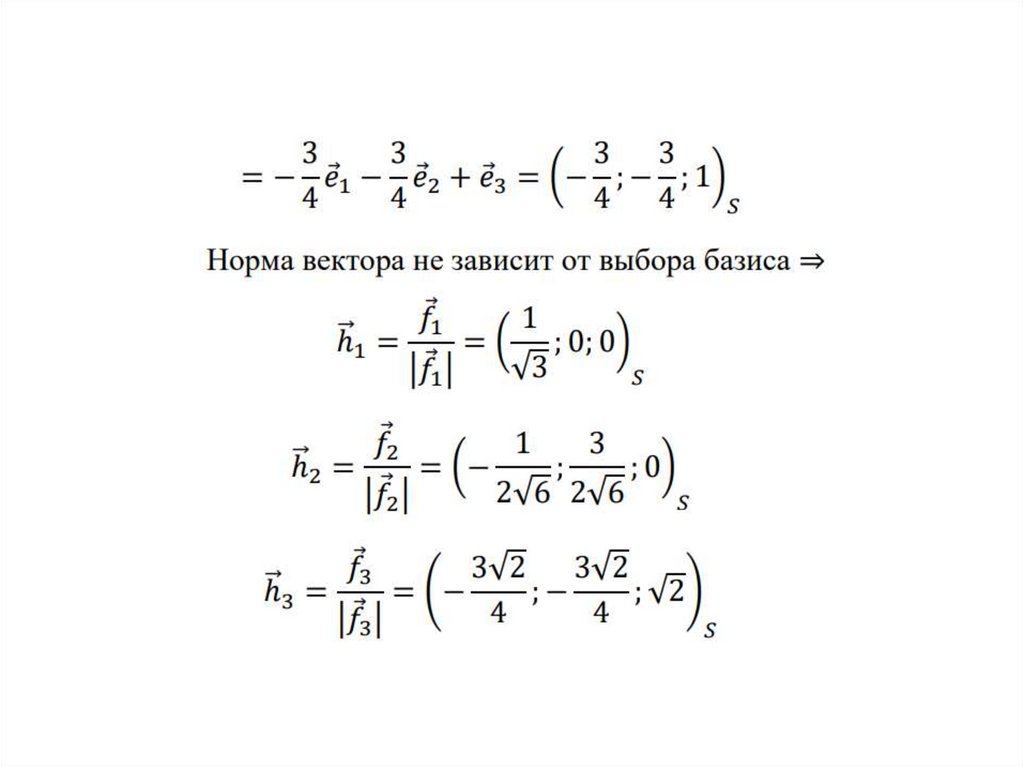



 mathematics
mathematics








