Similar presentations:
Подпространства. Базис и размерность
1. Линейная алгебра
Лекция 6Подпространства. Базис и
размерность
2. План лекции
Определение линейного подпространства nмерного координатного пространства
Линейная оболочка набора векторов
Линейное пространство решений однородной
системы линейных уравнений
Базис и размерность
Ортонормированные базисы
2
3. Векторные подпространства. Определение
Подпространством линейного пространства Rnнад полем Rназываюттакое подмножество U R n , которое обладает свойствами:
а ) x, y U x y U ;
б) x U x U .R
Другими словами, подмножество U замкнуто относительно действий
«сложения» и «умножения» на скаляр, определённых в Rn.
Тривиальными подпространствами линейного пространства Rn
называются само Rn и пространство, состоящее из одного нулевого
вектора O.
3
4. Пример
12
U X ... , 1 , 2 ,.., n R : 1 n
...
n
5. Векторные подпространства. Способ задания
Подпространством, порождённым векторамиe1 , e 2, ...e k R n ,
называют подмножество U R n всех линейных комбинаций
этих векторов (линейная оболочка набора векторов), т.е.
U e1 , e2 ,..., ek x 1e1 2e2 ... k ek , i R
5
6. Пример
1 1 1 0U 1 , 1 , 3 , 2 R 3
2 1 3 1
7. Векторные подпространства. Способ задания
Другой способ задания линейного подпространства в Rn можетслужить задание набора ограничений, которым удовлетворяют
векторы подпространства. Например, в виде A X = O.
Теорема. Множество решений однородной системы уравнений
A X = O образует линейное подпространство пространства Rn .
7
8. Пример
x1 2 x2 3 x3 4 x4 04
V X R
x1 x2 x3 x4 0
9. Базис векторного пространства. Определение
Базис векторного пространства.Q V Определение
Пусть (e , e ,..., e ) - произвольное множество векторов
1 2
s
линейного пространства Rn. Упорядоченная система векторов
называется базисом в Q, если :
а)
ek Q, k 1,2,..., s ;
б) система
(e1 , e2 ,..., es )
линейно независима;
в) для любого x Q найдутся такие числа
что
x1 , x2 ,..., xs ,
x x1e1 x2 e2 ... xs es
9
10. Размерность векторного пространства
Все базисыM e1 , e2 , ... , en V
пространства V
имеют одинаковое число векторов, которое называется
размерностью векторного пространства V и обозначается
n dim( V )
Полагают, что размерность тривиального пространства
(состоящего из одного только нулевого вектора), равна нулю:
dim(O)= 0.
Размерность подпространства, заданного СЛУ, равна n –
rg(A).
10
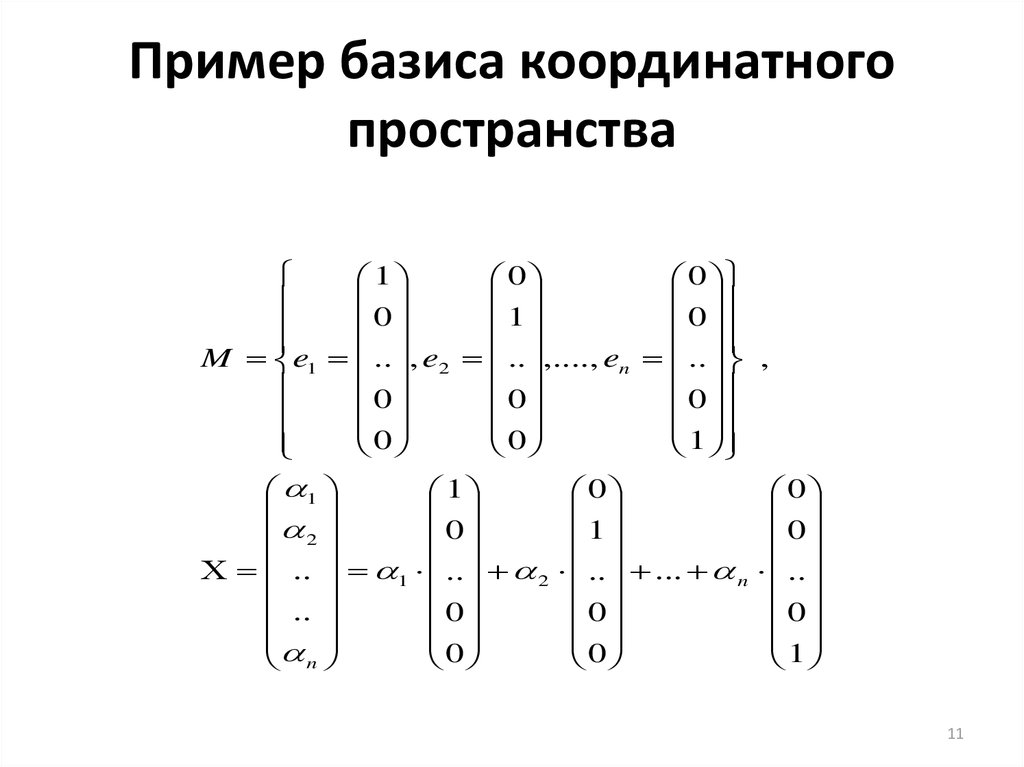
11. Пример базиса координатного пространства
10
0
0
1
0
M e1 .. , e2 .. ,...., en ..
0
0
0
0
0
1
1
1
0
2
0
1
.. 1 .. 2 .. ... n
..
0
0
0
0
n
,
0
0
..
0
1
11
12. Теоремы о базисах
1. В любом ненулевом подпространствекоординатного пространства существует
базис.
2. Если размерность подпространства
координатного пространства равна k, то
любая линейно независимая система из k
векторов образует базис этого
подпространства.
13. Нахождение базиса подпространства
Для нахождения базиса в подпространстве, порожденном некоторойсовокупностью векторов, достаточно выбрать из системы образующих
векторов линейно независимую систему.
Например,
1 1 1 0
U 1 , 1 , 3 , 2 R 3
2 1 3 1
1 1
U 1 , 1 , dim( U ) 2
2 1
25.06.2018
Векторные пространства
13
14. Алгоритм построения базиса в
n1.
2.
3.
U R
Столбцы, порождающие подпространство, записать в матрицу.
Элементарными преобразованиями над столбцами привести эту
матрицу к «ступенчатому» виду.
Ненулевые столбцы данной «ступенчатой» матрицы и будут
составлять базис исходного подпространства, а ранг матрицы будет
равен размерности этого подпространства.
U
1 1
1
2 2
2
.. , .. , ... , ..
.. ..
..
n n
n
1 1
2 2
.. ..
.. ..
n n
.. ..
.. ..
.. ..
.. ..
.. ..
1 0
1
c2 1
2
.. ..
..
cr d r
..
.. ..
n
cn d n
0 0
.. 0 0 0
.. ... .. ..
.. 1 0 0
.. .. .. ..
.. f n 0 0
.. 0
14
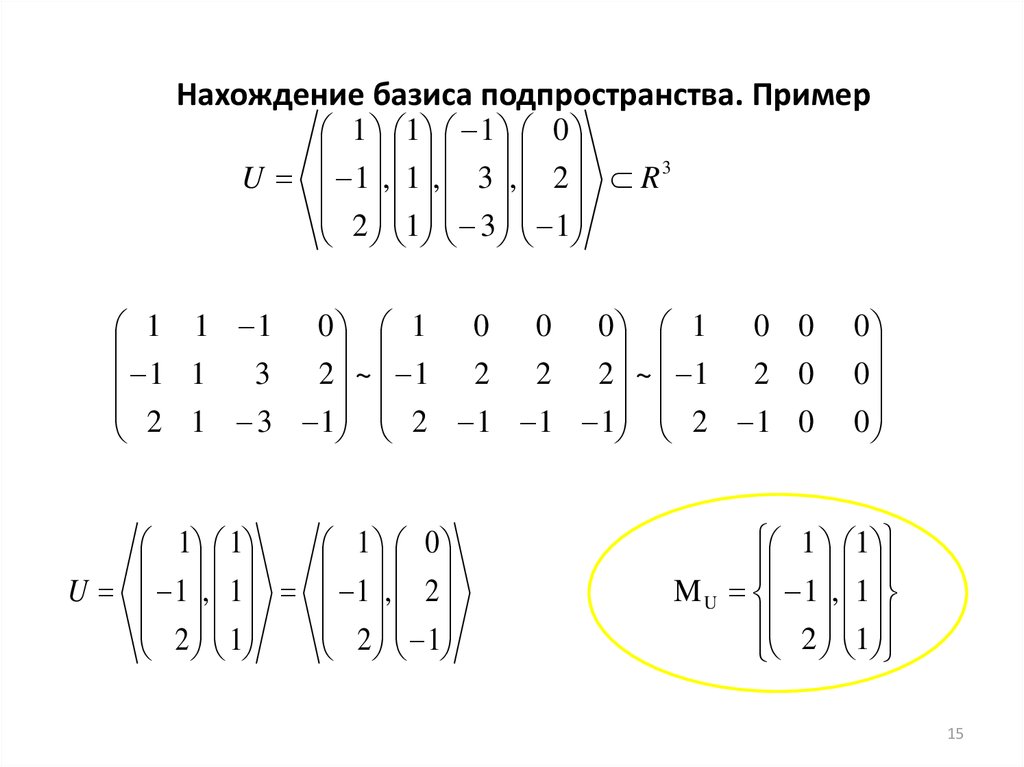
15. Нахождение базиса подпространства. Пример
1 1 1 0U 1 , 1 , 3 , 2 R 3
2 1 3 1
1 1 1 0 1 0 0 0 1 0 0
3
2 ~ 1 2 2 2 ~ 1 2 0
1 1
2 1 3 1 2 1 1 1 2 1 0
1 1
1 0
U 1 , 1 1 , 2
2 1
2 1
0
0
0
1 1
M U 1 , 1
2 1
15
16. Нахождение базиса подпространства. Пример
x1 2 x2 3x3 4 x4 04
V X R
x
x
x
x
0
1
2
3
4
6 5
x1 6 5
1 2 3 4 1 2 3 4
5 4
x2 5 4
~
X
x3
0
1
1 1 1 1 0 1 4 5
x
1 0
4
6 5
5 4
M V ,
0 1
1 0
16
17. Координаты вектора в базисе
Пусть даны M e , e ,..., e V – базис векторного пространства V1
2
n
и вектор X из V.
Координатами вектора Х в этом базисе называют коэффициенты в
разложении:
X 1e1 2e2 ... nen V
17
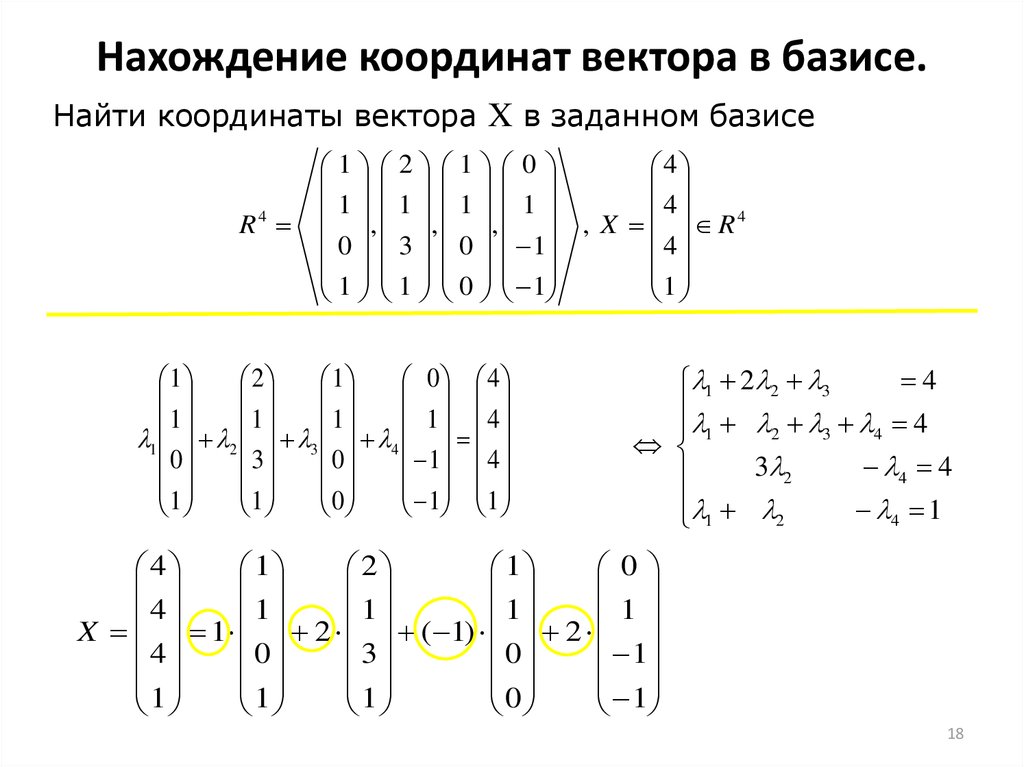
18. Нахождение координат вектора в базисе.
Найти координаты вектора X в заданном базисеR4
1
1
0 ,
1
2 1 0
4
1 1 1
4
4
,
,
,
X
R
4
3 0 1
1
1 0 1
1
2
1
0 4
1
1
1
1 4
1 2 3 4
0
3
0
1
4
1
1
0
1 1
4
1 2 2 3
4
2
3
4
1
3 2
4 4
1 2
4 1
4
1
2
1
0
4
1
1
1
1
X 1 2 ( 1) 2
4
0
3
0
1
1
1
1
0
1
18
19. Ортогональный базис
Определение.Базис
e , e ,..., en
n-мерного пространства называется
ортогональным, если
1
2
(ei , e j ) 0, i j , i, j 1,2, ... , n
Другими словами,
ортогональным базисом называется базис, состоящий
из попарно ортогональных векторов.
19
20. Ортонормированный базис
Определение.Базис
e , e ,..., en
n-мерного пространства называется
ортонормированным, если
1
2
0, i j
(ei , e j ) ij
, i, j 1,2, ... , n
1, i j
Другими словами,
ортонормированным базисом называется базис,
состоящий из попарно ортогональных векторов,
каждый из которых имеет длину, равную единице.
20
21. Построение ортогонального базиса
Построение ортогональногоЗадача.
базиса
Проверить ортогональность системы векторов
1
2
e1 ,
1
3
e2
2
1
R4
3
1
4
и дополнить ее до ортогонального базиса в R .
1. Вычислим скалярное произведение (e1,e2):
e1, e2 1 2 2 1 1 3 3 1 0
e1 e2 .
2. Задача сводится к построению векторов e3 и e4 таких, что e3 e4 и
оба ортогональны
e1, e2 .
21
22. Построение ортогонального базиса (продолжение)
Для определенияe
3
x1
x
2
x
3
x
4
частное решение системы
достаточно найти какое-либо
e3 , e1 0
e3 , e2 0
x1 2 x2 x3 3 x4 0
.
2 x1 x2 3 x3 x4 0
1 2 1
2 1 3
3 1 2 1 3 1 2 1 3
~
~
1 0 5 5 5 0 1 1 1
Выберем частное решение
e
3
4
2
.
1
3
e
3
с1 с2
с1 с2
.
с1
с
2
22
23. Построение ортогонального базиса (продолжение)
x1x
Для определения e4 2 достаточно найти какое-либо
x
решение системы
3
x
4
x1 2 x2 x3 3 x4 0
e4 , e1 0
2 x1 x2 3 x3 x4 0 ,
e4 , e2 0
4 x 2 x x 3 x 0
e , e 0
1
2
3
4
4 3
3 1 2 1
3 1 2 1
3
1 2 1 3 1 2 1
1 3 1 ~ 0 5 5 5 ~ 0 1 1 1 ~ 0 1 1 1
2
4 2 1 3 0 6 3 15 0 2 1 5 0 0 1 3
2с1
4с1
e
Общее решение , выберем
4
3с
1
с
1
2
4
.
3
1
23







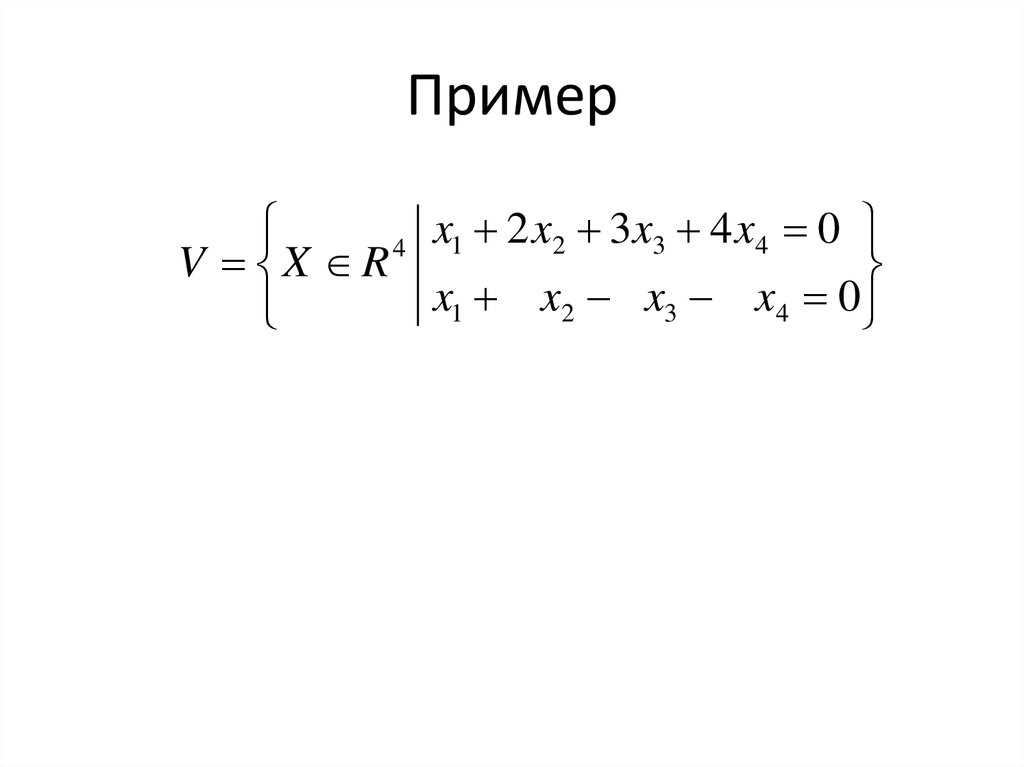












 mathematics
mathematics








