Similar presentations:
Поля и линейные пространства
1. Поля и линейные пространства
2. Обозначения
Заглавные латинские буквы (A, …)- множестваПрописные латинские буквы (a,b…) –
элементы множества
объединение множеств
пересечение множеств
декартово произведение
множеств
3. Поле
Определение. Множество К называетсяполем, если в нем введены две бинарные
операции: сложение : K K K и
умножение : K K K
удовлетворяющие аксиомам:
1.Коммутативность сложения
a b b a, a, b K
4.
2. Ассоциативность сложения(a b) c a (b c), a, b, c K
3.Существование нуля :
0 K : a 0 a, a K
4. Существование противоположного
элемента :
a K b K : a b 0
(b : a )
5.
5. Коммутативность умножения :ab ba, a, b K
6. Ассоциативность умножения
(ab)c a (bc) a, b, c K
7. Дистрибутивность :
a (b c) ab ac, a, b, c K
8. Существование единицы :
1 K , 1 0 : 1 a a, a K
9.Существование обратного элемента
1
a K , a 0 b K : a b 1 (b : a )
6. Простейшие свойства поля
1.2.
3.
4.
Нулевой элемент единственный
Противоположный элемент единственный.
Единичный элемент единственный.
Обратный элемент единственный.
7. Определение вычитания и деления в поле
Определение.a b : a ( b)
a
1
: a b
b
Замечание. Такое определение корректно,
благодаря единственности
противоположного и обратного элемента.
8. Примеры полей
Множество R – вещественных чисел являетсяполем
Множество Q - рациональных чисел является
полем.
Множество F2 ={0,1} – из двух элементов
является полем
9. Линейное пространство.
Определение. Множество V называетсялинейным пространством над полем K,
если в нем введены две бинарные
операции: сложение : V V V и
умножение на число из поля : K V V
удовлетворяющие аксиомам:
10.
1.Коммутативность сложенияa b b a , a , b V
2. Ассоциативность сложения :
(a b) c a (b c), a, b, c V
3.Существование нуля :
0 V : a 0 a , a V
11.
4.Существование противоположногоэлемента : a V b V : a b 0
5.Умножение на 1 из поля :
1 a a , a V
6. Дистрибутивность : ( )a a a
7. (a b) a b
8. ( a ) ( )a, , K , a, b V
12. Простейшие следствия из аксиом ЛП
1. Нулевой элемент единственный.2. Противоположный вектор единственный.
Определение: a b : a ( b)
3. 0 a 0, a V
4. a ( 1)a, a V
5. 0 0, K
13. Линейная комбинация векторов
V- ЛПa1, a 2 a n V набор векторов
1, 2 n K набор чисел
Определение. Выражение вида
n
1 a1 2 a 2 n an i ai
i 1
называется линейной комбинацией векторов
14. Линейная оболочка векторов
Определение. Пусть a1, a2 , an - системавекторов. Множество всех линейных
комбинаций данной системы векторов
называют линейной оболочкой системы
векторов: a1 , a 2 a n
15. Выражение вектора через линейную комбинацию
Определение. Если некоторый вектор a Vпредставлен в виде
a 1 a1 2 a 2 n a n
то говорят, что вектор a линейно выражается
через вектора a1 , a 2 a n
16. Линейная зависимость
Определение. Система векторов называетсяa1, a2 an линейно зависимой, если
существует ненулевой набор чисел
1, 2 , n таких, что
1 a1 2 a 2 n a n 0
17. Линейная независимость
Определение. Система векторов a1, a2 a nназывается линейно независимой, если
1 a1 2 a2 n an 0
тогда и только тогда, когда все числа 1, n
равны нулю.
18. Алгебраические свойства систем линейных векторов.
1. Если система векторов содержит нулевойвектор, то она линейно зависима.
2. Если часть системы векторов (подсистема)
линейно зависима, то и вся система
векторов тоже линейно зависима.
3. Система векторов линейно зависима тогда
и только тогда, когда существует вектор,
линейно выражающийся через остальные
вектора
19. Геометрические свойства систем векторов.
1. Система состоящая из одного векторалинейно зависима тогда и только тогда,
когда этот вектор нулевой.
2. Система состоящая из двух векторов
линейно зависима тогда и только тогда,
когда вектора коллинеарны.
3. Система состоящая из трех векторов
линейно зависима тогда и только тогда,
когда три вектора компланарны.
20. Базис линейного пространства
V – ЛПОпределение. Система векторов e1, e2 en ,
ei V называется базисом ЛП V,
если эта система ЛНЗ и любой вектор из V
линейно выражается через e1 , e 2 e n
Замечание. В ЛП V базис определяется не
единственным образом (можно выбрать
несколько базисов), но количество базисных
векторов n остается неизменной величиной.
21. Размерность линейного пространства
Определение. Количество векторов в базисеназывается размерностью линейного
пространства V.
Обозначение. dimV=n.
22. Координаты вектора в базисе
Из определения базиса ЛП V следует, чтолюбой вектор в этом ЛП линейно
выражается через базисные векторы :
x 1 e1 2 e2 n en
Определение. Координатами вектора x
называются коэффициенты в разложении
по базисным векторам: x ( , )
1
2
n
23. Координаты вектора в базисе
Замечание. Координаты вектора x зависят отвыбора базиса. В разных базисах у одного и
того же вектора x разные координаты.
24. Подпространства линейного пространства
25. Подпространства и подмножества
Определение. Подмножество W линейногопространства V называется линейным
подпространством, если оно является
линейным пространством относительно
операций из V.
Обозначение. W V
Утверждение. W , 0 W (ноль принадлежит
любому подпространству)
Утверждение. Для любого линейного
пространства V подмножества {0} и V являются
подпространствами.
26. Примеры подпространств.
V R2
W1 { y 3x}
W2 { y 3x 1}
27. Равносильное определение.
Утверждение. Множество W являетсялинейным подпространством V тогда и
только тогда, когда оно замкнуто
относительно операций сложения и
умножения на число:
x y W , x, y W
x W , x W , K
28. Подпространства матриц
ПустьV Mat( n n, R )
W1 { A V : At A (aij a ji )}
W2 { A V : At A (aij a ji )}
W1 – симметрические матрицы
W2 – кососимметрические матрицы
29. Подпространства C[a,b]
Пусть V=C[a,b] – пространство непрерывныхфункций на отрезке [a,b]
1
W1 C [a, b]
W2 C 2 [a, b]
W C [a, b]
W W2 W1 V
30. Пересечение и объединение подпространств
Пусть V – ЛП, W1, W2 – подпространства VОпределение.
W1 W2 {x: x W1 и x W2}
Утверждение. Пересечение подпространств
является подпространством.
Замечание. Объединение подпространств
W1 W2 {x : x W1 или x W2}
не является подпространством.
31. Сумма подпространств
Определение.W1 W2 {x w1 w2 , w1 W1, w2 W2}
Утверждение. Сумма двух подпространств
является подпространством.
Замечание. Разложение произвольного
вектора из W1+W2 по W1 и W2 возможно не
единственным образом.
32. Пример суммы подпространств
Пример. W1=XOYW2=YOZ
W1+W2=R3
Поскольку для любого вектора возможно
разложение:
x ( i j ) ( j k )
33. Прямая сумма подпространств
Определение. Пространство V называетсяпрямой суммой подпространств W1 и W2, если
V=W1+W2 и любой вектор x представим в виде
x=w1+w2 единственным образом.
Обозначение. V W W
1
2
Пример. R 2 OX OY
Поскольку разложение x i j
единственнно
34. Теорема о размерности
Теорема. Пусть V=W1+W2. ТогдаdimV dimW1 dimW2 dimW1 W2
Доказательство.
Пусть e1, e2….ek - базис W1∩W2 .
dim(W1∩W2 )=k
e1, e2….ek, a1, a2…. aℓ - базис W1, dimW1=k+ℓ
e1, e2….ek, b1, b2…. bm - базис W2, dimW2=k+m
Для доказательства теоремы достаточно
проверить, что e1, e2….ek, a1, a2…. aℓ b1, b2…. bm
- базис V
35. Доказательство
1. Проверим, что e1, e2….ek, a1, a2…. aℓ b1,b2…. bm ЛНЗ система векторов
1e1 k e k 1 a1 a 1b1 m b m 0
1e1 k ek 1a1 a 1b1 mbm
Левая часть последнего равенства
принадлежит W1, правая часть
принадлежит W2, следовательно и левая
и правая части принадлежат W1∩W2, это
значит, что правую часть можно выразить
через базис пересечения.
36. Доказательство
1b1 mbm 1e1 k ekСледовательно,
1e1 k ek 1b1 mbm 0
Следовательно,
1 2 m 0
(*)
( Поскольку вектора e1, ek , b1, bm ЛНЗ
как базис W2 )
37. Доказательство
Следовательно,1e1 k ek 1a1 a 0
Следовательно,
1 k 1 0
(**)
( Поскольку e1, ek , a1, a ЛНЗ как базисW1 )
Из (*) и (**) следует, что
e1, ek , a1, a , b1, bm ЛНЗ
38. Доказательство
2. Проверим, что любой вектор из ЛП Vлинейно выражается через систему e1,…ek,
a1,…aℓ, b1…bm.
V W1 W2
x ( 1 e1 k ek 1 a1 a )
bm )
( 1 e1 k ek 1 b1 m
□
39. Теоремы о прямой сумме
Теорема 1. Пусть V=W1+W2. Тогда V W1 W2Тогда и только тогда, когда ноль
раскладывается единственным образом:
0 0 0 .
Теорема 2.
V W1 W2 W1 W2 {0}
40. Изменение координат вектора при замене базиса
41. Матрица перехода
V – линейное пространствоe1, e2,e3…..en – первый базис (1)
e’1, e’2,e’3,…e’n – второй базис (2)
(количество векторов n=dimV, но сами
вектора разные)
Выразим вектора второго базиса через
вектора первого базиса:
42.
e' t e t e t en1 n
1 11 1 21 2
e' t e t e t e
n2 n
(3)
2 12 1 22 2
'
en t1n e1 t2n e2 t nnen
выражение вект оров вт орого базиса
через вект орапервогобазиса
43.
t11 t12 t1nt21 t22 t2n
T1 2
(4)
t
t
t
nn
n1 n 2
м ат рица перехода от первого базиса
ко вт ором у
44.
Формулу (3) можно переписатьв матричной форме:
'
'
'
e1, e2 , en e1, e2 , en T1 2 (5)
или
e' eT1 2
45. Изменение координат вектора
x V x x1e1 x2e2 xn enx1
или в м ат ричномвиде: x e1, e2 en
x
n
в другомбазисе: x x1' e1' x2' e2' xn' en'
x'
1
' '
'
или в м ат ричном виде: x e1, e2 , en
'
xn
46.
Используяформ улу (5) получаем:'
x
x
1
1
e1, e2 en e1, e2 en T1 2
x
'
x
n
n
'
x
x
1
1
T1 2
'
x
xn
n
(6)
47.
Из формулы(6) следует:x'
x1
x1
1
1
(T1 2 ) T2 1
'
xn
xn
xn
(7 )
48. Изоморфизм линейных пространств
49. Определение изоморфизма
V1, V2 – два ЛПОпределение. Пространство V1 изоморфно
V2, если существует взаимно-однозначное
соответствие f: V1→V2 такое, что
f(x1+x2)=f(x1)+f(x2) и f(αx1)=αf(x1) для
любых x1, x2 принадлежащих V1, α
принадлежащих K.
Обозначение. V1 V2
50. Свойства изоморфизма
1. Рефлективность V V2. Симметричность V1 V2 V2 V1
3. Транзитивность
V1 V2 , V2 V3 V1 V3
51.
Утверждение. Если V1 изоморфно V2, тоf(0v1)=0v2 (при изоморфизме ноль
переходит в ноль)
Доказательство.
f (0V1 ) f (0 x) 0 f ( x) 0V2
52.
Теорема. V изоморфно W тогда и толькотогда, когда dimV=dimW.
Доказательство.
1. Пусть V W , e1, e n базис V . Покажем, что
f (e1 ), f (e2 ) f (en ) базис W .
Составим ЛК :
1 f (e1 ) 2 f (e 2 ) n f (e n ) 0W
Подействуем обратной биекцией:
f 1 ( 1 f (e1 ) 2 f (e2 ) n f (en )) f 1 (OW )
53.
1 e1 2 e 2 n e n 0V 1 0, n 0f (e1 ), f (e 2 ), f (e n ) ЛНЗ.
Теперь проверим, что w W
можно выразить через
f (e1 ), f (e 2 ), f (e n )
1
f ( w) v 1 e1 n e n
1
Тогда w f ( f ( w)) f ( 1 e1 n e n )
1 f (e1 ) n f (e n )
Следовательно, f (e1 ), f (en ) базис W ,
dim W n
54.
2. Обратно, пусть dim V dim W n.Пусть e1, en базис V , e1' , en' базис W .
Тогда отобржение f (e1 ) e1' f (en ) en'
устанавливает изоморфизм между V и W
(самостоятельно проверитьсвойства).
ЧТД
55.
Утверждение. Любое линейное пространстворазмерности n изоморфно n-мерному
координатному пространству Rn.
Доказательство.
Всякий вектор v=α1e1+…αnen принадлежащий
ЛП V изоморфен вектору с координатами
(α1,….αn)
(Выполнение свойств изоморфизма
проверить самостоятельно)




























![Подпространства C[a,b] Подпространства C[a,b]](https://cf.ppt-online.org/files/slide/w/WeUVS6ryCTLigRN42Am0c5PsapfxnjK9OFZY3B/slide-28.jpg)

















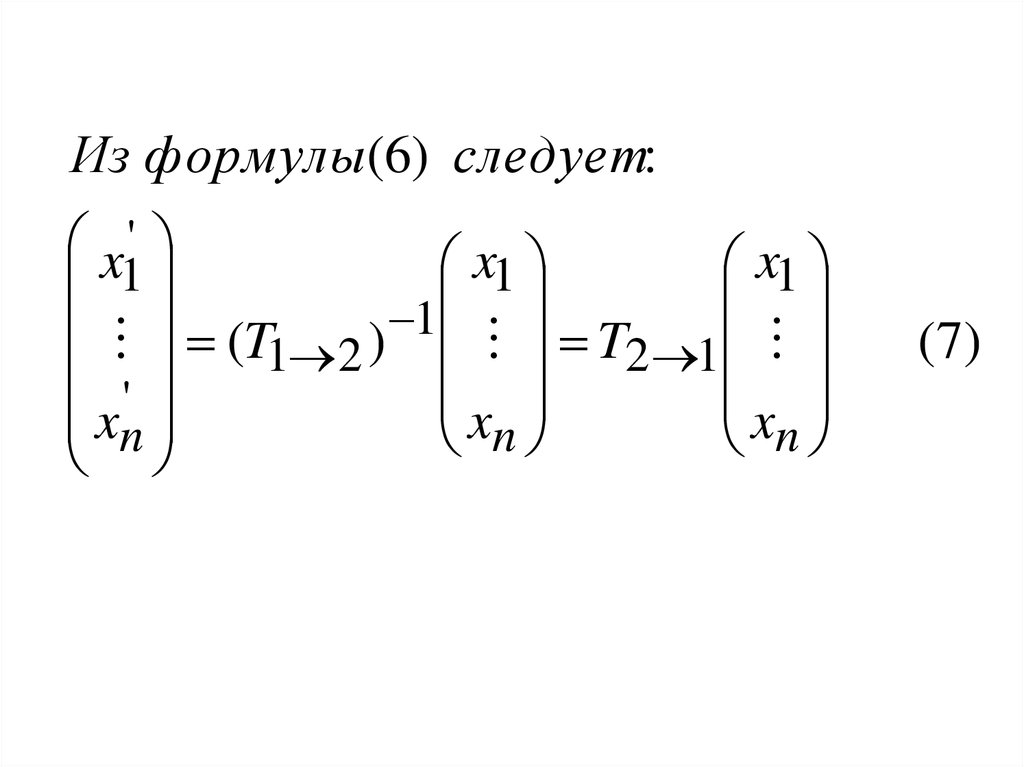





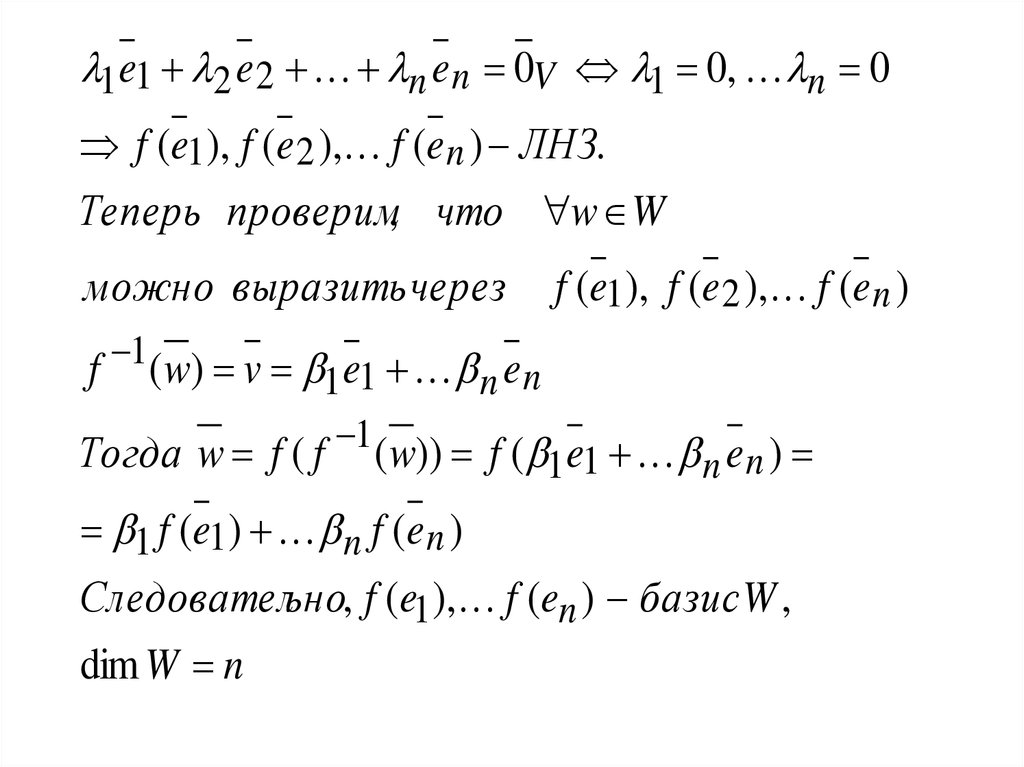



 mathematics
mathematics








