Линейные пространства. Нормированные пространства. Подпространства

1.

ЛИНЕЙНЫЕ ПРОСТРАНСТВА
Множество E называется линейным пространством (ЛП) над полем
ли в нем определены две операции:
1) x, y E определен элемент x y E – сумма;
2) x E определен элемент x E
так, что выполнены аксиомы x, y, z E , :
1) x y y x ;
2) x y z x y z ;
3) 0 E такой, что x 0 x ;
4) x x ;
5) 1 x x и 0 x 0 , где 0,1 ;
6) x y x y ;
, ес-
7) x x x .
Замечание.
не обязательно числовое множество. Пространства над вещественным или комплексным полем, обычно называют вещественным или комплексным ЛП.
1

2.

n
Пусть k k . Тогда k xk – линейная комбинация элементов
k 1
x1 , x2 ,..., xn E .
Элементы x1 , x2 ,..., xn линейно зависимыми, если существует их лиn
n
k 1
k 1
нейная комбинация k xk 0 , где k 0 .
ЛП называется m -мерным, если в нем существует m линейно независимых векторов, а всякие m 1 векторов линейно зависимы.
Набор любых m линейно независимых векторов в m -мерном линейном
пространстве E называется базисом в E .
m
Если ek k 1 произвольный базис в E , то x E существуют скаляры
m
1 , 2 ,..., m такие, что x k ek .
k 1
ЛП E называется бесконечномерным, если для каждого натурального
n в E существует n линейно независимых элементов.
2

3.

НОРМИРОВАННЫЕ ПРОСТРАНСТВА
ЛП E называется нормированным (ЛНП), если x E поставлено в соответствие неотрицательное число x так, что выполнены следующие 4 аксиомы:
1) Неотрицательность: x E x 0 .
2) Однородность:
x x .
3) Неравенство треугольника: x, y E x y x y .
4) Невырожденность: x 0 x 0 .
Следствия:
1) 0 0 . 0 0 x 0 x 0 .
2) Обратное неравенство треугольника: x y x y .
x x y y x y y , x y x y ,
x y x y
y
x
y
x
.
y y x x y x x .
З а м е ч а н и е . Если выполняются аксиомы 1)-3), а 4)-я аксиома не выполняется, то
говорят, что задана полунорма.
Например, в пространстве интегрируемых на сегменте a, b функция
b
x f x dx является полунормой. Однако если функции, для которых f g 0
a
считать равными, то функция станет нормой.
3

4.

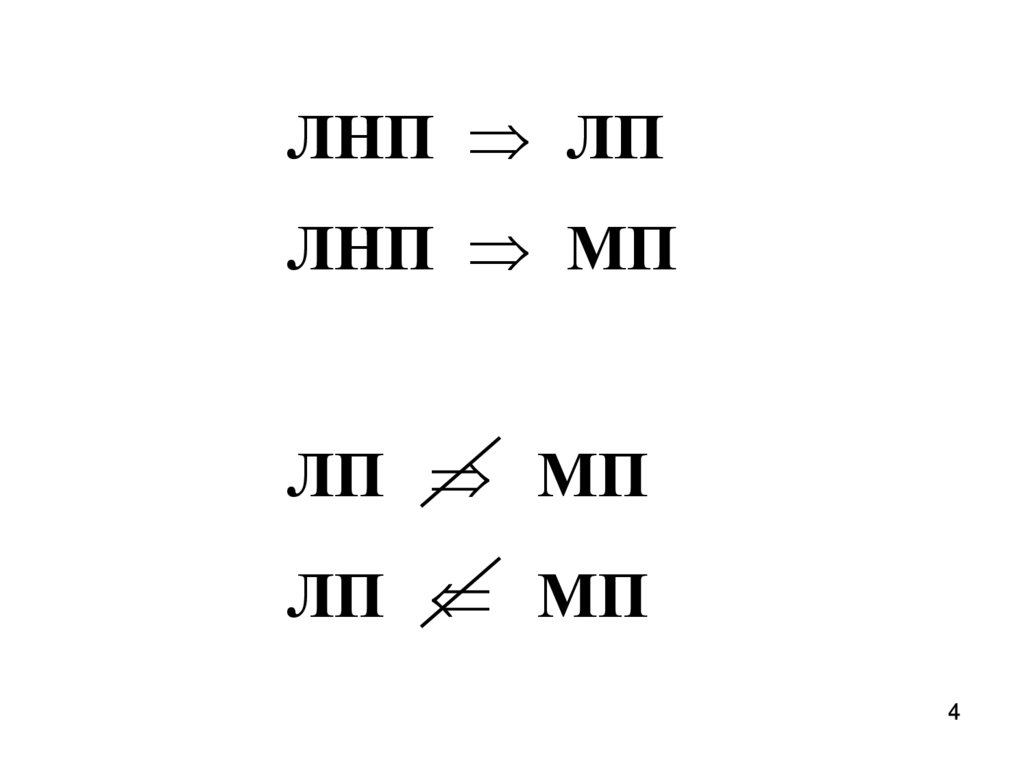
ЛНП ЛП
ЛНП МП
ЛП МП
ЛП МП
4

5.

Норма x 2 в ЛНП X подчиненна норме x 1 , если
c , c 0, x X x 2 c x 1 .
Две нормы x 1 и x 2 в ЛНП X эквивалентны, если существуют
такие постоянные c1 0 и c2 0 , что
x X c1 x 1 x 2 c2 x 1 .
Если норма x 2 подчинена норме x 1 и
– xn сходится к x0 по норме x 1 , то сходится и по норме x 2 ,
– xn расходится по норме x 2 , то она расходится и по норме x 1 .
Если нормы x 1 , x 2 эквивалентны, то последовательность либо в
обеих нормах сходится, либо в обеих нормах расходится.
5

6.

Норма x 2 в ЛНП X подчиненна норме x 1 , если
c , c 0, x X x 2 c x 1 .
1. Пусть xn сходится к x0 по норме x 1 , тогда
0 n0 n n0 xn x0 1
Следовательно,
0 n0 n n0 xn x0 2 c xn x0 1 c ,
т.е. xn сходится и по норме x 2 ,
2. Пусть xn расходится по норме x 2 , тогда
0 n0 n n0 xn x0 2
Следовательно,
0 n0 n n0 xn x0 1
т.е. xn расходится и по норме x 1 .
1
xn x0 2 .
c
c
6

7.

1. В конечномерных пространствах все нормы эквивалентны.
2. Норма x A подчинена норме x B , т.е. c 0 x A c x B .
xB
x A
Последовательности
sup xi
p
i
p q
xi
xi , p 1
p
i 1
p q
, q 0
p
i 1
xi
p
i 1
Функции
f x dx , p 1
sup f x
f x dx
p q
p
p
x
p
p
p q
f x
dx , q 0
7

8.

Связь между сходимостью в бесконечномерных пространствах
"Сходится в B" "Сходится в A"
A
B
Последовательности
c0
c, m
c
m
lp , p 1
c0 , c , m , l p q , q 0
Функции
C k m , k , m
C
C k , C , M ,
CLp , Lp , p 1
M ,
CLp , Lp , p 1
CLp , p 1
CLp q , Lp q , q 0
Lp , p 1
Lp q , q 0
10

9.

Фундаментальные и сходящиеся последовательности
Последовательность xn элементов МП X называется сходящейся в себе
(или фундаментальной, или последовательностью Коши), если
:
0 n0 n, m n0 xn , xm
или 0 n0 n n0 k xn k , xn
В ЛНП последовательность xn называется фундаментальной относительно нормы пространства, если она фундаментальна относительно метрики, порожденной этой нормой ( X x, y x y X ), т.е.
0 n0 n, m n0 xn xm
или 0 n0 n n0 k xn k xn
11

10.

МП X называется полным, если в нем всякая ФП сходится.
ЛНП называется полным, если оно является полным в смысле метрики,
порождаемой нормой данного пространства. Полное ЛНП называется банаховым (или B -пространством).
Если X полное пространство, то
« xn сходится» « xn фундаментальна»
« xn не фундаментальна» « xn рассходится»
Если X не является полным пространством, то
« xn сходится» « xn фундаментальна»
« xn не фундаментальна» « xn расходится»
« xn сходится» « xn фундаментальна»
« xn не фундаментальна» « xn расходится»
14

11.

Примеры банаховых (полных) пространств
1. Все конечномерные пространства
2. Пространства последовательностей: c0 , c , l p , l m .
3. Пространства функций: M , C , L p .
З а м е ч а н и е : Пространства C k и CLp не являются
банаховыми (полными).
15

12.

Теорема о вложенных шарах. Пусть в полном МП X дана последовательность замкнутых шаров D n an , n 1, 2,... , вложенных друг в друга, радиусы
которых стремятся к нулю, т.е.
m n D m am D n an и lim n 0 .
Тогда ! a X n
n
a D n an .
Существование. При m n am D m am D n an an , am n
an – ФП.
X полное
a X a lim an .
Радиусы шаров стремятся к нулю и n, p
n
an p D n an
an p a при p .
Шары замкнуты, поэтому n
a D n an .
Единственность. От противного. Пусть существует b a , принадлежащая
всем шарам, тогда
a, b 0 и a, b a, an an , b 2 n 0 ,
что невозможно.
16

13.

Подпространства
1. Подпространством МП X – называют множество Y X , имеющее ту
же метрику, что и X .
2. Подпространством ЛП X называют множество Y X , являющееся ЛП
с теми же операциями, что и X .
Множество L в ЛП X называется линейным многообразием (линейным
множеством), если x, y L и любых скаляров , x y L .
Лемма. Всякое линейное многообразие в ЛП X является ЛП с теми же операциями, что и X , а значит, всякое линейное многообразие L в ЛП X является
подпространством ЛП X .
3. Подпространством ЛНП X – называют замкнутое множество Y X ,
имеющее ту же норму и те же операции, что и пространство X .
Лемма. В конечномерном ЛНП всякое линейное многообразие является
подпространством. В бесконечномерном случае это не так (например, в пространстве C a, b многочлены образуют линейное многообразие, но не подпространство (так как не замкнуто).
17

14.

Всякое линейное многообразие в конечномерном ЛНП
есть подпространство.
Всякое конечномерное линейное многообразие в ЛНП
есть подпространство.
В
ЛНП
замыкание
есть подпространство.
линейного
многообразия
Примеры подпространств ЛНП:
1) с0 – подпространство с ;
2) с – подпространство m ;
3) пространство всех многочленов степени k –
подпространство C a, b .
18

15.

Линейные многообразия плотные в ЛНП
Линейное многообразие L E , называется плотным в ЛНП E , если
x E 0 u L x u ,
З а м е ч а н и е . Если L плотно в E , то
1) L E ,
2) x E последовательность un такая, что un L , lim un x .
n
Теоремы Вейерштрасса:
n
1. Линейное многообразие всех полиномов ak t k плотно в C a, b .
k 0
2. Линейное многообразие всех тригонометрических многочленов
a0 n
ak cos kx bk sin kx
2 k 1
плотно в ЛНП непрерывных на , функций, удовлетворяющих граничному условию f f , с нормой f max f t .
t ,
19

16.

Теорема о пополнении метрических пространств
Любое МП X можно пополнить, точнее: оно всегда может быть вложено
в другое полное метрическое пространство X такое, что в нем существует
всюду плотное в X подпространство X 0 , изометричное пространству X .
Пространство X называют пополнением или замыканием пространства X .
Теорема о пополнении ЛНП
Всякое ЛНП E можно рассматривать как линейное многообразие, плотное в некотором банаховом пространстве Ê Пространство Ê называют
пополнением пространства E .
20

17.

Построение для произвольного ЛНП E пополнения Ê
Рассмотрим всевозможные ФП xn пространства E .
Если xn xn 0 , n , то последовательности xn и xn будем называть
эквивалентными (и писать xn
xn ).
Множество всех ФП разобьем на классы эквивалентности:
две последовательности xn и xn включаем в один класс тогда и только
тогда, когда xn
xn ).
Классы обозначим через xˆ, yˆ ,... Если xn xˆ , то xn – представитель класса x̂ .
Элементами пространства Ê будут классы эквивалентности фундаментальных в
E последовательностей.
21

18.

Операции сложения и умножения в Ê
– xˆ yˆ – класс, содержащий xn yn , где xn xˆ и yn yˆ .
– x̂ – класс, содержащий xn , где xn xˆ .
З а м е ч а н и е 1 . Определение классов xˆ yˆ , x̂ не зависит от выбора представителей классов.
xn xˆ
xn yn xn yn xn yn xˆ yˆ ;
yn yˆ
Для класса x̂ аналогично.
З а м е ч а н и е 2 . Классы xn yn , xn состоят из ФП.
Нуль в Ê – класс 0 , представителем которого является 0 E .
Норма в Ê : xˆ Eˆ lim xn E , где xn xˆ .
n
З а м е ч а н и е 1 . Предел существует, т.к. xn – числовая ФП:
xn xm
xn xm .
З а м е ч а н и е 2 . Предел не зависит от выбора представителей класса x̂ :
Если также xn xˆ , то xn xn xn xn 0 , n . 22