Similar presentations:
Пространство в современной физике
1. Пространство
Понятие пространства всовременной физике
2.
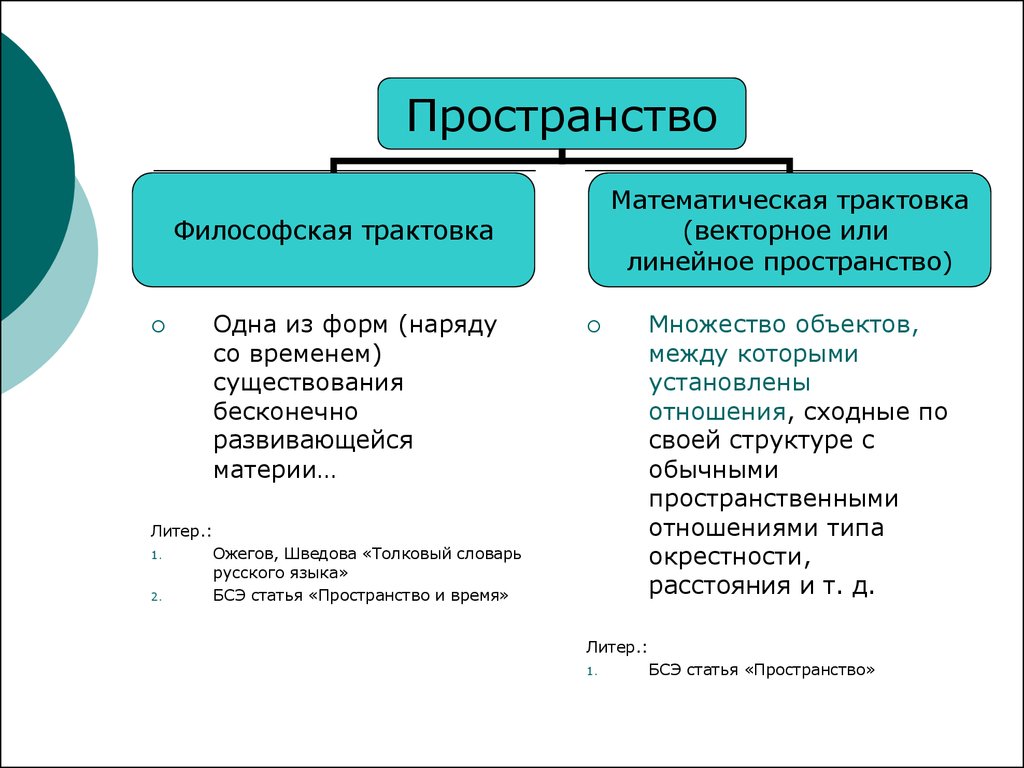
ПространствоМатематическая трактовка
(векторное или
линейное пространство)
Философская трактовка
Одна из форм (наряду
со временем)
существования
бесконечно
развивающейся
материи…
Литер.:
1.
2.
Ожегов, Шведова «Толковый словарь
русского языка»
БСЭ статья «Пространство и время»
Множество объектов,
между которыми
установлены
отношения, сходные по
своей структуре с
обычными
пространственными
отношениями типа
окрестности,
расстояния и т. д.
Литер.:
1.
БСЭ статья «Пространство»
3. Пространство в современной физике
В современной физикеиспользуется математическая
трактовка
4. Линейная алгебра: поле
Поле – множество элементов свведенными на нем операциями
«+» и «*»; при этом операции
«+» и «*» должны обладать
определенным набором свойств
5. Линейная алгебра: поле
Коммутативность:a b b a,
a b b a;
Ассоциативность:
a (b c) (a b) c,
a (b c) (a b) c;
Наличие нейтрального и обратного элемента:
a 0 a,
a ( a ) 0,
a 1 a;
1
a 1;
a
Дистрибутивность:
a (b c) a b a c.
6. Примеры полей
Рациональные, вещественныечисла
Не являются полями: целые
числа, натуральные числа
Будем говорить о поле
вещественных чисел
7. Векторное пространство
Пространство над полем P – этомножество элементов, на котором
введены операции сложения и
умножения на скаляр,
обладающие определенными
свойствами
Скаляр – элемент поля P
8. Векторное пространство
Элемент пространства – векторВектор задается координатами:
a (a1 , a2 ,..., an );
Радиус-вектор – вектор, начало
которого лежит в начале
координат
Координатами точки называются
координаты ее радиус-вектора
9. Размерность пространства
Рассмотрим линейную комбинацию:1 x1 2 x2 ... n xn ,
Где αn – ненулевые скаляры, а xn – произвольные векторы.
Попытаемся подобрать скаляры так, чтобы л. к.
обратилась в нуль. Размерность пространства максимальное число векторов, для которых
этого сделать не удастся. А оставшийся набор
векторов называется базисом
Можно показать, что размерность пространство
совпадает с числом координат векторов
Вещественное пространство размерности n
обозначается Rn
10. Евклидово пространство
Пространство, свойства которогоизучаются в евклидовой
геометрии. В более широком
понимании Е. п. называют nмерное векторное пространство, в
котором определено скалярное
произведенье
Литер.:
1.
БСЭ статья «Евклидово пространство»
11. Евклидово пространство: скалярное произведенье
Рассмотрим:x ( x1 , x2 ),
y ( y1 , y2 ),
Где x, y принадлежат пространству R2, а x1, x2, y1, y2 – полю
R.
Введем скалярное произведенье:
x y x1 y1 x2 y2 ,
Причем λ принадлежит полю P.
Скалярное произведенье порождает норму:
x x x x x .
2
1
2
2
12. Евклидово пространство
Наше пространство – трехмерноеевклидово пространство
13. Аксиомы Евклида
5 постулатов, на которых строитсягеометрия евклидового
пространства
Сформулированы Евклидом для R2
Гильберт уточнил аксиоматику и
распространил ее на случай R3
14. Фазовое пространство
Рассмотрим систему из N молекул. В каждыймомент времени у каждой i-той молекулы
определен вектор скорости:
vi (vi ,1 , vi , 2 , vi , 3 ),
и радиус-вектор (вектор-положение):
ri (ri ,1 , ri , 2 , ri , 3 ).
В каждый момент времени состояние системы
описывается точкой в 6N-мерном фазовом
пространстве:
( x1,1 , x1, 2 , x1, 3 , x2,1 ,..., xN ,1 , xN , 2 , xN , 3 , v1,1 , v1, 2 , v1, 3 , v2,1 ,..., vN ,1 , vN , 2 , vN , 3 ).
15. Пространство Минковского
Четырехмерное пространство.Помимо пространственных
координат вводится временная ct
Не является Евклидовым, так как
определение нормы отлично от
данного выше
Квадрат нормы в пространстве
Минковского:
s 2 c 2 (t1 t2 ) 2 ( x1 x2 ) 2 ( y1 y2 ) 2 ( y1 y2 ) 2
16. Пространство Минковского
Пространство Минковского можносделать евклидовым, введя
евклидову норму, но, зачастую,
это неудобно
17. Пятый постулат Евклида
Через точку, не лежащую наданной прямой, проходит только
одна прямая, лежащая с данной
прямой в одной плоскости и не
пересекающая её
18. Геометрия Лобачевского
Через точку, не лежащую наданной прямой, проходят по
крайней мере две прямые,
лежащие с данной прямой в одной
плоскости и не пересекающие её
19. Геометрия Лобачевского
Лобачевскому удалось на основесвоей аксиоматики построить
полную и непротиворечивую
геометрию
Геометрия Лобачевского находит
применение в специальной и
общей теории относительности
20. Выводы
Понятие пространства в физике – этоабсолютно строгая математическая
модель
Евклидово пространство – частный
случай этой модели
В большинстве случаев удобно
полагать, что мы живем в трехмерном
Евклидовом пространстве
Часто для расчета физических
процессов приходится прибегать к
использованию евклидовых пространств
с большим числом измерений
21. Список литературы
1.2.
3.
4.
5.
Ильин В. А., Позняк Э.Г. «Линейная алгебра». Изд.: Москва
Наука 1999 г.
Гельфанд И. М. «Лекции по линейной алгебре». Изд.:
МЦНМО 1998 г.
Апатенок Р. Ф. «Элементы линейной алгебры». Изд.: Минск
«Высшая школа» 1977 г.
Н. В. Ефимов, Э. Р. Розендорн. «Линейная алгебра и
многомерная геометрия». 1970 г.
Манин Ю. И., Кострикин А. И. «Линейная алгебра и
геометрия». 1980 г.




















 mathematics
mathematics physics
physics








