Similar presentations:
Векторная алгебра. Вектор - направленный отрезок
1. Векторная алгебра
ВЕКТОРНАЯ АЛГЕБРАВектор – направленный отрезок.
а
1
2.
АВ аА
В
Модуль вектора –
длина направленного отрезка АВ a .
Векторы, которые лежат на одной прямой
или на параллельных прямых называются
коллинеарными.
Векторы, лежащие
в одной или параллельных плоскостях
называются компланарными.
2
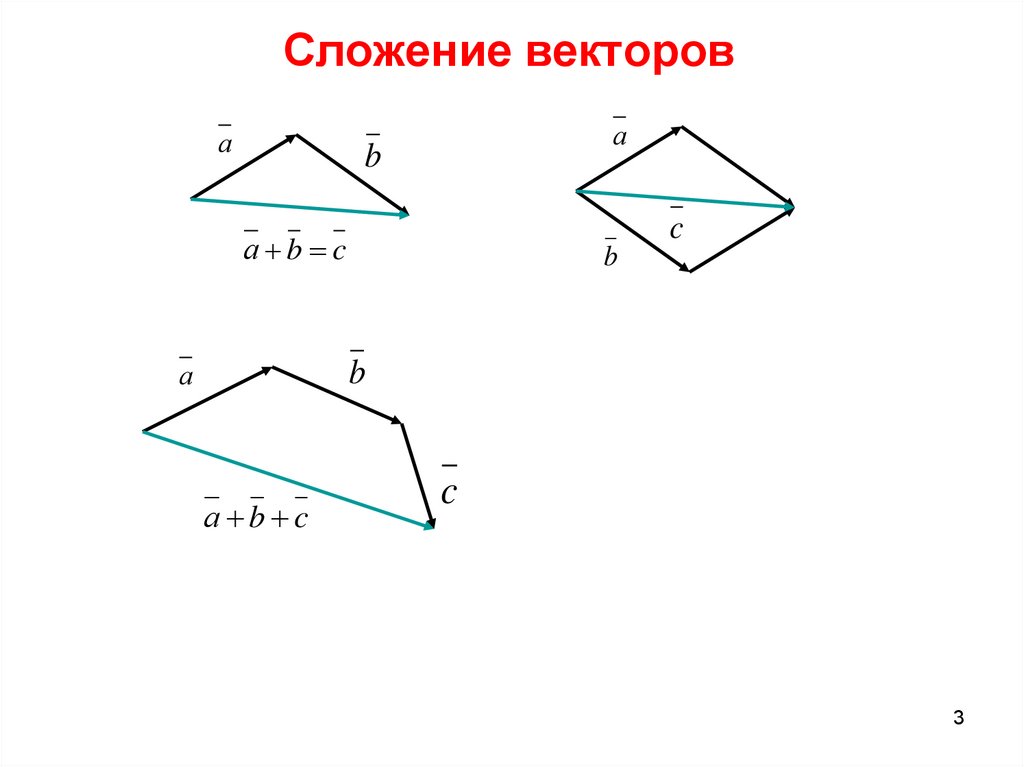
3. Сложение векторов
аа
b
c
а b c
а
b
b
а b c
c
3
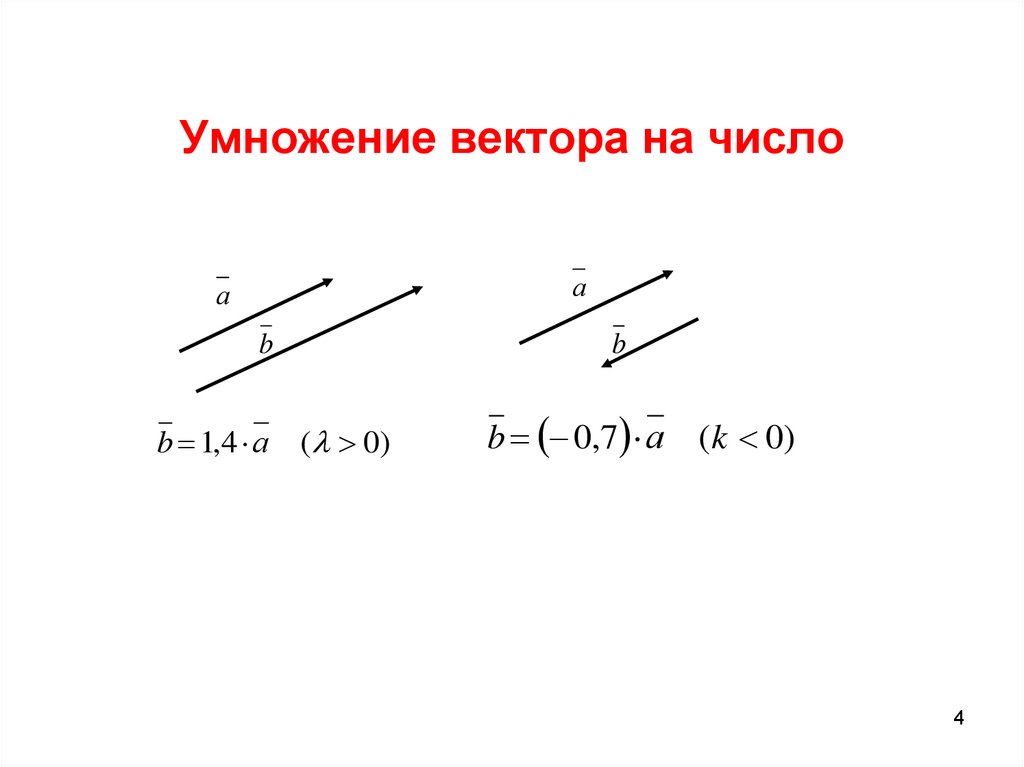
4. Умножение вектора на число
аа
b
b 1,4 а ( 0)
b
b 0,7 а (k 0)
4
5.
Множество всех векторов на плоскости, вкотором определены операции сложения
векторов и умножения на число называется
векторным пространством R2.
Множество всех векторов в пространстве, в
котором определены операции сложения
векторов и умножения на число называется
векторным пространством R3.
5
6. Проекция вектора на ось
BA
A1
B
A
B1
L
B1
A1
L
Проекцией вектора АВ на ось L пр L АВ
называется длина вектора А1В1, взятая со
знаком «+», если направление вектора А1В1
совпадает с осью L, и со знаком «-», если
направление А1В1 противоположно оси L.
прL AB AB cos
6
7. Ортонормированный базис в пространстве R3. Декартовы прямоугольные координаты.
zMz
M
k
i
x
Mx
j
0
М - точка в пространстве.
Проекции вектора ОМ на координатные
оси ОX, OY, OZ называются
координатами точки М
y и обозначаются М(x, y, z).
My Координаты радиус-вектора ОМ
равны координатам точки М.
OM x, y, z .
OM x 2 y 2 z 2
i, j , k базис в пространстве R 3 , длина базисных векторов равна 1.
OM OM x OM y OM z
OM x i y j z k
7
8.
Координаты вектора, заданногокоординатами начала и конца
М1 x1; y1; z1
z
M2
M1
М 2 x2 ; y2 ; z2
OM 1 M 1M 2 OM 2
OM 1 x1 i y1 j z1 k ,
0
x
y
OM 2 x2 i y2 j z 2 k .
M 1M 2 ( x2 x1 )i ( y2 y1 ) j ( z 2 z1 )k ,
M 1M 2 x2 x1 , y2 y1 , z 2 z1 .
Расстояние d между двумя точками:
d ( x 2 x1 ) 2 ( y 2 y1 ) 2 ( z 2 z1 ) 2 .
8
9. Линейные операции над векторами в координатной форме
a a x , a y , a z , b bx , b y , bz .a b ax bx , a y by , az bz
b a, b ax , a y , az
Следствие.
Координаты коллинеарных векторов пропорциональны.
by
bx
bz
k
ax
ay
az
9
10.
Деление отрезка в заданном отношенииМ 2 x2 ; y2 ; z2
M 1M
M 2M
М x; y; z
М1 x1; y1; z1
x x1 ( x2 x)
x x1 x2 x
x 1 x1 x2
M 1M MM 2
M 1M ( x x1 ); ( y y1 ); ( z z1 )
MM 2 ( x2 x); ( y2 y ); ( z2 z )
x1 x2
x
,
1
y1 y2
y
,
1
z1 z 2
z
.
1
Следствие.
Координаты
середины отрезка:
x1 x2 y1 y2 z1 z 2
;
;
2
2
2
10
11. Скалярное произведение векторов
aa b a b cos .
b
Условие перпендикулярности векторов a b a b 0.
11
12.
Формула скалярного произведенияв координатной форме
a a x , a y , a z , b bx , b y , bz ,
a b a x bx a y b y a z b z .
Задача.
Даны вершины четырехугольника А(1; 2; 3), В(7; 3; 2), C(-3; 0; 6), D(9; 2; 4).
1) Найти величину внутреннего угла при вершине С.
2) Доказать, что диагонали перпендикулярны.
1) CB 10;3; 4
2) AC 4; 2;3
CD 12;2; 2
CB CD CB CD cos C
cos C
CB CD
CB CD
C arccos 0,9721
BD 2; 1;2
AC BD 0 AC BD
134
0,9721
125 152
12
13.
Векторное пространство Rn, в котором определеноскалярное произведение называется Евклидовым
пространством и обозначается En .
13
14. Векторное произведение векторов
Векторным произведением векторов а и b называетсявектор с , определяемый условиями:
1) c a , c b ,
с
2) векторы a, b, c образуют правую тройку.
b
3) c a b sin S пар. ,
а
Если векторы заданы координатами, то координаты
векторного произведения вычисляются по формуле:
a y
a b
by
az ax
;
bz bx
az ax
;
bz bx
a y
.
by
14
15.
Задача.Найти площадь треугольника с вершинами А(1; 2; 0), В(3; 0; -3), С(5; 2; 6).
1
S ABC AB AC
2
AB 2; 2; 3
AC 4; 0; 6
2 3 2 3 2 2
AB AC
;
;
.
6 4 6 4 0
0
AB AC 12; 24;8
1
1
S ABC AB AC
144 576 64
2
2
1
784 14 кв.ед.
2
15
16. Смешанное произведение векторов
Смешанным произведением трёх векторов называетсяa b c (a b) c a (b c ).
Свойства:
а) Модуль смешанного произведения численно
равен объёму параллелепипеда, построенного
на перемножаемых векторах.
с
b
a
б) Необходимым и достаточным условием
компланарности трёх векторов является
равенство нулю их смешанного произведения.
Если векторы заданы своими координатами, то их смешанное произведение
вычисляется по формуле:
ax a y az
a b с bx by bz .
сx с y сz
16
17. Линейная зависимость векторов. Базис векторного пространства.
Векторы a1 , a2 , , ak называются линейно-зависимыми,если существуют числа 1 , 2 , , k , из которых хотя бы
одно отлично от нуля, такие, что 1 a1 2 a2 k ak 0.
В противном случае векторы называются линейнонезависимыми.
Совокупность n линейно-независимых векторов в
пространстве Rn называется базисом.
Теорема. Любой вектор пространства Rn можно разложить
по базису единственным образом.
17
18.
Задача. Доказать, что векторы a 2i j 2k , b i 2 j 3k , c 3i 4 j 7kкомпланарны.
2 1 2
a b с 1 2 3 28 8 9 12 24 7 29 29 0
3 4 7
18
















 mathematics
mathematics








