Векторная алгебра (лекция 4)

1.

2.

План.
1. Основные понятия.
2. Линейные операции над векторами.
3. Решение типовых задач.

3.

Вектор –это направленный отрезок.
Обозначается: a ; AB
a
A
B

4.

Длиной или модулем вектора называется
расстояние между его началом и концом.
Обозначается:
a ; AB
Векторы, лежащие на одной прямой или
на параллельных прямых, называются
коллинеарными.
Если начало и конец вектора совпадают,
то вектор называется нулевым.

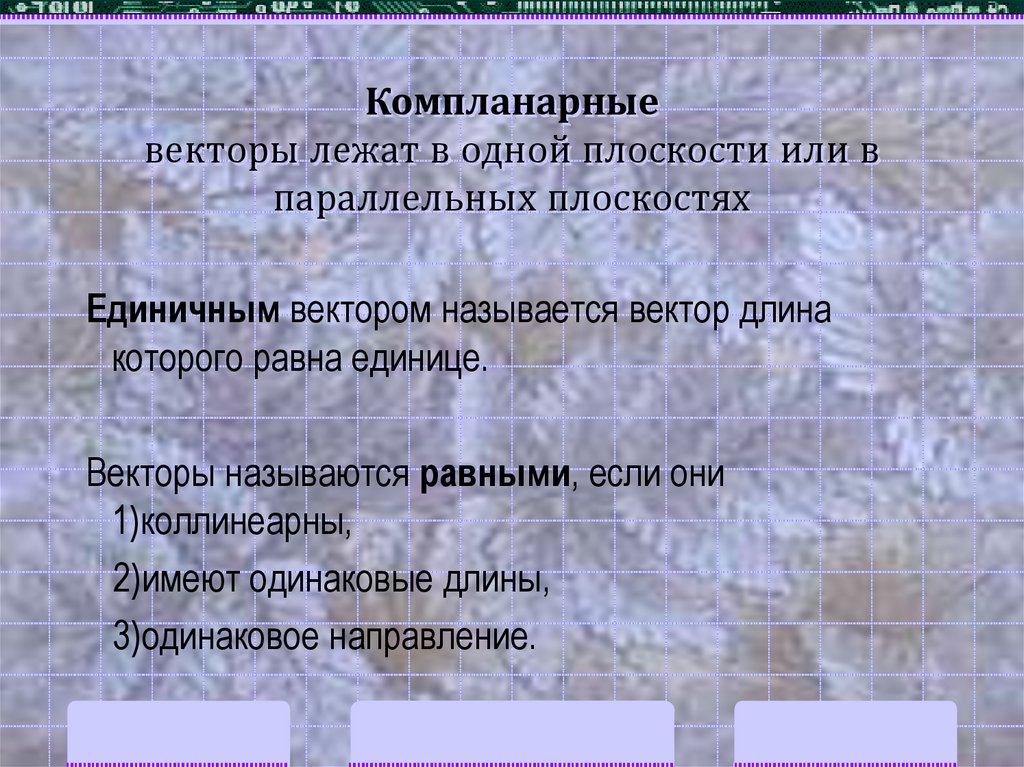
5. Компланарные векторы лежат в одной плоскости или в параллельных плоскостях

Единичным вектором называется вектор длина
которого равна единице.
Векторы называются равными, если они
1)коллинеарны,
2)имеют одинаковые длины,
3)одинаковое направление.

6.

В любой системе отсчета вектор характеризуется
своими координатами.
Пусть в системе отсчета XYZ заданы координаты
начала и конца вектора:
A( x1 , y1 , z1 ) B( x2 , y2 , z2 )
Тогда координаты вектора будут:
AB ( x2 x1; y2 y1; z2 z1 )
Где:
x x2 x1 Или:
y y2 y1
z z2 z1
AB x i y j z k

7.

z
B
z2
A
z1
i
x1
x2
x
k
j
y1
y2
y

8.

Длина вектора определяется по формуле:
AB ( x2 x1 ) ( y2 y1 ) ( z2 z1 )
2
2
x y z
2
2
2
2

9.

Пусть два вектора заданы своими координатами:
a (a1 , a2 , a3 ) b (b1 , b2 , b3 )
Если
эти
вектора
коллинеарны,
то
их
соответствующие
координаты
должны
быть
пропорциональны:
a1 a2 a3
b1 b2 b3

10. 2. Линейными операциями над векторами называются сложение векторов и умножение вектора на число.

1.Сложение векторов: правило треугольника, правило
параллелограмма, сложение координат векторов.
2.Умножение вектора на действительное число: если число
положительное, то векторы направлены одинаково, если
число отрицательное, то векторы противоположны.

11.

Для построения суммы векторов, нужно совместить
конец первого вектора с началом второго. Тогда
вектор их суммы будет направлен от начала первого
вектора к концу второго:
b
a
c a b
Аналогично определяется сумма нескольких векторов.

12.

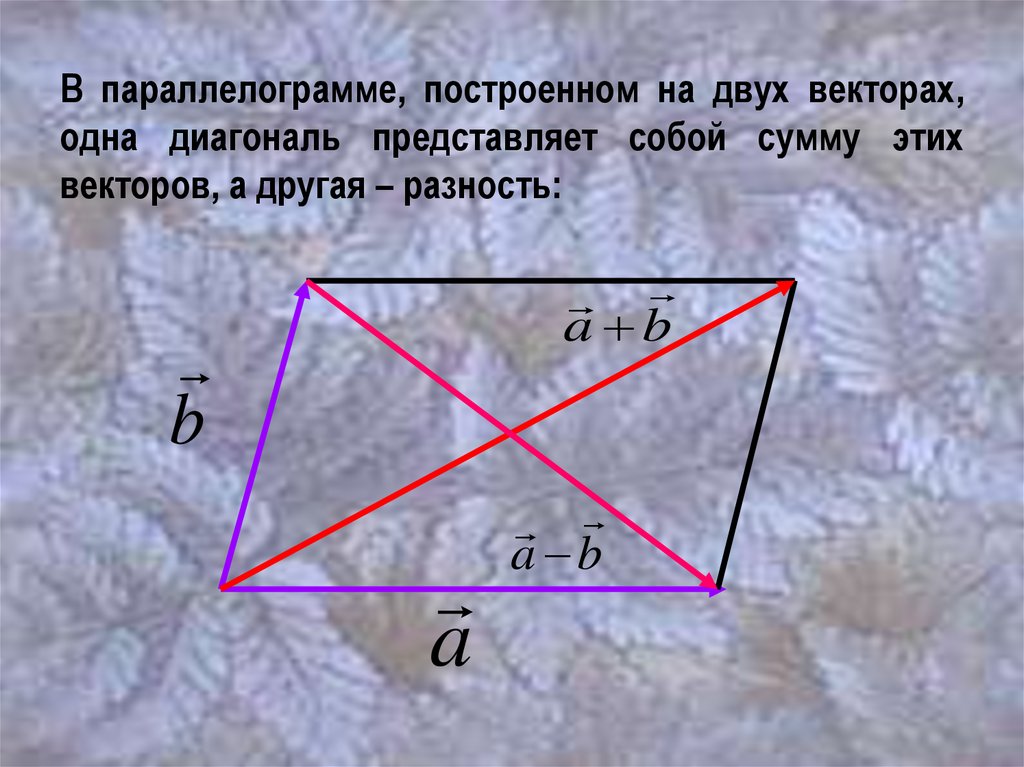
В параллелограмме, построенном на двух векторах,
одна диагональ представляет собой сумму этих
векторов, а другая – разность:
a b
b
a
a b

13.

Суммой двух векторов будет вектор,
координаты которого равны суммам
соответствующих координат исходных
векторов.
a (a1 , a2 , a3 ) b (b1 , b2 , b3 )
c a b
c (c1 , c2 , c3 )
c1 a1 b1 c2 a2 b2
c3 a3 b3

14.

Произведением вектора на число будет
вектор, координаты которого равны
произведению соответствующих
координат исходного вектора на это
число.
a (a1 , a2 , a3 )
a c
c1 a1
c (c1 , c2 , c3 )
c2 a2
c3 a3

15.

Геометрически смысл умножения вектора
на число заключается в увеличении его
длины в λ раз, если lλl>1, и в ее сокращении
во столько же раз при lλl<1.

16.

Скалярным произведением двух
векторов называется число, равное
произведению длин этих векторов на
косинус угла между ними.
(a, b ) a b cos a ; b

17.

Если два вектора заданы своими координатами:
a (a1 , a2 , a3 ) b (b1 , b2 , b3 )
То скалярное произведение выразится следующим
образом:
(a , b ) a1b1 a2b2 a3b3
Отсюда можно
векторами:
выразить
угол
(a , b )
cos a ; b
a b
между
двумя

18.

Если два вектора перпендикулярны, то их скалярное
произведение должно быть равно нулю:
(a, b ) a1b1 a2b2 a3b3 0

19. Векторное произведение векторов

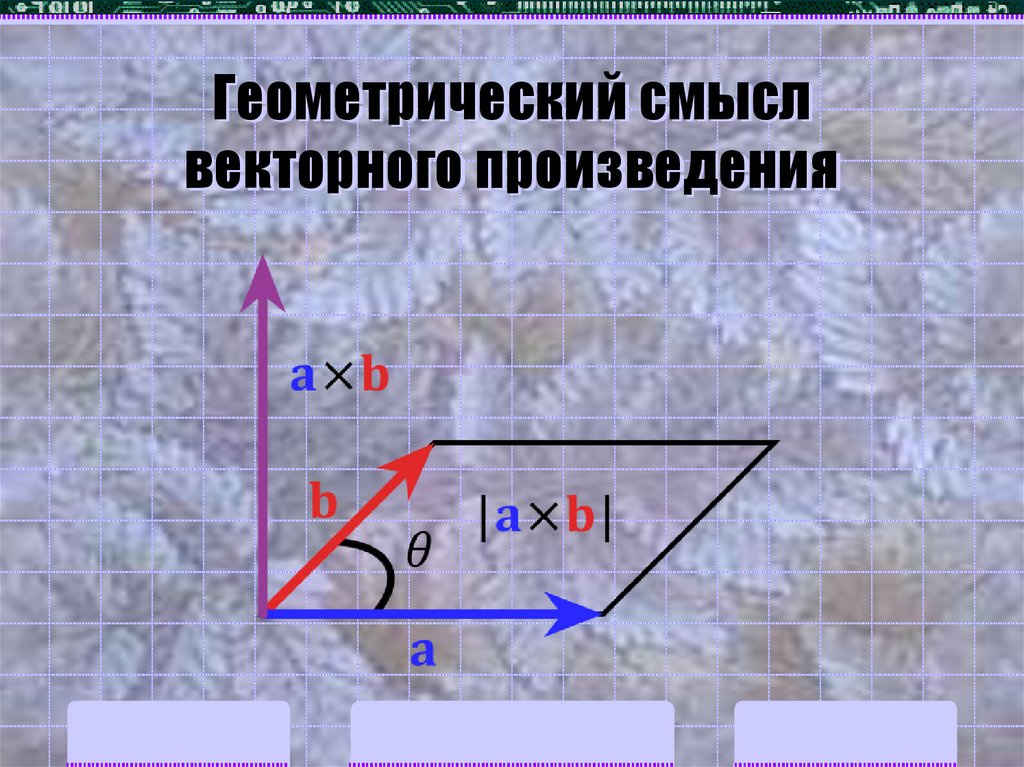
20. Геометрический смысл векторного произведения

21. Смешанным произведением трех векторов называется число, равное скалярному произведению вектора на вектор

с
Смешанным произведением трех векторов
называется число, равное скалярному произведению вектора
на вектор
с
a b

22. 3. Решение задач

Пример: Даны координаты вершин пирамиды АВСD: А
(0; 0; 1),В (2; 3; 5) С (6; 2; 3), D (3; 7; 2).
Найти: 1) записать векторы в системе орт и найти
модули этих векторов;
2) найти угол между векторами;
3)найти проекцию вектора на вектор ;
4) найти площадь грани АВС;
5)найти объем пирамиды АВСD.

23. Решение

1. Если М(х, у, z) и М(х, у, z), то:
M 1M 2 ( x2 x1 )i ( y2 y1 ) j ( z2 z1 )k
AB (2 0)i (3 0) j (5 1)k 2i 3 j 4k ;
AC (6 0)i (2 0) j (3 1)k 6i 2 j 2k ;
AD (3 0)i (7 0) j (2 1)k 3i 7 j k .

24. Модуль вектора

2
2
2
Модуль вектора a ax a y az
АВ 2 2 32 4 2 29
АС 6 2 2 2 2 2 2 11
АD 32 7 2 12 59.

25. 2. Угол между векторами

АВ АС
2 6 3 2 4 2
13
cos cos АВ, АС
0,7279
2 29 11
319
АВ АС

26. 3. Проекция вектора AD на вектор AB

пр
AB
AD
AB AD 2 3 3 7 4 1 31
5,76
29
29
AB

27. 4. Площадь грани АВС

5 6
4. Площадь грани АВС
1
S ABC
AB AC
2
i j k
AB AC 2 3 4 2i 20 j 14k
6 2 2
1
S ABC
2
2 20 7 5 6
2
2
2

28. 5. Обьем пирамиды

1
V
a b c
6
V
1
6
AB AC AD
2 3 4
AB AC AD 6 2 2 2 2 14 3 6 6 4 42 6 120
3 7 1
1
V 120 20
6