Similar presentations:
Глава 4. Векторная алгебра. §1. Векторы
1.
2. Глава 4. Векторная алгебра
3. § 1. Векторы
4.
Определение.Вектором называется направленный
отрезок.
5.
Вектор с началом А и концом Вобозначается AB (или AB); векторы
также обозначаются: a , b , c , ... (или
a, b , c , ...).
6.
Определение.Длиной (или модулем) вектора
называется расстояние между его
началом и концом.
Модули векторов AB и a
обозначаются AB и a
соответственно.
7.
Вектор нулевой длиныназывается нулевым вектором
(обозначается 0), вектор длины 1 –
единичным вектором (ортом).
8.
Векторы a и b называютсяколлинеарными векторами
(обозначаются a || b ), если они лежат
на одной прямой или на
параллельных прямых.
9.
Если a и b имеют одинаковоенаправление, то их называют
сонаправленными (обозначаются
a b ), а если противоположное –
противоположно направленными
(обозначаются a b ).
10.
Векторы называютсякомпланарными, если они
параллельны некоторой плоскости.
Векторы a и b называются
равными, если a b и a b .
11.
Из определения равенствавекторов следует, что начало
вектора можно помещать в любую
точку пространства. Такие векторы
называют свободными.
12.
Единичным вектором (илиортом) вектора a называется
вектор a0 такой, что a0 1 и
a
a0 a , причем a0 .
a
13.
Угол между векторами a, b(обозначается (a , b )) – наименьший
угол между направлениями векторов
a и b , 0 (a , b ) π.
14.
πЕсли (a , b ) , то векторы
2
называются ортогональными
(обозначаются a b ).
15.
К линейным операциям надвекторами относятся произведение
вектора на число и сумма векторов.
16.
Определение.Произведением вектора a на число λ
(λ R) называется вектор,
обозначаемый λa, такой, что:
17.
1) λa λ a ;2) λa a при λ > 0,
λa a при λ < 0,
λa 0 при λ 0 или a 0.
18.
Вектор a называетсяпротивоположным вектору a :
a 1 a.
19.
Определение.Суммой конечного числа векторов
расположенных так, что конец
каждого предыдущего вектора
является началом следующего,
называется замыкающий вектор,
направленный из начала первого
вектора в конец последнего.
20.
Правило треугольникаПравило параллелограмма
21.
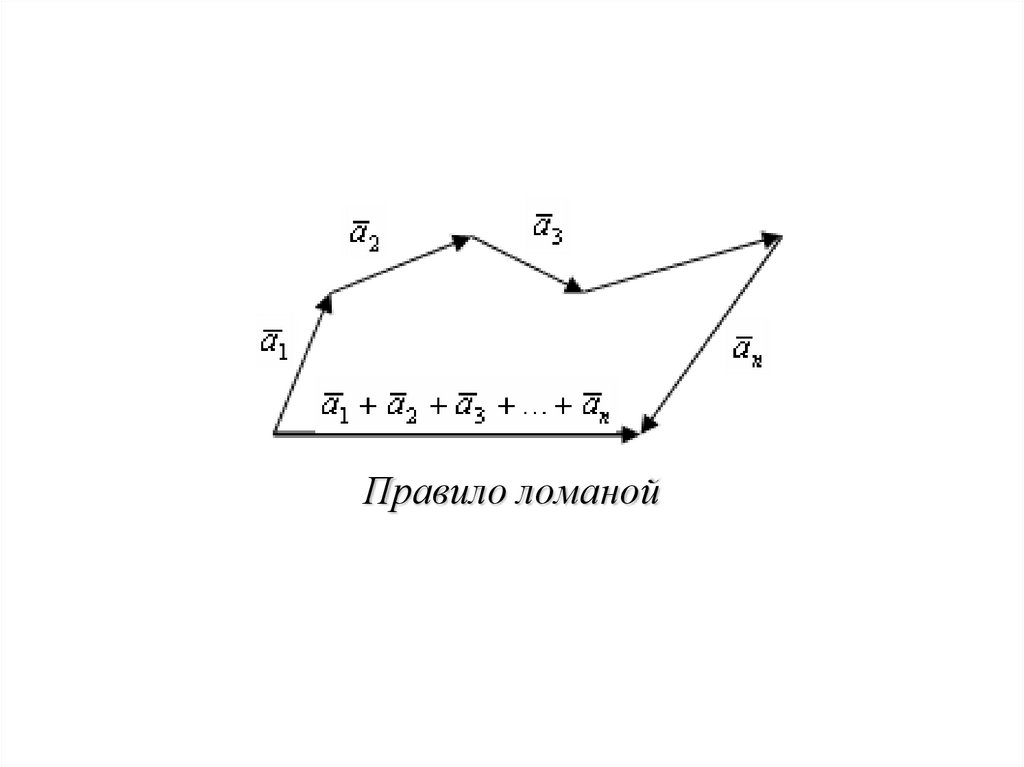
Правило ломаной22.
Правило параллелепипеда23.
Разностью векторов a и bназывается вектор a b a ( b ).
24.
Линейные операции надвекторами обладают свойствами:
1) a b b a;
2) (a b ) c a (b c );
3) a 0 a;
4) a ( a ) 0;
25.
5) λ(μa ) (λμ)a (λ, μ R);6) (λ μ)a λa μa (λ, μ R);
7) λ(a b ) λa λb (λ R);
8) 1 a a;
9) 0 a λ 0 0 (λ R).
26.
Осью называется прямая, накоторой задано положительное
направление.
27.
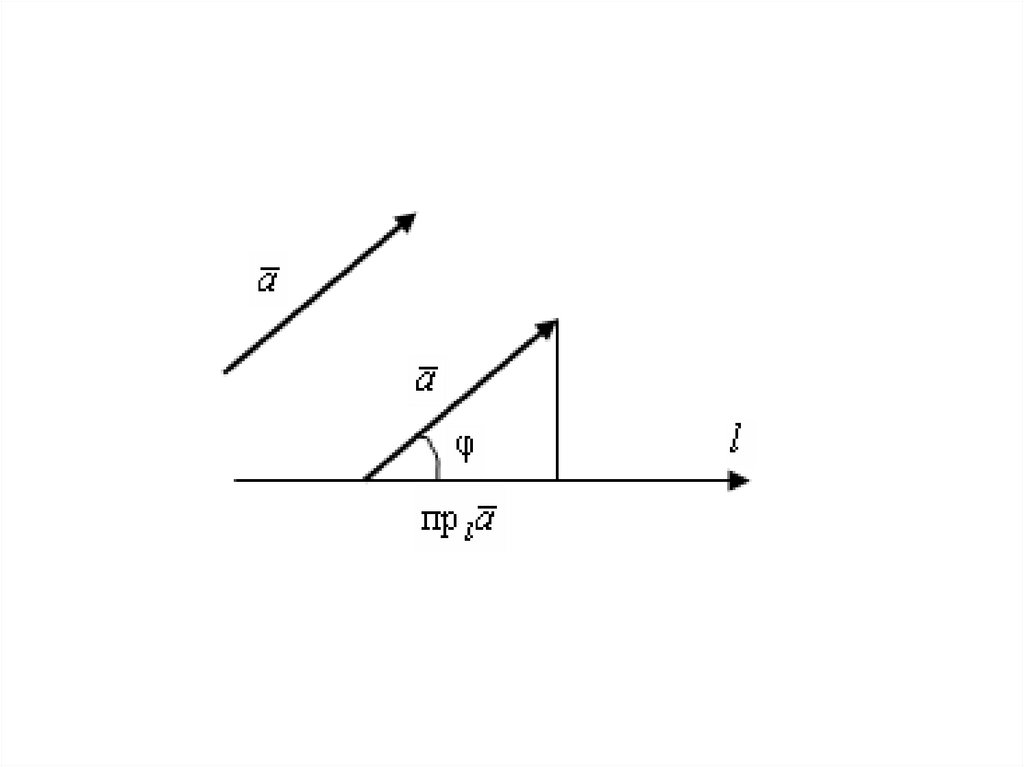
Определение.Проекцией вектора a на ось l
называется число
прl a a cos φ,
где φ (0 φ π) – угол между
положительным направлением оси l
и направлением вектора a.
28.
29.
Очевидно, чтоπ
прl a > 0 при 0 φ < ,
2
π
прl a 0 при φ ,
2
π
прl a < 0 при
< φ π.
2
30.
Проекция вектора на осьобладает свойствами:
1) прl (a b ) прl a прl b ;
2) прl (λa ) λпрl a (λ R);
3) если a b , то прl a прl b .
31.
Определение.Векторы a1, a2 , , an называются
линейно зависимыми, если
существуют числа λ1,λ 2 , ,λ n , не
все равные нулю, такие, что
λ1a1 λ2a2 ... λnan 0.
32.
В противном случае векторыa1, a2 , , an называются линейно
независимыми.
33.
Два коллинеарных векторалинейно зависимы, а два
неколлинеарных вектора на
плоскости линейно независимы.
34.
Три компланарных векторалинейно зависимы, а три
некомпланарных вектора в
пространстве линейно независимы.
35.
Определение.Базисом на плоскости называются
два упорядоченных неколлинеарных
вектора.
36.
Если {e1, e2} – базис в R2, толюбой вектор a плоскости можно
представить единственным образом
в виде линейной комбинации
a x1e1 x2e2 ,
37.
Числа x1, x2 называютсякоординатами вектора a в базисе
{e1, e2}; пишут: a ( x1, x2 ).
38.
Определение.Базисом в пространстве
называются три упорядоченных
некомпланарных вектора.
39.
Если {e1, e2 , e3} – базис в R3, толюбой вектор a пространства можно
представить единственным образом
в виде линейной комбинации
a x1e1 x2e2 x3e3 ,
40.
Числа x1, x2, x3 называютсякоординатами вектора a в базисе
{e1, e2 , e3}; пишут: a ( x1, x2 , x3 ).
41.
Базис называетсяортонормированным, если базисные
векторы попарно ортогональны и
имеют единичную длину.
42.
Координаты вектора вортонормированном базисе
называются прямоугольными
декартовыми координатами.
43.
44. § 2. Прямоугольная декартова система координат
Прямоугольнаядекартова
система
координат
45.
Декартовой системойкоординат на плоскости называется
совокупность фиксированной точки
O и некоторого базиса {e1, e2}.
46.
Определение.Прямоугольной декартовой
системой координат на плоскости
(обозначается Oxy) называется
декартова система координат на
плоскости с ортонормированным
базисом {i , j }, где
i (1, 0), j (0,1).
47.
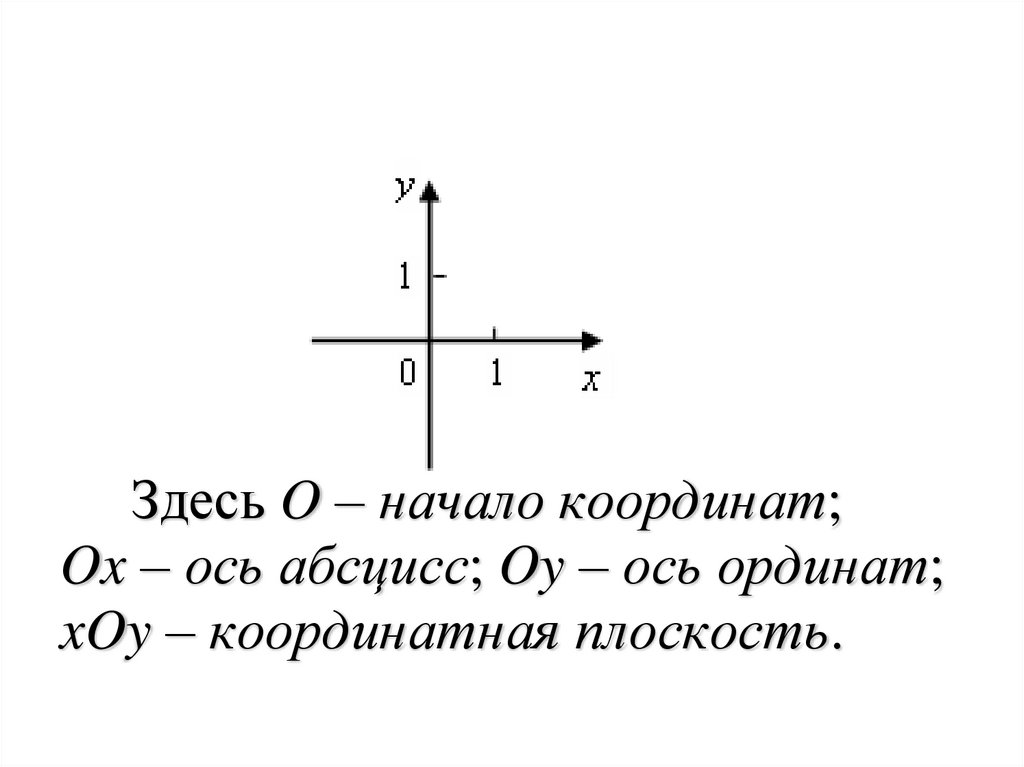
Здесь O – начало координат;Ox – ось абсцисс; Oy – ось ординат;
xOy – координатная плоскость.
48.
Декартовой системойкоординат в пространстве
называется совокупность
фиксированной точки O и
некоторого базиса {e1, e2 , e3}.
49.
Определение.Прямоугольной декартовой
системой координат в пространстве
(обозначается Oxyz) называется
декартова система координат в
пространстве с ортонормированным
базисом {i , j , k }, где
i (1, 0, 0), j (0,1, 0), k (0, 0,1).
50.
51.
Здесь O – начало координат;Ox – ось абсцисс; Oy – ось ординат;
Oz – ось аппликат; xOy, yOz, zOx –
координатные плоскости.
52.
Если a x1i y1 j z1k ,b x2i y2 j z2k , то:
λa λx1i λy1 j λz1k (λ R),
a b ( x1 x2 )i ( y1 y2 ) j ( z1 z2 )k .
53.
Теорема.Для коллинеарности ненулевых
векторов a и b необходимо и
достаточно, чтобы
x1 y1 z1
.
x2 y2 z2
54.
Радиус-вектор точки Mв рассматриваемой системе
координат – вектор OM .
Координатами точки M
называются координаты радиусавектора точки M.
55.
Если в прямоугольной системекоординат M1(x1; y1; z1) и
M2(x2; y2; z2), то:
M1M 2 ( x2 x1, y2 y1, z2 z1),
M1M 2 ( x2 x1 ) ( y2 y1 ) ( z2 z1) .
2
2
2
56.
Если отрезок M1M2 делитсяточкой M в отношении λ
(т.е. M1M λMM 2 ), где λ > 0, то
координаты точки M находятся по
формулам
y1 λy2
x1 λx2
z1 λz2
, z
x
, y
.
1 λ
1 λ
1 λ
57.
В частности, при λ 1 точка M –середина отрезка и
y1 y2
z1 z2
x1 x2
, z
.
x
, y
2
2
2
58.
Определение.Направляющими косинусами
вектора a xi yj zk называются
косинусы углов α, β, γ,
образованных вектором a с
положительными направлениями
осей Ox, Oy, Oz соответственно:
59.
xx
cosα
,
a
x2 y 2 z 2
y
y
cosβ
,
2
2
2
a
x y z
z
z
cos γ
.
a
x2 y 2 z 2
60.
Очевидно, чтоcos2α cos2β cos2γ 1.
Если a – единичный вектор, то
a (cosα, cosβ, cos γ).
61.
62. § 3. Скалярное произведение
63.
Определение.Скалярным произведением векторов
a и b (обозначается (a , b ), или a b
или ab ) называется число
(a , b ) a b cos(a, b ).
64.
Если a ( x1, y1, z1), b ( x2 , y2 , z2 )в базисе {i , j , k }, то
(a, b ) x1x2 y1 y2 z1z2.
65.
Число (a, a ) (a ) называетсяскалярным квадратом. Очевидно,
a (a, a ).
2
66.
Теорема.Для перпендикулярности ненулевых
векторов a и b необходимо и
достаточно, чтобы (a , b ) 0.
67.
Скалярное произведениевекторов обладает свойствами:
1) (a, b ) (b , a );
2) (a b , c ) (a, c ) (b , c );
3) (λa, b ) (a, λb ) λ(a, b ) (λ R);
4) (a, b ) a пр a b b пр b a.
68.
Рассмотрим приложенияскалярного произведения.
69.
Если a ( x1, y1, z1), b ( x2 , y2 , z2 )в базисе {i , j , k }, то:
x1x2 y1 y2 z1z2
(a , b )
cos(a , b )
,
a b
x12 y12 z12 x22 y22 z22
x1x2 y1 y2 z1z2
(
a
,
b
)
пр a b
.
a
x12 y12 z12
70.
Работа A силы F поперемещению материальной точки
на вектор s :
A ( F , s ) F s cos( F , s ).
71.
72. § 4. Векторное произведение
73.
Упорядоченная тройканекомпланарных векторов a, b , c
с общим началом называется
правой, если кратчайший поворот от
вектора a к вектору b наблюдается
из конца вектора c происходящим
против хода часовой стрелки.
74.
В противном случае тройкавекторов называется левой.
75.
Определение.Векторным произведением векторов
a и b (обозначается [a, b ] или a b )
называется вектор,
удовлетворяющий условиям:
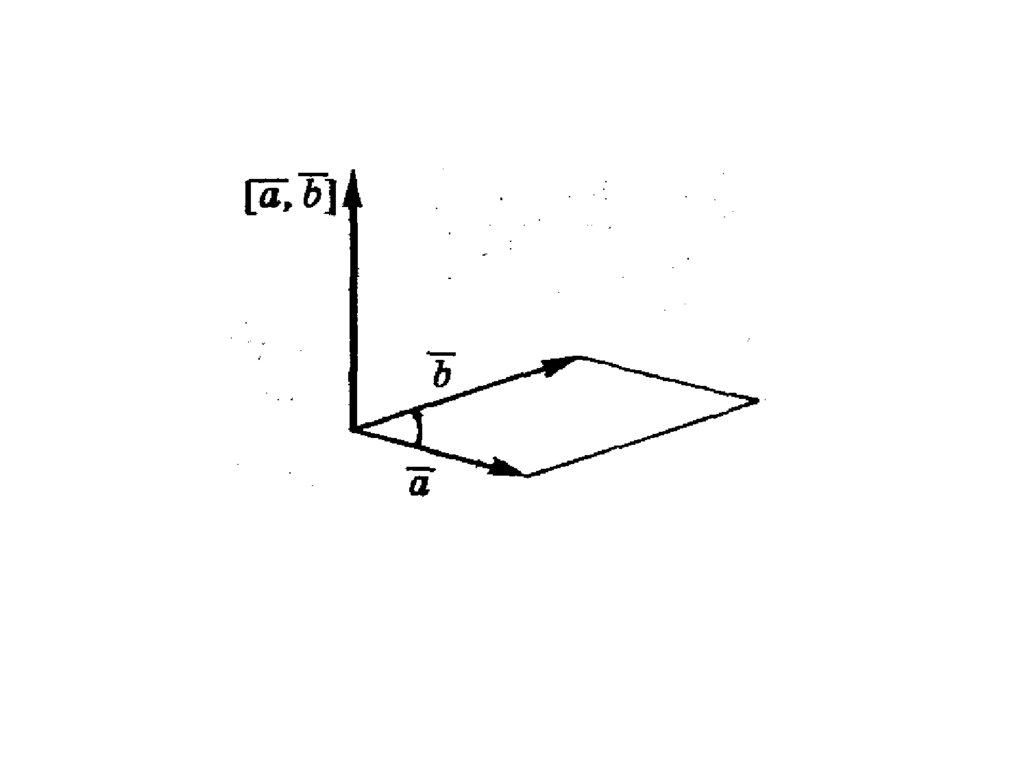
76.
1) [a , b ] a b sin (a , b );2) [a, b ] a и [a, b ] b ;
3) тройка векторов a , b , [a, b ] –
правая.
77.
78.
Если a ( x1, y1, z1), b ( x2 , y2 , z2 )в базисе {i , j , k }, то
i
j k
[a , b ] x1 y1 z1
x2 y2 z2
( y1z2 y2 z1)i ( x2 z1 x1z2 ) j ( x1 y2 x2 y1)k .
79.
Теорема.Для коллинеарности ненулевых
векторов a и b необходимо и
достаточно, чтобы [a, b ] 0.
80.
Векторное произведениевекторов обладает свойствами:
1) [a, b ] [b , a ];
2) [a b , c ] [a, c ] [b , c ];
3) [λa,b ] [a,λb ] λ[a,b ] (λ R).
81.
Рассмотрим приложениявекторного произведения.
82.
Площадь S параллелограмма,построенного на векторах a и b :
S [a , b ] .
83.
Площадь S треугольника,построенного на векторах a и b :
1
S [a , b ] .
2
84.
Вращающий момент M силы F ,приложенной в точке B тела,
закрепленного в точке A:
M [ AB, F ].
85.
86. § 5. Смешанное произведение
87.
Определение.Смешанным произведением
векторов a , b и c (обозначается
(a , b , c ) или abc ) называется число,
равное ([a, b ], c ).
88.
Если a ( x1, y1, z1), b ( x2 , y2 , z2 ),c ( x3 , y3 , z3 ) в базисе {i , j , k }, то
x1 y1 z1
(a , b , c ) x2 y2 z2 .
x3 y3 z3
89.
Теорема.Для компланарности ненулевых
векторов a , b , c необходимо и
достаточно, чтобы (a, b , c ) 0.
90.
Смешанное произведениевекторов обладает свойствами:
1) ([a, b ], c ) (a,[b , c ]);
2) (a, b , c ) (b , c , a ) (c , a, b )
(b , a, c ) (c , b , a ) (a, c , b ).
91.
Тройка векторов a, b , c являетсяправой тогда и только тогда, когда
(a, b , c ) > 0, и левой, когда
(a, b , c ) < 0.
92.
Рассмотрим приложениясмешанного произведения.
93.
Объем V параллелепипеда,построенного на векторах a, b , c :
V (a , b , c ) .
94.
Объем V пирамиды,построенной на векторах a, b , c :
1
V (a , b , c ) .
6
95.
96. § 6. Полярная система координат
97.
98.
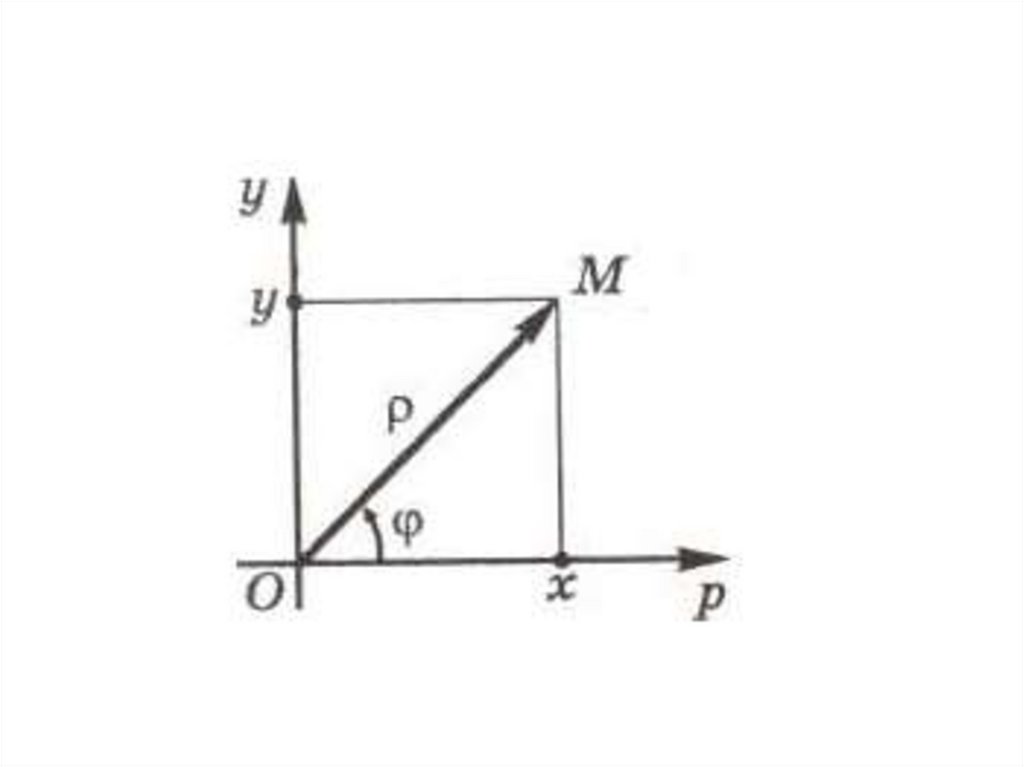
Здесь O – полюс, Op – полярнаяось, ρ – полярный радиус,
φ – полярный угол.
99.
В полярной системе координатположение точки M определяется
парой чисел (ρ, φ) – полярными
координатами точки M, где
ρ OM , φ (Op, OM ).
100.
101.
Формулы перехода к декартовымкоординатам (полюс O совпадает с
началом координат системы Oxy,
полярная ось Op – с осью Ox) имеют
вид:
102.
x ρ cos φ,y ρsin φ,
где 0 ρ < , 0 φ < 2π
(или π < φ π).
103.
104. § 7. Цилиндрическая система координат
105.
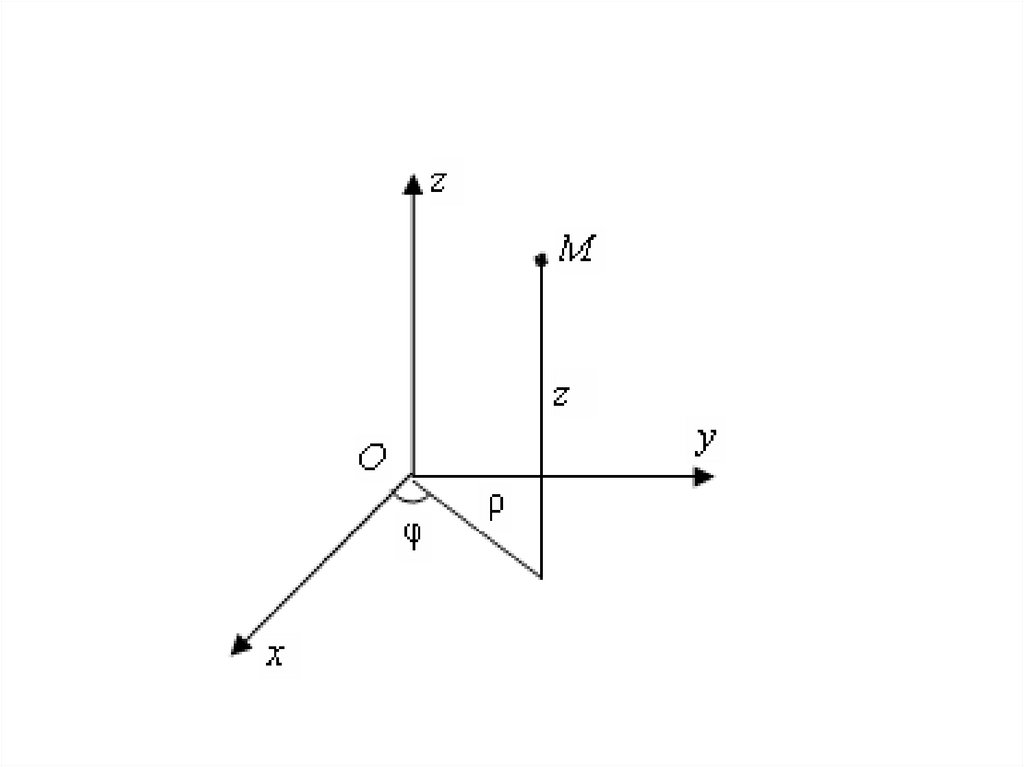
В цилиндрической системекоординат положение точки M
определяется тройкой чисел
(ρ, φ, z) – цилиндрическими
координатами точки M, где (ρ, φ) –
полярные координаты проекции
точки M на плоскость xOy,
z – аппликата точки M.
106.
107.
Формулы перехода к декартовымкоординатам имеют вид:
x ρcosφ,
y ρsin φ,
z z,
где 0 ρ < , 0 φ < 2π,
–∞ < z < ∞.
108.
109. § 8. Сферическая система координат
110.
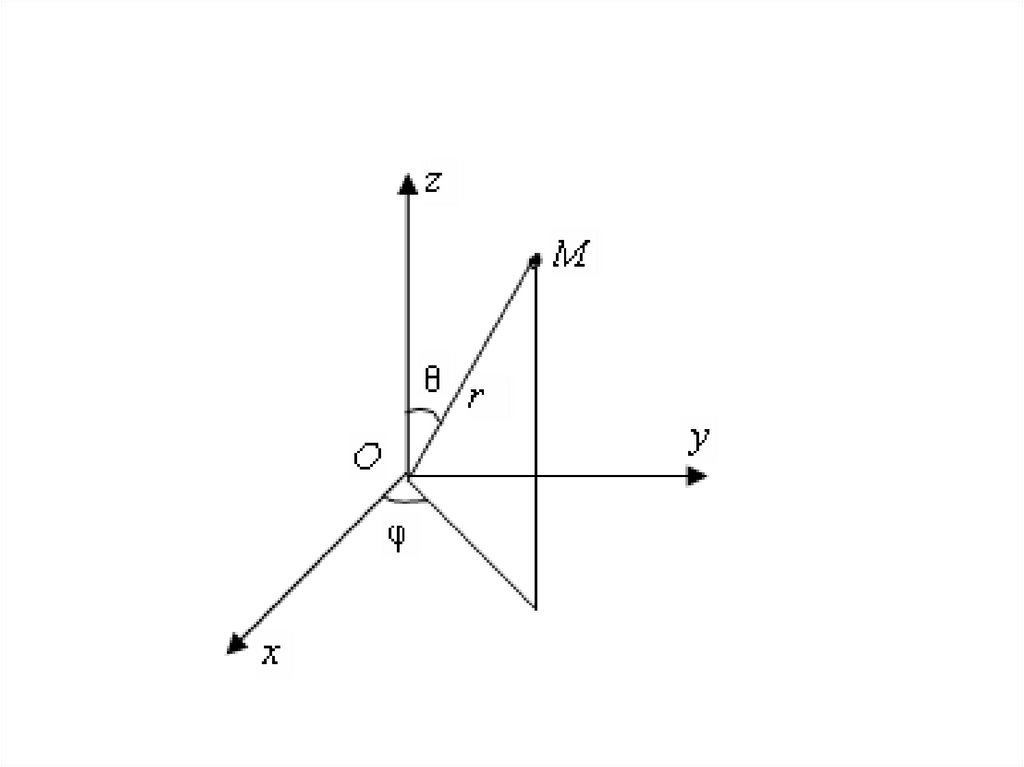
В сферической системекоординат положение точки M
определяется тройкой чисел
(r, θ, φ) – сферическими
координатами
точки
M,
где
r
OM
,
θ (Oz, OM ), φ – полярный угол
проекции точки M на плоскость xOy.
111.
112.
Формулы перехода к декартовымкоординатам имеют вид:
x r cosφsin θ,
y r sin φsin θ,
z r cosθ,
где 0 r < , 0 φ < 2π, 0 θ π.
113.
Высшее назначение математикикак раз и состоит в том, чтобы
находить скрытый порядок в
хаосе, который нас окружает.
Н. Винер















































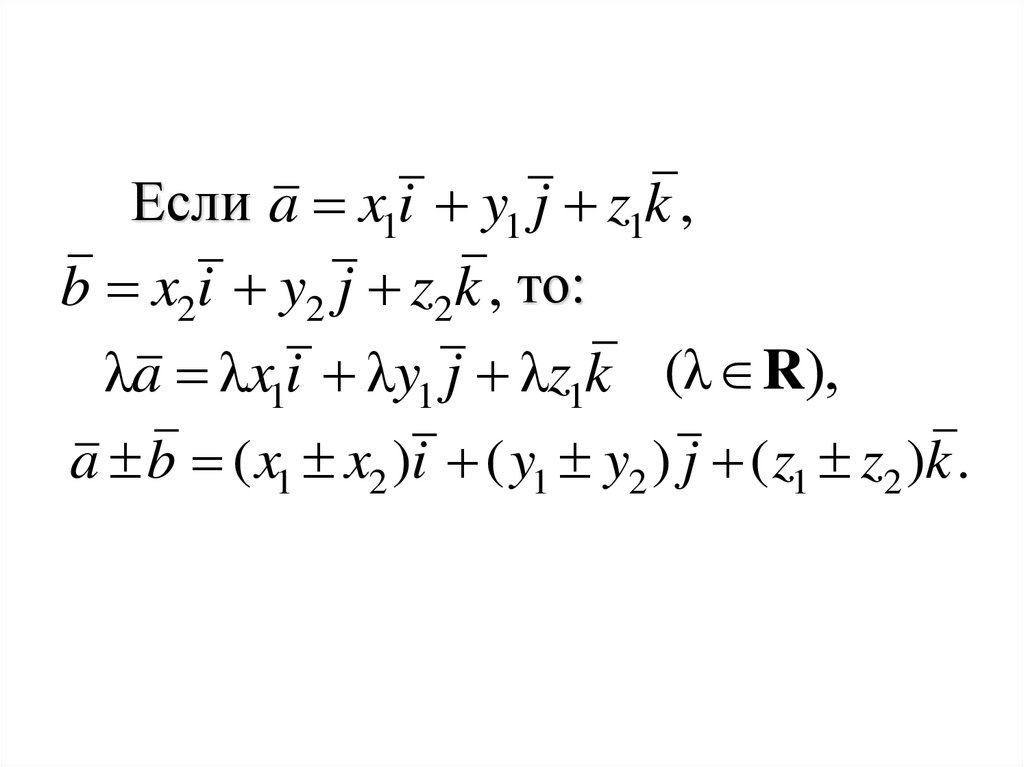






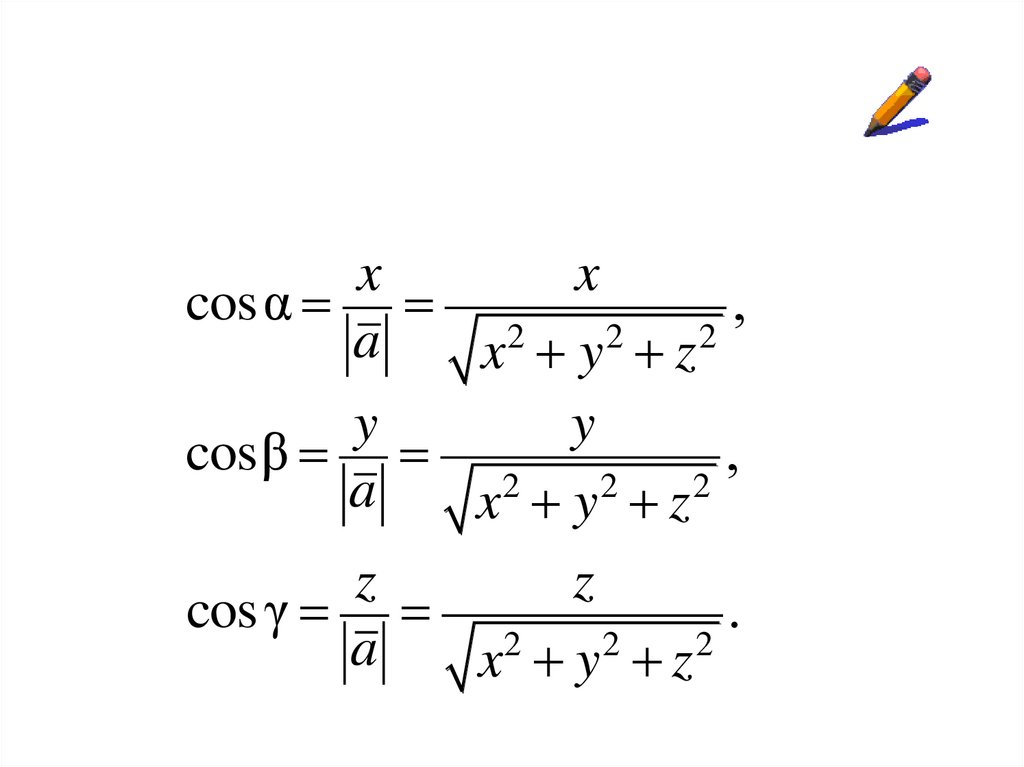




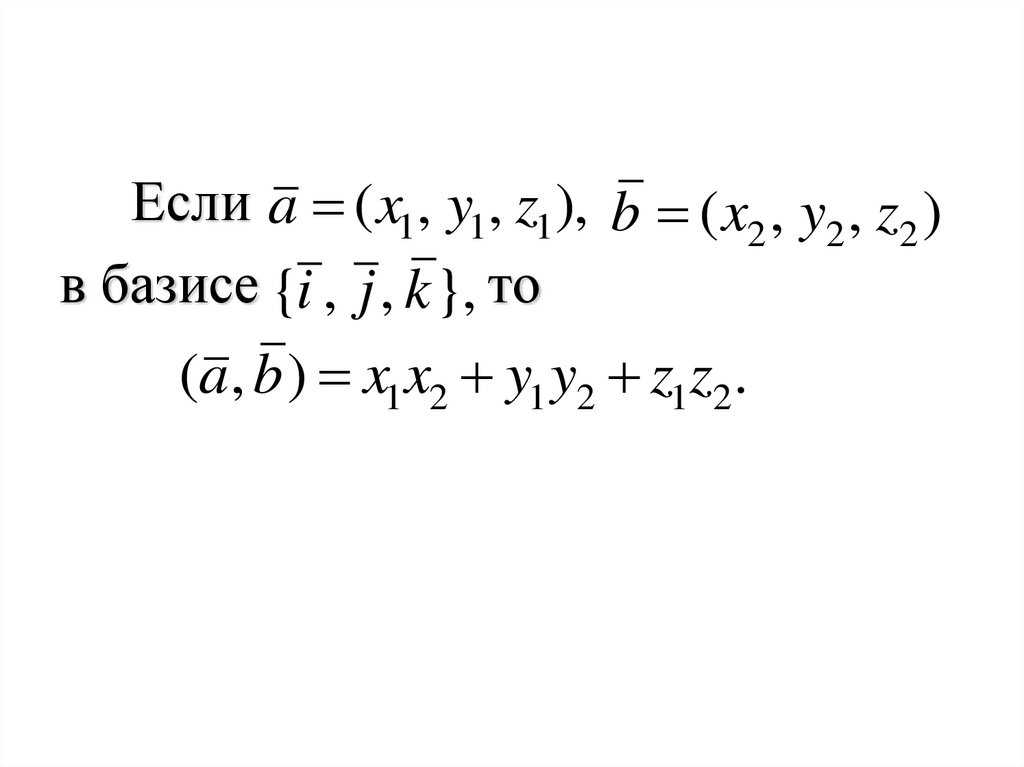




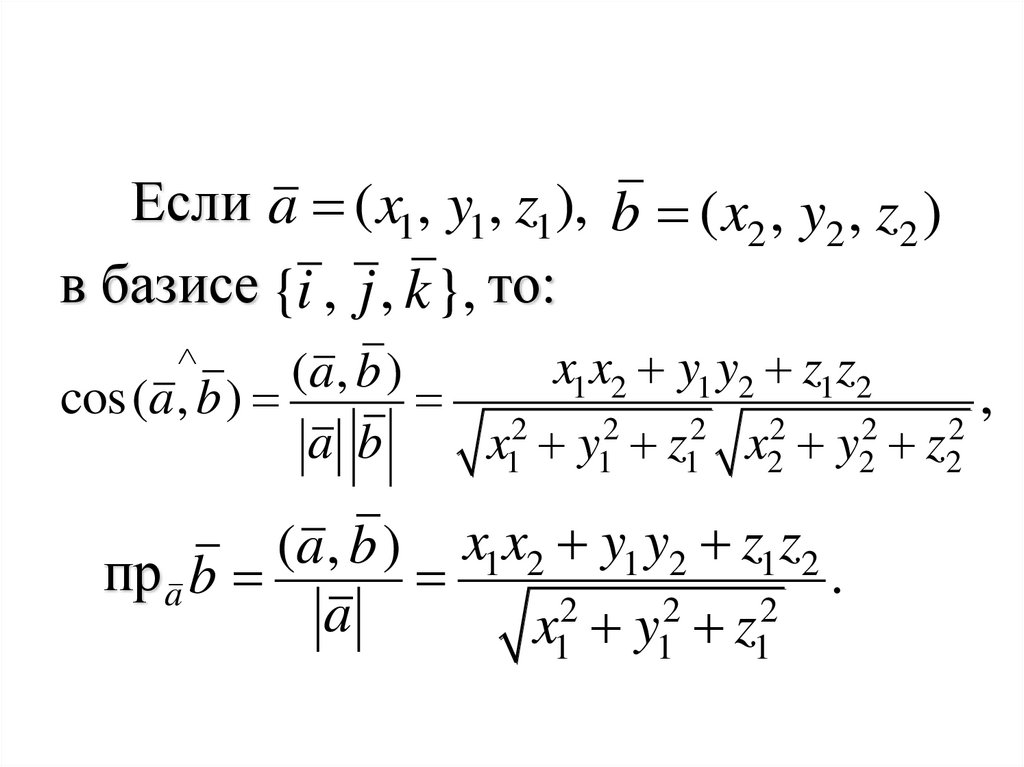







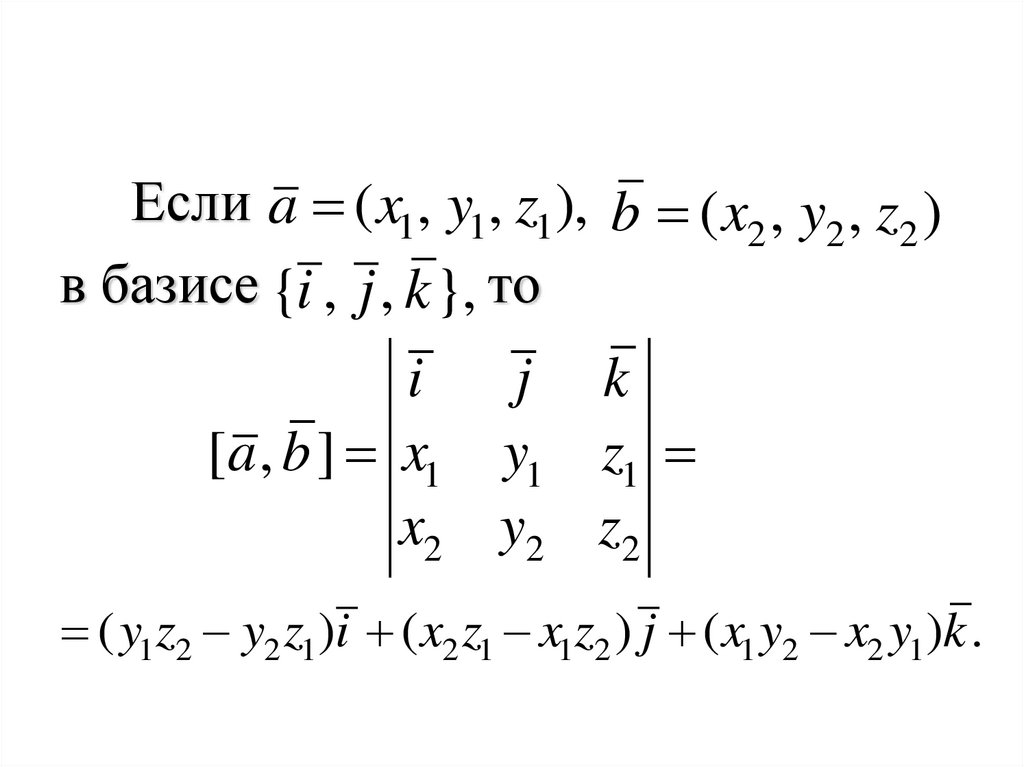



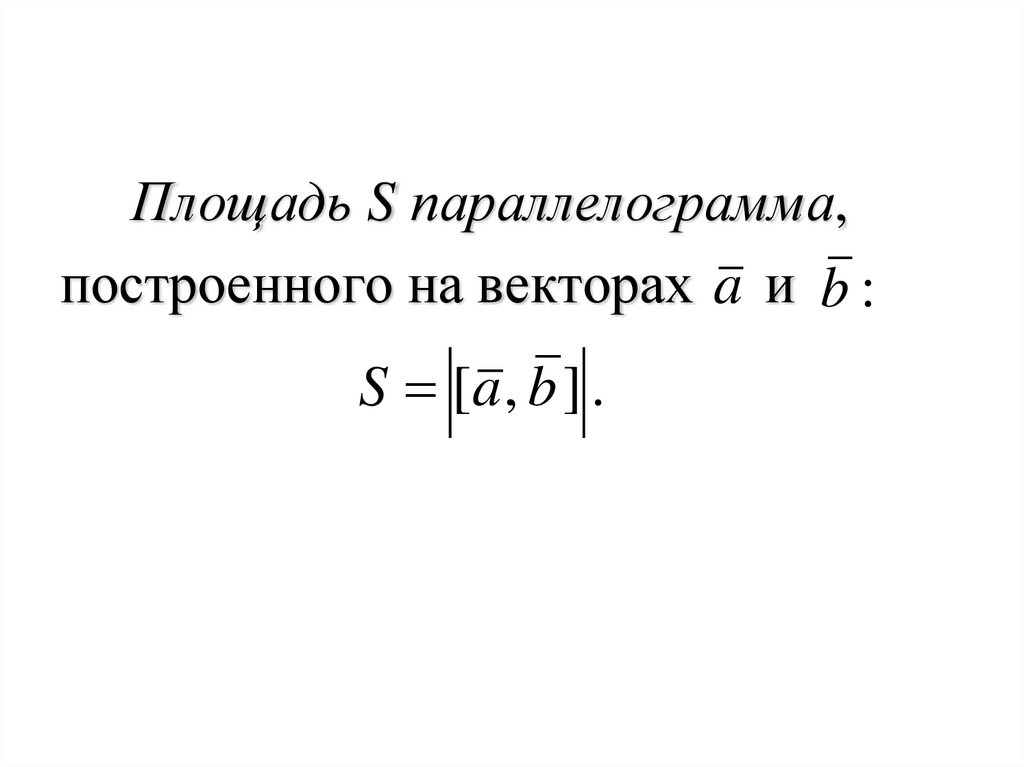
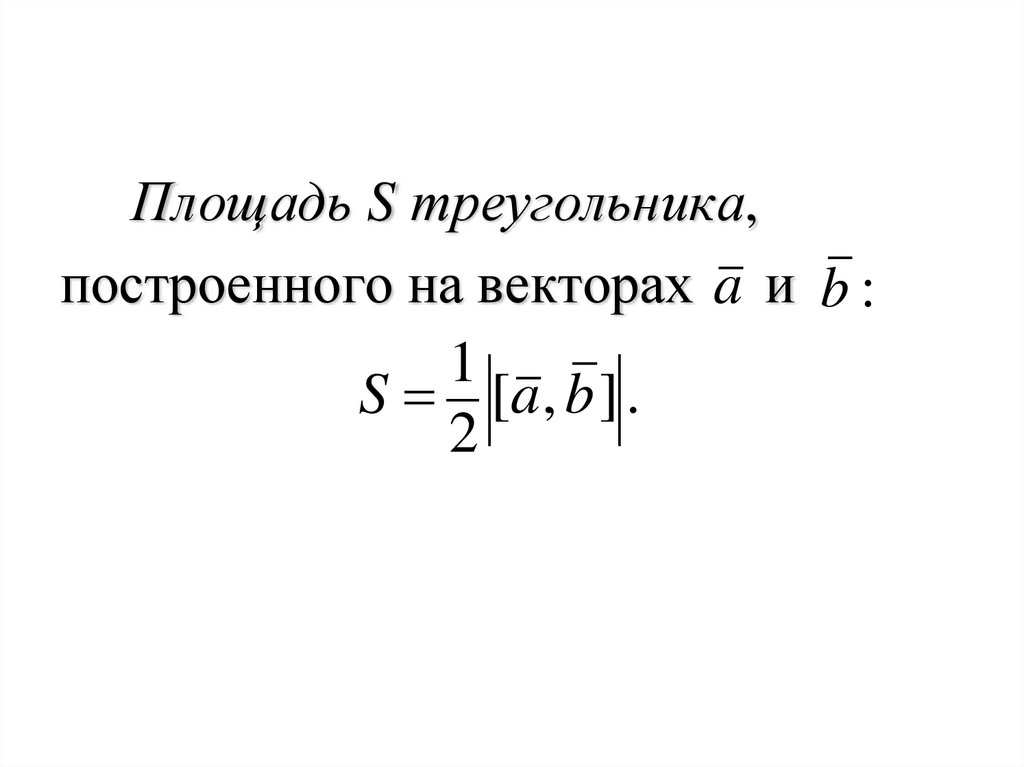




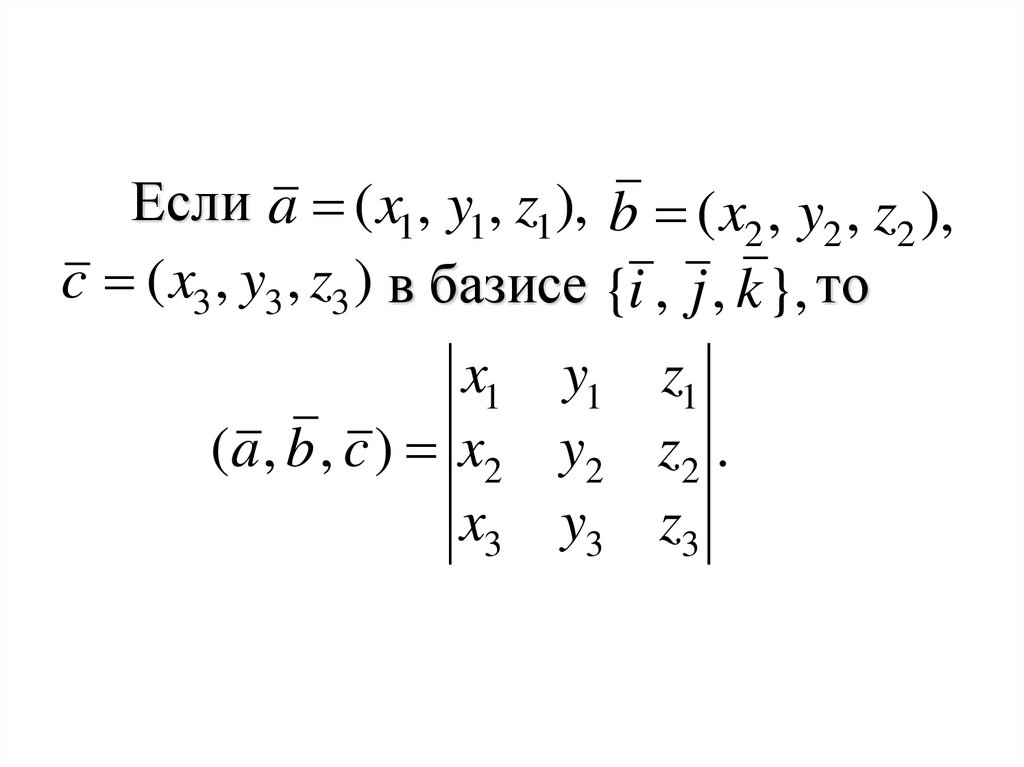





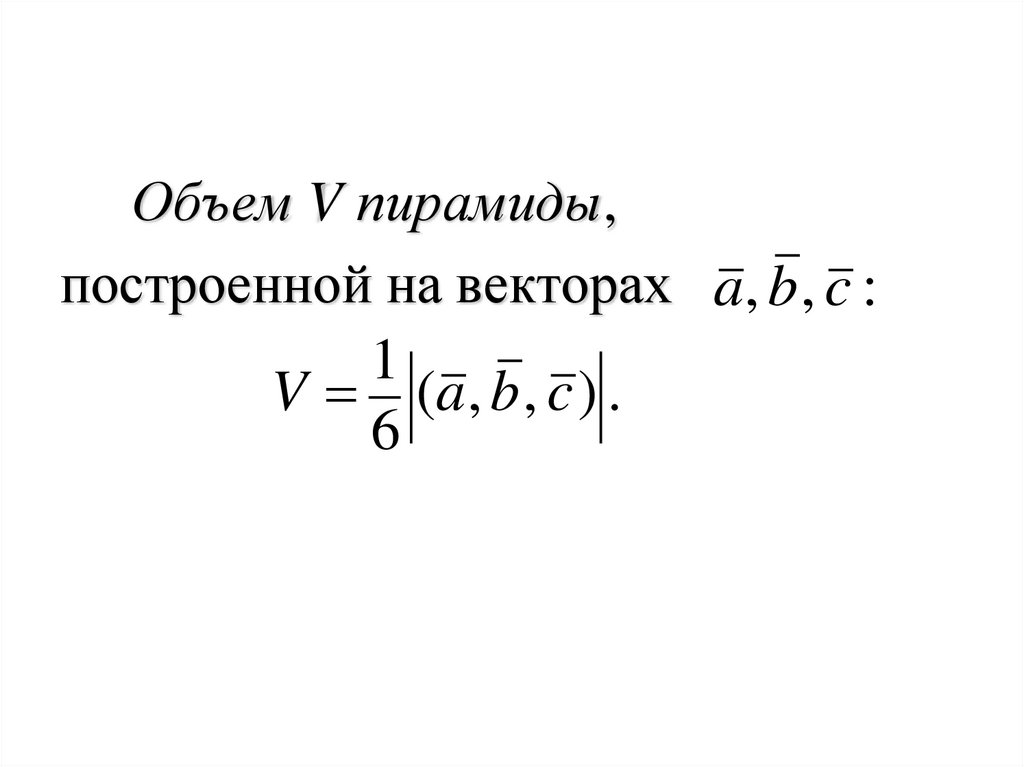






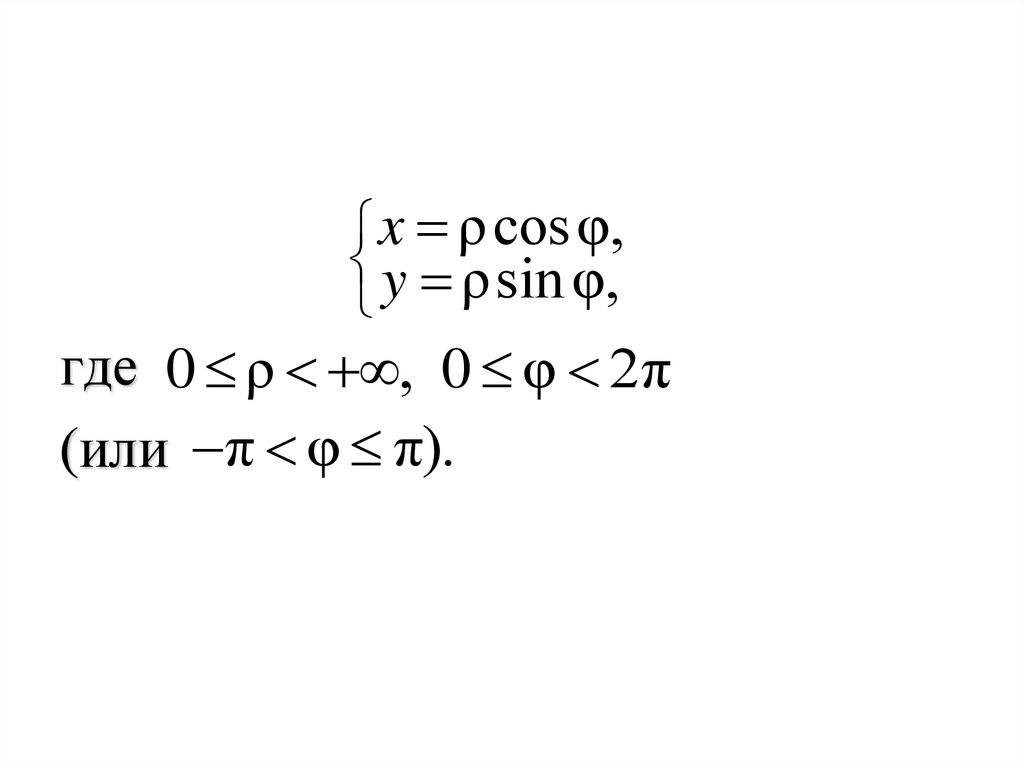









 mathematics
mathematics








