Векторная алгебра (лекция 11)

1. Векторная алгебра

Лекция 11

2. 1. Векторы. Основные понятия

Величины, которые определяются заданием некоторого
называются с к а л я р н ы м и (длина, температура, масса).
числа,
Величины, которые определяются заданием не только числа, но и
некоторого направления, называются в е к т о р н ы м и (сила, скорость,
ускорение).
Векторные величины геометрически изображаются с помощью векторов.
В е к т о р – это направленный отрезок.
Если А – начало вектора, а В – его конец, то вектор обозначается
символом AB
. Вектор можно обозначать одной строчной буквой латинского
алфавита a , b , c ,
Вектор BА называется п р о т и в о п о л о ж н ы м вектору AB .
Д л и н о й или м о д у л е м вектора называется расстояние между его
началом и концом и обозначается AB или a .
Вектор, у которого начало и конец совпадают, называется н у л е в ы м и
обозначается 0 , и его длина равна нулю, т.е. 0 0 .

3.

Вектор, длина которого равна единице, называется е д и н и ч н ы м
вектором и обозначается е .
Единичный вектор, направление которого совпадает с направлением a ,
называется о р т о м вектора a и обозначается a 0 .
Векторы называются к о л л и н е а р н ы м и , если они лежат на одной
прямой или на параллельных прямых.
Два вектора a и b называются р а в н ы м и , если они:
1) имеют одинаковые длины;
2) коллинеарны;
3) одинаково направлены.
В этом случае пишут a b .
Векторы называются к о м п л а н а р н ы м и , если они лежат в одной
плоскости или в параллельных плоскостях.
Если векторы взаимно перпендикулярны
ортогональными.
a b , то они называются

4. 2. Линейные операции над векторами

К линейным операциям над векторами относятся сложение и вычитание
векторов, а также умножение вектора на число.
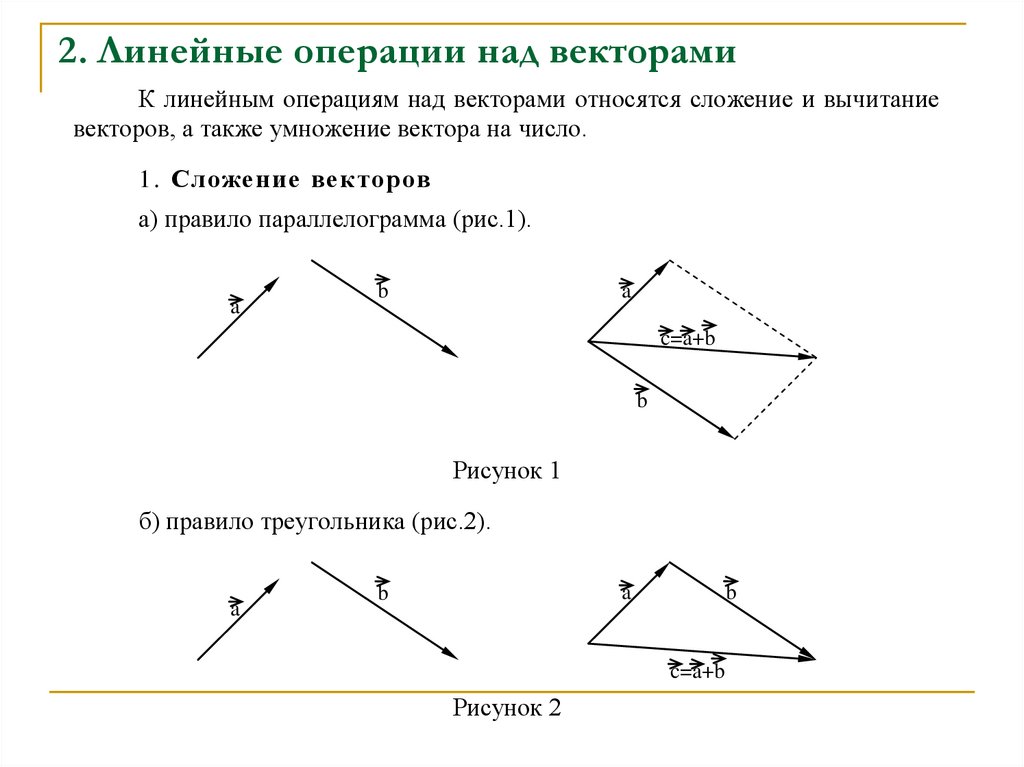
1. Сложение векторов
а) правило параллелограмма (рис.1).
a
b
a
c=a+b
b
Рисунок 1
б) правило треугольника (рис.2).
a
a
b
b
c=a+b
Рисунок 2

5.

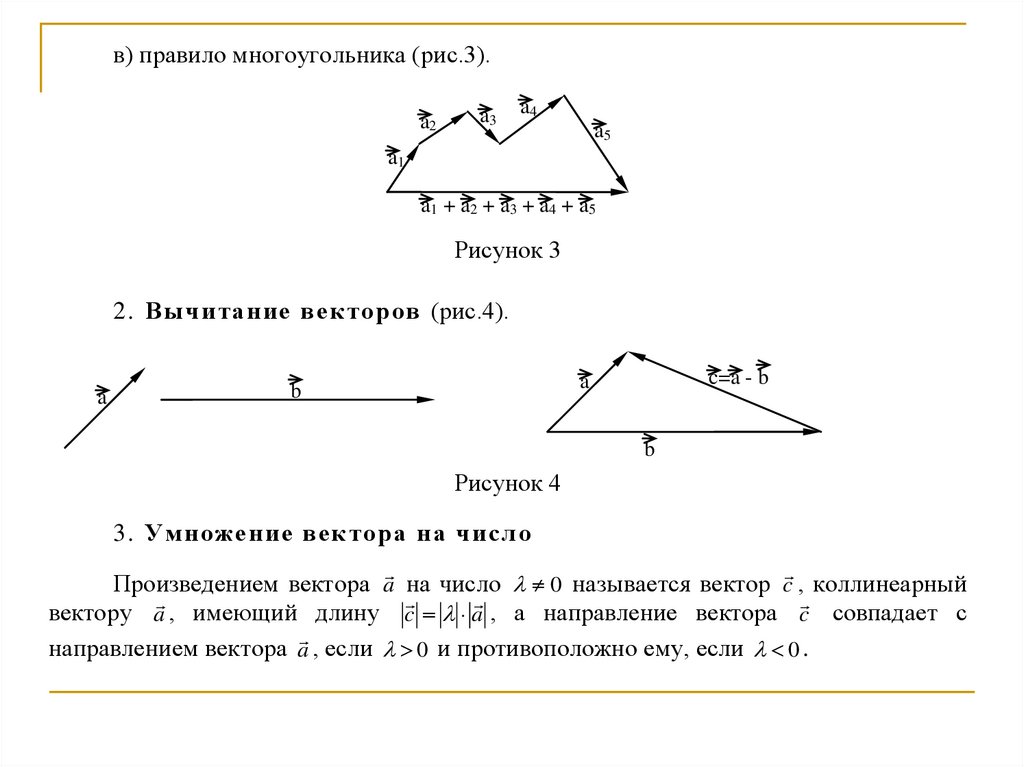
в) правило многоугольника (рис.3).
a2
a3
a4
a5
a1
a1 + a2 + a3 + a4 + a5
+
Рисунок 3
2. Вычита ние ве кторов (рис.4).
a
c=a - b
a
b
b
Рисунок 4
3. Умножение вектора на числ о
Произведением вектора a на число 0 называется вектор c , коллинеарный
вектору a , имеющий длину c a , а направление вектора c совпадает с
направлением вектора a , если 0 и противоположно ему, если 0 .

6.

Приведем некоторые свойства линейных операций:
1) a b b a ,
2) a b c a b c ,
3) 1 2a 1 2 a ,
4) 1 2 a 1 a 2 a ,
5) a b a b .

7. 3. Проекция вектора на ось

Пусть в пространстве заданы ось l и некоторый вектор AB . Обозначим
через А1 и В1 проекции на ось l соответственно начала А и конца В этого
вектора (рис.5).
Рисунок 5
Проекцией
вектора
AB
на ось l
называется величина
направленного отрезка А1В1 и обозначается прl АВ А1В1 .
Некоторые ос новные свойс тва проекций
1) Проекция вектора a на ось l равна
прl a a cos , где a , l .
А1В1

8.

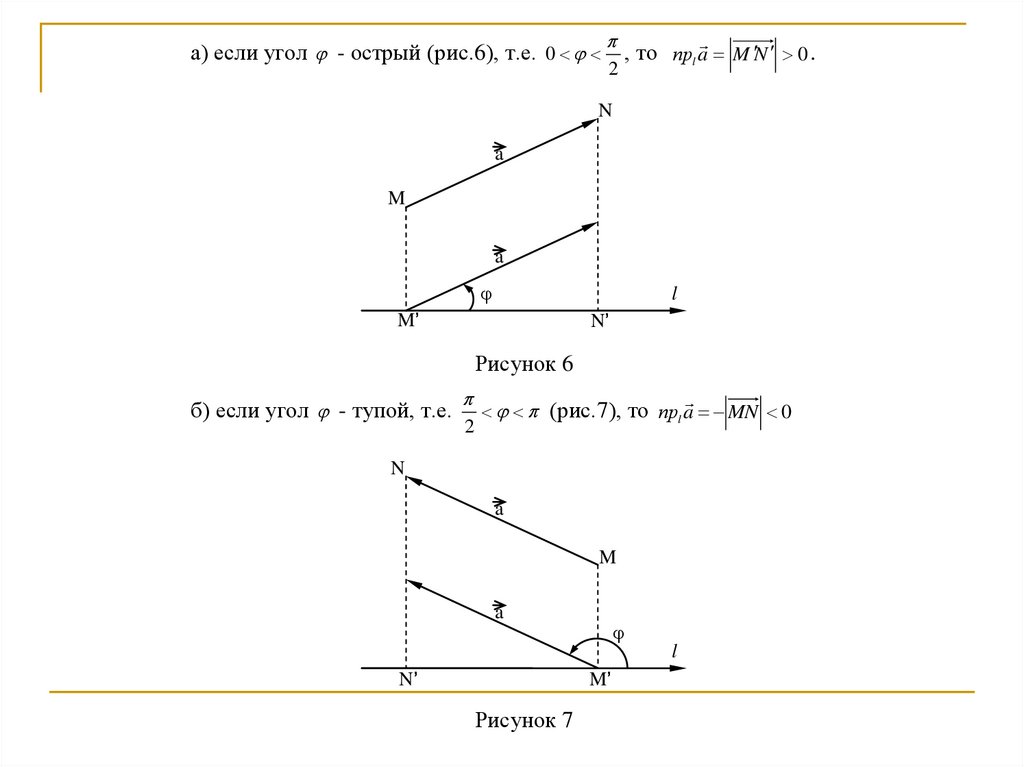
а) если угол - острый (рис.6), т.е. 0
2
, то прl a M N 0 .
N
a
M
a
φ
l
M’
N’
Рисунок 6
б) если угол - тупой, т.е.
2
(рис.7), то прl a MN 0
N
a
M
a
φ
l
M’
N’
Рисунок 7

9.

в) если угол - прямой, т.е.
2
(рис.8), то прl a 0
a
2
Рисунок 8
2) Проекция суммы двух векторов на ось равна сумме проекций
слагаемых на ту же ось, т.е.
прl a b прl a прl b .
3) Если вектор a умножить на число , то его проекция на ось также
умножится на это число, т.е.
прl a прl a .

10. 4. Линейная зависимость векторов

Векторы а1, а2 , ..., аn называются л и н е й н о з а в и с и м ы м и ,
если существуют числа 1 , 2 , ..., n не все равные нулю, для которых
имеет место равенство 1 а1 2 а2 ... n аn 0 .
Векторы а1, а2 , ..., аn называются л и н е й н о н е з а в и с и м ы м и ,
если равенство
1 а1 2 а2 ... n аn 0 имеет место только при
1 2 ... n 0 .
Теорема 1. Всякие три вектора a , b и c на плоскости линейно
зависимы.
Теорема 2. Для того, чтобы два вектора a и b были линейно
независимы, необходимо и достаточно, чтобы они были неколлинеарны.
Теорема 3. Всякие четыре вектора a , b , c и d в пространстве
линейно зависимы.
Теорема 4. Для того, чтобы три вектора a , b и c были линейно
независимы, необходимо и достаточно, чтобы они были некомпланарны.

11. 5. Базис на плоскости и в пространстве

Б а з и с о м н а п л о с к о с т и называются два линейно независимых
вектора этой плоскости, взятых в определенном порядке.
Теорема. Если векторы а1 и а2 образуют базис на плоскости, то всякий
вектор а этой плоскости может быть единственным образом разложен в виде
линейной комбинации векторов а1 и а2 :
а 1 а1 2 а2 .
Числа 1 и 2 называют аффинными координатами вектора a на
плоскости и пишут а 1 ; 2 .
Б а з и с о м в п р о с т р а н с т в е называются три любых линейно
независимых вектора.
Теорема. Если в пространстве выбран некоторый базис а1 , а2 , а3 , то
любой вектор а этого пространства может быть единственным образом
разложен по этому базису в виде
а 1 а1 2 а2 3 а3 ,
где 1 , 2 , 3 - аффинные координаты вектора а в пространстве.
Пишут а 1 ; 2 ; 3 .

12. 6. Разложение вектора по ортам координатных осей. Модуль вектора

Рассмотрим в пространстве прямоугольную систему координат Oxyz . Пусть i , j , k
единичные векторы (орты) осей координат, т.е. i j k 1 , и одинаково направлены
соответственно с осями OX , OY и OZ .
Так как орты i , j , k не компланарны, то они образуют базис, который называется
декартовым ортогональным базисом .
z
М
k
О
i
j
х
Рисунок 9
у

13.

Возьмем любой вектор a пространства и совместим его начало с
a
ОМ
началом координат:
(рис.9).
Можно показать, что вектор a можно представить в виде а х i у j z k ,
где x прОХ а , y прОУ а , z прОZ а и вектор a записывают в виде а x ; y; z .
Числа x, y, z называют п р я м о у г о л ь н ы м и
координатами.
декартовыми
Зная координаты вектора а x, y, z можно найти его длину по формуле
а x2 y 2 z 2 .
Пусть вектор а x, y, z образует с осями координат OX , OY и OZ
x
a
y
a
z
a
соответственно углы , , , тогда cos , cos , cos
называются н а п р а в л я ю щ и м и к о с и н у с а м и вектора a .
Можно показать, что сумма квадратов направляющих косинусов
ненулевого вектора равна единице, т.е. cos 2 cos 2 cos 2 1 .
0 а
Заметим, что орт вектора а x, y, z находится по формуле а , т.е.
а
а 0 cos , сos , сos .

14. 7. Действия над векторами, заданными координатами

Пусть даны векторы a x1 ; y1; z1 и b x2 ; y 2 ; z 2 , тогда:
1) a b x1 x2 ; y1 y2 ; z1 z 2
2) a x1; y1 ; z1 , ( const )
x1 x2
3) a b y1 y2 – условие равенства векторов
z z
2
1
4) a || b
x 1 y1 z 1
- условие коллинеарности векторов.
x 2 y2 z2
Если известны координаты точек А x1, y1, z1 и B x2 , y2 , z2 , то координаты
вектора AB равны разностям соответствующих координат его конца и начала,
т.е.
AB x2 x1; y2 y1; z2 z1 .

15. 8. Скалярное произведение векторов

С к а л я р н ы м п р о и з в е д е н и е м двух векторов a и b называется
число, равное произведению длин этих векторов на косинус угла между ними
a b a b cos , где (a b ) .
Свойства скалярного произведения
1) a b b a ;
2) a (b c ) a b a c ;
3) ( a ) b (a b ) , const ;
2
4) a a a 2 a ;

16.

5) a 2 a ;
6) a b 0 , если a b или a 0 , или b 0 ;
a b
7) cos , (a b ) ;
a b
a
b
8) npb a ;
b
F , действующей на материальную точку при перемещении
9) работа силы
ее вдоль вектора S , вычисляется по формуле A F S ;
10) i 2 j 2 k 2 1,
i j i k j k 0 , где i , j , k - орты осей координат;
11) если a x1 ; y1 ; z1 и b x 2 ; y 2 ; z 2 , то a b x1 x 2 y1 y 2 z1 z 2 .

17. 9. Векторное произведение векторов

Упорядоченная тройка некомпланарных векторов a , b , c с общим началом
называется п р а в о й , если кратчайший поворот от вектора a к вектору b
происходит против движения часовой стрелки, если наблюдать с конца вектора c . В
противном случае тройка векторов называется л е в о й (рис.10).
c
c
b
a
a
b
a , b , c - правая тройка
a , b , c - левая тройка
Рисунок 10
В е к т о р н ы м п р о и з в е д е н и е м векторов a и b называется вектор c ,
обозначаемый c a b , который удовлетворяет следующим условиям:
1) c a b a b sin , где (a b ) ;
2) c a , c b ;
3) a , b , c - правая тройка.

18.

Свойства векторного произведения
1) a b b a ;
2) a ( b + с ) = a b + a с ;
3) ( a ) b = ( a b )= a ( b );
4) a a 0 ;
5) a b 0 a b ;
6) S a b , где S – площадь параллелограмма, построенного на векторах a и b
(рис.11);
c
b
φ
O
a
Рисунок 11

19.

7) S
1
a b , где S - площадь треугольника, построенного на векторах a и b ;
2
8) M OA F , где M - момент силы F , приложенной к точке А, относительно
точки О;
i j j i k ,
9) i i j j k k 0 ,
j k k j i ,
10) если a = x1 ; y1 ; z1 и b = x2 ; y2 ; z 2 , то
i
а b x1
x2
j
y1
y2
k
z1
z2
или
y1
a b =
y2
zz
;
z2
x1
x2
zz
;
z2
x1
x2
yz
.
y2
k i i k j

20. 10. Смешанное произведение векторов

С м е ш а н н ы м п р о и з в е д е н и е м векторов a , b , c называется
число, равное скалярному произведению вектора a b на вектор c и
обозначается (a b ) c или a b c .
О с н о в н ы е с в о й с т в а с м е ш а н н о г о п р о и з в е д е н и я
1) (a b ) c a (b c ) ;
2) a b c = b c a = c a b ;
3) a b c >0, если a , b , c - правая тройка,
a b c <0, если a , b , c - левая тройка;
4) a b c 0 a , b , c - компланарны;
5) Объем параллелепипеда, построенного на векторах a , b , с , вычисляется по
формуле
V a b с ;
6) Объем треугольной пирамиды, построенной на векторах a , b и c
1
V a b c ;
6
x1 y1 z1
7) Если a x1 ; y1 ; z1 , b x2 ; y2 ; z 2 , c x3 ; y3 ; z3 , то a b c x 2 y 2 z 2 .
x3 y 3 z 3

21.

Пример. Даны точки A(10,6,3) , B ( 2,4,5) , C (3, 4, 6) и D(0, 1,2) .
а) Найти длину вектора 5 AB 2 CD .
Координаты векторов AB 12; 2; 2 и CD 3; 3; 8 ,
найдем координаты вектора 5 AB 2 CD :
5 12; 2; 2 2 3; 3; 8 60 6; 10 6;10 16 54; 16; 6 .
Длину вектора найдем по формуле a x 2 y 2 z 2 , получим
5 AB 2 CD
54 2 16 2 6 2 2916 256 36 3208 2 802 .
б) Найти скалярное произведение векторов AB и AC .
Скалярным произведением векторов AB 12; 2; 2 и AС 7; 10; 9 будет:
АВ АС 12 7 2 10 2 9 84 20 18 86 .

22.

в) Найти косинус угла между векторами AB и AC .
Для нахождения косинуса угла между векторами AB и AC воспользуемся
формулой:
a b
cos .
a b
Для этого найдем длины векторов AB и AC :
12 2 2 2 2 2 144 4 4 152 2 38 ,
7 2 10 2 9 2 49 100 81 230 .
AB
AС
Тогда
cos
AB AC
AB AC
86
43
43
.
2 38 230
8740 2 2185
г) Найти проекцию вектора AB на направление вектора AC .
c d
Проекцию вектора AB на направление вектора AC найдем по формуле: прd c .
d
Получим
пр АВ
АС
86
.
230

23.

д) Найти площадь треугольника ABC .
Из определения векторного произведения площадь треугольника ABC равна:
S АВС
1
AB AC .
2
Найдем векторное произведение векторов AB и AC :
i
j
k
2 2
12 2
12 2
AB AC 12 2 2
i
j
k ,
10 9
7 9
7 10
7 10 9
AB AC 38i 122 j 106k , т.е. AB AC 38; 122; 106
AB AC 38 2 122 106 2 1444 14884 11236 27564 2 6891
2
Таким образом, S ABC 6891 кв.ед.

24.

е) Найти объем пирамиды DABC .
Из свойств смешанного произведения векторов имеем:
Vпир
1
AB AC AD
6
.
Зная координаты векторов:
AB 12; 2; 2 , AC 7; 10; 9 , AD 10; 7; 1 ,
вычислим
12 2 2
6 1 1
AB AC AD 7 10 9 2 7 10 9
10 7 1
10 7 1
2 60 90 49 100 7 378 2 184 368
1
184
Vпир 368
6
3
Vпир 61
1
куб .ед.
3