Similar presentations:
Векторная алгебра
1. Векторная алгебра
теоретический курс2.
Содержание1. Вектор
а) Операции над векторами
б) Свойства сложения векторов
в) Свойства умножения векторов
2. Линейная зависимость и независимость векторов
а) Свойства линейно зависимых и линейно независимых систем векторов
б) Геометрический смысл линейной зависимости и независимости векторов
3. Базис на плоскости и в пространстве
4. Векторное пространство
5. Аффинная система координат
а) Простейшие задачи в АСК
6. Проекция вектора на ось
7. Прямоугольная декартова система координат (ПДСК)
а) Длина вектора. Расстояние между двумя точками в ПДСК
3.
8. Скалярное произведение векторова) Геометрический смысл скалярного произведения
б) Алгебраические свойства скалярного произведения
в) Скалярное произведение в координатах
9. Векторное произведение векторов
а) Геометрические свойства векторного произведения
б) Алгебраические свойства векторного произведения
в) Векторное произведение в координатах
г) Применение векторного произведения
10. Смешанное произведение векторов
а) Геометрический смысл смешанного произведения
б) Алгебраические свойства смешанного произведения
в) Смешанное произведение в координатах
г) Применение смешанного произведения
11. Двойное векторное произведение
4. Вектор
Нам уже известно, что два луча называются параллельными, еслиони лежат на одной или параллельных прямых.
Определение №1
Два луча плоскости называются сонаправленными, если
выполняются условия:
1) если лучи лежат на параллельных прямых;
2) если через начало лучей провести прямую, то оба луча будут
лежать по одну сторону от прямой.
Определение №2
Два луча плоскости называются противоположно направленными,
если выполняются условия:
1) лучи лежат на параллельных прямых;
2) если через начало лучей провести прямую, то оба луча будут
лежать по разные стороны от прямой.
Если параллельные лучи лежат на одной прямой, то их
сонаправленность означает, что один луч лежит внутри другого.
назад к содержанию
5.
Определение №3Рассмотрим множество всех сонаправленных лучей – это
направление на плоскости.
Определение №4
Два луча пространства называются сонаправленными, если
выполняются условия:
1) эти лучи лежат на параллельных прямых:
2) если через начало лучей провести плоскость, не содержащую
этих лучей, то оба луча будут расположены по одну сторону от
этой плоскости.
Определение №5
Множество всех сонаправленных лучей пространства –
направление пространства.
Определение №6
Вектор - направленный отрезок, имеющий начало и конец.
Определение №6.1
Вектор - упорядоченная пара точек, т.е. пара точек, одна из
которых является первой, другая второй ( AB, AB).
Вектор характеризуется длиной и направлением.
6.
Определение №7Луч называется соотнесенным с данным вектором, если начало
вектора является началом луча, а конец вектора принадлежит
лучу.
рис. 1
Определение №8
Направление вектора – направление соотнесённого с ним луча.
Определение №9
Длина вектора – расстояние между началом и концом.
Чтобы задать вектор, нужно задать:
• начало,
• направление (соотнесённый луч),
• длину.
Определение №10
Два вектора называются коллинеарными, если их соотнесенные
лучи параллельны (лежат на одной или параллельных прямых).
7.
Определение №11Два вектора называются сонаправленными, если их соотнесенные
лучи сонаправлены.
Определение №12
Равные векторы - сонаправленные векторы, имеющие
одинаковые длины.
8.
Критерий равенства двух векторов:AB CD ABDC параллелограмм
Док-во:
Необходимость.
AB CD , A, B, C, D – не лежат на одной прямой. Получаем
трапецию ABDC, так как стороны AB CD параллельны.
Получаем, что ABDC – параллелограмм, так как AB CD .
рис. 2
Достаточность.
ABDC – параллелограмм. То есть AB CD , по свойству
параллелограмма и коллинеарны AB || CD . Допустим AB CD .
Но фигура ABDC не является параллелограммом
рис. 3
AB CD AB CD .
Определение №13
Множество всех равных между собой векторов называется
свободным вектором.
9. Линейные операции над векторами
1) Сложение векторовОпределение №14
Говорят, что вектор c a b, если будучи приложенным к началу вектора a
, его конец будет совпадать с концом b , причём конец a
совпадает с началом b .
рис. 4
2) Операция умножения вектора на число
Определение №15
Вектор b называется произведением числа на вектор a ( b a ),
если:
1.
b || a
2.
| b | | | | a |
(коллинеарность)
3. 0 b a , 0 b a
назад к содержанию
10. Свойства сложения векторов:
1. Коммутативность сложения векторов a b b a .2. Ассоциативность сложения векторов ( a b) c a (b c ) .
3. o : a : a o o a a
4. a : a ' : a a ' o, a ' - противоположный к a .
назад к содержанию
11. 1. Коммутативность сложения векторов
a b b aДок-во:
От точки А откладываем вектор a , получаем точку В. От точки В
откладываем вектор b, получаем точку С. Проводим вектор a b ,
начало которого в точке А, а конец в точке С.
От точки А откладываем вектор b , получаем точку D. От точки D,
откладываем вектор a , получаем точку C’. Проводим вектор b a ,
начало которого в точке А, а конец в точке C’.
Пусть C и C’ не совпадают. Рассмотрим вектор BC,'
так как AB DC ' a Значит AD BC ' b . По критерию равенства
векторов ABC' D
b BC(по построению), b BC ' (доказали ранее) BC BC ' C C' .
Получили противоречие, следовательно, наше предположение неверно,
значит C и C’ совпадают. Отсюда следует a b b a AС.
рис. 5
12.
Правило параллелограммаОпределение №16
Приложим вектора a и b к одной точке и достроим до параллелограмма.
Тогда суммой двух векторов будет вектор, совпадающий с диагональю
параллелограмма, начало которой совпадает с общим началом a и b .
рис.6
13.
2. Ассоциативность сложения векторов(a b) c a (b c)
Док-во:
a b AC
(a b) c AC CD AD
b c BD
a (b c) AB BD AD
(a b) c a (b c)
рис.7
Следствие: правило сложения n-векторов
Первый вектор прикладываем к точке, начало следующего вектора должно
совпадать с концом предыдущего. Тогда сумма векторов есть вектор,
начало которого совпадает с началом первого, а конец с концом
последнего.
рис. 8
14.
3. o : a : a o o a aДок-во:
Рассмотрим вектор a AB; AB O AB В силу правила треугольника
O BB , O AB AB O AA.
Определение №17
Нулевой вектор есть пара совпадающих точек.
15.
4. a : a' : a a' o, a' - противоположный к a .Док-во:
Рассмотрим вектор a AB , тогда AB a' 0 AA a' BA
Проверка: AB BA AA, a ' a , т. е. BA AB
Следствие: операция вычитания
Рассмотрим сумму векторов a b c . b ?
a b a c a b 0 c a b c a
16. Свойства умножения вектора на число:
1.Дистрибутивность относительно сложения векторов : a b a b
3.
a a a
Ассоциативность умножения вектора на число : a a
4.
1 a a
2.
Дистрибутивность относительно сложения чисел :
назад к содержанию
17. Дистрибутивность относительно сложения векторов :
1.Дистрибутивность относительно
сложения векторов :
a b a b
Док-во:
Рассмотрим 4 случая:
а) b не коллинеарен a , 0
a AB, b AC , a b AD, a AB', b AC ', a b AD'
AB`C`D` - параллелограмм
ABD AB' D' (по двум сторонам и углу между ними), причём коэффициент
подобия – λ.
ADC AD'C' (по трём углам), причём из ABD AB' D' , следует, что
коэффициент подобия ADC и AD'C ' – λ.
Из ADC AD'C' следует по определению AC' AC AC' AC.
AB`D`C`- параллелограмм, следовательно, по свойству параллелограмма
b a
AB' AC ' AD' a b a b
рис.9
18.
б) b не коллинеарен a , 0Рассуждения аналогичны.
в) b коллинеарен a , 0
AB BC AC a b
A' B ' B ' C ' A' C '
a b a b
A' SB ' ASB (по двум углам) т.к. A' C ' AC a b A' C ' AC , A' B' AB
коэффициент подобия равен λ.(по двум углам)
A' SC' ASC(по двум углам), т.к. A`S ` AS, то коэффициент подобия
равен λ.
B`SC` BSC (по двум углам) B`C` BC b .
рис.10
в) b коллинеарен a , 0
Рассуждения аналогичны.
19.
2.Дистрибутивность относительно
сложения чисел : a a a
Док-во: Рассмотрим 6 случаев
1) , 0
2) 0, 0, 0; ( | |)
3) 0, 0, 0; ( | |)
4) 0, 0, 0;
5) 0, 0, 0;
6) , 0
Будем доказывать в каждом случае, что вектора a и a a
сонаправлены и их модули равны.
20.
1), 0
a a, a a, a a
} a a a
a a a, a a a a
a a a a a a a
a a a
По определению равенства векторов a a a
2)
0, 0, 0,
a a, a a, a a
} a a a
a a a a
a a a a a a a
a a a
По определению равенства векторов a a a .
В остальных случаях рассуждения аналогичны.
21.
3.Ассоциативность умножения вектора
на число : a a
Док-во: Рассмотрим 4 случая:
1) , 0
2) 0, 0
3) 0, 0
4) 0, 0
a
Будем доказывать в каждом случае, что вектора a и
сонаправлены и их модули равны.
1) , 0
a a a a a a
a a, a a a
a a, a a
По определению равенства векторов a a
22.
2)0, 0
| ( a ) | | | | a | | | | | | a | | || a | | ( )a | ( ) | a |
( a) a a ( a) a
0 ( )a a ( a) ( a)
По определению равенства векторов a a
В остальных случаях рассуждения аналогичны.
23.
4.1a a
Док-во:
1a 1 a a
1 0 1a a
a коллинеарны и их модули равны, то по
определению равенства векторов 1a a .
Так как вектора 1a и
24.
Теорема 1Для того чтобы a || b R : b a a 0 .
Док-во:
Необходимость.
b
Пусть a || b и a 0 . Пусть
Если
a b 0
Если
a b 0
Если
a
b 0 0
По определению умножения вектора на число
b a
Достаточность.
Если b a по определению умножения вектора на число эти векторы
коллинеарны.
25. Линейная зависимость и независимость векторов
Определение №18Пусть имеем систему из n векторов a1 , a2 ,..., an и имеем набор чисел
1 , 2 ,..., n . Вектор 1 a1 2 a2 ... n an – линейная комбинация
данной системы векторов с данным набором коэффициентов.
Определение №19
Система векторов a1 , a2 ,..., an называется линейно зависимой, если
существует такой набор коэффициентов 1 , 2 ,..., n , из которых хотя бы
один не равен нулю, такой что линейная комбинация данной системы
векторов с этим набором коэффициентов равна нулевому вектору
1 a1 2 a2 ... n an . 0
Определение №20
Система векторов
a1 , a2 ,..., an называется линейно зависимой, если хотя
бы один из векторов этой системы можно представить в виде линейной
комбинации других векторов этой системы.
назад к содержанию
26.
Утверждение №1Определения №19 и№20 эквивалентны.
Док-во:
1)Допустим a1 , a2 ,..., an линейно зависимая система по определению №19.
Тогда существуют 1 , 2 ,..., n из R1 и хотя бы одно из них не равно 0.
Пусть
1 .0
1 a1 2 a2 ... n an 0
Разделим левую и правую части на 1 .
Мы представили вектор a1 в виде линейной комбинации остальных
векторов. По определению №20 система векторов линейно зависима.
2)Допустим a1 , a2 ,..., an линейно зависимая система по определению №20.
a1 2 a2 3 a3 ... n an
a1 2 a2 3 a3 ... n an 0
1 0 . По определению №19 a1 , a2 ,..., an линейно зависимая система
векторов.
Определения №19 и№20 эквивалентны.
27.
Определение №21Система векторов a1 , a2 ,..., an называется линейно независимой, если
нулевая линейная комбинация этой системы возможна лишь при всех
1 , 2 ,..., n равных нулю.
28.
Свойства линейно зависимых и линейнонезависимых систем векторов
Теорема 2
Если в системе векторов имеется нулевой вектор, то система линейно
зависима.
Док-во:
Пусть a1 0, тогда 1 0, 2 3 ... n .0
Выразим 1a 0a 0a ... 0. a
1
2
3
n
По определению №20 система a1 , a2 ,..., an линейно зависима.
назад к содержанию
29.
Теорема 3Если в системе векторов имеется линейно зависимая подсистема, то и вся
система линейно зависима.
Док-во:
Пусть a1 , a2 ,..., ak - линейно зависимая система в системе a1 , a2 ,..., ak , ak 1 ,...,. an
1 , 2 ,..., k , среди которых хотя бы одно не равно нулю.
1a1 2 a2 ... k ak 0,
k n
Пусть k 1 k 2 ... n 0
1a1 2 a2 ... k ak 0 ak 1 0 ak 2 ... 0 an 0
Значит, по определению №19, система линейно зависима.
Теорема 4
Любая подсистема линейно независимой системы линейно независима.
Док-во: от противного
Пусть система векторов линейно независима, а в ней существует линейно
зависимая подсистема. По теореме №3, данная система векторов линейно
зависимая.
Получаем противоречие, так как по условию дана линейно не зависимая
система.
Значит, любая подсистема линейно независимой системы линейно
независима.
30.
Геометрический смысл линейнойзависимости и независимости векторов
Теорема 5
Векторы a и b линейно зависимы a // .b
Док-во:
(из определения №20)
a и b – линейно зависимы b a или
a // b (по теореме №1 о коллинеарных векторах).
Следствие 1 из Т5
Нулевой вектор коллениарен любому вектору
Док-во: вытекает из теоремы №2 и №5.
Следствие 2 из Т5
Для того чтобы два вектора были линейно независимы необходимо и
достаточно, чтобы b был не коллениарен a .
Док-во: необходимость и достаточность вытекают из теоремы №5 с помощью
доказательства «от противного».
a b
назад к содержанию
31.
Определение №22Три и более векторов называются компланарными, если эти векторы лежат в
одной или параллельных плоскостях.
Теорема 6
Для того чтобы система из трёх векторов была линейно зависима необходимо и
достаточно, чтобы эти векторы были компланарными.
Док-во:
Необходимость.
a, b, c- линейно зависимы один вектор можно представить в виде линейной
комбинации двух других (по определению №20). Пусть c a b
На векторах a, b строим параллелограмм.
a // a
b // b
По правилу параллелограмма c – диагональ параллелограмма со сторонами
a, b . Параллелограмм – плоская фигура стороны параллелограмма и его
диагональ лежат в одной плоскости a, b, c компланарны a , b, c
- компланарны.
32.
Достаточность.a, b, c - компланарны. Пусть среди них нет нулевых векторов и
коллинеарных пар.
Приложим три вектора к точке О. Получаем точки А, В, С. Из точки С проведем
прямые, параллельные векторам a и b . Получаем параллелограмм OA’CB’.
По правилу параллелограмма
.
OC OA` OB`
OA`// a : OA` a (по теореме №1 о коллинеарных векторах)
OB `// b : OB ` b (по теореме №1 о коллинеарных векторах)
OC с a b
a, b, c – линейно зависимы (по определению №20).
Если же среди векторов a, b, c имеется нулевой, то система этих векторов
линейно зависима по теореме №2.
Если среди a, b, c имеется пара коллинеарных векторов, то по теореме № 5
эти 2 вектора линейно зависимы. Значит по теореме №3 все 3 вектора
линейно зависимы.
рис. 11
33.
Следствие 1 из Т6Нулевой вектор компланарен любой паре векторов.
Следствие 2 из Т6
Для того чтобы векторы
a, b, c были линейно независимы необходимо и
достаточно, чтобы они были не компланарны.
Следствие 3 из Т6
Любой вектор плоскости можно представить в виде линейной комбинации
любых двух неколлинеарных векторов этой же плоскости.
34.
Теорема 7Любые 4 вектора в пространстве линейно зависимы.
Док-во: Даны вектора a, b, c, d . Рассмотрим 4 случая:
1) Если среди векторов есть нулевой вектор. Тогда система линейно
зависима по Теореме №2.
2) Если среди векторов имеется хотя бы 1 пара коллинеарных векторов.
Тогда система линейно зависима по теореме №5 и №3.
3) Если среди векторов имеется комплнарная тройка векторов. Тогда система
линейно зависима по теореме №6 и №3.
4) Если среди векторов нет нулевых векторов, коллинеарных пар и
компланарных троек.
Тогда приложим эти 4 вектора к точке О.
a OA, b OB , c OС , d OD .
Проведем плоскость через вектора a, b , затем плоскость через вектора b, c
и плоскость через вектора a, c. Затем проведем плоскости, проходящие
через точку D, параллельные парам векторов a, b ; b, c ; a, c . По линиям
пересечения плоскостей строим параллелепипед OB1D1C1A1B2DC2.
рис. 12
рис. 13
35.
Рассмотрим OC1D1B1 – параллелограмм по построению по правилупараллелограмма OD1 OB1 OC1.
Рассмотрим OD1DA1– параллелограмм (из свойства параллелепипеда)
OD1 OA1 OD d
d OD OA1 OB1 OC1.
OA1 || OA a существует : OA1 a по теореме №1.
OB1 || OB b существует : OB1 b по теореме №1.
OС1 || OС с существует : OС1 с по теореме №1.
d a b c
По определению №20 система векторов a, b, c, d линейно зависимая.
36.
Следствие 1 из Т7Суммой трёх некомпланарных векторов в пространстве, приведенных к
общему началу, является вектор, совпадающий с диагональю
параллелепипеда, построенного на этих трёх векторах, начало которого
совпадает с общим началом трех векторов.
Следствие 2 из Т7
Если в пространстве взять 3 некомпланарных вектора, то любой вектор этого
пространства можно разложить в линейную комбинацию этих трёх векторов.
Следствие 3 из Т7
Максимальное число линейно независимых векторов в пространстве равно 3.
Максимальное число линейно независимых векторов в пространстве
называется размерностью пространства.
Размерность плоскости – 2, размерность пространства – 3.
37. Базис на плоскости и в пространстве
Определение №23Базисом на плоскости (в пространстве) называется упорядоченная пара
(тройка) линейно независимых векторов плоскости (пространства) при
условии, что любой вектор плоскости (пространства) разлагается в
линейную комбинацию этих векторов.
Утверждение 2
Для плоскости (пространства) любая упорядоченная пара (тройка)
неколлинеарных (некомпланарных) векторов плоскости(пространства)
может быть взята в качестве базиса этой плоскости (пространства).
Док-во:
Для плоскости. По следствию №2 из теоремы №5, если a неколлинеарен
b они линейно независимы. По следствию №3 из теоремы №6 любой
вектор можно выразить через a и b .
По определению, a, b можно взять в качестве базиса.
Для пространства. По следствию №2 из теоремы №7 любой вектор
пространства можно выразить через некомпланарные вектора a, b, c . По
определению, эти вектора можно взять в качестве базиса.
назад к содержанию
38.
Замечание: понятие координат вектораДалее все рассуждения для пространства справедливы также и для
плоскости.
a, b, c - базис в пространстве
d a b c - разложение вектора d по базису
Определение № 24
Упорядоченный набор коэффициентов , , называется координатами
вектора d в базисе a, b, c , d , , , если d a b c .
a - первый вектор базиса
b - второй вектор базиса
c - третий вектор базиса
Итак, координаты вектора – это коэффициенты разложения вектора по базису.
39.
Теорема 8 (о единственности разложения по базису)Любой вектор разлагается по базису единственным образом.
Док-во: от противного.
Допустим d 1 a 1 b 1 c и d 2 a 2 b 2 c
1 a 1 b 1 c 2 a 2 b 2 c
(свойство вектора: возможность существования противоположного)
1 a 1 b 1 c 2 a 2 b 2 c 0
(коммутативность сложения, дистрибутивность относительно сложения
чисел) ( 1 2 )a ( 1 2 )b ( 1 2 )c 0.
a, b, c – система линейно независимых векторов, т. к. базис, и ее линейная
комбинация 0 (следовательно по определению №21 линейно
независимой системы) при всех коэффициентах равных 0
1 2 0, 1 2 0, 1 2 0 1 2 , 1 2 , 1 2
разложение единственно.
40.
Теорема 9 (о свойствах линейных операций над векторами)1) Соответствующие координаты равных векторов равны.
d 1 1 , 1 , 1 , d 2 2 , 2 , 2
d 1 d 2 1 2 , 1 2 , 1 2
2) При сложении двух векторов соответствующие координаты складываются.
d 1 d 2 1 2 ; 1 2 ; 1 2
3) При умножении вектора на число, его координаты умножаются на это
число.
d , , , R
Док-во:
1.
d 1 1 a 1 b 1 c и d 2 2 a 2 b 2 c (коммутативность сложения,
дистрибутивность относительно сложения чисел)
1 a 1 b 1 c 2 a 2 b 2 c ( 1 2 )a ( 1 2 )b ( 1 2 )c 0.
Линейная комбинация векторов 0 . a, b, c - система линейно независимых
векторов
1 2 0, 1 2 0, 1 2 0 1 2 , 1 2 , 1 2 .
41.
Достаточность1 a 1 b 1 c 2 a 2 b 2 c
( 1 2 )a ( 1 2 )b ( 1 2 )c 0
0a 0b 0c 0
2) d1 d 2 1 a 1 b 1 c 2 a 2 b 2 c
=(коммутативность сложения, дистрибутивность относительно сложения чисел)=
( 1 2 )a ( 1 2 )b ( 1 2 )c d1 d 2 1 2 ; 1 2 ; 1 2 .
3) d1 1 a 1 b 1 c =(дистрибутивность относительно сложения векторов)=
1 a 1 b 1 c =(ассоциативность)=
1 a 1 b 1 c d1 1; 1; 1 .
42.
Векторное пространствоОпределение №25.
Векторное пространство – произвольное множество элементов (векторов), на
котором введены операции: сложение элементов и умножение на число из
R; и удовлетворяющие 8 аксиомам:
1. Коммутативность сложения векторов
2. Ассоциативность сложения векторов
3. Существование нуля
4. Существование противоположного элемента
5. Дистрибутивность умножения вектора на число относительно сложения
векторов
6. Дистрибутивность умножения вектора на число относительно сложения
чисел
7. Ассоциативность умножения
8. Умножение на единицу
Примером векторных пространств могут служить:
1. плоскость – двумерное векторное пространство;
2. прямая – одномерное пространство;
3. множество всех многочленов от одной переменной до n-ой степени;
4. множество всех матриц- столбцов длины n;
5. Множество всех квадратных матриц n-го порядка;
6. Множество непрерывных функций, определенных на промежутке [0;1].
назад к содержанию
43.
Аффинная система координатОпределение №26
Координаты вектора – коэффициенты разложения данного вектора по базису.
Определение №27
АСК – совокупность базиса и точки, к которой приложены векторы базиса.
Oe1 , e2 , e3 ; О – точка, к которой приложены векторы базиса есть начало АСК.
Определение №28
Радиус-вектор точки М – это вектор, начало которого совпадает с началом
АСК, а конец – с т. М.
OM – радиус-вектор т. М
rm OM e1 e2 e3 , , – коэффициенты разложения по базису.
рис. 14
Определение №29
Координаты т. М в АСК Oe1 , e2 , e3 – координаты rm в базисе данной АСК.
M ( , , ) .
назад к содержанию
44.
Простейшие задачи в АСКНахождение координат вектора по данным начала и конца.
Найти координаты вектора с заданными началом и концом:
рис. 15
Дано:
A( A ; A ; A )
B( B ; B ; B )
AB rB rA
по правилу треугольника
В силу теоремы №9(2) получаем:
AB { B A ; B A ; B A }
Утверждение
b // a
b b b
a a a
назад к содержанию
45.
.Деление отрезка в данном отношении
Известны координаты т. А и В в некоторой АСК.
Дано: АСК; O, e1 , e2 , e3 ; A A ; A ; A ; B B ; B ; B
AM
MB
AM MB
Найти: m ; m ; m ?
AM MB
AM M A , M A , M A
MB B M , B M , B M
По теореме 9(3 и 1):
A B
M
1
M A ( B M )
B
AM MB M A ( B M ) M A
1
M A ( B M )
M A B
1
рис. 16
46.
Проекция вектора на осьОпределение №30
Рассмотрим прямую и вектор e на этой прямой. Этот вектор является базисом
любых векторов, лежащих на этой прямой.
рис. 17
Определение №31
Прямая с зафиксированным на ней ненулевым вектором называется осью(l – ось).
a l ; l , e ось, a a e ( a – координата вектора оси).
Определение №32
Ось с введенной АСК называется числовой осью.
Пусть заданы: ось l , прямая d e и т. М .
рис. 18
d // MM '
М` - проекция т. М на ось l вдоль прямой d ( на плоскости)
d не параллельна l.
рис. 19
назад к содержанию
47.
М` - проекция точки М на ось l вдоль плоскости(в пространстве)
На плоскости d l (в пространстве l ), то проекция т. М на ось l называется
ортогональной проекцией.
Определение №33
Проекцией вектора AB на ось l вдоль прямой d (плоскости ) называется вектор A' B '
, где А` - проекция т. А на ось l , а В` - проекция т. В на ось l вдоль прямой d
AB
(плоскости ) – векторная проекция на ось.
Определение №34
Координата вектора A' B ' на оси l называется числовой проекцией вектораAB на ось l
вдоль прямой d.
рис. 20
прd l AB.
48.
Свойства проекции:1) a b прi a прi b
2) прi (a b) прi a прi b
3) прi ( a ) прi a
4) прi a | a | cos
2) A' B' B' C ' A' C '
AB BC AC
A' C ' пр AC
d
i
прl a – ортогональная проекция вектора a на ось l
- угол наклона a к l.
Док-во:
49.
4) Расмотрим треугольник ACB – прямоугольный.AC A' B'
AC AB cos .
Знак – или + зависит от угла φ: Если φ острый, то +, если φ тупой, то –.
AC прl AB
прl ' AB AB cos
прl ' AB прl AB AC A' B '
A' B ' прl AB AB cos .
рис. 22
50.
Прямоугольная декартова системакоординат (ПДСК)
Определение №35
Прямоугольная декартова система координат (ПДСК) – это АСК, у которой углы
между двумя любыми базисными векторами прямые и модули базисных
векторов равны.
За единицу длины принимается длина базисного вектора.
Базис в ПДСК при этом называется ортонормированным.
i, j , k - орты ПДСК (базисные векторы).
назад к содержанию
51.
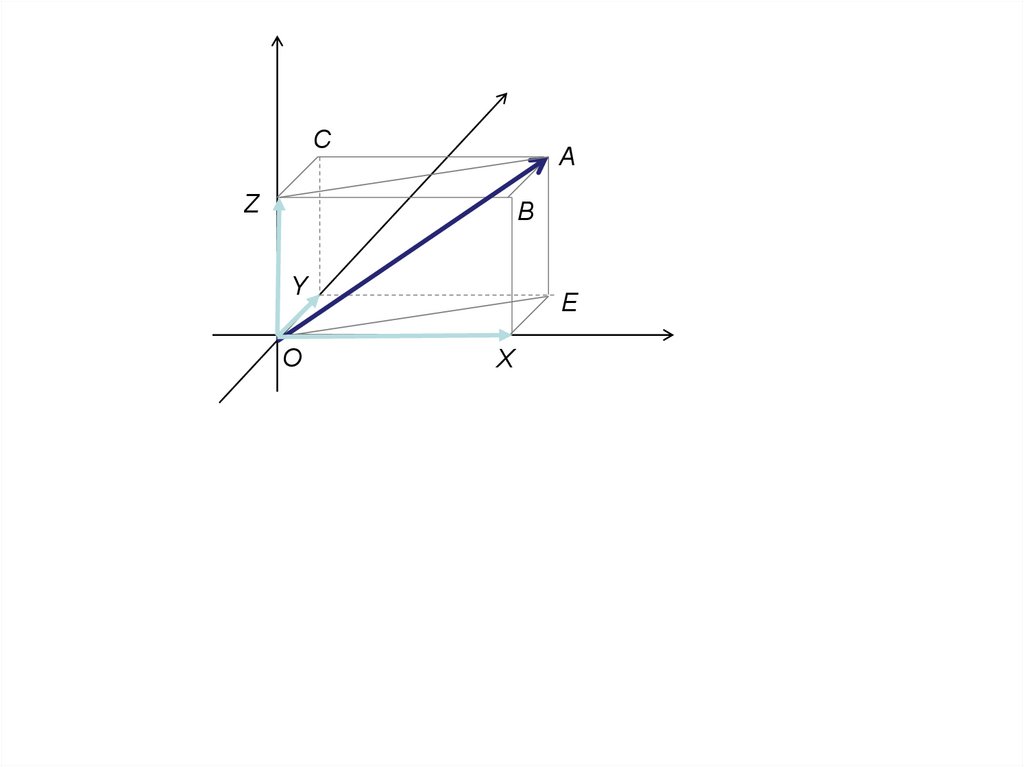
Рассмотрим ПДСК. Отложим вектор a от начала координат. На осях координатпостроим параллелепипед, диагональ которого совпадает с вектором a .
рис. 23
Полученный параллелепипед OXEYZBAC – прямоугольный по построению.
OA OX OY OZ (по следствию №1 из теоремы №7).
OX // i (по теореме №1) x : OX xi,аналогично , OY y j , OZ z k .
x OX , y OY , z OZ .
2
2
2
a OE OZ , так как OEAZ – прямоугольник;
2
2
2
2
2
2
OE OX OY , так как OXEY – прямоугольник.
2
OA OX OY OZ ,
.2
a x2 y2 z2 a x2 y2 z2 .
Мы доказали утверждение.
Утверждение №3
Если a {x;y;z} в ПДСК, то
a x2 y2 z 2 .
52.
CА
Z
B
Y
О
E
Х
53.
Теорема 10Координаты вектора в ПДСК равны ортогональным проекциям этого вектора на
соответствующие оси координат.
Док-во:
Приложим вектор aк началу координат и построим параллелепипед на осях
координат. Тогда OX– ортогональная векторная проекция вектора
на ось
a x.
x –OX
координата
i
xi . на оси x в базисе .
По определению: x – числовое значение проекции вектора
на a
ось x.
Так
x
прi a.
как плоскости взаимно перпендикулярны и перпендикулярны осям, аналогично
y пр j a, z прk a.
рис. 23
a xi y j z k
Теорема 10’
Первая координата вектора
в АСК равна проекции вектора
на ось
вдоль плоскости, параллельной
. Вторая координата
e1 в
a векторам
a вектора
АСК равна проекции вектора
на ось
плоскости, параллельной
eвдоль
2 , e3
векторам
. Третья координата
вектора
e2 в АСК равна проекции вектора
a
на ось
eвдоль
, e плоскости, параллельной векторам
a
e3
1
3
e2 , e1.
54.
Длина вектора. Расстояние между двумяточками в ПДСК
a x ; y ; z
В силу утверждения №3
2
a x2 y 2 z 2
M1 ( x1 ; y1 ; z1 ) ; M 2 ( x2 ; y2 ; z2 )
В силу того же утверждения №3
d M1M 2 | M1M 2 | ( x2 x1 )2 ( y2 y1 )2 ( z2 z1 )2
d M M - расстояние между M и M .
2
1
1
(1)
2
Направляющие косинусы вектора
Пусть α – угол наклона вектора a к оси х.
β – угол наклона вектора a к оси y.
γ – угол наклона вектора a к оси z.
По теореме №10 и свойству 4 проекции мы получаем выражение координат вектора
через его длину и направляющие косинусы:
x прi a | a | cos
(2)
y пр j a | a | cos
рис. 24
z пр k a | a | cos
назад к содержанию
55.
Определение №37cos , cos , cos – направляющие косинусы вектора . a
Подставим эти преобразования в равенство
| a |2 x 2 y 2 z 2
| a |2 | a |2 cos 2 | a |2 cos 2 | a |2 cos 2
cos 2 cos 2 cos 2 1 - условие на направляющие косинусы
Из формулы выражения координат вектора через его длину и направляющие косинусы
мы получаем:
cos
cos
cos
x
|a|
y
|a|
z
|a|
x
x2 y2 z2
y
x2 y2 z2
z
x2 y2 z2
(3)
56.
Скалярное произведение векторовОпределение №38
Скалярным произведением вектора
a на b называется число, равное ^
произведению модулей этих векторов на косинус угла между ними a b .
(4)
a b | a | | b | cos
Определение №39
Угол между векторами a и b – это наименьший угол между векторами a и b ,
приведенными к общему началу.
- угол между a и b, 0; .
Проекция вектора a на направление вектора b, т. е. проекция вектора a на
ось, связанную с b . прb a | a | cos .
рис. 25
(4’)
a b | b | пр a | a | пр b
b
a
назад к содержанию
57.
Геометрические свойства скалярногопроизведения
Теорема 11 (О геометрических свойствах скалярного произведения)
a , b 0
a , b 0
2) a b 0 острый
a b 0 тупой
a , b 0
Док-во:
1)
a b a b 0
1)a b 0 | a | | b | cos 0 cos 0 90 a b
2)a b 0 | a | | b | cos 0 cos 0 0; острый
2
a b 0 | a | | b | cos 0 cos 0 ; тупой
2
Замечание
cos
a b
| a | |b|
(5)
назад к содержанию
58.
Алгебраические свойства скалярногопроизведения
1) a b b a
коммутативность
2) a(b c) a b a c дистрибутивность
3) ( a )b (ab) ассоциативность относительно умножения на число
2
2
2
4) a a a | a | 2 , a 0, a 0 a 0
Док-во:
1) a b | a | | b | cos | a | | b | cos( a ^ b) | b | | a | cos(b^ a )
| b | | a | cos b a.
(по свойству проекции)
2) a (b c ) | a | прa (b c )
| a | ( прa b прa c ) | a | прa b | a | прa c a b a c
3) ( a ) b | b | прb a (по
свойству проекции)
| b | прb a ( a b)
4) a a | a | | a | cos 0 | a |2 , a 2 0 | a | 0 a 0
назад к содержанию
59.
Скалярное произведение в координатахТеорема 12
Пусть в ПДСК заданы координаты векторов a, b : a x1 , y1 , z1 , b x2 , y2 , z 2 .
Скалярное произведение двух векторов в координатах есть сумма
произведений соответствующих координат. a b x x y y z z .
(6)
1 2
1 2
1 2
Док-во:
a x1 i y1 j z1 k ,
b x2 i y 2 j z 2 k ,
i j i j cos 90 0, (так как векторы взаимно перпендикулярны)
i j j k k i 0,
2
2
2
i
j
k
1
(Из свойств скалярного произведения и перпендикулярности векторов)
a b x1 i y1 j z1 k x2 i y2 j z 2 k
2
2
x1 x2 i x1 y2 i j x1 z 2 i k y1 x2 j i y1 y2 j y1 z 2 j k z1 x2 k i z1 y2 k j
2
z1 z 2 k x1 x2 y1 y2 z1 z 2 .
назад к содержанию
60.
Теорема 12’Пусть в АСК заданы координаты векторов
a x1 e1 x2 e2 x3 e3 x1 ; x2 ; x3 ,
b y1 e1 y2 e2 y3 e3 y1 ; y2 ; y3 .
Тогда a b i3, j 1 xi y j gij ,
gij ei e j .
Следствие 1 из Т12
Пусть в ПДСК заданы координаты векторов a, b : a x1 , y1 , z1 , b x2 , y2 , z 2 .
Тогда 1)a b x1 x2 y1 y2 z1 z2 0,
^
2) a b
^
острый x x
3) a b
Следствие 2 из Т12
1 2 y1 y2 z1 z2 0,
тупой x x
1 2 y1 y2 z1 z2 0.
cos( a b)
a b
| a | |b|
Следствие 3 из Т12
x1x2 y1 y2 z1z2
x1 y1 z1 x2 y2 z2
2
2
2
2
2
(7)
| a | a a x1x1 y1 y1 z1z1 x1 y1 z1
(8)
a b x1 x2 y1 y2 z1z2
b
x 2 y 2 z 2
(9)
2
Следствие 4 из Т12
2
прb a
2
2
2
2
2
61.
Векторное произведение векторовОпределение №40
Три вектора a, b, c называется упорядоченной тройкой, если каждому из
них присвоен номер.
Определение №41
Упорядоченная тройка некомпланарных векторов называется правой или
тройкой положительной ориентации, если выполнены условия: если будучи
приведенными к общему началу, векторы упорядоченной тройки
расположены так, как можно расположить пальцы правой руки, т. е. первый
вектор по направлению большого пальца, второй – по направлению
указательного, третий – по направлению среднего (для левой руки тройка
будет левой).
Определение №42
Упорядоченная тройка векторов называется правой, если выполнены
условия: если находиться в растворе трёхгранного угла тройки векторов,
приведённых к общему началу, и мысленно вращать от 1-го ко 2-му , от 2-го к
3-му, от 3-го к 1-му , то вращение будет против часовой стрелки ; тройка
векторов левая, если вращение по часовой стрелке.
назад к содержанию
62.
Определение №43Если смотреть на упорядоченную тройку векторов, приведённую к общему
началу, из конца 3-го вектора и вращать 1-ый и 2-ой вокруг третьего в
направлении от 1-го ко 2-му, то вращение против часовой стрелки говорит о
том, что тройка правая а по часовой – левая.
Определение №44
Перестановка векторов упорядоченной тройки называется циклической,
если 1-ый вектор ставится на последнее место, а номера остальных
векторов уменьшаются на один(последний вектор ставится на 1-е место, а
остальные номера увеличиваются на один).
63.
Лемма №1Если в упорядоченной тройке векторов выполнить циклическую перестановку
векторов, то ориентация тройки не изменится.
Док-во: (на основе второго определения упорядоченной тройки)
рис. 26
Лемма №2
Если поменять номера 2-ух векторов упорядоченной тройки, то ориентация
тройки изменится на противоположную.
Док-во:
рис. 27
64.
Лемма №3Даны векторы a , b , c , d ; c || d ,
a , b , c и a , b , d некомпланарные
тройки. Если тройки a , b , c и a , b , d имеют одинаковые ориентации,
то c d ; если a , b , c и a , b , d имеют различные ориентации, то c d .
И наоборот.
Определение №45
Векторным произведением векторов a , b называется вектор
с a ; b a b a b , для которого выполнены следующие условия:
1) | c | a ; b | a | | b | sin a ^ b
2) c a , b
3)c направлен так, что тройка a , b , c имеет ориентацию базиса; если
базис правый, то a , b , c правая тройка; если базис левый, то a , b , c
левая тройка.
65.
Геометрические свойства векторногопроизведения
Теорема 13
1)Площадь параллелограмма, построенного на векторах
a ,, b
приведённых к общему началу, равна модулю их векторного произведения.
S ab a , b
2)a || b a , b 0
Док-во:
1)Построим параллелограмм на векторах a , b . Sab | a || b | sin( a^ b) (по
определению векторного произведения) | [a, b] | .
2)Необходимость.
a || b Угол между векторами 0 или . sin( a ^ b) 0 | [a; b] | 0 [a; b] 0
Достаточность.
[a; b] 0 a b sin( a ^ b) 0 a 0 или b 0 или sin( a ^ b) 0 a // b .
назад к содержанию
66.
Алгебраические свойства векторногопроизведения
1)[ a; b] [b; a ] антикоммутативность,
2)[ a; b] [a; b] [a; b] ассоциативность относительно умножения на
число,
3)[a; a ] 0 ,
4)[ a; b] [a'; b]
где
a' векторная проекция a на прямую перпенди-
кулярную b и лежащую в плоскости векторов a и b ,
5)[ a; b c] [a; b] [a; c] дистрибутивность.
назад к содержанию
67.
Док-во свойств: 1.[ a; b] a b sin a; b
[ a; b] [ b; a ]
[ b; a ] b a sin b; a
[ a; b] a; b
[ a; b] || [ b; a ]
[ b; a ] b; a
a; b; [ a; b] правая тройка (по определению)
b; a; [ b; a ] правая тройка (по определению)
a; b; [ b; a ] левая тройка (по лемме №2)
По лемме №3 [ a; b]
[ b; a ] [ a; b] [ b; a ].
68.
2.[ a; b] a b sin a; b ,
a; b ,
1) 0 a; b ,
2) 0 a; b ,
sin sin( ),
a b sin a; b a b sin a; b ,
получили, что модули равны
[ a; b] a ; b [ a; b] a; b,
[a; b] a; b [ a; b] || [a; b].
1) 0 a; b; a; b правая тройка
a ; b ; [ a; b] правая тройка, т.к.
a a
a ; b ; [a; b] правая тройка a ; b ; [a; b] правая тройка, т.к. [a ; b] [a ; b].
Тогда по лемме №3: [ a ; b] [ a ; b].
69.
2) 0 a; b; a; b правая тройкаa ; b ; [ a; b] левая тройка, т.к. 0
a ; b ; [a; b] правая тройка, a ; b ; [a; b] левая тройка.
Тогда по лемме №3: [ a ; b] [ a ; b].
3. Доказать самостоятельно
4.
[a; b] a b sin a; b ,
[a ' ; b] a ' b sin 90 a ' b ,
a ' a cos 90 a sin ,
[a ' ; b] a ' b sin [a; b] [a ' ; b] ,
a ; b [ a; b]
[a; b] || [a ' ; b],
a ' ; b [a '; b]
a ; b ; [a; b] правая тройка,
a ' ; b ; [a '; b] правая тройка,
a ; b ; [a '; b] правая тройка. Тогда по лемме №3: [a ; b] [a`; b].
рис. 28
70.
5.[ a , b c ] a ; b a ; c ,
b c ' b` c`,
a , b` a , b ,
a , c` a , c ,
[ a , b` c` ] [ a , b c ],
Повернём параллелограмм в плоскости
на
90 смотреть из конца вектора
; если
, то противaчасовой стрелки. Каждый вектор умножаем на
| a |.
b`` b` a , c`` a c`,
b`` c`` b` c` a ,
b` c` ' b`` c``,
b`` [ a , b` ],
b`` a b` ,
a , b` a b` sin 90 a b` ,
рис. 28
71.
a ; b` a , b`(по опр. векторного произведения) a ; b` || b``,b`` a , b`
a , b`, a ; b`
a , b` , b`` ( праваятройка по построению вектора b`` )
[a ; b`] b``,
b`` [ a ; b` ] ; c`` [ a ; c` ] ; ( b` c`) [ a ; b` c` ]
В силу того, что (b` c`)` b`` c``,
a; b` c` a; b a; c` a; b c a; b a; c .
72.
Векторное произведение в координатахТеорема 14
Пусть в ПДСК заданы векторы a x1 , y1 , z1 , b x2 , y2 , z 2 .
y1
Тогда: a; b
y2
z1 x1
;
z 2 x2
z1 x1
;
z 2 x2
y1
.
y2
Док-во:
a x1 , y1 , z1 x1 i y1 j z1 k .
Рассмотрим i; j .. Докажем, что i; j k .
i; j i j sin 90 1, k 1 длины векторов равны.
i; j i, j(по определению векторного произведения), а k i, j (так как
базисные векторы в ПДСК) k || i; j .
Причем i, j , k – правая тройка векторов и i, j , i; j правая тройка векторов
(по определению). По лемме №3 k i; j .
Значит i; j k .
Аналогично доказывается, что j; k i, k ; i j.
В силу антикоммутативности векторного произведения
j; i k , k ; j i, i; k j.
назад к содержанию
73.
В силу свойства 3 векторного произведенияi; i j; j k ; k 0.
Мы доказали следующую таблицу.
Таблица векторных произведений
[ i , i] 0 ; [ i , j] k ; [ i , k ] j
[ j , i ] k ; [ j , j ] 0 ; [ j , k ] i
[ k , i ] j ; [ k , j ] i ; [ k , k ] 0
74.
Используя свойства векторного произведения (дистрибутивность,ассоциативность умножения вектора на число) и таблицу векторных
произведений вычислим
a; b x1i y1 j z1 k ; x2 i y2 j z2 k x1x2 [ i , i ] x1 y2 [ i , j ] x1z2 [ i , k ]
y1 x2 [ j , i ] y1 y2 [ j , j ] y1 z2 [ j , k ] z1 x2 [ k , i ] z1 y2 [ k , j ] z1 z2 [ k , k ]
x1 y2 k x1 z2 j y1 x2 k y1 z2 i z1 x2 j z1 y2 i
i y1 z2 z1 y2 j x1 z2 z1 x2 k x1 y2 y1 x2
y z1
x z1
x
y1 y1 z1 x1 z1 x1 y1
i 1
j 1
k 1
;
;
.
y 2 z2
x2 z 2
x2 y 2 y 2 z 2 x2 z 2 x2 y 2
i
j k
a; b x1 y1 z1 .
x2 y 2 z 2
75.
Следствие из Т14a // b [a; b] 0
y1 z1
x z
x y
0 ; 1 1 0 ; 1 1 0
y2 z 2
x2 z2
x2 y2
y1 z 2 y2 z1 0
a // b x1 z 2 x2 z1 0
x y x y 0
1 2 2 1
a || b
Разделим на
Разделим на
Разделим на
y1 z1
y2 z 2
y2 z 2
z
x
y
z
x
x2 z 2 1 1 1 1 1
x2 y 2 z 2
x2 z 2
x2 y 2
x1 y1
x
2 y2
x1 y1 z1
x2 y2 z 2 пропорциональность соответствующих координат.
76.
Применение векторного произведенияПусть даны в ПДСК координаты векторов a x1 , y1 , z1 , b x2 , y2 , z 2 .
Sab a; b
ha
Sab
|a |
sin( a ; b)
y1 z1 2 x1 z1 2 x1 y1 2
y2 z2
x2 z 2
x2 y 2
y1 z1 2 x1 z1 2 x1 y1 2
y 2 z2
x2 z 2
x2 y 2
рис. 29
x12 y12 z12
| [ a ; b] |
| a || b |
y1 z1 2 x1 z1 2 x1 y1 2
y 2 z2
x2 z 2
x2 y 2
x12 y12 z12 x2 2 y2 2 z2 2
a x1 , y1 ,0 x1 , y1
b x2 , y2 ,0 x2 , y2
Sab
x1 y1 2
x y
mod 1 1 ;
x2 y 2
x2 y 2
S
1
1
x y
Sab mod 1 1
x2 y 2
2
2
назад к содержанию
77.
A x A , y A1
xB x A yB y A
, где B x B , y B
S ABC mod
y
y
x
x
2
A
C
A
C
C x , y
AB x B x A ; y B y A
AC xC x A ; yC y A
a x1 e1 y1 e2 z1 e3
b x2 e1 y2 e2 z2 e3
C
C
[a; b] [ x1 e1 y1 e2 z1 e3 ; x2 e1 y2 e2 z2 e3 ]
x1 y2 [e1 ; e2 ] x1 z2 [e1 ; e3 ] y1 x2 [e2 ; e1 ] y1 z2 [e2 ; e3 ] z1 x2 [e3 ; e1 ] z1 y2 [e3 ; e2 ]
yz
xz
xy
1 1 [e1 ; e2 ] 1 1 [e1 ; e3 ] 1 1 [e2 ; e3 ]
y 2 z2
x2 z 2
x2 y 2
78.
Смешанное произведение векторовОпределение №46
Смешанным произведением векторов a , b , c называется скалярное
произведение векторного произведения a , b на вектор c .
a , b c
Геометрический смысл смешанного
произведения
Теорема 15
Смешанное произведение некомпланарных векторов a , b , c равно
объёму параллелепипеда, построенного на этих векторах, приведенных к
общему началу, взятому со знаком «+», если тройка векторов a , b , c
правая, и со знаком «-», если тройка левая.
Смешанное произведение векторов a , b , c равно 0, тогда и только тогда
когда векторы компланарны.
назад к содержанию
79.
Док-во:1)Рассмотрим a и b. eab
и по определению).
a; b .
a; b
a, b , eab правая тройка (так как eab a; b
a; b c a; b пр. c (по теореме №13) S H V
eab
ab
ab
abc
Если a , b , c – правая тройка, то пр. c H ab (вектор c направлен в то же
eab
полупространство, что и eab , относительно плоскости a, b ).
Если a , b , c – левая тройка, то пр.e c H ab (вектора c и eab направлены
ab
в разные полупространства относительно плоскости a, b ).
2) a , b , c – компланарны Vabc 0 a; b c 0.
Vabc Sоснования H Sоснования 0 или H 0 векторы компланарны.
Замечание
В формулировке теоремы предполагается, что базис правый; если ориентация
базиса может быть любой, то соответствующие слова заменяем на: взятого со
знаком “+”, если ориентация базиса и тройки совпадают, и со знаком “-“ , если
ориентация тройки и базиса различны.
80.
Алгебраические свойства смешанногопроизведения
1.[ a , b] c a [ b; c ] a b c ( a b c )
2. a b c b c a c a b
3.a b c b a c c b a a c b
4.a a b a b b c b c 0
5.( a d )b c a b c d b c
6.( a ) b c ( a b c )
назад к содержанию
81.
1.[ a , b] c a [ b; c] a b c ( a b c)Док-во:
1.[ a , b] c [ b; c]a Vabc в силу теоремы №15.
Знак зависит от ориентации тройки b, c, a . При циклической
перестановке по лемме №1 ориентация тройки не меняется
a, b, c и b, c, a имеют одинаковую ориентацию.
В силу теоремы №15 a [ b; c] [ b; c] a имеют одинаковые знаки, так как
они равны по модулю a [ b; c] [ b; c] a a b c b c a a b c .
2. a b c b c a c a b
Док-во:
Вытекает из предыдущего свойства и леммы №1.
82.
3.a b c b a c c b a a c bДок-во:
a b c b a c c b a a c b Vabc
В силу леммы №2, если любые 2 вектора поменять местами, то ориентация
тройки изменится на противоположную.
То есть
c, b, a и b, a, c и a, c, b имеют ориентацию, противоположную
a, b, c.
В силу теоремы №15 у этих троек знак смешанного произведения
противоположен знаку тройки a, b, c. Значит a b c b a c c b a a c b.
4.a a b a b b c b c
Док-во:
3 вектора, два из которых равны, являются компланарными. Значит, по
теореме №15 их произведения равны 0.
83.
5.( a d )b c a b c d b ca d b; c (дистрибутивность скалярного произведения)
a b; c d b; c a b c d b c.
6.( a) b c (a b c)
Док-во:
Из ассоциативности скалярного произведения относительно умножения на
число.
84.
Смешанное произведение в координатахТеорема 16
Пусть в ПДСК даны координаты векторов:
a x1 , y1 , z1 , b x2 , y2 , z2 , c {x3 ; y3 ; z3}.
Смешанное произведение векторов a , b, c, координаты которого заданы в
ПДСК, находятся по формуле
Док-во:
Пусть a b с [ a; b] с.
y
По теореме №14 a; b 1
y2
x1
Разложим определитель x2
x3
x1
a b с x2
x3
z1 x1
;
z 2 x2
y1
y2
y3
y1
y2
y3
z1
z2 .
z3
z1 x1
;
z 2 x2
y1
.
y2
z1
z2 x3 A31 y3 A32 z3 A33.
z3
назад к содержанию
85.
Aij ( 1)i j M ij ,A31 ( 1)
3 1
A32 ( 1)
y1
M 31
y2
3 2
x1
M 32
x2
z1
,
z2
x1
x2
y1
,
y2
A33 ( 1)3 3 M 33
x1
x2
x3
y1
y2
y3
z1
,
z2
z1
y1
z 2 x3
y2
z3
z1
x1
y3
z2
x2
z1
x1
z3
z2
x2
y1
.
y2
86.
Следствие из Т16Необходимым и достаточным условием компланарности векторов
является: x
y z
1
1
x2
x3
y2
y3
a ,b,c
1
z2 0
z3
Теорема 16’
Пусть в АСК e1 , e2 , e3 даны координаты векторов
a 1 , 1 , 1 , b 2 , 2 , 2 , c 3 , 3 , 3 .
Смешанное произведение векторов
a , b , c, координаты которого заданы в
ПДСК, находятся по формуле
1
a b c 2
3
1 1
2 2 e1 e2 e3 .
3 3
87.
Применение смешанного произведенияНеобходимо найти характеристики различных геометрических фигур, если
известны координаты векторов, составляющих рёбра этих фигур (параллелепипед, пирамида).
Даны координаты векторов, составляющих рёбра выходящих из одной точки:
a x1 , y1 , z1 , b x2 , y2 , z2 , c {x3 ; y3 ; z3}.
x1 y1 z1
Vabc mod x2 y2 z2 ,
x3 y 3 z 3
1
Vтетр Vabc ,
6
x1 y1 z1
1
Vтетр mod x2 y2 z2 ,
6
x3 y 3 z 3
A( x A ; y A ; z A ),
B( x B ; y B ; z B ),
C ( xC ; yC ; zC ),
V ABCD ?
D( x D ; y D ; z D ),
назад к содержанию
88.
AB {xB x A ; y B y A ; z B z A }AC {xC x A ; yC y A ; zC z A }
AD {xD x A ; y D y A ; z D z A }
xB x A y B y A z B z A
1
1
VABCD VAB AC AD mod xC x A yC y A zC z A
6
6
xD x A y D y A z D z A
H ab ?
x1 y1 z1
mod x2 y2 z 2
H ab
Vabc
S ab
x3 y3 z3
y1 z1
y2 z 2
2
x1 z1
x2 z 2
2
x1 y1
x2 y 2
2
– формула нахождения высоты
параллелепипеда, построенного на
векторах a, b, c..
89.
Двойное векторное произведениеОпределение №47
Двойное векторное произведение есть вектор равный:
Теорема 17
a ;[b ; c] .
a ;[b ; c] b (a c) c (a b)
Док-во:
На основе теоремы №9 можно сделать вывод: если соответствующие координаты
векторов равны в каком-либо базисе, то векторы равны.
Выберем ПДСК:
Пусть Ox вдоль вектора b , тогда
b x1 ;0;0 .
Пусть Oy в плоскости векторов b и c , тогда
c x2 ; y2 ;0 .
a x3 , y3 , z3
0 0 x1 0 x1 0
[b ; c]
;
;
0;0; x1 y2 .
y 2 0 x2 0 x2 y 2
y3
z3
x3
z3 x3 y3
a; [b ; c]
;
;
x1 y2 y3 ; x1 y2 x3 ;0 .
0 x1 y2 0 x1 y2 0 0
назад к содержанию
назад к содержанию
90.
a c x2 x3 y2 y3 ,c a b x x x ; x x y ;0 ,
b a c c a b x y y ; x x y ;0 .
Векторное произведение
b a c x1 x2 x3 x1 y2 y3 ;0;0 ,
1
2
3
1 3
2
1
2
3
1 3
2
a b x1 x3 .











































































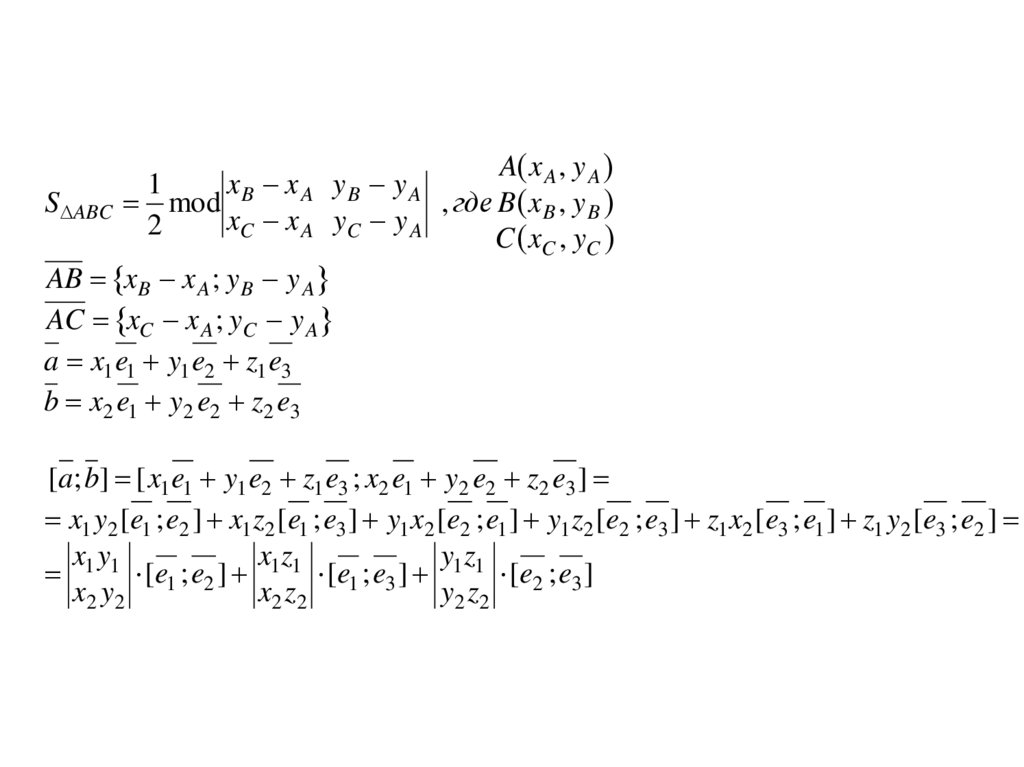







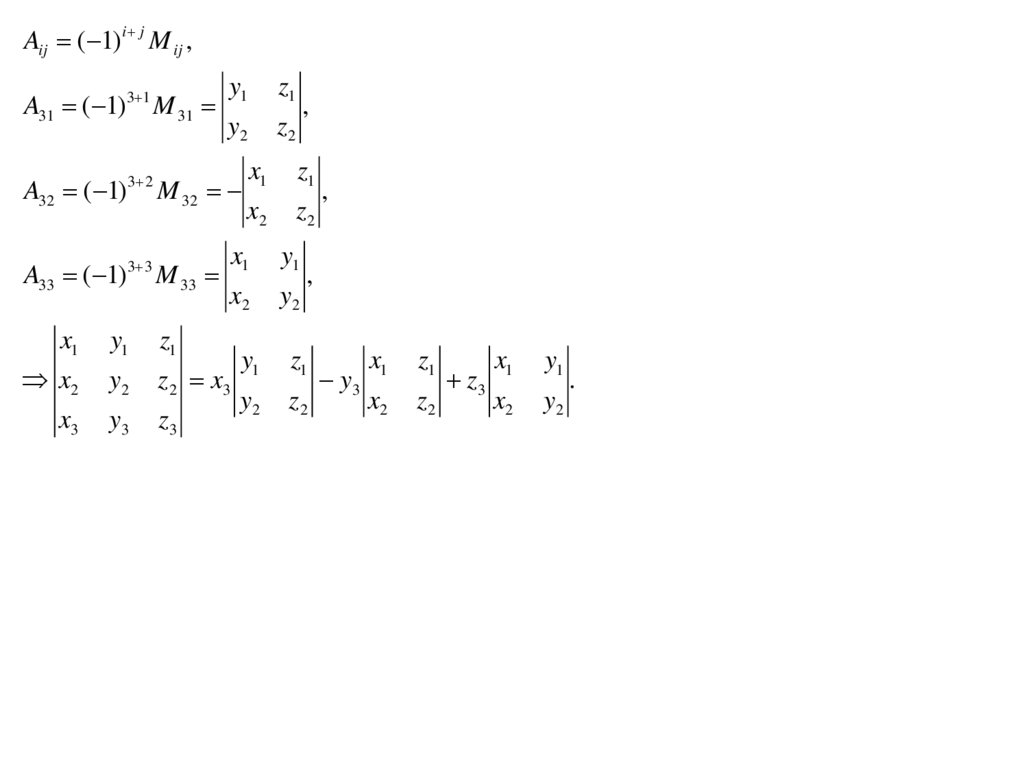





 mathematics
mathematics








