Векторная алгебра

1. Векторная алгебра

1

2. Основные понятия

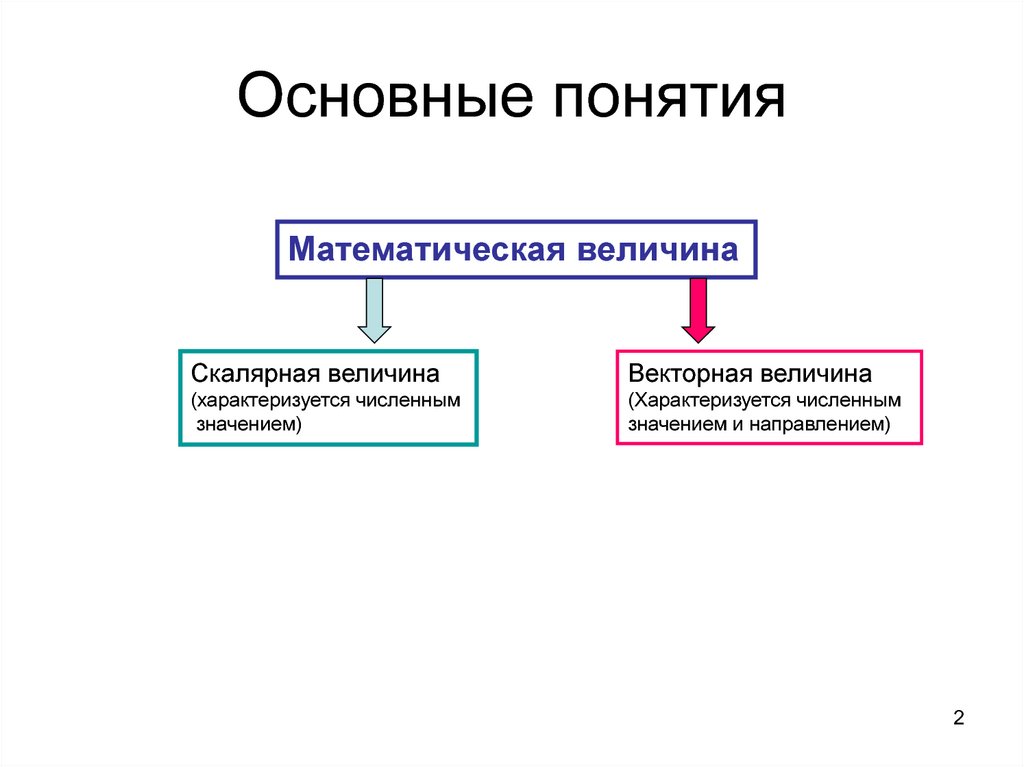
Математическая величина
Скалярная величина
Векторная величина
(характеризуется численным
значением)
(Характеризуется численным
значением и направлением)
2

3. Основные понятия

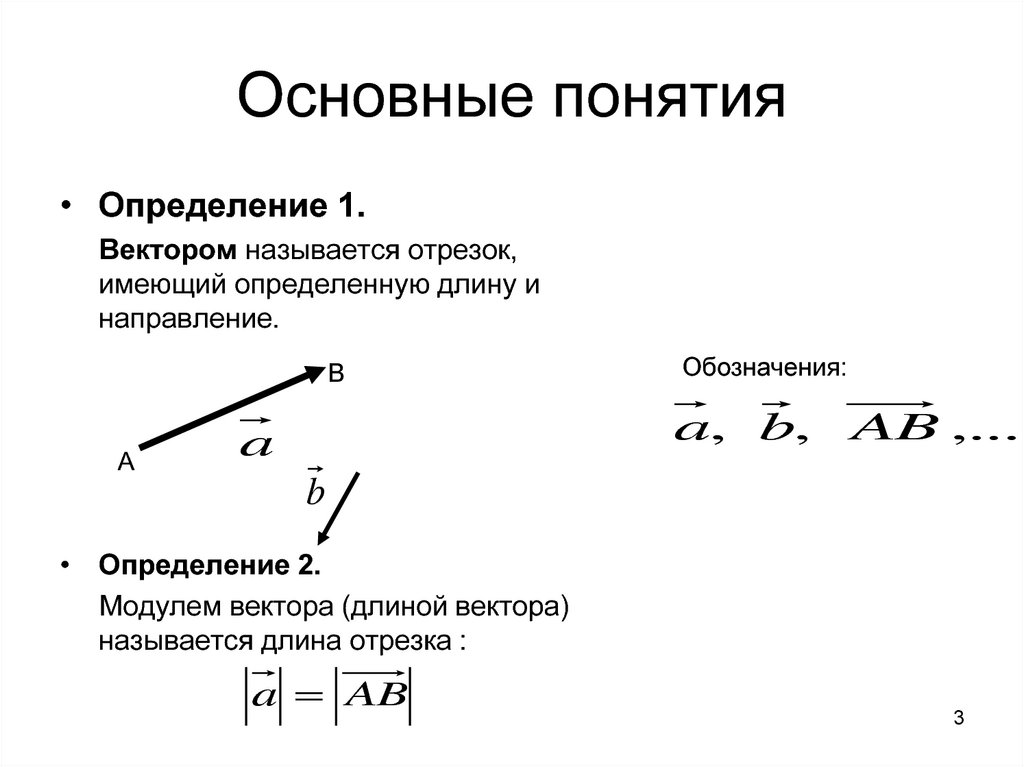
• Определение 1.
Вектором называется отрезок,
имеющий определенную длину и
направление.
В
А
Обозначения:
a, b,
a
AB ,...
b
• Определение 2.
Модулем вектора (длиной вектора)
называется длина отрезка :
a AB
3

4. Основные понятия

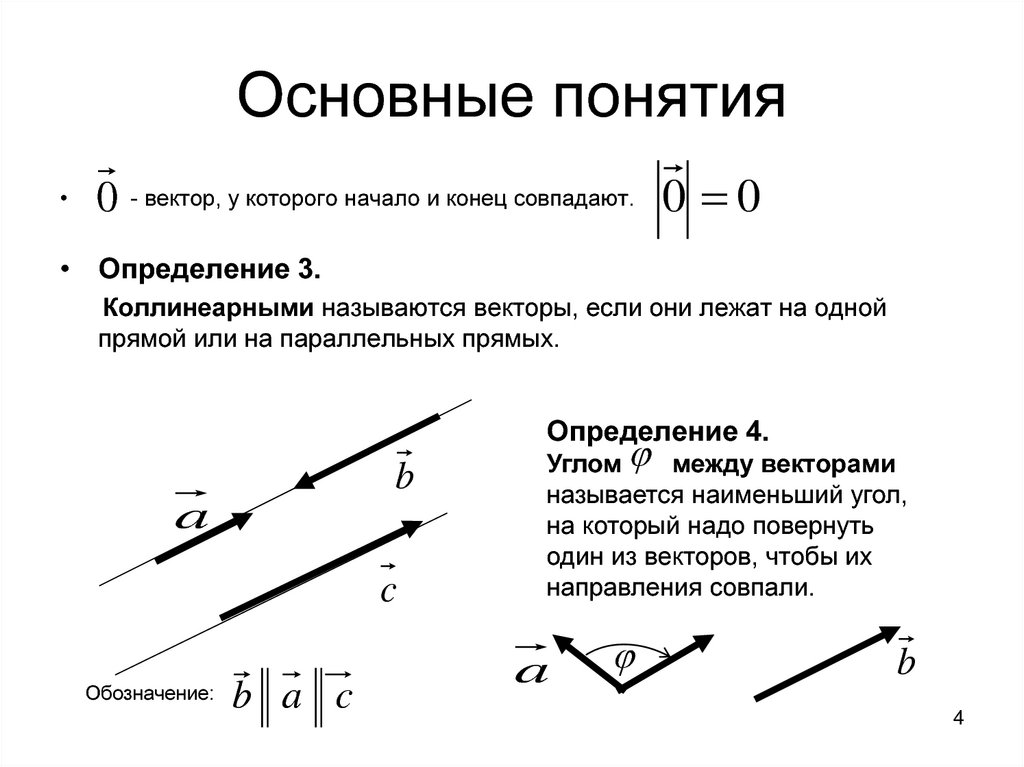
0 - вектор, у которого начало и конец совпадают. 0 0
• Определение 3.
Коллинеарными называются векторы, если они лежат на одной
прямой или на параллельных прямых.
Определение 4.
b
a
c
Обозначение:
b a c
Углом между векторами
называется наименьший угол,
на который надо повернуть
один из векторов, чтобы их
направления совпали.
a
b
4

5. Основные понятия

• Определение 5.
Два вектора называются равными, если
они коллинеарные, имеют одинаковую длину
и одинаковое направление.
a
b
a b
Следствие.
При параллельном переносе получаются равные векторы.
5

6. Основные понятия

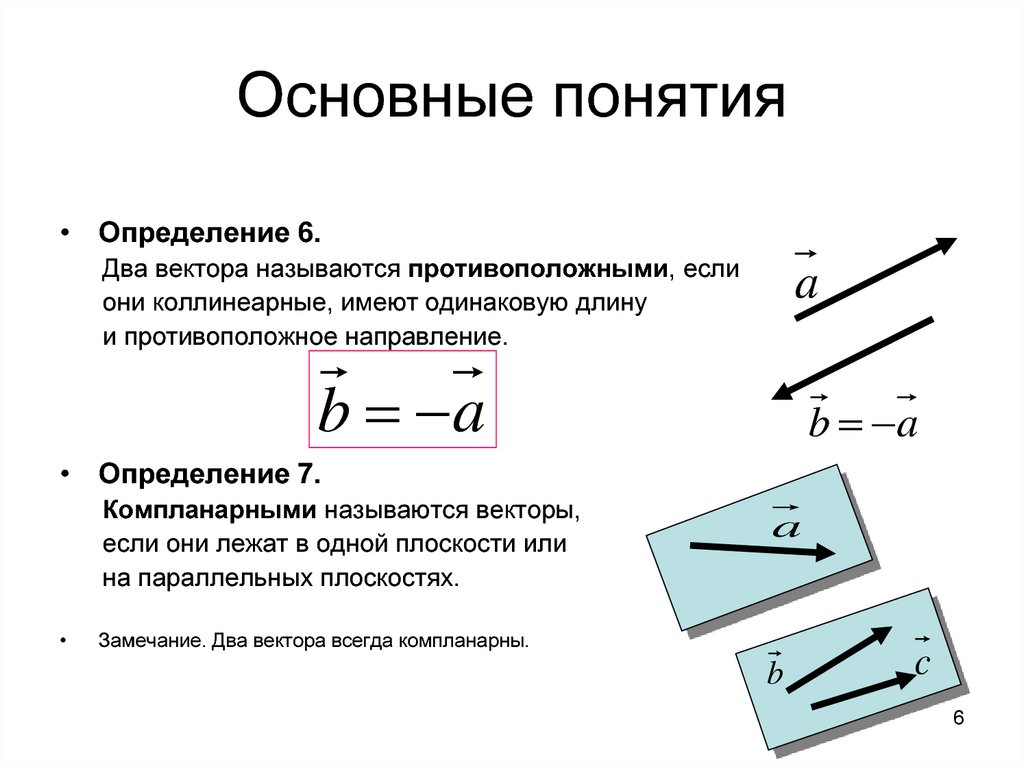
• Определение 6.
Два вектора называются противоположными, если
они коллинеарные, имеют одинаковую длину
и противоположное направление.
a
b a
b a
• Определение 7.
Компланарными называются векторы,
если они лежат в одной плоскости или
на параллельных плоскостях.
a
Замечание. Два вектора всегда компланарны.
b
c
6

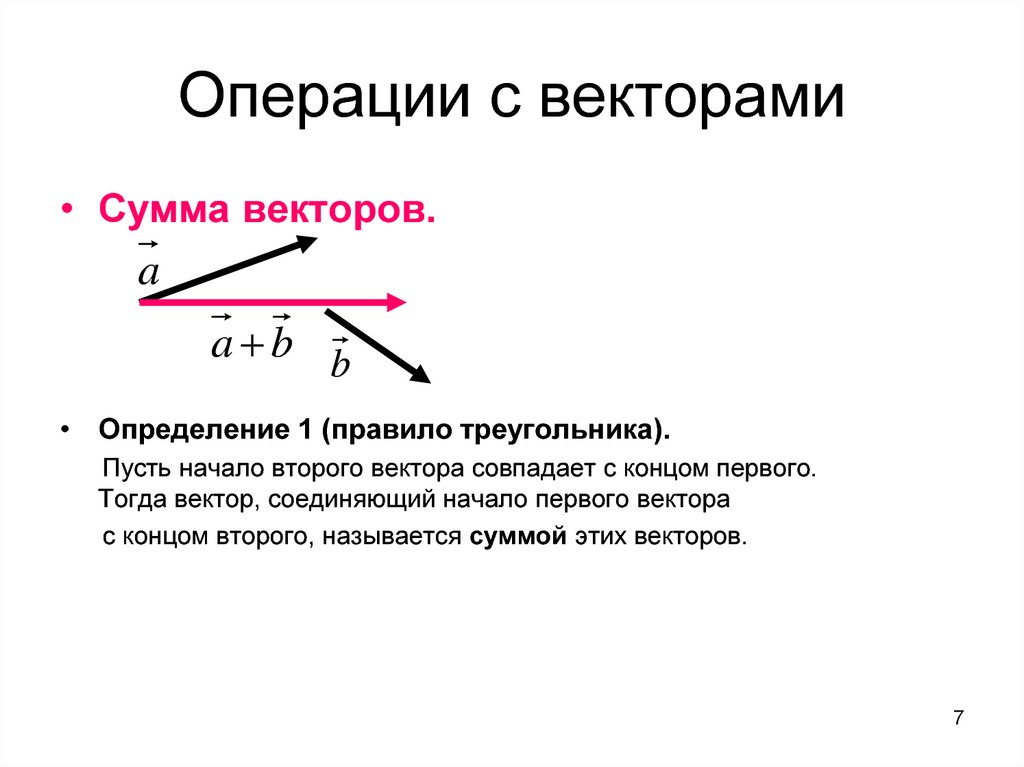
7. Операции с векторами

• Сумма векторов.
a
a b b
• Определение 1 (правило треугольника).
Пусть начало второго вектора совпадает с концом первого.
Тогда вектор, соединяющий начало первого вектора
с концом второго, называется суммой этих векторов.
7

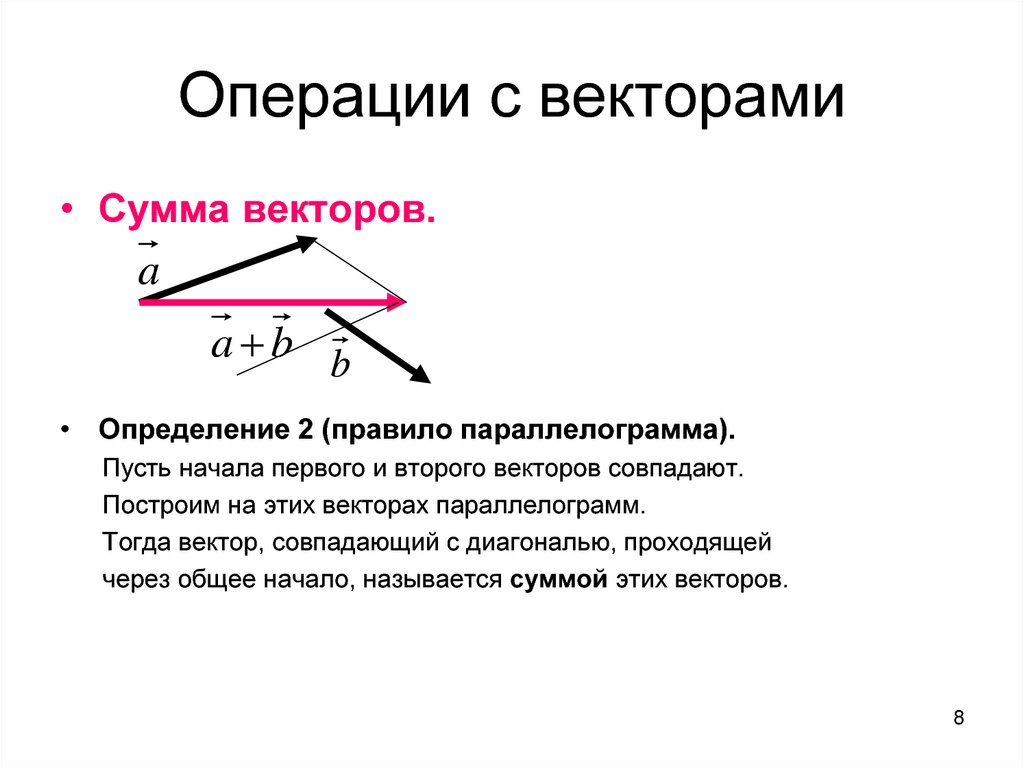
8. Операции с векторами

• Сумма векторов.
a
a b b
• Определение 2 (правило параллелограмма).
Пусть начала первого и второго векторов совпадают.
Построим на этих векторах параллелограмм.
Тогда вектор, совпадающий с диагональю, проходящей
через общее начало, называется суммой этих векторов.
8

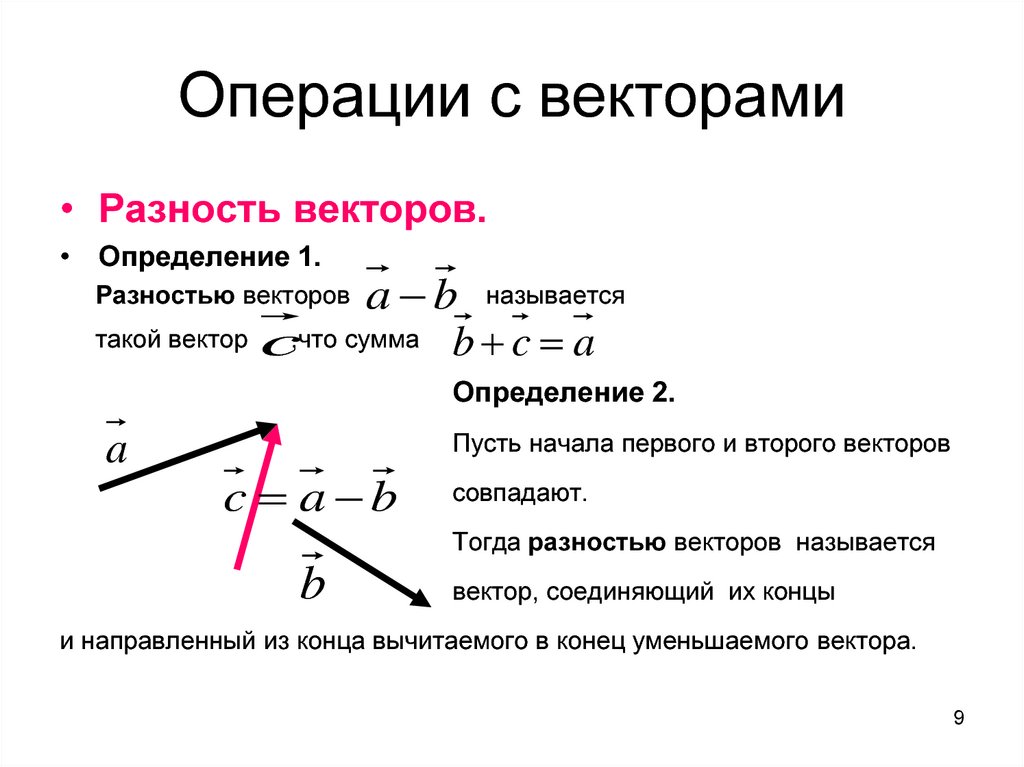
9. Операции с векторами

• Разность векторов.
• Определение 1.
a b называется
такой вектор c,что сумма b c a
Разностью векторов
Определение 2.
a
Пусть начала первого и второго векторов
c a b
совпадают.
Тогда разностью векторов называется
b
вектор, соединяющий их концы
и направленный из конца вычитаемого в конец уменьшаемого вектора.
9

10. Операции с векторами

• Произведение вектора на число.
• Определение.
Произведением вектора
вектор
a a,
коллинеарный вектору
равный по модулю
направленный при
a
на число
называется
a,
a
0
,
в ту же сторону, что и
0.
a,
и в противоположную сторону, если
10

11. Операции с векторами

• Пример.
Задан вектор
Построение :
a . Построить векторы
2a
a
a
1
1
2a, a, a .
2
2
1
a
2
a
1
a
2
• Теорема.
Пусть
a 0.
Векторы
b иa
коллинеарны тогда и только тогда,
когда найдется такая постоянная
, что b a
b a b a
11

12. Разложение векторов

• Разложение векторов по ортам.
• Определение 1.
Ортом вектора
a
называется вектор
a
o
,
имеющий единичную длину и то же направление,
что и вектор
a.
a
a
o
12

13. Разложение векторов

• Рассмотрим прямоугольную систему координат.
z
i , j, k
Векторы
-единичные (орты),
направленные по осям x, y, z (соответственно)
k
i
0
Определение 2.
j
y
x
(i, j , k )
Тройка векторов
называется
ортонормированным базисом
в пространстве.
• Теорема 3.
В пространстве любой вектор
d
можно разложить по
(i, j , k ) : d xi y j z k
Такое разложение единственное.
ортонормированному базису
13

14. Разложение векторов

• Определение 3.
Коэффициенты x, y, z разложения
d xi y j z k
называются прямоугольными координатами
вектора
d
:
d x, y, z
• Частный случай.
Если вектор
d
расположен на координатной плоскости хоy,
то разложение будет иметь вид
d xi y j
Коэффициенты х, у называются прямоугольными координатами
вектора на плоскости :
d x, y
14

15. Проекции вектора

• Рассмотрим вектор
M1M 2 и ось
M2
M1
0
x1
x2
• Определение.
Проекцией вектора M 1M 2 на ось
называется
разность проекций конца M 2 и началаM 1
вектора на эту ось;
Пр M1M 2 x2 x1
15

16. Проекции вектора

• В пространстве:
d x, y, z Прх d , Пру d , Прz d
• Следствие.
Если вектор
M1M 2 задан двумя точками,
M1 ( x1 , y1 , z1 ) - начало, M 2 ( x2 , y2 , z2 ) - конец,
то
M1M 2 x2 x1 , y2 y1 , z2 z1
16

17. Действия с векторами в координатной форме

• Сумма и разность векторов,
произведение вектора на число.
Пусть
Тогда
a x1 , y1 , z1 и b x2 , y2 , z 2
1.
2.
a b x1 x2 , y1 y2 , z1 z2
a x1 , y1 , z1
Модуль вектора
a x y z
2
1
Орт вектора
2
1
x y z
a 1 , 1, 1
a a a
2
1
o
17

18. Действия с векторами в координатной форме

Необходимое и достаточное условие коллинеарности
векторов, заданных в координатной форме.
Два ненулевых вектора коллинеарны тогда и только тогда, когда
соответствующие координаты пропорциональны.
Пусть
Тогда
a x1 , y1 , z1 и b x2 , y2 , z 2
x1
y1
z1
a b
x2
y2
z2
Доказательство.
x1
y1
z1
x1 x2
a b a b y1 y2
x
y
z
z
z
2
2
2
2
1
18

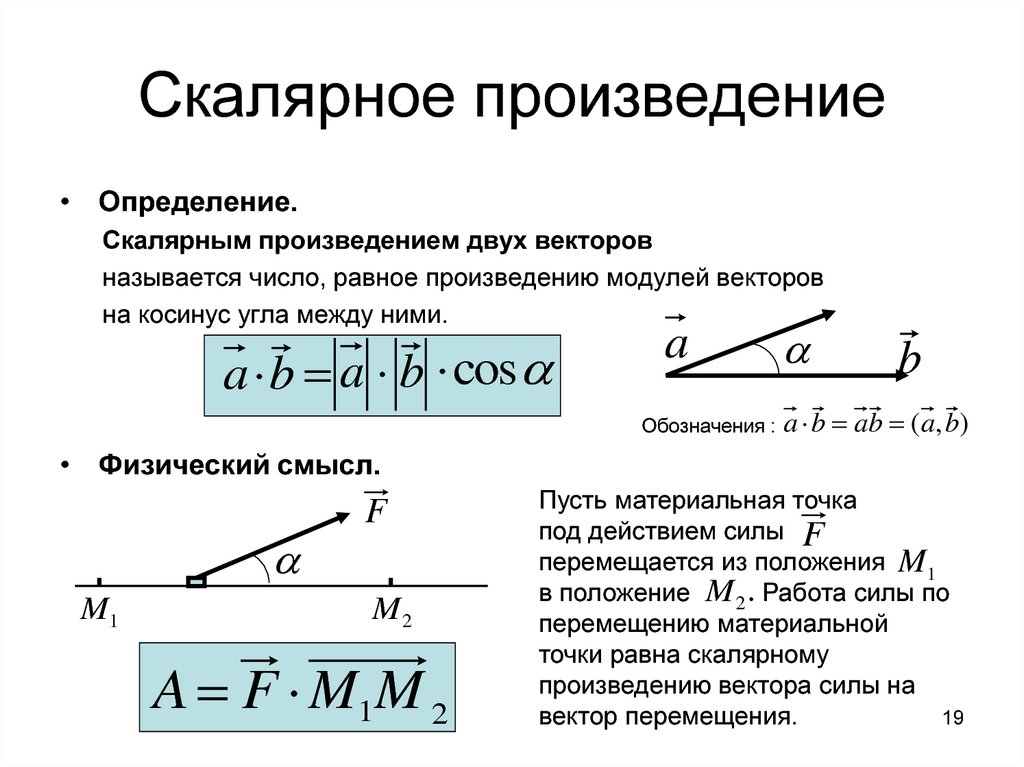
19. Скалярное произведение

• Определение.
Скалярным произведением двух векторов
называется число, равное произведению модулей векторов
на косинус угла между ними.
a b a b cos
a
Обозначения :
b
a b ab ( a, b)
• Физический смысл.
M1
F
M2
A F M 1M 2
Пусть материальная точка
под действием силы F
перемещается из положения M 1
в положение M 2 . Работа силы по
перемещению материальной
точки равна скалярному
произведению вектора силы на
вектор перемещения.
19

20. Скалярное произведение

• Свойства скалярного произведения.
2.
a b b a
( a ) b ( a b )
3.
a (b c) a b a c
1.
4.
a b a Прa b b Прb a
• Следствия из формулы 4 :
Прb a
a b
b
Прa b
a b
a
20

21. Скалярное произведение

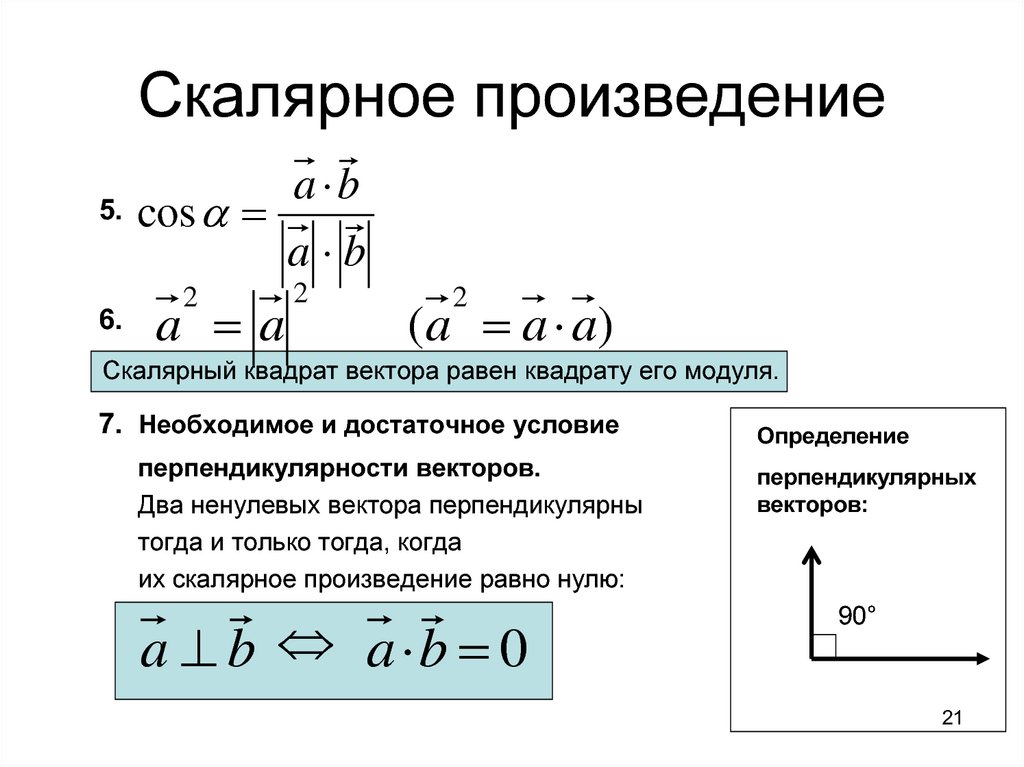
5.
6.
cos
2
a a
a b
a b
2
2
(a a a)
Скалярный квадрат вектора равен квадрату его модуля.
7. Необходимое и достаточное условие
перпендикулярности векторов.
Два ненулевых вектора перпендикулярны
тогда и только тогда, когда
их скалярное произведение равно нулю:
a b a b 0
Определение
перпендикулярных
векторов:
90°
21

22. Скалярное произведение

• Скалярное произведение векторов,
заданных в координатной форме.
Пусть
Тогда
a x1 , y1 , z1 и b x2 , y2 , z 2
a b x1 x2 y1 y2 z1 z2
Скалярное произведение векторов равно
сумме произведений соответствующих координат.
Условие перпендикулярности векторов
в координатной форме :
a b x1 x2 y1 y2 z1 z 2 0
22

23. Векторное произведение

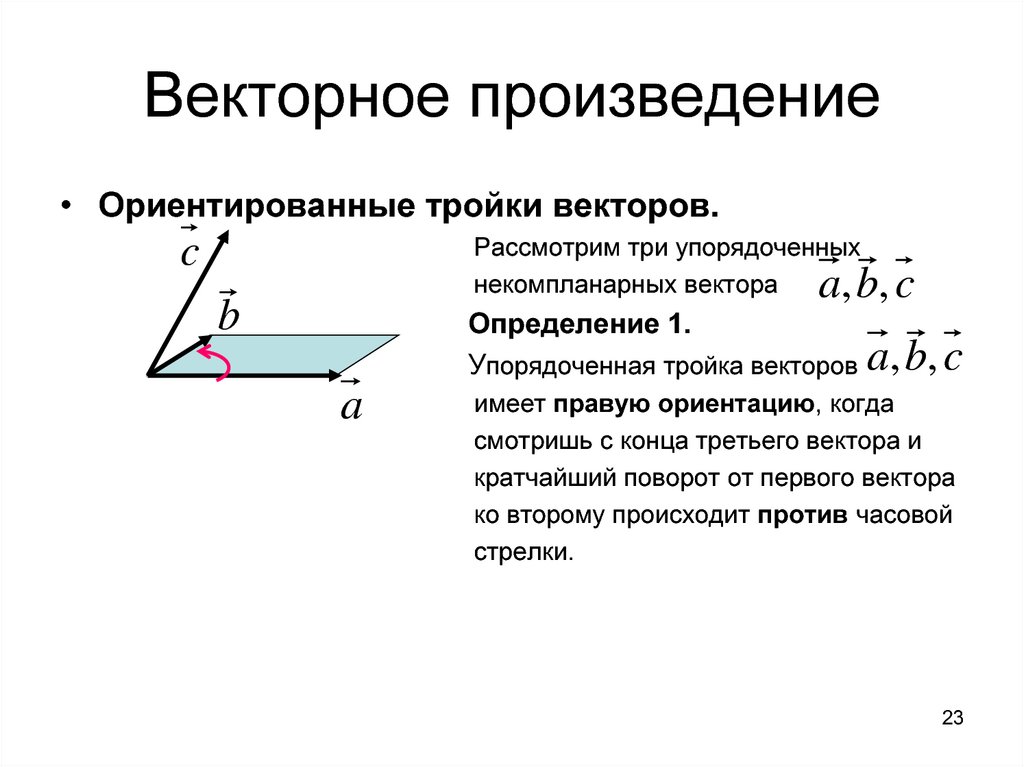
• Ориентированные тройки векторов.
Рассмотрим три упорядоченных
некомпланарных вектора
c
a , b, c
b
Определение 1.
Упорядоченная тройка векторов
a
a , b, c
имеет правую ориентацию, когда
смотришь с конца третьего вектора и
кратчайший поворот от первого вектора
ко второму происходит против часовой
стрелки.
23

24. Векторное произведение

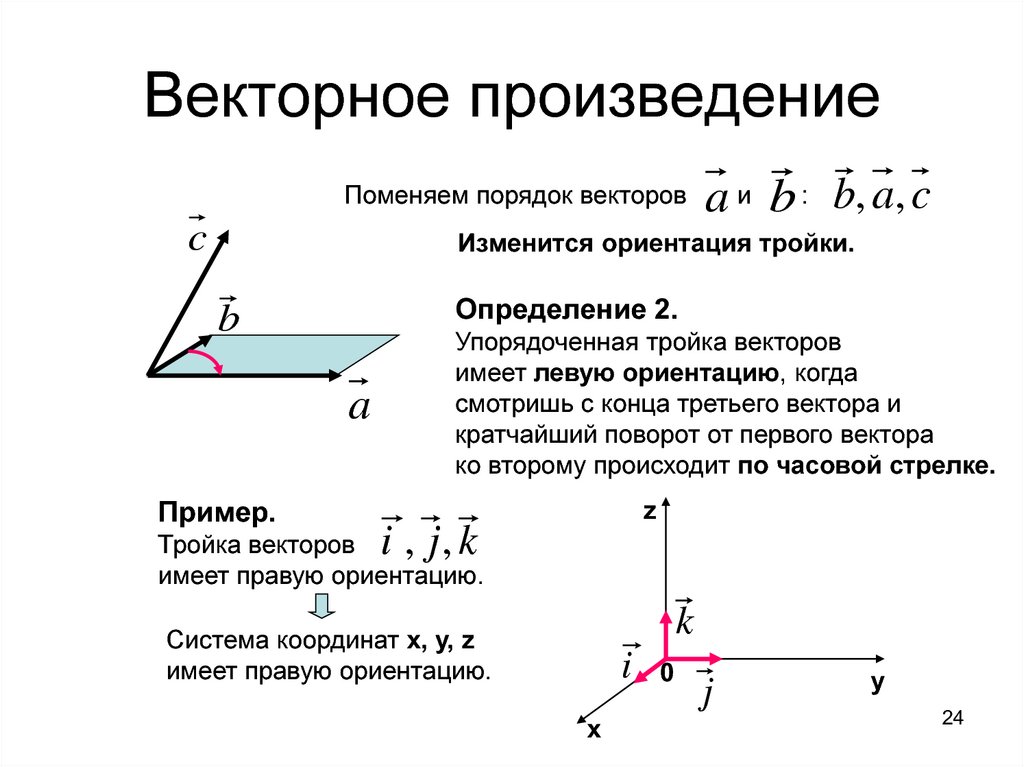
Поменяем порядок векторов
c
a и b : b, a , c
Изменится ориентация тройки.
Определение 2.
b
a
Пример.
Упорядоченная тройка векторов
имеет левую ориентацию, когда
смотришь с конца третьего вектора и
кратчайший поворот от первого вектора
ко второму происходит по часовой стрелке.
z
i , j, k
Тройка векторов
имеет правую ориентацию.
k
Система координат х, у, z
имеет правую ориентацию.
i
x
0
j
y
24

25. Векторное произведение

• Определение 3.
Векторным произведением двух векторов a и
называется третий вектор a b ,
a b
удовлетворяющий трем условиям :
1.
a b a b sin
2.
a b a и a b b
3. Тройка векторов
a, b, a b
b
b
a
имеет правую ориентацию.
Обозначения :
a b [ a, b]
25

26. Векторное произведение

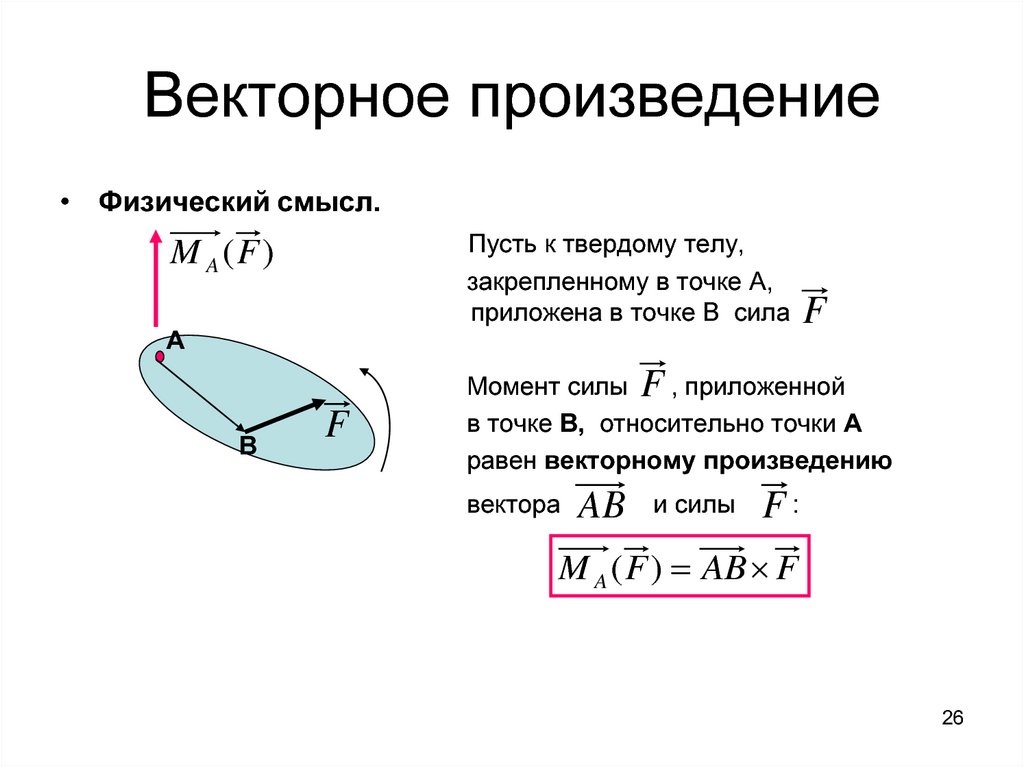
• Физический смысл.
Пусть к твердому телу,
закрепленному в точке А,
приложена в точке В сила
M A (F )
А
В
F
F
Момент силы F , приложенной
в точке В, относительно точки А
равен векторному произведению
вектора
AB
и силы
F:
M A ( F ) AB F
26

27. Векторное произведение

• Свойства векторного произведения.
1. a b b a
2. ( a ) b (a b)
3. a (b c) a b a c
4. Геометрический смысл .
Модуль векторного произведения двух векторов
численно равен площади параллелограмма,
построенного на этих векторах:
a b S
b
a
27

28. Векторное произведение

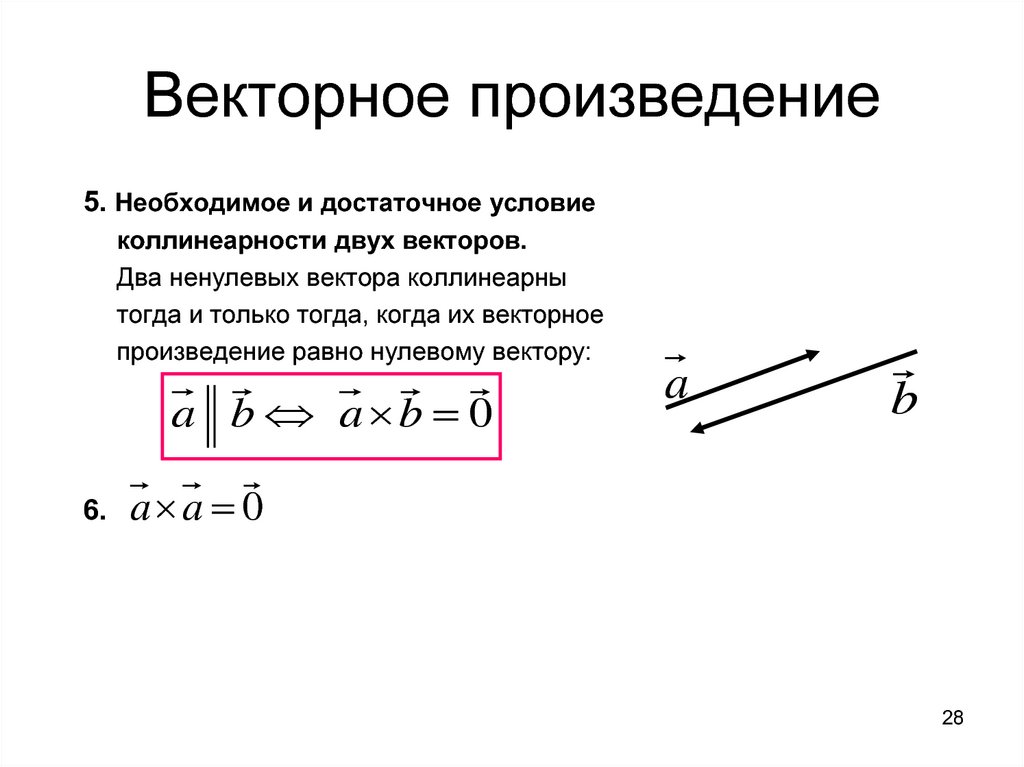
5. Необходимое и достаточное условие
коллинеарности двух векторов.
Два ненулевых вектора коллинеарны
тогда и только тогда, когда их векторное
произведение равно нулевому вектору:
a b a b 0
6.
a
b
a a 0
28

29. Векторное произведение

• Векторное произведение векторов,
заданных в координатной форме.
Пусть
Тогда
a x1 , y1 , z1 и b x2 , y2 , z 2
i j k
a b x1 y1 z1
x2 y2 z2
y1 z1
x1 z1
x1 y1
a b y z i x z j x y k
2 2
2 2
2 2
29

30. Смешанное произведение

• Определение.
Смешанным произведением трех векторов
называется векторное произведение первых двух
векторов, умноженное скалярно на третий вектор:
abc ( a b) c
a b c ( a , b, c )
Обозначения:
Замечание.
Результат смешанного произведения трех векторов
является скалярной величиной.
30

31. Смешанное произведение

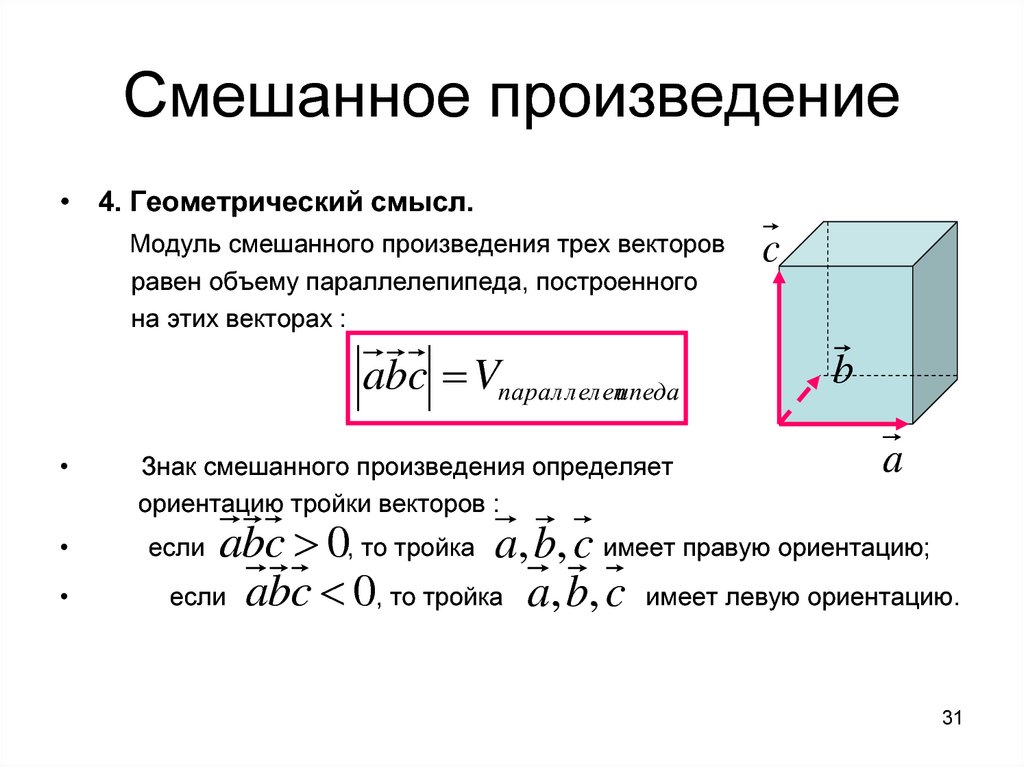
• 4. Геометрический смысл.
Модуль смешанного произведения трех векторов
равен объему параллелепипеда, построенного
на этих векторах :
abc Vпараллелепипеда
Знак смешанного произведения определяет
ориентацию тройки векторов :
c
b
a
abc 0, то тройка a, b, c имеет правую ориентацию;
если abc 0, то тройка a , b, c имеет левую ориентацию.
если
31

32. Смешанное произведение

• 5. Необходимое и достаточное условие
компланарности трех векторов.
Три ненулевых вектора компланарны
тогда и только тогда, когда смешанное
произведение этих векторов равно нулю.
Смешанное произведение векторов,
заданных в координатной форме.
Пусть
a x1 , y1 , z1
b x2 , y2 , z 2
c x3 , y3 , z3
Тогда
x1 y1 z1
abc x2 y2 z2
x3 y3 z3
32