Элементы векторной алгебры

1. ЭЛЕМЕНТЫ ВЕКТОРНОЙ АЛГЕБРЫ

Скалярные и векторные величины
Линейные операции над векторами
Угол между векторами. Проекция
вектора на ось
Линейная комбинация векторов. Базис
Прямоугольная декартова система
координат
Линейные операции над векторами,
заданными в координатной форме

2. Скалярные и векторные величины

Определение скалярной величины
Определение векторной величины
Длина вектора
Нулевой вектор
Коллинеарность векторов. Компланарность
векторов
Равенство векторов
Противоположный вектор. Единичный вектор

3. Определение скалярной величины

Величина, определяемая
заданием своего
численного значения,
называется скалярной
величиной
Примерами скалярных
величин являются длина,
площадь, объем, масса,
температура и др.
Скалярные величины
обозначаются символами
a , b, , A, B
и изображаются точками
соответствующей числовой
оси

4. Определение векторной величины

Величина, определяемая заданием
своего численного значения и
направления, называется
векторной величиной.
Примерами векторных величин
являются сила, скорость,
ускорение и др.
Векторные величины
изображаются с помощью векторов
- направленных отрезков.

5.

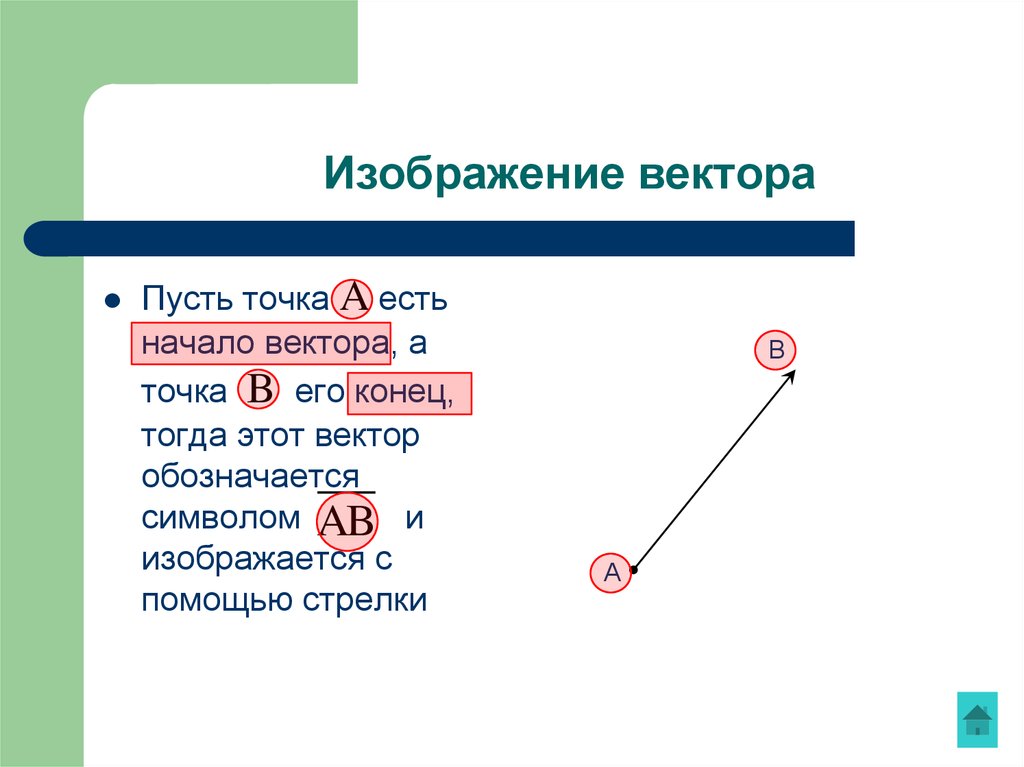
Изображение вектора
Пусть точка A есть
начало вектора, а
точка B его конец,
тогда этот вектор
обозначается
символом AB и
изображается с
помощью стрелки
B
A

6. Длина вектора

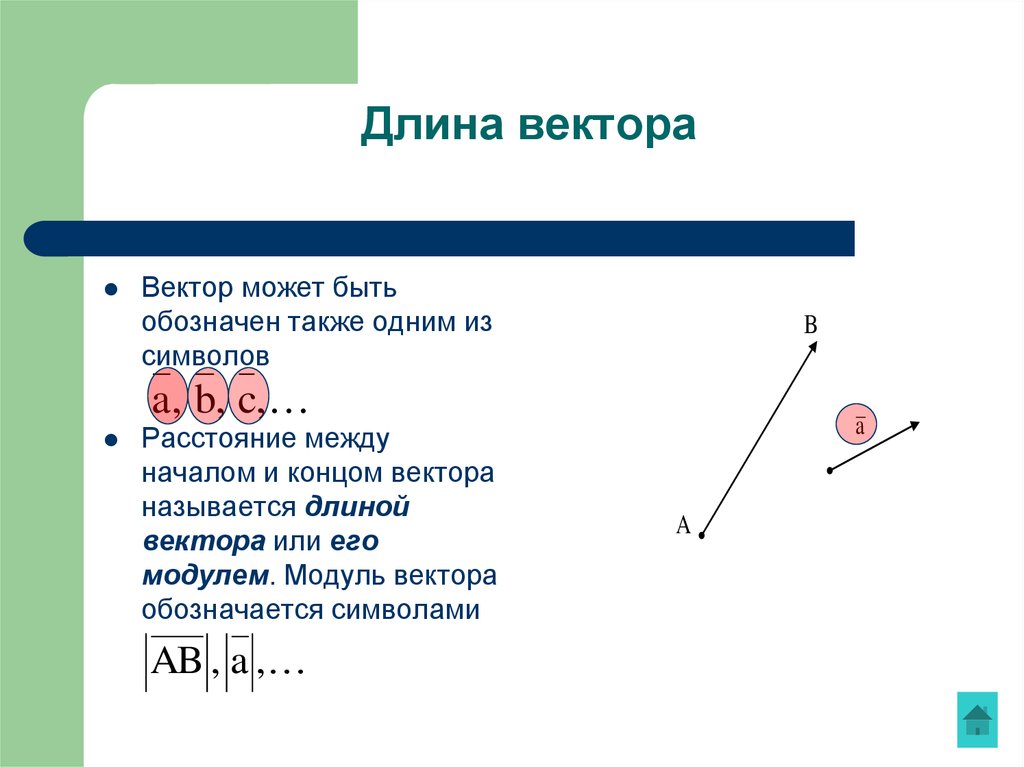
Вектор может быть
обозначен также одним из
символов
B
a, b, c,
Расстояние между
началом и концом вектора
называется длиной
вектора или его
модулем. Модуль вектора
обозначается символами
AB , a ,
a
A
Рис. 1.1

7. Нулевой вектор

Вектор, начало которого
совпадает с его концом,
называется нулевым вектором
и обозначается 0
Нулевой вектор не имеет
определенного направления и
его 0 0
O

8. Коллинеарность векторов Компланарность векторов

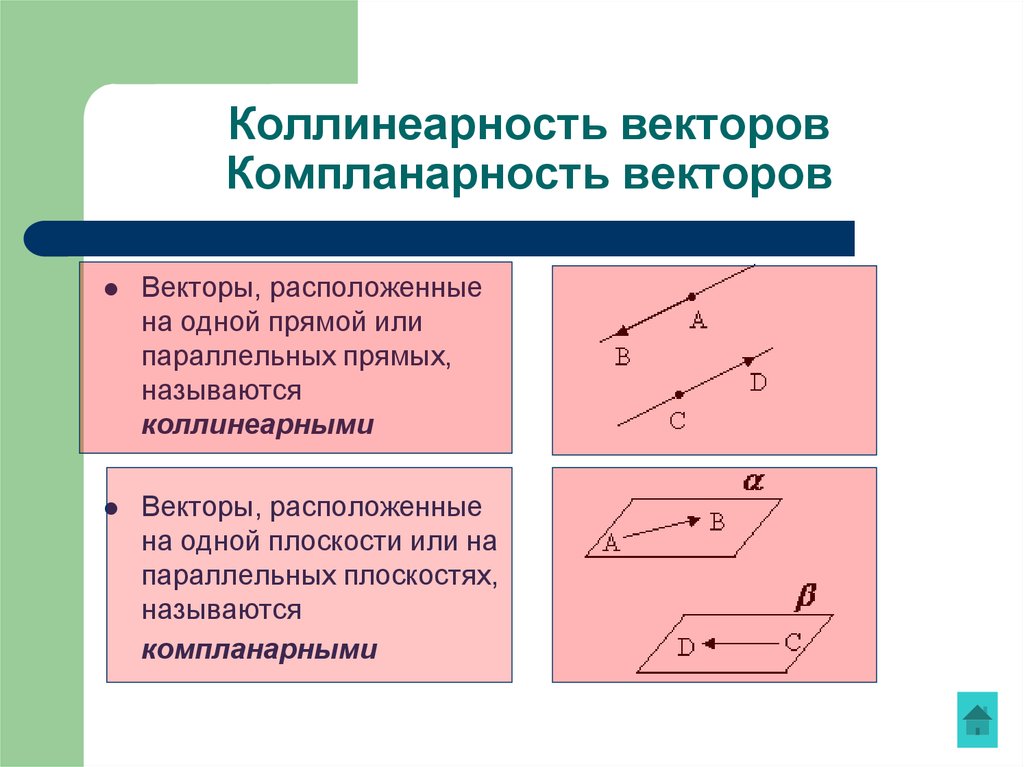
Векторы, расположенные
на одной прямой или
параллельных прямых,
называются
коллинеарными
Векторы, расположенные
на одной плоскости или на
параллельных плоскостях,
называются
компланарными

9. Равенство векторов

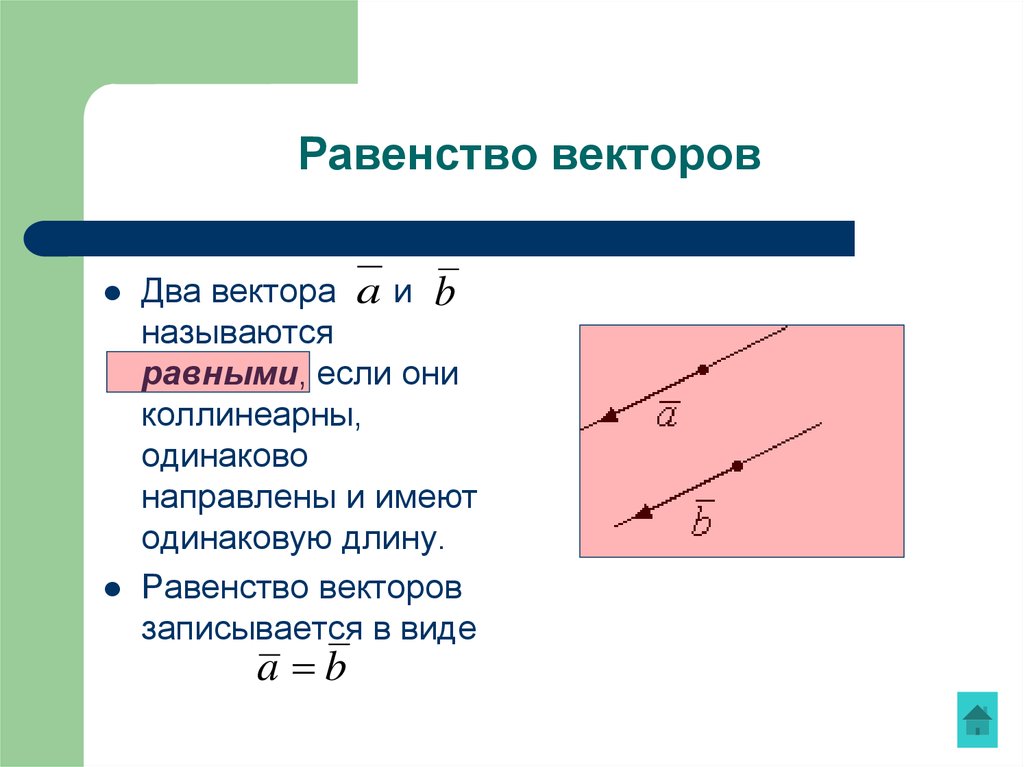
Два вектора a и b
называются
равными, если они
коллинеарны,
одинаково
направлены и имеют
одинаковую длину.
Равенство векторов
записывается в виде
a b

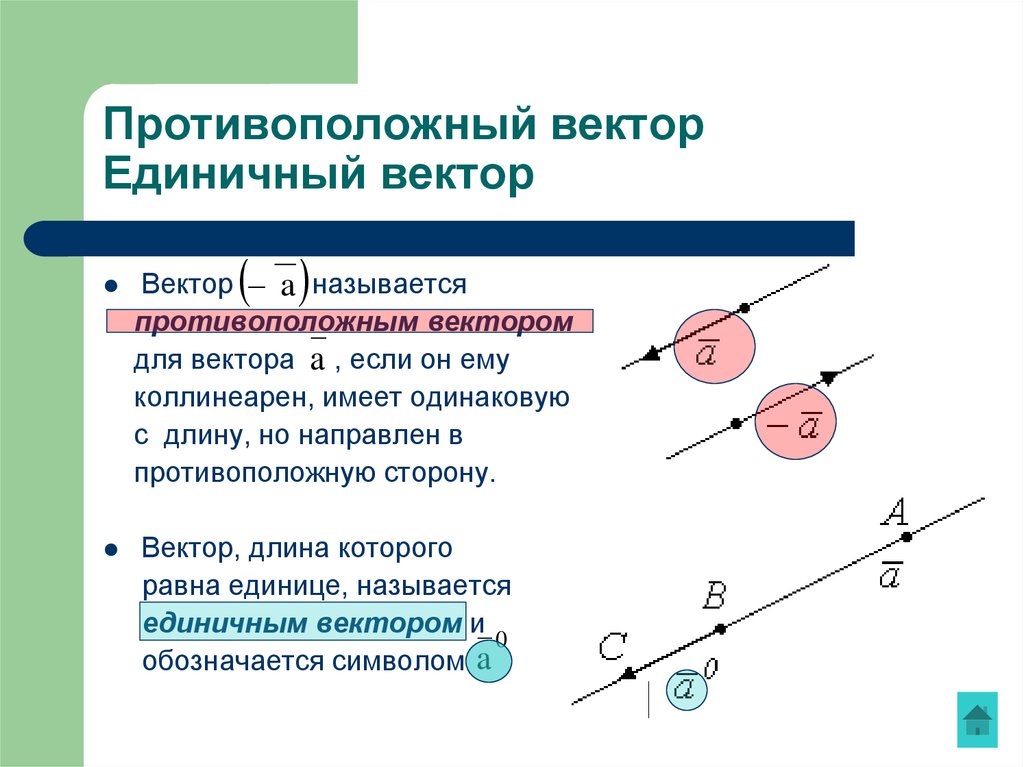
10. Противоположный вектор Единичный вектор

Вектор a называется
противоположным вектором
для вектора a , если он ему
коллинеарен, имеет одинаковую
с длину, но направлен в
противоположную сторону.
Вектор, длина которого
равна единице, называется
единичным вектором и
0
обозначается символом a

11. Линейные операции над векторами

Сложение векторов
Переместительный закон сложения векторов
Сочетательный закон сложения векторов
Разность векторов
Умножение вектора на число
Распределительный и сочетательный законы
умножения вектора на число

12. Сложение векторов

Суммой векторов a и b
называется третий вектор
c a b , начало которого
совпадает с началом
вектора a , а конец – с
концом вектора b , при
условии, что начало
вектора b приложено к
концу вектора a
c a b
b
a

13. Переместительный закон сложения векторов

Сумма векторов
может быть найдена и
по правилу
параллелограмма
a
N
Q
b
Сложение векторов
подчиняется
переместительному
закону a b b a
M
b
a
P

14. Сочетательный закон сложения векторов

Сложение векторов
подчиняется
сочетательному
закону
a b c a b c

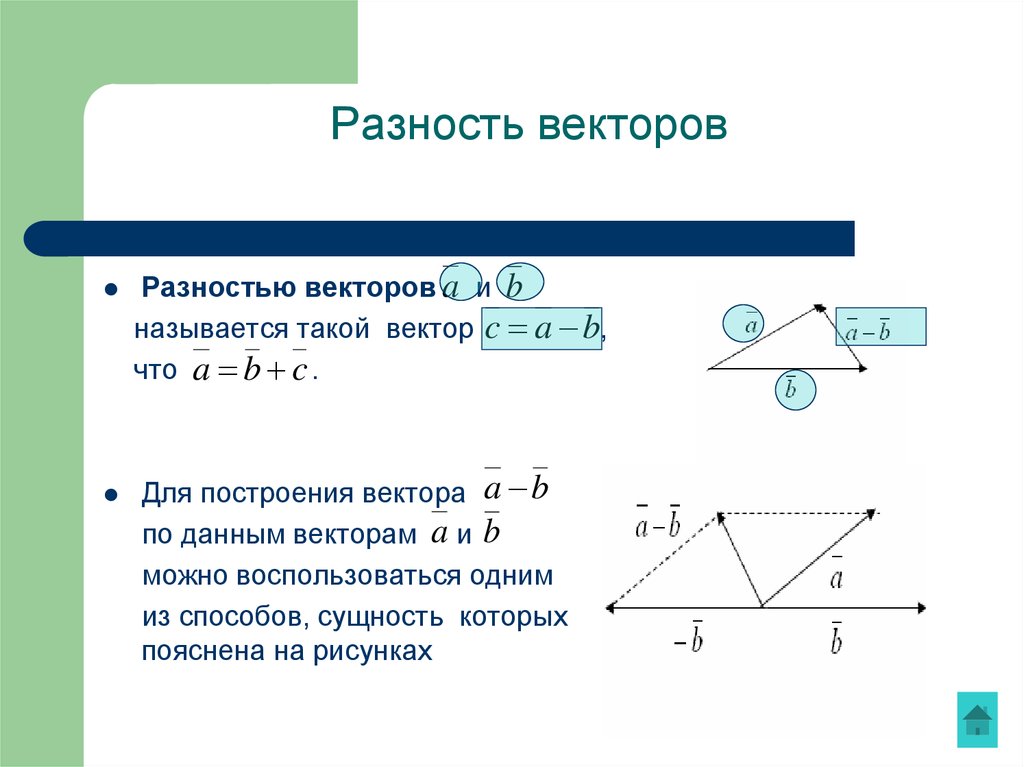
15. Разность векторов

Разностью векторов a и b
называется такой вектор c a b,
что a b c .
Для построения вектора a b
по данным векторам a и b
можно воспользоваться одним
из способов, сущность которых
пояснена на рисунках

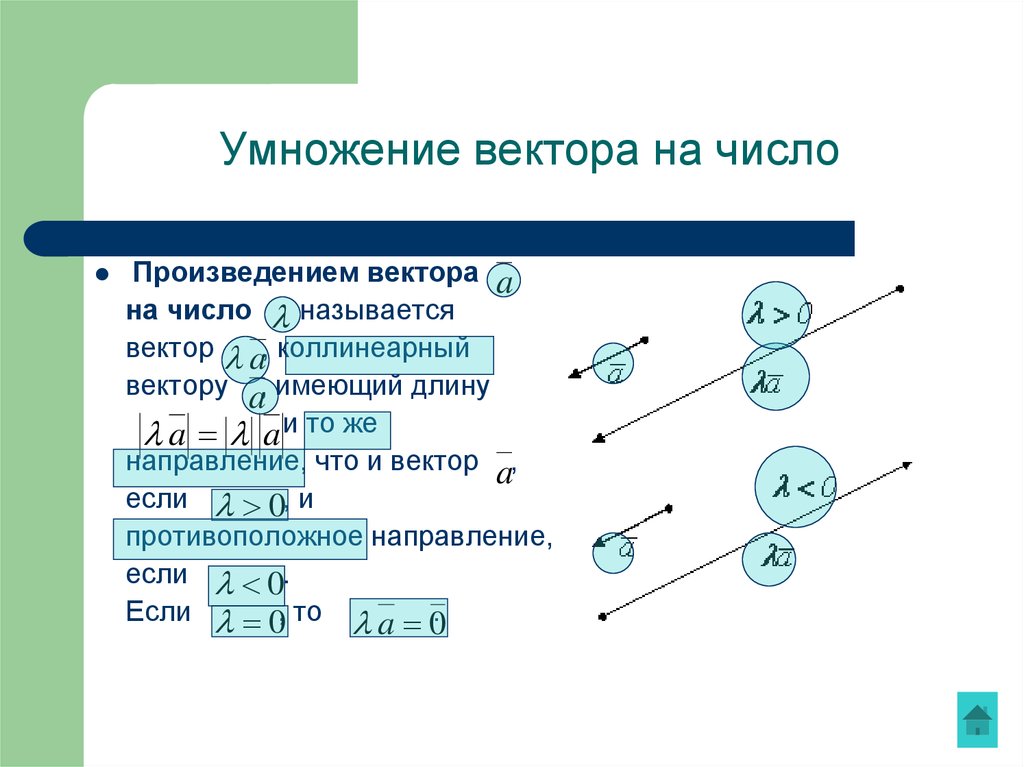
16. Умножение вектора на число

Произведением вектора a
на число называется
вектор a, коллинеарный
вектору a, имеющий длину
a a и то же
направление, что и вектор a,
если 0, и
противоположное направление,
если 0.
Если 0, то a 0.

17. Следствие 1 о коллинеарности векторов

Из определения
умножения вектора на
число следует, что
если b a , то
векторы a и b
коллинеарны.
Очевидно, что если a
и b коллинеарные
векторы, то b a .

18. Следствие 2. Следствие 3.

Следствие 2.
Противоположный вектор a
можно рассматривать как
произведение вектора a на
то есть a 1 a
a 1 a
a aa
0
1 ,
Следствие 3. Пусть дан вектор a.
0
Рассмотрим вектор a , коллинеарный a ,
направленный, как a , имеющий длину,
равную единице. Тогда, согласно
операции умножения вектора на число,
следует, что

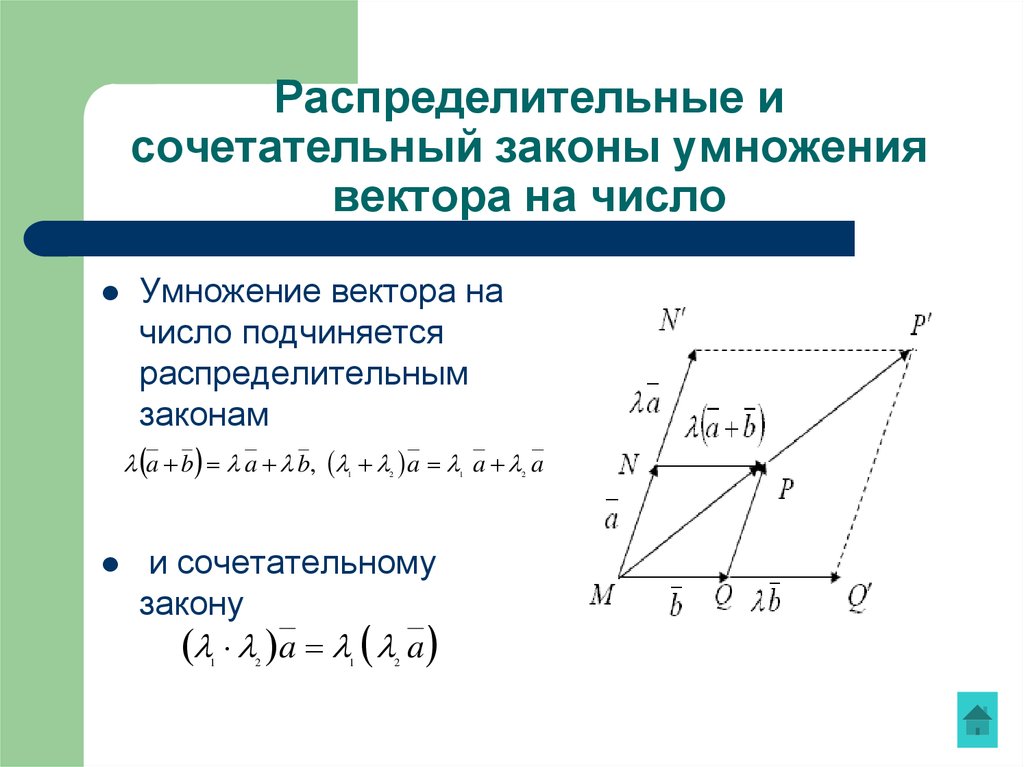
19. Распределительные и сочетательный законы умножения вектора на число

Умножение вектора на
число подчиняется
распределительным
законам
a b a b, a a a
1
2
1
и сочетательному
закону
a a
1
2
1
2
2
Рис. 1.7

20. Угол между векторами. Проекция вектора на ось.

Угол между векторами
Определение проекции вектора на ось
Проекция суммы векторов на ось

21. Угол между векторами

Углом между
векторами a и b
называется
наименьший угол
0
на который нужно
повернуть один из
заданных векторов до
его совпадения со
вторым

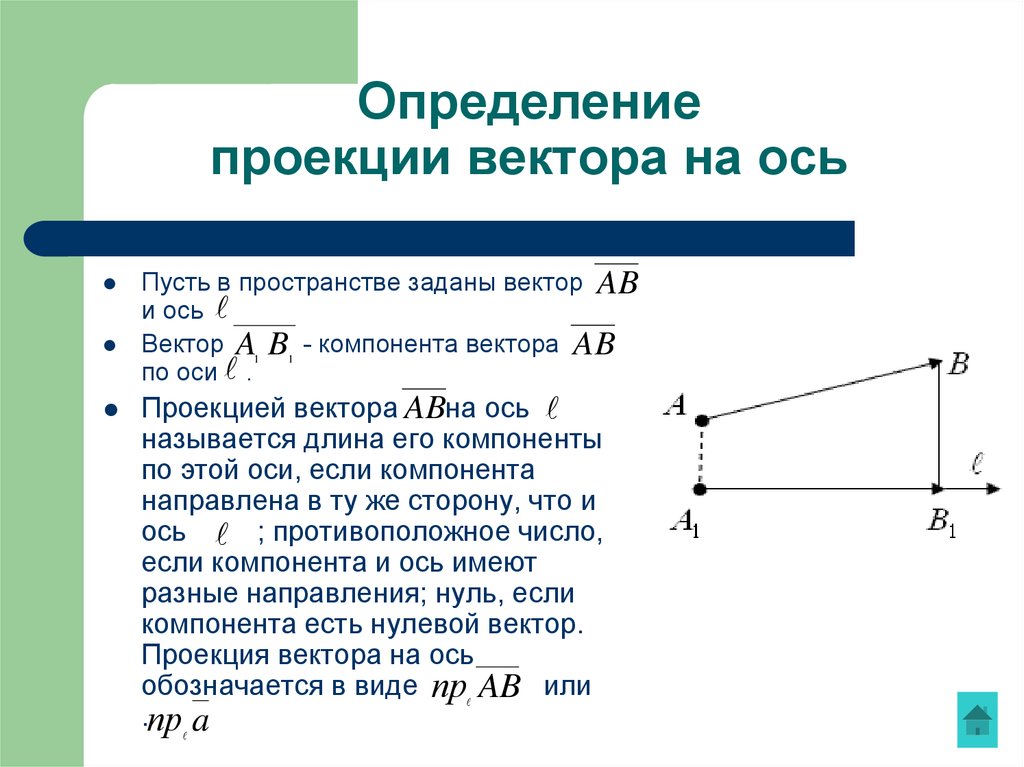
22. Определение проекции вектора на ось

Пусть в пространстве заданы вектор AB
и ось
Вектор A1 B1 - компонента вектора AB
по оси .
Проекцией вектора ABна ось
называется длина его компоненты
по этой оси, если компонента
направлена в ту же сторону, что и
ось ; противоположное число,
если компонента и ось имеют
разные направления; нуль, если
компонента есть нулевой вектор.
Проекция вектора на ось
обозначается в виде пр AB или
.пр a

23. Теорема Проекция вектора на ось

Теорема Проекция
вектора a на ось
равна модулю
вектора ,
умноженному на a
косинус угла
между вектором
и осью:
пр a a cos
Рис. 1.11
Рис. 1.11

24. Проекция суммы векторов на ось

Теорема. Проекция суммы векторов на
ось равна сумме проекции слагаемых
векторов на ту же ось:
пр a a a пр a пр a пр a
1
2
k
1
2
k
a
Теорема.
умножить на
Если вектор
число , то его проекция на
ось
пр a пр a
умножится на это число:

25. Линейная комбинация векторов. Базис

Линейная комбинация векторов
Линейная зависимость и независимость
векторов
Определение базиса пространства
Базис пространства
Разложение вектора по базисным вектрам

26. Линейная комбинация векторов

ОПРЕДЕЛЕНИЕ Пусть заданы векторы
a , a , , a и числа , , , . Выражение
a a a
называется линейной
комбинацией векторов a , a , , a
1
1
2
1
k
2
2
1
k
2
k
k
1
2
k

27. Линейная зависимость и независимость векторов

ОПРЕДЕЛЕНИЕ Если равенство
a a a 0
возможно только при всех , , , ,
1
1
2
2
k
k
1
2
k
равных нулю, то векторы a , a , , a
называются линейно-независимыми.
Если же это равенство справедливо не
при всех 0 , где i 1,2, , k , то векторы
называются линейно-зависимыми.
1
i
2
k

28. Определение базиса пространства

ОПРЕДЕЛЕНИЕ Любая группа,
составленная из максимального числа
линейно-независимых векторов
некоторого пространства R , называется
базисом этого пространства.
Число векторов базиса называется
размерностью пространства.
n

29.

Базис пространства
Базисом на прямой
(пространство R 1 ) является
любой ненулевой вектор этой
прямой. Размерность прямой
равна единице.
Базисом на плоскости
(пространство R 2) являются
любые два неколлинеарных
вектора этой плоскости.
Размерность плоскости равна
двум.
Базисом в объемном
3
пространстве (пространство R )
являются любые три
некомпланарные вектора.
Размерность этого пространства
равна трем.

30. Разложение вектора по базисным векторам

Представление вектора a в форме
a a a a
1
1
2
2
n
n
называется разложением этого вектора по
базисным векторам.
Числа , , , разложения называются
координатами вектора a по базису a , a , ., a
Этот факт записывается в виде a ; . ;
Векторы a , a , , a называется
компонентами вектора a по базисным векторам
1
2
n
1
1
1
a , a , a .
1
2
n
1
2
2
n
n
2
2
n
n

31. Прямоугольная декартова система координат

Определение прямоугольной декартовой
системы координат
Координаты вектора. Длина вектора.
Направляющие косинусы вектора

32. Определение прямоугольной декартовой системы координат

ОПРЕДЕЛЕНИЕ Пусть в пространстве R
векторы a , a , a
образуют базис
3
этого пространства. Выберем в R
произвольную точку O и отложим с
началом в этой точке базисные векторы.
Совокупность точки O и трех базисных
векторов называется системой
координат в пространстве R.3
Совокупность точки O и базисных
векторов i, j , k называется
прямоугольной декартовой системой
3
координат в пространстве R .
3
1
2
3

33. Координаты вектора. Длина вектора.

Координаты точки M R3
записываются в форме M ( x; y; z )
Пусть вектор a OM
задан в координатной
форме a x; y; z .
Так как этот вектор
совпадает с диагональю
прямоугольного
параллелепипеда, то его
длина равна длине этой
диагонали.
Следовательно,
a OM x y z
2
2
2

34. Направляющие косинусы вектора

ОПРЕДЕЛЕНИЕ Косинусы углов
cos
x
,
x y z
2
2
2
cos
, ,
cos
y
,
x y z
2
z
x y z
2
, определяемые
2
2
2
2
называются направляющими косинусами вектора .a
Нетрудно проверить, что направляющие косинусы связаны
между собой соотношением
cos cos cos 1
2
2
2

35. Линейные операции над векторами, заданными в координатной форме

Действия на векторами, заданными в
координатной форме
Условие коллинеарности двух векторов
Задача определения расстояния между
двумя точками
Деление отрезка в данном отношении

36. Действия над векторами, заданными в координатной форме

Пусть векторы a и a заданы в координатной форме:
1
2
a x ; y ; z x i y j z k ,
1
1
1
1
1
1
1
a x ; y ; z x i y j z k .
2
2
2
2
2
2
2
Непосредственно из теорем о проекциях векторов на
ось и определения координат вектора вытекают
правила:
x x, y y, z z;
a a
a a x x i y y j z z k ;
a a x x i y y j z z k ;
a x i y j z k , где R
1
2
1
2
1
2
1
2
1
2
1
1
1
1
2
1
1
2
2
1
1
2
2
1
1
1
2
2

37. Условие коллинеарности двух векторов

ПРИМЕР
Установить условие коллинеарности
векторов a1 x1; y1; z1 , a 2 x 2 ; y 2 ; z 2
Решение. Так как векторы коллинеарны,
то a1 a 2 , где некоторое число. Имеем
x1 i y1 j z1 k x 2 i y 2 j z 2 k
x1 y1 z1
x x 2 , y1 y 2 , z1 z 2
x 2 y2 z2

38. Задача определения расстояния между двумя точками

Пусть в пространстве R
заданы своими
координатами две точки
M x ; y ; z и M x ; y ; z .
Так как длина вектора M1M 2
равна расстоянию между
точками M1 и M 2 , то
3
1
1
1
1
d MM
1
2
2
2
2
2
x x y y z z
2
2
1
2
2
1
2
2
1
.

39.

Задача деления отрезка в данном отношении
Пусть даны две точки M1 x 1 ; y1 ; z1 и M 2 x 2 ; y 2 ; z 2 . Требуется
на прямой M1M 2
найти точку M 0 x 0 ; y 0 ; z 0 , которая разделила бы отрезок M1M 2
в заданном отношении , т.е. так, что M1M 0 M 0 M 2 .
Находим длины векторов:
M1M 0 x 0 x 1 ; y 0 y1 ; z 0 z1 ,
M 0 M 2 x 2 x 0 ; y 2 y 0 ; z 2 z 0 .
M1M 0 M 0 M 2
Равенство
примет
x 0 x 1 x 2 x 0 , y 0 y1 y 2 y 0 , z 0 z1 z 2 z 0 .
Определяя x 0 , y 0 , z 0 из этих равенств, получим
x x2
y y2
z z2
x0 1
, y0 1
, z0 1
,
1
1
1
где R, 1 .
В частности, при
x0
вид
1 получим формулы деления отрезка пополам:
x1 x 2
y y2
z + z2
, y0 1
, z0 1
2
2
2
.