Элементы векторной алгебры и аналитической геометрии

1. Лекция №2

1
Лекция №2
Элементы векторной алгебры и
аналитической геометрии:
Векторы. Линейные операции над векторами. Базис
на плоскости и в пространстве. Координаты вектора.
Скалярное произведение. Векторное произведение.
Смешанное произведение векторов. Аналитическая
геометрия на плоскости.

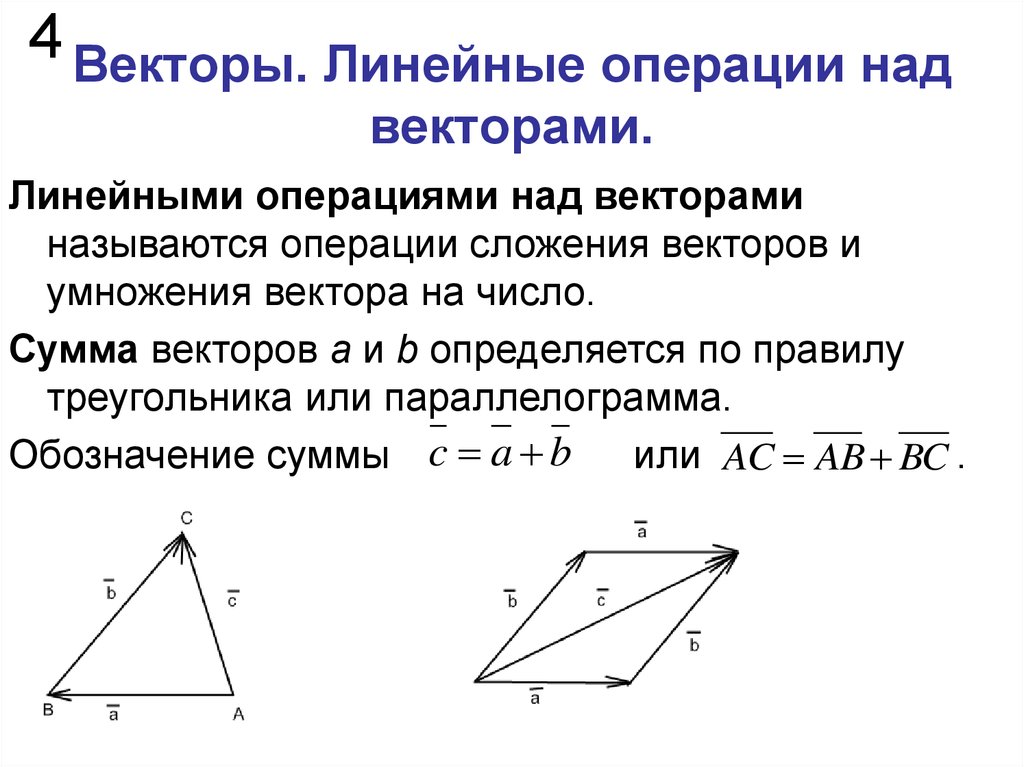
2. Векторы. Линейные операции над векторами.

2 Векторы. Линейные операции над
векторами.
Вектор – направленный отрезок.
Обозначение a AB .
Длина вектора – длина отрезка АВ.
Обозначение длины
a AB
или a a .
Коллинеарные векторы – векторы, параллельные одной
прямой.
Обозначения:
a b – векторы сонаправлены;
a b – векторы противоположно направлены;
– в общем случае (без указания взаимной
a || b
направленности).

3. Векторы. Линейные операции над векторами.

3 Векторы. Линейные операции над
векторами.
Равные векторы – векторы, удовлетворяющие
условиям :
1) имеют одинаковую длину;
2) коллинеарны;
3) сонаправлены.
Компланарные векторы — векторы, параллельные
одной плоскости.

4. Векторы. Линейные операции над векторами.

4 Векторы. Линейные операции над
векторами.
Линейными операциями над векторами
называются операции сложения векторов и
умножения вектора на число.
Сумма векторов a и b определяется по правилу
треугольника или параллелограмма.
Обозначение суммы c a b
или AC AB BC .

5. Векторы. Линейные операции над векторами.

5 Векторы. Линейные операции над
векторами.
Произведением вектора ā на число λ называется
вектор b , удовлетворяющий следующим
условиям:
1) b a ;
b aпри λ<0 .
2) b a при λ>0 и
Обозначение b a .

6. Базис на плоскости и в пространстве. Координаты вектора

6 Базис на плоскости и в пространстве.
Координаты вектора
Два неколлинеарных вектора a и b образуют
базис на плоскости.
Три некомпланарных вектора a , b и c
образуют базис в пространстве.
Ортонормированный (декартовый) базис –
это базис составляющие векторы которого
взаимно перпендикулярны и имеют
единичную длину.
Будем обозначать декартовый базис на
плоскости -i ,j ; в пространстве -i ,j k,

7. Базис на плоскости и в пространстве. Координаты вектора

7 Базис на плоскости и в пространстве.
Координаты вектора
Разложить вектор по базису – значит представить его
в виде линейной комбинации базисных
векторов, т.е. в форме
d a b
- на плоскости,
d a b c
- в протранстве.
Числа α, β, γ, (коэффициенты линейной
комбинации)
называются
координатами
вектора в данном базисе. Вектор может быть
задан в координатной форме: d ; – на
плоскости; d ; ; – в пространстве.

8. Базис на плоскости и в пространстве. Координаты вектора

8 Базис на плоскости и в пространстве.
Координаты вектора
Линейным операциям над векторами
a a1; a2 ; a3 и b b1 ; b2 ; b3
1.
2.
3.
a b a1 b1 ; a2 b2 ; a3 b3
a b a1 b1 ; a2 b2 ; a3 b3
a a1; a2 ; a3
Если заданы координаты начала и конца вектора
и
B y1; y2 ; y3
A x ;x ;x
1
2
3
тогда координаты вектора вычисляются:
a AB y1 x1; y2 x2 ; y3 x3

9. Базис на плоскости и в пространстве. Координаты вектора

9 Базис на плоскости и в пространстве.
Координаты вектора
Условия коллинеарности и компланарности
векторов в координатной форме выглядит
следующим образом:
1. Два вектора коллинеарны, если
a || b
a b
a1 a2 a3
b1 b2 b3
2. Три вектора компланарны, если
a1
a2
a3
b1
c1
b2
c2
b3 0
c3

10. Базис на плоскости и в пространстве. Координаты вектора

10Базис на плоскости и в пространстве.
Координаты вектора
Пример. Даны четыре вектора:
a1 1; 2; 0 , a2 1; 2;1 , a3 2;1; 1 , b 3; 2; 7
Показать, что три первых вектора образуют базис
в трехмерном пространстве и разложить
четвертый вектор по этому базису.
1 2 0
1 2 1
2 1 1
A11
2
1
2 ( 1) 1 1 3
1 1
1
31
A12 ( 1)
1(1 ( 1) 1 2) 3
2 1
1 ( 3) 2 3 9
Δ≠0, а значит это базис.

11. Базис на плоскости и в пространстве. Координаты вектора

11Базис на плоскости и в пространстве.
Координаты вектора
b 3; 2; 7
Разложим четвертый вектор по этому базису:
b x a1 y a2 z a3
Запишем в координатном виде:
3
1
1
2
2 x 2 y 2 z 1
7
0
1
1

12. Базис на плоскости и в пространстве. Координаты вектора

12Базис на плоскости и в пространстве.
Координаты вектора
Запишем систему уравнений:
3 x y 2 z
2 2x 2 y z
7
y z
1 1 2
A 2 2 1
0 1 1
x y 2z 3
2 x 2 y z 2
y z 7
3
f 2
7

13. Базис на плоскости и в пространстве. Координаты вектора

13Базис на плоскости и в пространстве.
Координаты вектора
Осталось решить систему из 3-х уравнений на
3-и неизвестные:
1 1 2
2 2 1
0 1 1
3 1 1 2
2 0 4 5
7 0 1 1
3
8
7
1 1 2
0 1 1
0 4 5
3 1 1 2
7 0 1 1
8 0 0 9
3
7
36

14. Базис на плоскости и в пространстве. Координаты вектора

14Базис на плоскости и в пространстве.
Координаты вектора
x y 2 z 3
y z 7
9 z 36
x y 2 z 3
y 4 7
z 4
x 2
y 3
z 4
b 2; 3;4
x ( 3) 2 4 3
y 3
z 4

15. Скалярное произведение векторов.

15
Скалярное произведение
векторов.
Скалярным произведением векторов называют сумму
произведений их координат:
a·b=a1·b1+a2·b2+a3·b3
Скалярным
произведением
векторов
называют
произведение длин этих векторов на косинус угла между
ними:
a·b=|a|·|b|·cos(α)
Скалярное произведение векторов можно еще представить:
где
проекция вектора а на вектор b.

16. Скалярное произведение векторов.

16
Скалярное произведение
векторов.
С помощью скалярного произведения можно вычислить:
Длину вектора:
a a a a
2
1
2
2
2
3
Расстояние между двумя точками:
AB AB
xB xA 2 yB y A 2 zB z A 2
Косинус угла между двумя векторами:
ax bx a y by az bz
a b
cos( )
a b
ax2 a y2 az2 bx2 by2 bz2

17. Скалярное произведение векторов.

17
Скалярное произведение
векторов.
Условие
перпендикулярности
векторов:
a b
2
(ортогональности)
n cos( ) 0
a b 0 a1 b1 a2 b2 a3 b3 0, a 0, b 0 .

18. Свойства скалярного произведения векторов.

18
Свойства скалярного
произведения векторов.
1. a b b a ;
2. a b c a b a c ;
3.
4.
a b c a c b c ;
a b a b a b ;
5. a a a ;
2
6. a b 0 a b
a 0, b 0
(критерий ортогональности векторов);
7. Работа силы F , действующей на материальную точку
при перемещении её из начала в конец вектора s
вычисляется по формуле A F s (физический смысл).

19. Векторное произведение.

19
Векторное произведение.
Векторным произведением двух векторов a и b
называется вектор c такой, что:
1. c a b sin - модуль вектора с равен
площади параллелограмма, построенного на
векторах a и b;
2. c a , c b ;
3. Тройка векторов a , b , c правая.

20. Векторное произведение.

20
Векторное произведение.
Обозначение:
Координаты вектора
i
c ax
j
ay
bx
by
c c , c , c
c a,b , c a b
k
ay
az
by
bz
x
y
z
вычисляются по формуле:
az
ax
i
bz
bx
ax
az
j
bx
bz
ay
k.
by

21. Свойства векторного произведения.

21
Свойства векторного
произведения.
1. a b b a ;
2. a b c a b a c ;
3.
4.
a b c a c b c ;
a b a b a b ;
5. a a 0;
6. a b 0 a || b
критерий коллинеарности векторов.

22. Смешанное произведение векторов.

22
Смешанное произведение
векторов.
a b c
Смешанным произведением векторов
a , b , c
или
называется число:
ax
a b c a b c a b c bx
ay
by
az
bz ,
cx
cy
cz
Абсолютная величина смешанного произведения векторов
a , b , c равна объему параллелепипеда построенного
на этих векторах.
ax a y az
V a , b , c bx
by
bz .
cx
cy
cz

23. Свойства смешанного произведения.

23
1.
2.
3.
Свойства смешанного
произведения.
a , b , c b , a , c , a , b , c a , c , b ;
a , b , c a , b , c a , b , c a , b , c ;
a , b , c 0 a , b , c - компланарны.

24. Примеры.

24
Примеры.
Найти угол между векторами p и q, если p=2m+3n, q=m+2n,
|m|=2, |n|=3, а угол между векторами m и n равен π/3.
Напомним, что:
вычислим
p q
p q
cos( pˆ q)
p q
p, q
и
p q 2m 3n m 2n 2m m 3n m 4m n 6n n
2 m 7m n 6 n 2 4 7m n 6 9 7 m n 62
2
2
1
m n m n cos( ) 2 3 3
3
2

25. Примеры.

25
Примеры.
p q 7m n 62 7 3 62 83
Теперь вычислим длину наших векторов:
p
2m 3n 2m 3n
4 m 12m n 9 n
2
2
4 4 12 3 9 9 16 36 81 133
q
m 2n m 2n
m 4m n 4 n
2
4 4 3 4 9 4 12 36 52
2

26. Примеры.

26
Примеры.
В результате получим:
p 133
q 52
p q 83
83
83
83
cos( pqˆ )
0,998
133 52
6916 83,16
( pq) arccos( 0,998) 3,6
0
50

27. Примеры.

27
Примеры.
Найти векторное произведение векторов
a 3,2, 1
b 1,0,2
i
j k
2 1
3 1
3 2
c a b 3 2 1
i
j
k
0 2
1
2
1 0
1 0 2
4i 5 j 2k
c 4,5, 2

28. Примеры.

28
Примеры.
Вычислить смешанное произведение векторов
a 3,2, 1 b 1,0,2 c 4,5, 2
3 2
a b c 1
4
0
1
2 1 1
5 2
2
1
5 2
( 1) 2
1 ( 4 5) 2 ( 15 8) 1 2 ( 23) 45
3 2
4
5

29. Аналитическая геометрия на плоскости.

29 Аналитическая геометрия на
плоскости.
1. Расстояние d между точками M1(x1,y1) и M2(x2,y2)
на плоскости:
2
2
d
x2 x1 y2 y1 .
2. Деление отрезка в заданном отношении λ. Даны
точки M1(x1,y1) и M2(x2,y2). Тогда координаты точки
N(x,y), делящей отрезок М1М2 в отношении M 1 N
NM 2
определяется по формуле:
При λ=1:
x1 x2
x
,
1
y1 y2
y
1
x1 x2
x
,
2
y1 y2
y
2

30. Аналитическая геометрия на плоскости.

30 Аналитическая геометрия на
плоскости.
3. Основные виды уравнений прямой на плоскости:
а) общее уравнение:
l : Ax By C 0,
n A, B - нормальный вектор прямой, n l;
б) уравнение прямой с угловым коэффициентом
l : y kx b, k - угловой коэффициент, равный
тангенсу угла α, который образует прямая с
положительным направлением оси Ox, b – ордината
точки пересечения прямой с осью Oy;

31. Аналитическая геометрия на плоскости.

31 Аналитическая геометрия на
плоскости.
x y
l:
1,
в) уравнение прямой в отрезках
a b
где а – абсцисса, b – ордината точек пересечения
прямой с осями Ох и Оу соответственно;
г) уравнение прямой, проходящей через две точки
M1(x1,y1) и M2(x2,y2)
x x
y y
l:
1
x2 x1
1
y2 y1
;
д) уравнение прямой, проходящей через данную
точку M0(x0,y0) в данном направлении
l : y y0 k x x0 , k - угловой коэффициент.

32. Аналитическая геометрия на плоскости.

32 Аналитическая геометрия на
плоскости.
4. Взаимное расположение двух прямых y=k1x+b1 и y=k2x+b2:
а) угол между прямыми:
k 2 k1
tg
,
1 k1 k 2
где k1 и k2 – угловые коэффициенты этих прямых;
– угол, на который нужно повернуть первую
прямую против часовой стрелки до совпадения со
второй прямой;

33. Аналитическая геометрия на плоскости.

33 Аналитическая геометрия на
плоскости.
б) признак параллельности двух прямых: k1=k2;
1
в) признак перпендикулярности двух прямых: k 2 .
k1
5. Расстояние от точки M0(x0,y0) до прямой
Ax+By+C=0 находиться по формуле:
d
Ax0 By 0 C
A2 B 2
.

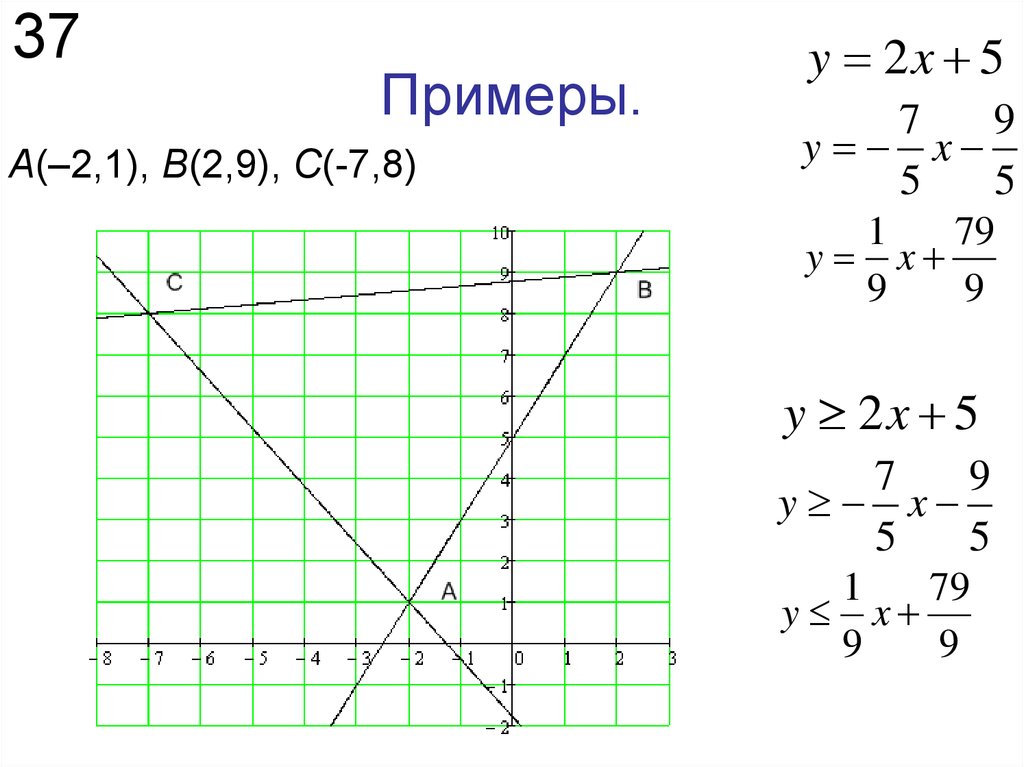
34. Примеры.

34
Примеры.
Даны координаты вершин треугольника АВС: А(–2,1), В(2,9),
С(-7,8). Hайти: 1) систему неравенств, определяющих
множество точек треугольника АВС; 2) угол С в радианах с
точностью до двух знаков; 3) уравнение высоты AD и ее
длину; 4) уравнение медианы СE и координаты точки F
пересечения этой медианы с высотой AD; 5) уравнение
окружности, для которой высота AD есть диаметр.
Решение:
1) Каждая
прямая
разбивает
плоскость
на
две
полуплоскости: под прямой и над прямой – это
обозначается в уравнении прямой знаком неравенства.
Построим прямые проходящие через точки А, В и С по
x x1
y y1
формуле:
l:
;
x2 x1
y2 y1

35. Примеры.

35
Примеры.
А(–2,1), В(2,9), С(-7,8)
x 2 y 1
,
2 2 9 1
y 2x 5
x 2
y 1
,
7 2 8 1
7
14
y x 1,
5
5
l:
x x1
y y1
;
x2 x1 y2 y1
1
1
( x 2) ( y 1), 2( x 2) y 1
4
8
1
1
7
( x 2) ( y 1), ( x 2) y 1
5
7
5
7
9
y x
5
5

36. Примеры.

36
Примеры.
А(–2,1), В(2,9), С(-7,8)
y 2x 5
x 2
y 9
,
7 2 8 9
1
2
y x 9,
9
9
l:
x x1
y y1
;
x2 x1 y2 y1
7
9
y x
5
5
1
( x 2) 1( y 9),
9
1
79
y x
9
9
1
( x 2) y 9,
9

37. Примеры.

37
Примеры.
А(–2,1), В(2,9), С(-7,8)
y 2x 5
7
9
y x
5
5
1
79
y x
9
9
y 2x 5
7
9
y x
5
5
1
79
y x
9
9

38. Примеры.

38
Примеры.
2) угол С в радианах с точностью до двух знаков;
А(–2,1), В(2,9), С(-7,8)
Уравнения АС и ВС имеют вид:
7
9
1
79
y x
y x
9
9
5
5
Соответственно коэффициенты КА=-7/5, КВ=1/9.
k 2 k1
Мы знаем, что
tg
,
1 k1 k 2
7 1
63 5
68 38
68 45
34
5
9
45
ˆ
tgC
:
7
45 45
45 38
19
7 1
1
1
45
5 9

39. Примеры.

39
Примеры.
34
34
ˆ
ˆ
tgC , C arctg 2,08
19
19
3) уравнение высоты AD и ее длину;
Вспомним признак перпендикулярности прямых: k 1 .
k1
1
В нашем случае
k1 ,
9
Т.е. К=-9, тогда уравнение прямой будет записываться по
формуле:
А(–2,1)
y y0 k x x0
y 1 9( x 2)
AD : y 9 x 17

40. Примеры.

40
Примеры.
Расстояние от точки до прямой вычисляется
d
Ax0 By 0 C
A2 B 2
А(–2,1)
1
79
y x
9
9
1
79
x y
0
9
9
.
1
79
2 9 79
( 2) 1 1
9 9 9 9
AD 9
2
1 81
1
2
1
81 81
9
68
68
9
AD
7,51
82
82
9

41. Примеры.

41
Примеры.
4) уравнение медианы СE и координаты точки F пересечения
этой медианы с высотой AD.
Чтобы найти уравнение медианы СЕ, определим сначала
координаты точки Е, которая является серединой стороны
АВ.
x1 x2
x
,
2
y1 y2
y
2
А(–2,1), В(2,9)
2 2
x
0,
2
1 9
y
5
2

42. Примеры.

42
Примеры.
С(-7,8), Е(0,5)
l:
x x1
y y1
;
x2 x1 y2 y1
x 7 y 8 1
1
CE :
;
( x 7) ( y 8);
0 7 5 8 7
3
3
3
CE : y 8 ( x 7); y 8 x 3;
7
7
3
CE : y x 5.
7

43. Примеры.

43
Примеры.
Для нахождения координат точки пересечения медианы и
высоты, решим систем уравнений составленную их
уравнения медианы и уравнения высоты:
3
CE : y x 5 AD : y 9 x 17
7
3
y x 5
,
7
y 9 x 17
3
9 x 17 x 5 63 x 119 3 x 35
,
,
7
y 9 x 17
y 9 x 17
77
60 x 154 x 30
,
y 9 x 17 y 61
10

44. Примеры.

44
Примеры.
5) уравнение окружности, для которой высота AD
68
34
есть диаметр. AD 68
R
82
AD : y 9 x 17
2 82
82
1
79
BC : y x
9
9
79
1
9 x 17 x 79 81x 153
y 9 x 17 x
9
9
1
79 ,
,
y 1 x 79 ,
y x
1
79
y x
9
9
9
9
9
9
116
116
x
x
82 x 232
41
41
,
y 1 x 79 ,
116 3239
347
y
y
9
9
41 9
41

45. Примеры.

45
Примеры.
Осталось записать уравнение окружности
( x x0 ) ( y y0 ) R
2
116
x0 41
347
y0
41
2
2
34
R
82
2
2
116
347
578
x
y
41
41
41