Similar presentations:
Модели, описываемые системами двух автономных дифференциальных уравнений
1. МОДЕЛИ, ОПИСЫВАЕМЫЕ СИСТЕМАМИ ДВУХ АВТОНОМНЫХ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ.
2. Фазовая плоскость
• качественное моделирование свойств биологическихсистем получено на моделях из двух
дифференциальных уравнений с помощью метода
фазовой плоскости.
dx
P( x , y ),
dt
dy
Q( x , y ).
dt
Каждая точка М этой
плоскости
соответствует
определенному
состоянию системы.
3. Фазовый портрет
• Для изображения фазовогопортрета необходимо
построить векторное поле
направлений траекторий
системы в каждой точке
фазовой плоскости. Задавая
приращение t>0, получим
соответствующие
приращения x и y из
выражений:
• x=P(x,y) t,
• y=Q(x,y) t.
dy Q( x , y )
dx P( x , y )
y
y
x
y
y
x
x
x
P(x,y)>0,
Q(x,y)>0
P(x,y)<0,
Q(x,y)<0
y
y
x
y
y
x
x
P(x,y)>0,
Q(x,y)<0
x
P(x,y)<0,
Q(x,y)>0
4. Метод изоклин
• Для построения фазового портрета пользуются методомизоклин – на фазовой плоскости наносят линии, которые
пересекают интегральные кривые под одним определенным
углом.
• Значение А представляет собой тангенс угла наклона
касательной к фазовой траектории и может принимать значения
от – до + .
Q( x , y )
A
P( x , y )
• Это уравнение определяет в каждой точке плоскости
единственную касательную к соответствующей интегральной
кривой за исключением точки, где P (x,y) = 0, Q (x,y) = 0,
называемой – особой точкой.
5. Главные изоклины
• dy/dx=0, P(x,y)=0 – изоклина горизонтальных касательных и• dy/dx= , Q(x,y)=0 – изоклина вертикальных касательных.
• Построив главные изоклины и найдя точку их пересечения (x,y),
координаты которой удовлетворяют условиям:
P( x , y ) 0, Q( x , y ) 0,
6. Фазовые траектории системы
• это проекцииинтегральных кривых
в пространстве всех
трех измерений x, y, t
на плоскость x, y
• если условия
теоремы Коши
выполнены, то через
каждую точку
пространства x, y, t
проходит
единственная
интегральная кривая
7. Устойчивость стационарного состояния
• Для состояния равновесияdx
0;
dt
dy
0
dt
• Состояние равновесия
устойчиво, если для любой
заданной области отклонений от
состояния равновесия ( ) можно
указать область ( ),
окружающую состояние
равновесия и обладающую тем
свойством, что ни одна
траектория, которая
начинается внутри области ,
никогда не достигнет границы .
8. Линейные системы
dxdy
ax by ,
cx dy
dt
dt
A aA bB,
B cA dB.
t
x Ae , y Be
a
c
a d
( a d )2 4( ad bc )
1,2
2
4
d
d
1 ,
2
dt
dt
b
d
t
0
x c11e 1 t c12 e 2 t ,
y c 21e 1 t c 22 e
x y,
2t
.
x y.
9. Корни λ1, λ2
λ1, λ2 – действительны и одного знакаλ1, λ2 – комплексные сопряженные
один из характеристических корней которой равен нулю
λ1, λ2 – действительны и разных знаков
Особая точка типа седло
10. ИССЛЕДОВАНИЕ УСТОЙЧИВОСТИ СТАЦИОНАРНЫХ СОСТОЯНИЙ
• Ляпунов показал, что в большом числе случаеванализ устойчивости стационарного состояния
нелинейной системы можно заменить анализом
устойчивости системы, линеаризованной в
окрестности стационарного состояния.
P ( x , y ) 0,
Q ( x , y ) 0.
dy Q( x, y )
.
dx P( x, y )
x x ,
y y .
d x d
P ( x , y ),
dt dt
d y d
Q( x , y ).
dt dt
d
P( x , y ) a b ( p11 2 2 p12 p 22 2 ...) ...,
dt
разложим правые части
d
Q( x , y ) c d (q11 2 2q12 q 22 2 ...) ..., уравнений в ряд Тейлора
dt
11.
• Получим систему первого приближения1, 2
(a d ) (a d ) 2 4(ad bc)
2
d
a b ,
dt
d
c d .
dt
• если оба корня имеют отрицательную действительную
часть, то состояние равновесия устойчиво;
• если хотя бы один корень имеет положительную
действительную часть, то состояние равновесия
неустойчиво.
• Если действительные части обоих корней
характеристического уравнения равны нулю или если один
корень равен нулю, а другой отрицателен, то необходимо
рассматривать члены более высокого порядка малости в
разложении в ряд Тейлора правых частей уравнений.
12. Грубые системы
• В случае, когда оба корня характеристического уравненияимеют отличные от нуля действительные части, уравнение
первого приближения определяют не только устойчивость
стационарного состояния, но и характер фазовых траекторий в
достаточно малой его окрестности.
• здесь возможны пять типов грубых состояний равновесия:
устойчивый узел, неустойчивый узел, устойчивый фокус,
неустойчивый фокус и седло.
[ Px ( x , y ) Qy ( x , y )]
Px ( x , y ) Qx ( x , y )
Py ( x , y ) Q y ( x , y )
13. Кинетические уравнения
• гипотетическая химическая реакцияdx
k 0 k1 xy,
dt
dy
k1 xy k 2 y ,
dt
dB
k 2 y.
dt
x
dx
0,
dt
dy
0.
dt
k 0 k1 x y 0,
k1 x y k 2 y 0.
k2
k
, y 0
k1
k2
Координаты
особой точки
2
k1k0
1 k1k0
1, 2
4k0 k1
2 k2
k2
14. Модель «хищник-жертва»
dxx( x xy y ),
dt
dy
y ( y yx x).
dt
x
y
x
,
y
x
.
y
y y
d
dt
x
d y x
dt
y
x - жертва и y - хищников
x = 4,
xy = 0,3,
y = yx = 0,4
1, 2 i x y
x =2,
xy = 0,3,
y = yx = 0,4
15. ПРОБЛЕМА БЫСТРЫХ И МЕДЛЕННЫХ ПЕРЕМЕННЫХ
задача моделирования
заключается в том, чтобы
построить модель
явления, содержащую
возможно меньшее число
переменных и
произвольных
параметров, и в то же
время правильно
отражающую свойства
явления.
учет временной иерархии
процессов позволяет
сократить число
дифференциальных
уравнений.
16. Средние, быстрые и медленные времена
dxP ( x, y, z ),
dt
dy
Q ( x, y, z ),
dt
dz
F ( x, y, z ).
dt
Tx Ty Tz
.
P(x, y, z*) =0
x x ( y, z )
dy
Q( x ( y, z ), y, z ).
dt
Процесс квазистационарный
dx
P ( x, y, z * ),
dt
dy
Q ( x, y , z * ).
dt
17. Бифуркации динамических систем
• Здесь x – вектор переменных, - вектор параметровdx
F ( x, ).
dt
F ( x, ) 0
• Зафиксируем некоторое = *, и рассмотрим фазовые портреты
системы при данном значении параметра, а также при > * и
< *.
• Фазовые портреты топологически эквивалентны, если
существует невырожденное непрерывное преобразование
координат, которое переводит все элементы одного
фазового портрета в элементы другого.
18. Бифуркация седло-узел
(а) - < * - устойчивый узел седло или узел, (б) - = * - происходитслияние с образованием седло-узел,
(в) > * положение равновесия исчезает.
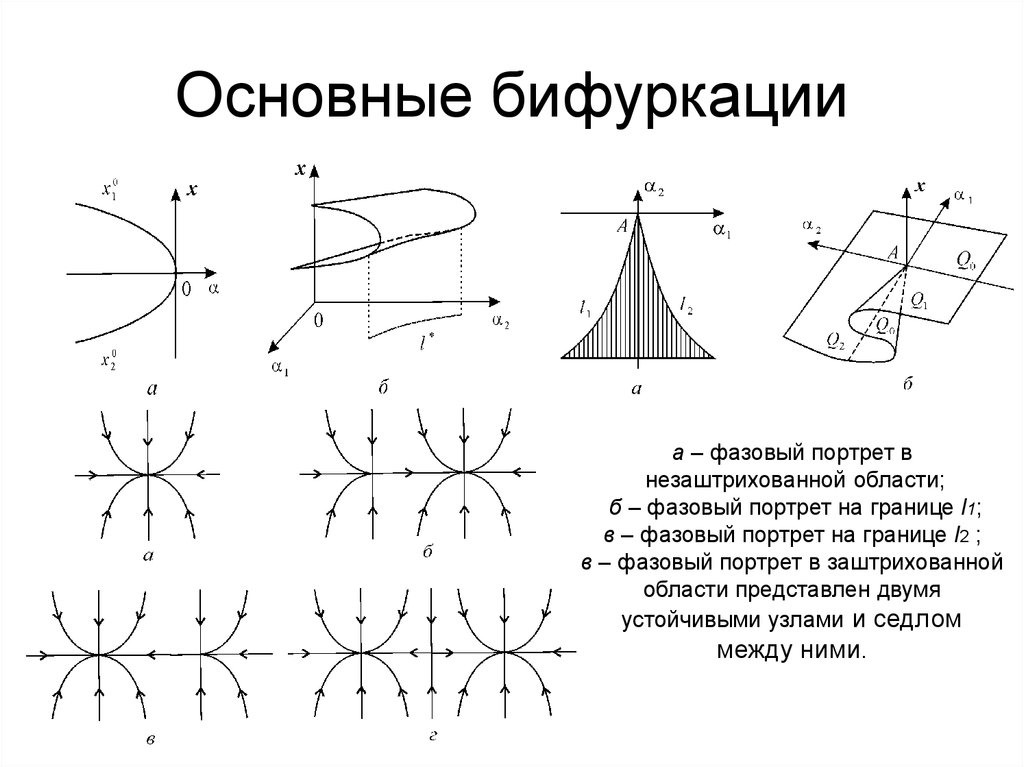
19. Основные бифуркации
а – фазовый портрет внезаштрихованной области;
б – фазовый портрет на границе l1;
в – фазовый портрет на границе l2 ;
в – фазовый портрет в заштрихованной
области представлен двумя
устойчивыми узлами и седлом
между ними.
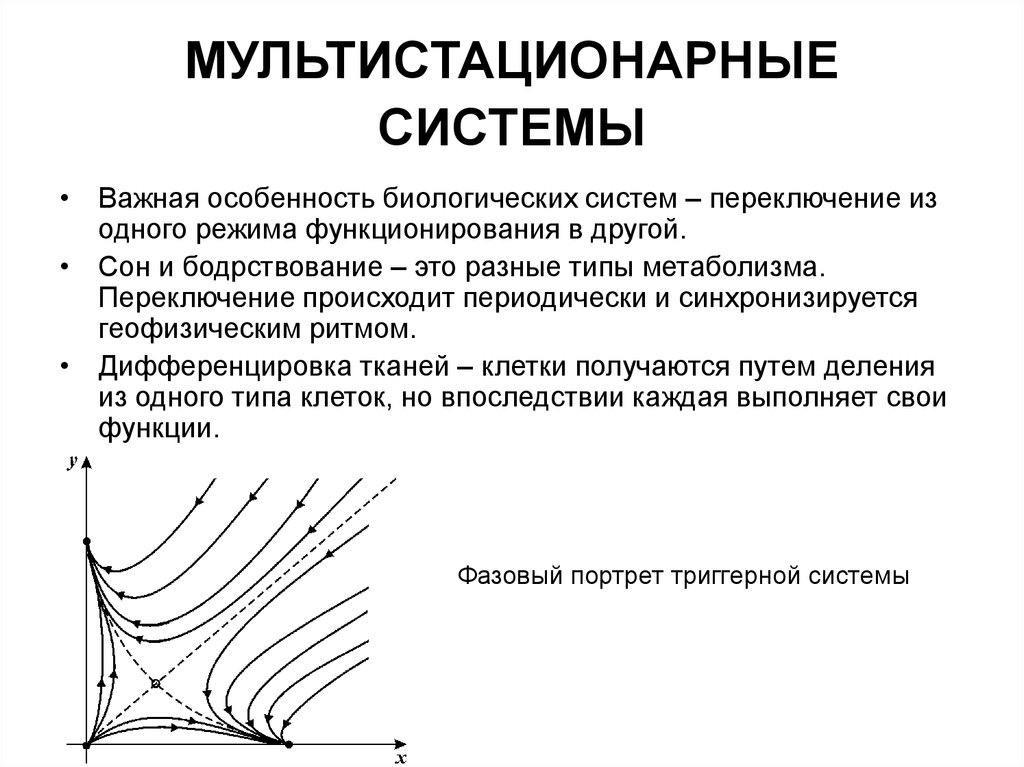
20. МУЛЬТИСТАЦИОНАРНЫЕ СИСТЕМЫ
• Важная особенность биологических систем – переключение изодного режима функционирования в другой.
• Сон и бодрствование – это разные типы метаболизма.
Переключение происходит периодически и синхронизируется
геофизическим ритмом.
• Дифференцировка тканей – клетки получаются путем деления
из одного типа клеток, но впоследствии каждая выполняет свои
функции.
Фазовый портрет триггерной системы
21. Уравнения триггерных систем
dx1 x x x ax 2 ,
1 1 2
1
dt
dx
2 x x x ax 2 .
2 1 2
2
dt
x1=x2=0 – неустойчивый узел;
x1 x 2
x1
1
1 a
1
, x2 0
a
x1 0, x 2
1
,
a
– седло
– устойчивый узел;
– устойчивый узел
dx
y,
dt
dy
ay b( x x 3 )
dt
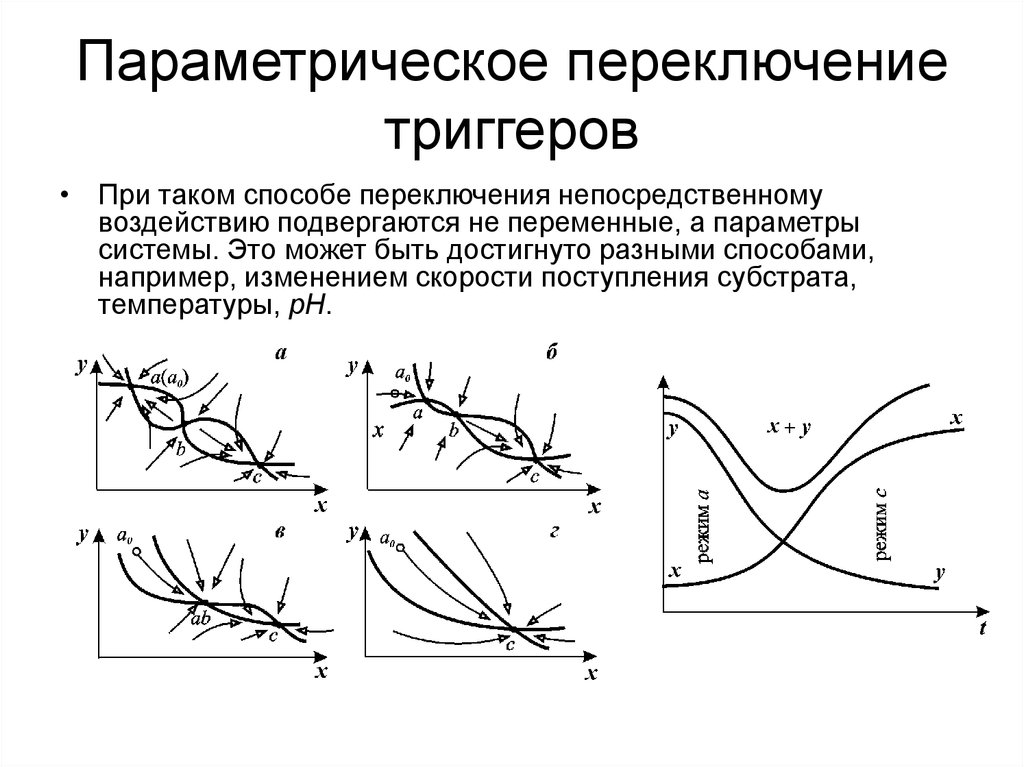
22. Параметрическое переключение триггеров
• При таком способе переключения непосредственномувоздействию подвергаются не переменные, а параметры
системы. Это может быть достигнуто разными способами,
например, изменением скорости поступления субстрата,
температуры, рН.
23. КОЛЕБАНИЯ В БИОЛОГИЧЕСКИХ СИСТЕМАХ
Устойчивый (а) и неустойчивые (б и в) предельные циклы на фазовой плоскостиdx
y x [1 ( x 2 y 2 )],
dt
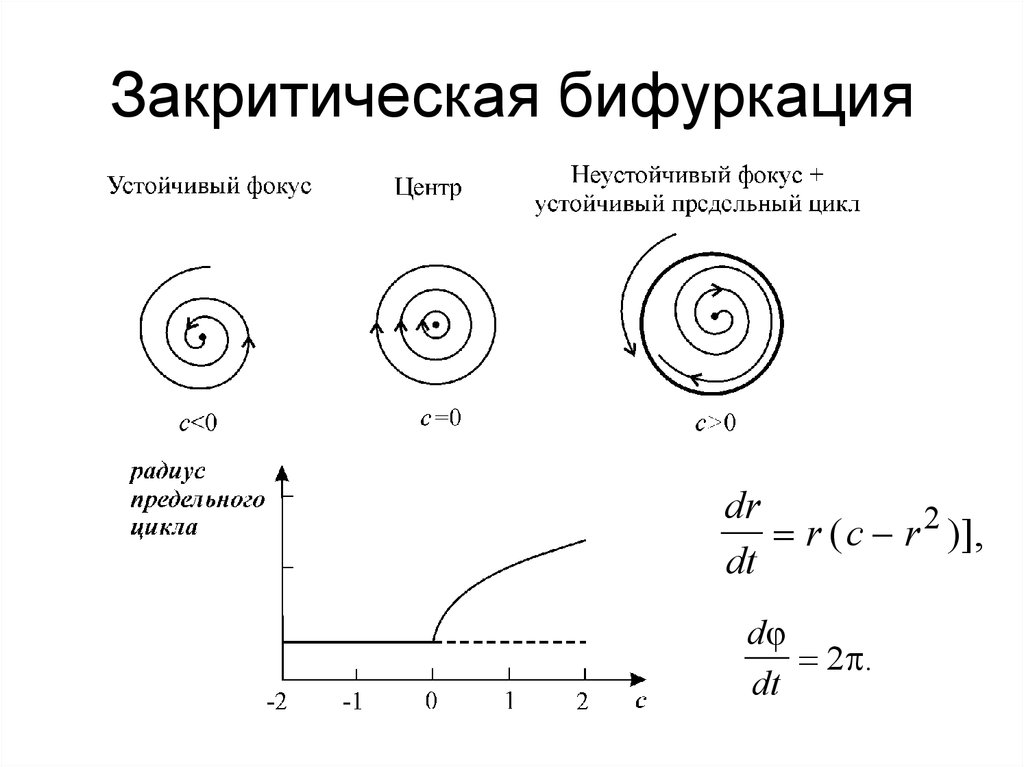
24. Закритическая бифуркация
drr ( c r 2 )],
dt
d
2 .
dt
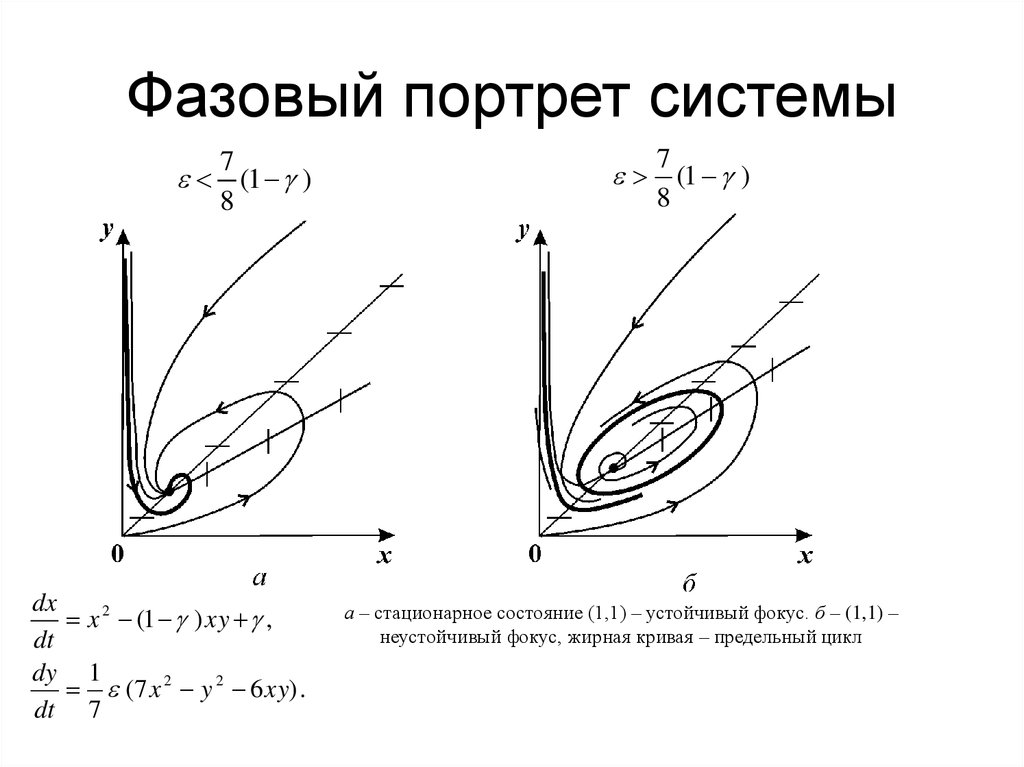
25. Фазовый портрет системы
7(1 )
8
dx
x 2 (1 ) xy ,
dt
dy 1
(7 x 2 y 2 6 xy) .
dt 7
7
(1 )
8
а – стационарное состояние (1,1) – устойчивый фокус. б – (1,1) –
неустойчивый фокус, жирная кривая – предельный цикл
26. ДИНАМИЧЕСКИЙ ХАОС Лоренца
x y x,y rx y xz,
z xy bz.
27. Анализ устойчивости траекторий
• Поиск «хаотического аттрактора».Вид проекций фазовой траектории
на странном аттракторе в
системе Ресслера.
x ( x y ),
y x y,
z z ( x ).
28. Линейный анализ устойчивости траекторий
• Для общей характеристики устойчивости траекториипо отношению к возмущению вдоль i-го собственного
вектора используют величину, называемую
характеристическим показателем Ляпунова:
1
i lim
ln y i (t ) .
t t t 0
• Таким образом – это усредненное вдоль
исследуемой траектории значение действительной
части собственного значения i матрицы
линеаризации.
29. Разные типы аттракторов
Биологические системыпо своей природе являются
диссипативными.
Поэтому их модели
принципиально
нелинейны.
V (t ) V (t 0 ) exp[( t t 0 )divF( x(t ))]
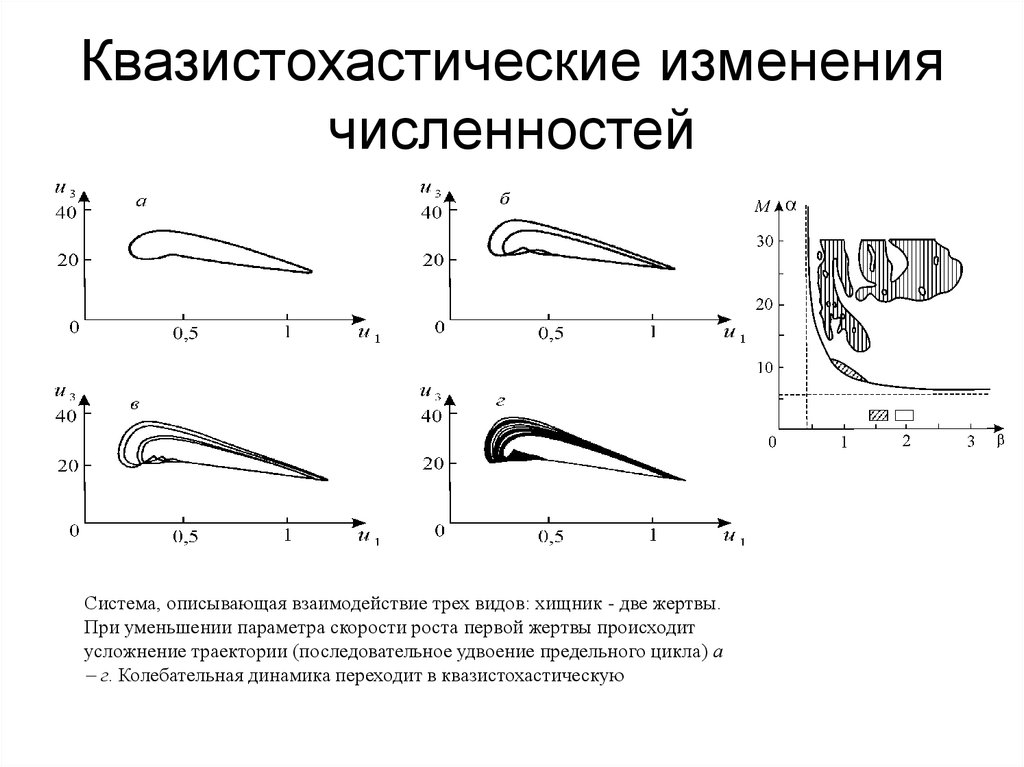
30. Квазистохастические изменения численностей
Система, описывающая взаимодействие трех видов: хищник - две жертвы.При уменьшении параметра скорости роста первой жертвы происходит
усложнение траектории (последовательное удвоение предельного цикла) а
г. Колебательная динамика переходит в квазистохастическую
























 mathematics
mathematics








