Similar presentations:
Дифференциальные уравнения и системы
1.
ТомскийТомский политехнический
политехнический университет
университет
Доцент, к.ф.м.н.
Богданов Олег Викторович
Дифференциальные уравнения
и системы. (Пр.1)
2016
2. Виды дифференциальных уравнений
Уравнения 1-го порядка1. Уравнения с разделяющимися
переменными
2. Однородные уравнения
3. Линейные уравнения
4. Уравнения Бернулли
5. Уравнения в полных
дифференциалах
Уравнения высших порядков
1. Уравнения, допускающие
понижение порядка
2. Линейные уравнения
высших порядков
а) однородные
б) неоднородные
в) неоднородные уравнения
с правой частью
специального вида
Системы дифференциальных уравнений
3. Дифференциальные уравнения 1-го порядка
Обыкновенным дифференциальным уравнением называетсяуравнение, которое связывает независимую переменную,
искомую функцию и производные искомой функции.
П о р я д о к дифференциального уравнения определяется
порядком старшей производной, входящей в уравнение.
Дифференциальным уравнением 1-го порядка называется уравнение,
связывающее независимую переменную, искомую функцию и ее
первую производную
y = f ( x; y )
y y x y,
y '' 4 y cos 2 x
(5 x 4 y )dx (3x 2 y )dy 0
y ''' 2 y '' 3 y ' 2 x e 2 x
'
4.
Формы записи дифференциального уравнения 1-го порядка:y = f ( x; y )
явная,
F ( x; y; y ) = 0
неявная,
M ( x; y ) dx N ( x; y ) dy = 0
дифференциальная.
Например:
y = y 2 2 y
явная,
x 2 y 2 xy 1 = 0 неявная,
( x 2 y 2 )dy (2 xy 1)dx = 0
дифференциальная.
Нахождение решения дифференциального уравнения
называется его интегрированием
Метод решения уравнения определяется типом уравнения.
5.
Р е ш е н и е м дифференциального уравнения называется любаяy =которая
y ( x), при подстановке в уравнение
дифференцируемая функция
обращает его в тождество.
Общим интегралом уравнения называется его решение,
полученное в неявном виде.
Каждое дифференциальное уравнение первого порядка имеет
бесконечное множество решений.
Все это множество можно описать одной функцией, которая называется
общим решением или общим интегралом дифференциального уравнения.
Из этого множества можно выбрать конкретное (частное) решение,
если задать начальное условие.
Н а ч а л ь н ы м у с л о в и е м для уравнения первого порядка
является задание значения искомой функции при заданном значении
независимой переменной, т.е.
y ( x0 ) = y0 .
О б щ и м решением дифференциального уравнения 1-го порядка
называется функция
y = y ( x; C ),
З а д а ч а К о ш и -- нахождение частного решения,
удовлетворяющего заданному начальному условию.
6. Основные типы уравнений 1-го порядка
Уравнение с разделенными переменными – это уравнение видамножителем при
является функция
f ( x) dx g ( y ) dy = 0,
dx является функция
x,
y.
а множителем при
Решение таких уравнений заключается в почленном интегрировании
левой и правой его частей
f ( x) dx g ( y ) dy = C.
1. cos x dx = y dy.
cos x dx =
sin x C =
y dy.
2 3/2
3
y , y = [ (sin x C )]2/3.
3
2
dy
7. Уравнения с разделяющимися переменными
Это уравнения видаy = f1 ( x) f 2 ( y )
или
f1 ( x)
y =
f2 ( y)
или
f2 ( y)
y =
.
f1 ( x)
В уравнении с разделяющимися переменными правая часть
представляет собой, или может быть представлена в виде
произведения (или отношения) двух функций, одна из которых
зависит только от x , а другая -- только от
y.
Если уравнение изначально задано в дифференциальной форме
M ( x; y ) dx N ( x; y ) dy = 0,
то оно будет уравнением с разделяющимися переменными, если его
можно представить в виде
f1 ( x) f 2 ( y ) dx g1 ( x) g 2 ( y ) dy = 0.
8.
1. y = (3 y 5)ctg x.1) Заменяем
y :
y = dy/dx.
dy
= (3 y 5)ctg x,
dx
2) Умножаем обе части уравнения на
dx
dy = (3 y 5)ctg x dx.
3) Делим на "стоящую не у своего дифференциала" функцию
dy
= ctg x dx.
3y 5
4) Интегрируем обе части уравнения
1
ln | 3 y 5 |= ln | sin x | ln C
3
(3 y 5),
dy
3 y 5 = ctg x dx C ,
3 3 y 5 C sin x - общий
интеграл уравнения
9.
2. 7x2 y
y 2 x = 0.
a x y = a x a y
1) Используя свойство показательной функции
y dy ,
и, заменяя
получим
dx
2x
2) Переносим
y
dx
в правую часть, умножаем на
dy
7 7 2 x.
dx
x2
dy
7 7 2 x = 0.
dx
x2
7 dy = 7
y
y
x2
и делим на
2 x dx.
3) Интегрируем и получаем общий интеграл
7
y
dy = 7
Или, окончательно
x2
y
7
7
C
=
.
ln 7 ln 7 ln 7
d ( x ),
2
y
7 =7
x2
x2
C.
x2
7 .
10.
3. 6 xdx 6 ydy = 3x 2 ydy 2 xy 2dx.dx
1) Собираем слагаемые с
dy
одну часть уравнения, а слагаемые с
в другую.
6 xdx 2 xy 2 dx=6 ydy 3 x 2 ydy,
2) Выносим
dx
3) Выносим
2x
и
dy
и
3y
за скобки.
(6 x 2 xy 2 )dx = (6 y 3 x 2 y )dy,
за скобки и получаем
2 x (3 y 2 ) dx = 3 y (2 x 2 ) dy,
делим на произведение
(2 x 2 ) (3 y 2 ) т.е. функций,
«стоящих не у своих дифференциалов», и интегрируем
2x
3y
2x
3y
dx =
dy,
dx =
dy,
2
2
2
2
2 x
3 y
2 x
3 y
3
ln | x 2 2 |= ln | 3 y 2 | ln C.
x2 2 = C
2
Ответ:
(3 y 2 )3 .
11.
1 x24. y y
1 = 0.
2
1 y
1) y =
1 y
1 y2
dy
2) =
.
2
dx
y 1 x
2
y 1 x
2
.
1 y2
dx
3) dy =
.
2
y
1 x
4)
y dy
1 y
2
=
dx
1 x
4) 1 y 2 = arcsin x C.
y = 1 (arcsin x C ) 2
2
.
12.
Рассмотрим пример нахождения частного решения уравненияпо заданному начальному условию.
y 2 y y 2 = 0,
Решить задачу Коши
y (0) = 1/4.
1) Находим сначала общее решение уравнения:
y = y 2 2 y ,
dy
= ( y 2 2 y ),
dx
dy
= dx,
2
y 2y
dy
1 y 2
1
y 2 2 y = dx, 2 ln y = x 2 ln C.
Общее решение
y 2
= Ce 2x .
y
2) Определим значение константы
Подставим в общее решение значения
2
1 = Ce 2 x ,
y
2
= 1 Ce 2 x ,
y
C , исходя из начального условия.
x = 0, y = 1/4.
1/4 2
= C e0 , 9 = C.
1/4
C , подставляем в выражение для общего
3) Полученное значение
2
решения и записываем частное решение:
= 1 9e 2 x .
y
13. Однородные уравнения 1-го порядка
О п р е д е л е н и е. Дифференциальное уравнениеy = f ( x; y )
называется однородным, если его правая часть есть однородная функция своих
y
аргументов
f ( x; y ) = g .
x
Т.е. уравнение первого порядка будет являться однородным, если его
можно представить в виде
y
y = g .
x
14.
Как определить, что уравнение является однородным?Возможны две основные ситуации:
Первая:
y
e y/x
x
y
2. y x y = x arctg ( y/x) y = arctg ( y/x),
x
1. x y y = x x e y
3. x y y = ( x y ) ln
y =
y =
x y
y
y
y
y = 1 ln 1
x
x
x
x
Т.о. к однородным могут относиться уравнения, в которых
отношения
Вторая:
y
x
стоят под знаком какой-либо функции.
1. ( x y ) dy ( x y ) dx = 0.
x
dy x y
=
y = x
x
dx x y
x
y
x
y
x
y =
1 y/x
1 y/x
y
arctg ( y/x).
x
15.
2. ( x 2 y y 3 ) dx ( x3 xy 2 ) dy = 0.x2 y y3
( x y y ) ( x xy ) y = 0, y = 3
.
2
x xy
2
3
3
2
Все слагаемые числителя и знаменателя имеют третью степень,
разделим на
3
x
x2 y y3
3
3
x
y = x3
x
xy 2
3
3
x
x
y/x y/x
y =
2
1 y/x
3
Т.о. к однородным относятся дифференциальные уравнения, правая
часть которых является отношением двух многочленов, причем
все члены числителя и знаменателя имеют одинаковую
суммарную степень переменных.
Тогда после деления числителя и знаменателя дроби на
останутся только постоянные числа и отношения
в разных степенях.
y/x
x, x 2 , x 3
16.
РЕШЕНИЕ однородных уравненийОднородное уравнение сводится к уравнению с разделяющимися
переменными подстановкой
y
= t ( x).
x
y
= t ( x), y = t ( x) x, y = t x t ,
x
y2 3y
1. y = 2
2.
x
x
1) Делаем замену
Уравнение однородное и не требует никаких
предварительных преобразований
y
= t ( x) и все преобразования, которые необходимы
x
t x t = t 2 3t 2,
t x = t 2 2t 2,
2) Разделяем переменные.
dt
x = (t 2 2t 2),
dx
dt
dx
=
.
2
t 2t 2 x
17.
3) Интегрируем обе части выражения.dt
dx
=
(t 1)2 1 x ,
arctg (t 1) = ln | x | ln C
4) Делаем обратную замену
y
arctg ( 1) = ln (C x).
x
y = x [ tg (ln (C x) 1].
Получили общее решение уравнения.
18.
2. ( x 2 x y ) dy y 2 dx = 0.1) Разделим на
dx и выразим в явном виде
затем разделим числитель и
на
x2.
знаменатель правой части уравнение
y2
( x x y ) y y = 0, y = 2
,
x xy
2
y ,
2
y 2 /x 2
y =
.
y/x 1
y
= t ( x), y = t ( x) x, y = t x t ,
x
Уравнение
2
2
t
t
примет вид
t x t =
, t x =
t,
t 1
t 1
2
2
t t t
dt
t
t x =
,
x =
.
t 1
dx t 1
1
dx
(t 1) dt dx
3) Разделяем переменные
(
1
)
dt
=
,
= ,
t
x
t
x
2) Сделаем замену
4) Интегрируем
t ln | t |= ln | x | ln C ,
5) Делаем обратную замену
y
y
ln = ln(Cx),
x
x
19.
3. x y y =1) y =
x
y
cos
x
.
1
y
.
y x
cos
x
3)t x t =
Делаем замену
2)
1
t,
cos t
Разделяем переменные
4) cos t dt =
Уравнение однородное
dx
,
x
5) sin t = ln | x | C ,
y
= t , y = t x, y = t x t.
x
t x =
1
,
cos t
x
dt
1
=
,
dx cos t
dx
cos t dt =
x
Общий интеграл
y
sin = ln x C.
x
20. Линейные уравнения 1-го порядка
Уравнение 1-го порядка будет линейным, если искомая функцияи ее производная входят в уравнение в первых степенях и
не перемножаются.
Общий вид линейного уравнения
y P ( x ) y = Q ( x )
Всякое линейное уравнение прежде, чем применять методы его
решения, необходимо преобразовать к такому "классическому" виду.
Метод Бернулли (метод подстановки)
Этот метод позволяет с помощью подстановки
y = U ( x) V ( x)
сводить любое линейное уравнение к двум уравнениям с разделяющимися
переменными относительно функций
U (x) и
V (x).
21.
1. y 2 xy = xex2
1) Решение уравнения ищем в виде произведения двух функций
y = U V V U
y = U ( x) V ( x). Тогда
2) Подставляем выражение для функции и ее производной
в уравнение, группируем второе и третье слагаемые и выносим
общий множитель
U V V U 2 xUV = xe
3) Функцию
x2
U V U (V 2 xV ) = xe
V (x) ищем из условия, что выражение в скобках
равно нулю. Тогда получаем систему двух дифференциальных
уравнений для нахождения функций
U (x) и V (x)
V 2 x V = 0
x2
U V = x e .
x2
.
22.
4) Из 1-го уравнения находимфункцию V (x)
V 2 x V = 0,
5) Полученное выражение для
функции
V (x)
подставляем во 2-е уравнение
системы
U V = x e
x2
и находим вторую функцию
dV
= 2 x V ,
dx
dV
= 2 xdx,
V
2
ln V = x ,
V =e
x2
.
6) Записываем общее решение
x2
U e = x e
U = x,
x2
U (x)
,
U = x dx,
x2
U = C.
2
y = U ( x)V ( x) = e
x2
( x 2 /2 C ).
23.
2.( xy 1) ln x 2 y = 0.
Преобразуем уравнение к классическому виду
xy ln x ln x 2 y = 0.
y ' x ln x 2 y ln x
2
ln x
y
y
x ln x
x ln x
'
2y
1
y
= .
x ln x x
Делаем замену
y = U ( x) V ( x).
y = U V V U
24.
2UV 12V 1
= .
U V V U
= U V U V
x ln x x
x ln x x
Составляем систему
2
V
V = 0,
x ln x
dV
2
=
dx,
V
x ln x
ln V = 2 lnln x,
1
V= 2 .
ln x
Общее решение
2V
=0
V
x ln x
U V = 1/x.
U V = 1/x
1
=
,
2
ln x x
dU ln 2 x
=
,
dx
x
3
x
ln
U=
C
3
ln3 x
1
ln x
C
y ( x) = UV =
C 2 =
2 .
3
ln x
3
ln x
U
1
25. Уравнения Бернулли
Уравнение Бернулли- это уравнение видаk
y P( x) y = Q( x) y
где
k любое рациональное число, исключая случаи:
k = 0 ,k = 1
Уравнение Бернулли сводится к линейному, поэтому при решении конкретных
примеров уравнение Бернулли решается так же как и линейное , т.е.
рассмотренным выше методом Бернулли
2
tg x
1. y y =
y.
x
x
1) Решение уравнения ищем в виде:
y ( x) = U ( x)V ( x);
y = U V V U ,
26.
y2
tg x
y=
y.
x
x
3) Получаем систему
2
tg x
2)U V UV UV =
UV ,
x
x
2
tg x
U V U (V V ) =
UV .
x
x
2
4)V V ,
x
dV
2
= ,
dx
x
dV
2dx
=
,
V
x
ln V = 2 ln x,
5)U
1 tg x
1
=
U 2,
2
x
x
x
dU
= tg x U .
dx
dU
= tg x dx,
U
2 U = ln | cos x | 2 ln C
U ( x) = ln
1
V = 2.
x
6) Общее решение
2
V x V = 0
tg x
U V =
UV
x
y ( x) = U V =
1 2 C
.
2 ln
cos x
x
2
C
.
cos x
27.
2.y x y = (1 x)e x y 2 ,
y ( x) = U ( x)V ( x);
y = U V V U
Решить задачу Коши
U ' V U V ' x U V (1 x)e x y 2
U ' V U (V ' x V ) (1 x)e xU 2 V 2
dV
xV
dx
dV
x dx
V
dV
V xdx
x2
ln V
2
V e
V ' xV 0
'
x
2
2
U
V
(
1
x
)
e
U
V
U ' (1 x)e xU 2 V
x2
2
'
U
x
(
1
x
)
e
e
2
U
x2
x
dU
2
(
1
x
)
e
dx
2
U
dU
U 2 (1 x)e
2
x
2
y (0) = 1.
1
e
U
x2
x
2
( x
C
x2
)
2
dx e
( x
x2
)
2
x2
d (x )
2
1
U
e
x2
x
2
C
28.
Таким образом, общее решение исходного уравненияy=
e
e
x 2 /2
( x x 2 /2)
C
.
Для получения частного решения подставим начальное условие в
полученное общее решение
y (0) = 1
e0
1
1= 0
1=
1 C
e C
Частное решение:
y=
e
e
x 2 /2
( x x 2 /2)
C 0
= ex.
29.
З а м е ч а н и е. Дифференциальное уравнение может бытьЛинейным уравнением или уравнением Бернулли не только
x.
относительно переменной y , но и относительно
x P ( y ) x = Q( y ).
x ' P( y ) x = Q( y ) x k .
Решение уравнения ищем в виде:
x( y ) = U ( y )V ( y ), x = U V V U .
В остальном решение не отличается от стандартной ситуации.
y2
Например, уравнение
e (dx 2 x y dy ) = y dy
y,
не является линейным относительно
к линейному относительно
Делим на
dy
Получаем линейное уравнение
x.
y2
но может быть приведено
y2
e dx 2 x y e dy = y dy,
dx
y2
e
2 x y e = y,
dy
y2
x 2 y x = y e
y2
.
30. Уравнения в полных дифференциалах
УравнениеP ( x; y )dx Q ( x; y )dy = 0
является уравнением в полных
дифференциалах, если выполняется условие
P( x; y ) Q( x; y )
=
.
y
x
Если условие выполняется, то левая часть уравнения есть полный
дифференциал некоторой, пока неизвестной, функции
т.е.
P( x; y ) dx Q( x; y ) dy = d U ( x; y ).
Тогда, в соответствии с уравнением,
dU ( x; y ) = 0,
и поэтому общий интеграл уравнения в полных дифференциалах
запишется в виде
U ( x; y ) = C.
Таким образом, решение уравнения сводится к нахождению
функции U ( x, y )
U ( x, y ),
31.
U ( x; y ) сравним выражение для полногоДля нахождения функции
дифференциала функции двух переменных
U
U
dU =
dx
dy
x
y
с левой частью уравнения
dU P( x; y )dx Q( x; y )dy
Из этого сравнения видно, что
U
U
= P( x; y ),
= Q( x; y ).
x
y
Эти соотношения используются для нахождения функции
1. 3 x 2 y 2 y 3 dx ( x 3 2 x 3 y 2 ) dy = 0.
1) Проверяем условие
P Q
=
,
y x
3 x 2 y 2 y 3 = 3 x 2 2,
y
U ( x; y )
3
x 2 x 3 y 2 = 3 x 2 2.
x
Данное уравнение является уравнением в полных дифференциалах.
32.
U ( x; y ) . Для этого интегрируем поP( x; y ). Переменная y
2) Находим функцию
функцию
x
при этом считается постоянной
U ( x; y ) = 3 x 2 y 2 y 3 dx = y 3 x 2 dx 2 y dx 3 dx =
= x3 y 2 xy 3 x ( y ).
Здесь постоянная интегрирования записывается в виде функции
( y )
и эту функцию мы должны определить, используя для этого
второе соотношение
Полученное выражение для
U
= Q( x; y ),
y
U ( x; y ) : U ( x; y ) = x 3
дифференцируем по переменной
y 2 xy 3 x ( y )
y и приравниваем к функции
Q( x; y ).
33.
U y ( x; y ) = x3 y 2 xy 3 x ( y ) y = x3 2 x yQ( x; y ) = x3 2 x 3 y 2 .
x3 2 x y = x3 2 x 3 y 2 y = 3 y 2 .
( y ) = 3 y 2 dy = y 3.
Тогда выражение для функции
примет вид
U ( x; y )
U ( x; y ) = x3 y 2 xy 3 x y 3 ,
и общий интеграл уравнения
U ( x; y ) = C
x3 y y 3 2 xy 3x = C.
или
34.
2. (3x 2 6 xy 2 ) dx (6 x 2 y 4 y 3 ) dy = 0,y (1) = 1
Данное уравнение является уравнением в полных дифференциалах, т.к.
Py ( x; y ) = (3x 2 6 xy 2 ) y = 12 xy,
Py ( x; y ) = Qx ( x; y )
2
3
Qx ( x; y ) = (6 x y 4 y ) x = 12 xy,
Выполнение критерия означает, что существует некая функция
U ( x; y ) , для которой
U
2
2
P ( x; y ) = 3 x 6 xy = x
Q( x; y ) = 6 x 2 y 4 y 3 = U
y
35.
Из первого равенства, интегрируя поx,
находим
U1 ( x; y ) = (3x 2 6 xy 2 )dx = x3 3 x 2 y 2 ,
Из второго равенства, интегрируя по
yнаходим
,
U 2 ( x; y ) = (6 x 2 y 4 y 3 )dy = 3 x 2 y 2 y 4
Искомая функция
U ( x; y ) = U1
(недостающие слагаемые
Общий интеграл уравнения
из
U 2 ) = x3 3x 2 y 2 y 4
x3 3x 2 y 2 y 4 = c
36.
y23. x e dx x y e
Здесь
2
y2
tg 2 y dy = 0.
y2
2
P( x; y ) = x e , Q( x; y ) = x y e
y2
tg 2 y.
y2
y2
Py = 2 xye , Qx = 2 xye .
Проверяем критерий:
Частные производные равны. Данное уравнение есть уравнение
в полных дифференциалах. Нужно найти функцию
U ( x; y ).
Из
Из
U x = P ( x; y ) = x e
y2
2
U y = Q( x; y ) = x y e
U1 ( x; y ) = x e
находим
y2
tg 2 y
y2
x 2 y2
dx = e .
2
находим
2
y2
2
2 1 y2
U 2 ( x; y ) = x y e tg y dy = x e tgy y.
2
вторая функция включает в себя первую, поэтому
x 2 y2
U ( x; y ) = e tgy y.
2
Общий интеграл уравнения
x 2 y2
e tgy y = C.
2
37. Уравнения высших порядков
Дифференциальным уравнением 2 го порядка называется уравнение,которое содержит независимую переменную
и ее производные
x,
искомую функцию y,
1-го и 2-го порядка.
Уравнение 2 го порядка может быть записано в я в н о й форме
y = f ( x; y; y ),
если оно разрешено относительно старшей производной
или в н е я в н о й
F ( x; y; y ; y ) = 0.
Р е ш е н и е м дифференциального уравнения 2 го порядка
называется любая дважды дифференцируемая функция y = y ( x),
которая при подстановке в уравнение, обращает его в тождество.
38.
О б щ и м р е ш е н и е м уравнения 2-го порядка называется функцияy = y ( x; C1; C2 )
Заметим, что количество констант в общем решении уравнения
равно порядку уравнения.
З а д а ч а К о ш и для уравнения состоит в нахождении
частного решения уравнения, удовлетворяющего заданным
начальным условиям.
Н а ч а л ь н ы м и у с л о в и я м и для уравнения 2 го
порядка являются задания значений искомой функции
и ее производных при заданном значении x = x0 .
y ( x0 ) = y0 ,
y ( x0 ) = y0 .
Аналитический аппарат решения уравнений высшего порядка достаточно
хорошо разработан для линейных уравнений. Нелинейные уравнения
можно аналитически решить только, если удается понизить порядок
уравнения до первого. Но понизить порядок уравнения возможно в
следующих случаях.
39. Уравнения, допускающие понижение порядка
Тип I. Уравнения видаy ( n ) = f ( x).
Решение такого уравнения находится путем
последовательного интегрирования.
1. y (4) = sin x 2 x.
y = y (4) dx = (sin x 2 x) dx = cos x x 2 C1.
3
x
y = y dx = ( cos x x 2 C1 ) dx = sin x C1x C2 .
43
2
3
x
x
x
y = y dx = ( sin x C1x C2 ) dx =cos x C1 C2 x C3.
12
2
3
x4
x2
y = y dx = (cos x C1 C2 x C3 ) dx =
12
2
x4
x3
x2
= sin x C1 C2 C3 x C4 общее решение уравнения
60
6
2
40.
F ( x; y ; y ) = 0.Тип II.
Уравнения второго порядка, не содержащие явно искомую функцию
Уравнения этого типа сводятся к уравнениям 1-го порядка
с помощью подстановки
y = z ( x), y = ( y ) x = z ( x)
Уравнение примет вид F ( x; z ( x ); z ( x))=0,
находим сначала функцию
решая которое
z ( x, C1 ) = y x ,
а затем, интегрируя эту функцию, находим искомую функцию
y ( x; C1; C2 )
y = y x dx = z ( x; C1 ) dx C2 .
41.
2. y x ln x y = 0.Уравнение второго порядка не содержит в явном виде функцию
Делаем подстановку
y = z ( x), тогда
y
y = ( y ) x = z ( x).
После подстановки получаем уравнение первого порядка
z x ln x z = 0.
Это уравнение допускает разделение переменных
dz
dz
dx
dz
dx
x ln x = z;
=
, =
,
dx
z x ln x
z
x ln x
ln | z |= ln | ln x | ln C1, z = C1 ln x.
Интегрируя, находим искомую функцию, т.е. получаем общее решение
y = y x dx = C1 ln x dx = C1 x(ln x 1) C2 .
(Интеграл решался методом интегрирования по частям)
42.
F ( y; y ; y ) = 0.Тип III. Уравнения второго порядка вида
В уравнении отсутствует в явном виде независимая переменная
Порядок уравнения можно понизить до первого подстановкой
y x = p ( y ),
тогда
y xx = p y y x = p y p =
dp
p.
dy
3. y y e y = 0.
y
p
p
pe
=0
y y e y = 0
y x = p( y ), y x = p y p
p ( p e y ) = 0.
1) p = 0, y x = 0, y = const.
dp
2)
= e y dp = e y dy p = e y C1,
dy
dy
dy
y = e y C1
= e y C1 y
= dx.
dx
e C1
Интегрируя, получаем
1
y ln (C1 e y ) = x C2
C1
x.
43.
4. Решить задачу Кошиy =
y =
1
, y (0) = y (0) = 0.
y
1
1
dp
1
p p=
p=
y
=
p
(
y
),
y
=
p
p
dy
y
y
y
x
x
y
dy
p2
C1
p
dp
=
=
2
y
p = 4 y C1 .
y 2
2
Так как y (0) = p (0) = 0
и
y (0) = 0, то можно сразу найти C1
0 = 4 0 C1
Итак, имеем
C1 = 0.
y = 4 y 0 = 24 y
dy
dy
2
= 2 4 y
= dx 4 y 3 = x C2 .
dx
3
24 y
Так как
y (0) = 0 , то 2 4 03 = 0 C C = 0.
2
2
3
4/3
3
y
=
Частное решение x = 2 4 y 3 .
x .
или
2
3
44. Линейные уравнения 2 - го порядка
Линейным дифференциальным уравнением второго порядка называетсяуравнение, в котором искомая функция y (x ) и ее производные
входят в первых степенях и не перемножаются.
Линейное дифференциальное уравнение 2-го порядка имеет вид
ay b y c y = f ( x).
Если f (x) = 0,
то уравнение называется о д н о р о д н ы м .
Если f ( x ) 0,
то уравнение называется н е о д н о р о д н ы м .
45. Однородные линейные уравнения
Теорема о структуре общего решения линейногооднородного уравнения 2-го порядка
Если функции
y1 ( x), y2 ( x)
являются линейно независимыми
решениями линейного однородного уравнения ay b y c y
то его общее решение является их линейной комбинацией
=0
Y = C1 y1 ( x) C2 y2 ( x).
Метод решение линейного однородного уравнения с постоянными
коэффициентами – это метод Эйлера
Решение уравнения ищется в виде
y ( x) = e kx y = k e kx , y = k 2 e kx .
После подстановки в уравнение получаем квадратное уравнение
ak 2 b k c = 0,
которое называется х а р а к т е р и с т и ч е с к и м уравнением
46.
Характеристическое уравнение получается из данногодифференциального формальной заменой в нем
y k 2 , y k , y 1.
Формулы для нахождения корней квадратного уравнения
ak b k c = 0
b b 2 4ac
k1,2 =
,
2a
2
b b 2 4c
k1,2 =
,
2
2
k bk c = 0
ak 2 2b k c = 0
k 2 2b k c = 0
b b 2 ac
k1,2 =
,
a
k1,2 = b b 2 c .
47.
D = b 2 4acВ зависимости от знака дискриминанта
уравнения возможны три случая.
1. Если D 0, уравнение имеет два различных действительных корня
k1 k2
и две линейно независимых функции
y1 = e
k1x
и
k2 x
y2 = e ,
из которых составляется общее решение однородного уравнения
Y = C1 y1 C2 y2
Y = C1e
k1x
C2 e
k2 x
(1)
2. Если D 0, уравнение имеет два одинаковых действительных корня
kx
и
две
линейно
независимых
функции
и y2 = xe
y
=
e
k1 = k2 = k
1
из которых составляется общее решение однородного уравнения
Y = e kx (C1 C2 x)
(2)
3. Если D 0,уравнение имеет пару комплексно-сопряженных корней
x
k1,2 = i и две линейно независимых функции y1 = e cos x,
y2 = e x sin x и общее решение уравнения имеет вид
Y =e x (C1 cos x C2 sin x)
(3)
kx
48.
1. y 3 y 2 y = 0.y 3 y 2 y = 0 k 2 3k 2 = 0 k1,2 =
k1 = 2, k2 = 1,
3 9 8 3 1
=
,
2
2
( D > 0, k1 k2 ), Y = C1 e 2 x C2 e x .
2. 2 y 5 y 2 y = 0.
2 y 5 y 2 y = 0 2k 2 5k 2 = 0
k1,2 =
5 25 16 5 3
=
k1 = 1/2, k2 = 2,
4
4
( D > 0, k1 k2 ),
Y = C1 e x/2 C2 e 2 x .
3. y 4 y = 0.
y y = 40 k 2 4k = 0 k (k 4) = 0
4x
Y
=
C
C
e
.
k1 = 0, k 2 = 4, (k1 k 2 ),
1
2
49.
4. y 4 y 4 y = 0.y 4 y 4 y = 0 k 2 4k 4 = 0 k1,2 = 2 4 4 = 2,
или ( k 2) 2 = 0, k1 = k 2 = 2,
2 x
( D = 0), Y = e (C1 C2 x).
5. 36 y 12 y y = 0.
36 y 12 y y = 0 36k 2 12k 1 = 0 ,
или
(6k 1) 2 = 0, k1 = k 2 = 1 / 6,
( D = 0),
Y = e x / 6 (C1 C2 x).
50.
Рассмотрим случай отрицательного дискриминанта квадратногоуравнения. Оно имеет в этом случае комплексно-сопряженные корни
Числа
k1, 2 i.
и действительные, а i мнимая единица, определяемая
2
соотношением i = 1 или i = 1.
Теперь можно записывать решения
уравнений
с отрицательным дискриминантом:
квадратных
x 2 1 = 0 x 2 = 1 x1,2 = 1 = i, = 0, = 1.
x 2 4 = 0 x 2 = 4 x1,2 = 4 = 2 1 = 2i, = 0, = 2.
x 2 4 x 5 = 0 x1,2 = 2 4 5 = 2 i, = 2, = 1.
1 1 8 1 7 1 i 7 1 7 i,
x x 2 = 0 x1,2 =
=
=
= 2 2
2
2
2
2
1
7
= , =
.
2
2
51.
6. y 6 y 13 y = 0.y 6 y 13 y = 0 k 2 6k 13 = 0
k1,2 = 3 9 13 = 3 4 = 3 2 i,
( D < 0, k1,2 = i ),
= 3, = 2,
Y = e 3 x (C1 cos 2 x C2 sin 2 x).
7. y 25 y = 0.
y 25 y = 0 k 2 25 = 0 k 2 = 25 k1,2 = 5 i,
( D < 0, k1,2 = i ),
= 0, = 5,
Y = C1 cos 5 x C1 sin 5 x.
52.
8. y y y = 0.y y y = 0 k 2 k 1 = 0
k1,2 =
1 1 4 1 3 1 3i 1
3
=
=
=
i,
2
2
2
2 2
( D < 0, k1,2 = i ),
x/2
= 1/2, = 3/2,
3
3
Y = e C1 cos
x C2 sin
x .
2
2
53. Неоднородные линейные уравнения 2-го порядка с постоянными коэффициентами
Рассмотрим уравнения вида ay b y c y = f ( x ),Теорема о структуре общего
решения
неоднородного
линейного
уравнения.
Е
Y * -- какое-либо частное решение данного
сли
неоднородного уравнения, а Y общее решение
соответствующего однородного уравнения,
то общее решение Y
уравнения есть сумма
Y = Y Y .
*
неоднородного
54. Метод неопределенных коэффициентов
Этот метод позволяет находить частное решение неоднородногоуравнения в случаях, когда правая часть уравнения имеет
специальный вид f ( x) = e x P ( x) cos x Q( x) sin x ,
где P ( x), Q ( x) многочлены.
Схема нахождения общего решения
1. Записываем и решаем соответствующее однородное уравнение
ay b y c y = 0
ak 2 b k c = 0. Находим корни и
получаем общее решение однородного уравнения в виде
Y = C1 y1 ( x) C2 y2 ( x).
*
2. Находим частное решение неоднородного уравнения Y
Это частное решение должно повторять в общем виде выражение
для правой части неоднородного уравнения f (x).
55.
3. Кроме того, определяем характерное числоz = i(в общем случае - комплексное), которое нужно
сопоставить
с корнями характеристического уравнения. При этом:
а) если это число не является корнем
характеристического уравнения, то выражение для
повторяет общий вид правой части
уравнения,
б) если это число является однократным корнем
характеристического уравнения, то это выражение
необходимо умножить на x,
в) если это число является двукратным корнем
характеристического уравнения, то выражение общего вида
необходимо умножить на x 2 .
4. После подстановки в уравнение и нахождения коэффициентов
записываем выражение для Y *
и общее решение в виде
Y = Y Y *.
56.
Выражения для многочленов с неопределенными коэффициентами:A
Ax B
A x 2 Bx C
многочлен нулевой степени,
многочлен 1-ой степени,
многочлен 2-ой степени,
A x 3 Bx 2 Cx D многочлен 3-ей степени и т.д.
Выражения для случая тригонометрических функций в правой части
A cos x B sin x
( Ax B ) cos x (Cx D) sin x
( Ax 2 Bx C ) cos x ( Dx 2 Ex F ) sin x
И т.п.
57.
1. y 3 y 2 y = 3 x.y 3 y 2 y = 0 k 2 3k 2 = 0 k1 = 1, k2 = 2.
а)
Y = C1 e x C2 e 2 x общее решение однородного уравнения
б)
f ( x) = 3x
Проверяемое в этом случае число z i 0
не совпадает с корнями характеристического уравнения, поэтому
частное решение повторит в общем виде правую часть уравнения,
Y * = Ax B.
в) Общее решение:
Y = Y Y * = C1 e x C2 e 2 x ( Ax B ).
Неопределенные коэффициенты пока не нахдим.
58.
2. y 4 y = 2 x 2 1.a)
y 4 y = 0, k 2 4k = 0, k1 = 0, k2 = 4.
Y = C1 C2 e 4 x
b)
общее решение однородного уравнения
f ( x) = (2 x 2 1)
Проверяемое в этом случае число z i 0
совпадает с одним из корней характеристического уравнения,
поэтому частное решение повторит в общем виде правую часть
уравнения и дополнительно умножается на x1
Y * = ( Ax 2 Bx C ) x частное решение неоднородного уравнения
c) Общее решение:
Y =Y Y *=C1 C2 e 4 x ( Ax 2 Bx C ) x.
59.
3. y y = 3e x .a)
y y = 0, k 2 1 = 0, k1,2 = i.
Y = C1 cos x C2 sin x
b)
общее решение однородного уравнения
f ( x) = 3 e x
Проверяемое в этом случае число z i 1
не совпадает с корнями характеристического уравнения, поэтому
частное решение повторит в общем виде правую часть
уравнения
Y * = A e .
x
c) Общее решение:
Y = Y Y * = C1 cos x C2 sin x A e x .
60.
3. y 4 y = (5 x 1) e 2 x .а)
y 4 y = 0, k 2 4 = 0, k1 = 2, k2 = 2.
Y = C1 e 2 x C2 e 2 x
b)
общее решение однородного уравнения
f ( x) = (5 x 1) e 2 x
Проверяемое в этом случае число
z i 2
совпадает с одним из корней характеристического уравнения,
поэтому частное решение, повторив в общем виде правую часть
уравнения, дополнительно умножается на x
Y * = ( Ax B) e 2 x x частное решение
Общее решение неоднородного уравнения
Y = Y Y * = C1 e 2 x C2 e 2 x ( Ax B ) x e 2 x .
61.
4. y 6 y 9 y = x 2 e 3 x .y 6 y 9 y = 0, k 2 6k 9 = 0, k1 = k2 = 3.
а)
Y = (C1 C2 x) e 3 x
б)
общее решение однородного уравнения
f ( x) = x 2 e 3 x
Проверяемое в этом случае число
= 3
совпадает с обоими корнями характеристического уравнения,
поэтому частное решение, повторив в общем виде правую часть
уравнения, дополнительно умножается на x 2
Y * = ( Ax 2 Bx C ) e 3 x x 2 .
Общее решение неоднородного уравнения
Y = Y Y * = (C1 C2 x) e 3 x ( Ax 2 Bx C ) e 3 x x 2 .
62.
5. y 2 y = 3 cos 2 x.a)
y 2 y = 0, k 2 2k = 0, k1 = 0, k2 = 2.
Y = C1 C2 e 2 x
b)
общее решение однородного уравнения
f ( x) = 3 cos 2 x
Проверяемое в этом случае число i = 2i не совпадает с корнями
характеристического уравнения, поэтому частное решение
повторит в общем виде правую часть уравнения, т.е.
Y * = A cos 2 x B sin 2 x.
c) Записываем общее решение неоднородного уравнения
Y = Y Y * = C1 C2 e 2 x A cos 2 x B sin 2 x.
63.
6. y 16 y = 2 sin 4 x.a)
y 16 y = 0, k 2 16 = 0, k1 = 4i.
Y = C1 cos 4 x C2 sin 4 x общее решение однородного уравнения
b)
f ( x) = x sin x
Проверяемое в этом случае число
i = 4i совпадает с корнями
характеристического уравнения, поэтому частное решение
поэтому частное решение, повторив в общем виде правую часть
уравнения, дополнительно умножается на x
Y * = ( A cos 4 x B sin 4 x) x.
c) Записываем общее решение неоднородного уравнения
Y = Y Y * = C1 cos 4 x C2 sin 4 x ( A cos 4 x B sin 4 x) x.
64.
7. y y 2 y = x sin x.a)
y y 2 y = 0, k 2 k 2 = 0, k1 = 1, k2 = 2.
Y = C1 e x C2 e 2 x
b)
общее решение однородного уравнения
f ( x) = x sin x
Проверяемое в этом случае число i = 1 i не совпадает с корнями
характеристического уравнения, поэтому частное
решение
повторит в общем виде правую часть уравнения, т.е.
Y * = ( Ax B ) cos x (Cx D ) sin x.
с)
Записываем общее решение неоднородного уравнения
Y = Y Y * = C1 e x C2 e 2 x ( Ax B ) cos x (Cx D) sin x.
65.
3x8. y 4 y = e cos 2 x.
y 4 y = 0, k 2 4 = 0, k1,2 = 2i.
Y = C1 cos 2 x C2 sin 2 x
общее решение однородного уравнения
f ( x) = e3 x cos 2 x
i = 3 2 i уравнения,
Проверяемое
в этом
число
не совпадает
с случае
корнями
характеристического
поэтому
частное решение повторит в общем виде правую часть
уравнения,
Y * = e 3 x ( A cos 2 x B sin 2 x).
Записываем общее решение неоднородного уравнения
Y = Y Y * = C1 cos 2 x C2 sin 2 x e 3 x ( A cos 2 x B sin 2 x).
66.
2 x9. y 4 y 5 y = e sin x.
y 4 y 5 y = 0, k 2 4k 5 = 0, k1,2 = 2 i.
Y = e 2 x (C1 cos x C2 sin x) общее решение однородного уравнения
f ( x) = e 2 x sin x
Проверяемое в этом случае число
i = 2 i
совпадает с корнями характеристического уравнения, поэтому
частное решение повторит в общем виде правую часть уравнения
и дополнительно умножается на x
Y * = e 2 x ( A cos x B sin x) x.
Записываем общее решение неоднородного уравнения
Y = Y Y * = e 2 x (C1 cos x C2 sin x) e 2 x ( A cos x B sin x) x.
67.
Рассмотрим примеры, в которых показаны приемы нахождениянеопределенных коэффициентов
1. y 4 y 4 y = 5 x 3.
y 4 y 4 y = 0, k 2 4k 4 = 0,
2
(k 2) = 0, k1 = k2 = 2 Y = (C1 C2 x)e
2 x
f ( x) = 5 x 3.
Проверяемое в этом случае число "0" не совпадает ни с одним
корнем характеристического уравнения, поэтому частное
решение повторит в общем виде правую часть уравнения, т.е.
Y * = Ax B.
Для нахождения пока неопределенных коэффициентов
подставим это решение в исходное уравнение вместо y ,
найдя предварительно (Y * ) = A, (Y * ) = 0.
A, B
.
68.
Тогдаy 4 y 4 y = 5 x 3, 4 A 4( Ax B) = 5 x 3,
4 Ax (4 A 4 B) = 5 x 3.
Приравнивая коэффициенты при одинаковых степенях
в левой и правой частях равенства, имеем
x1 : 4 A = 5,
x : 4 A 4B = 3
0
A = 5/4,
B = 1/2.
Записываем частное решение
c)
Общее
уравнения:
5x 1
Y* =
.
4 2
решение
неоднородного
Y = Y Y = (C1 C2 x)e
*
2 x
5x 1
.
4 2
x
69.
2. y 3 y = x 2 x.y 3 y = 0, k 2 3k = 0, Y = C1 C2e3 x .
Правая часть уравнения есть многочлен 2-ой степени и проверяемое
число z = 0 cовпадает с одним из корней характеристического
уравнения, поэтому выражение для Y *
повторит общий вид правой части и будет содержать множитель x
Y * = x ( Ax 2 B x C ) = A x 3 B x 2 C x.
Подставим это
предварительно
выражение
(Y * ) = 3 Ax 2 2 Bx C ,
Имеем
многочленов
равенство
в
исходное
уравнение,
(Y * ) = 6 Ax 2 B.
двух
6 Ax 2 B 3(3 Ax 2 2 Bx C ) = x 2 x.
Приравниваем коэффициенты при одинаковых степенях
в левой и правой частях
равенства
x
найдя
70.
6 Ax 2 B 3(3 Ax 2 2 Bx C ) = x 2 x.1
x2 : 9 A = 1 A = ,
9
1
x1 : 6 A 6 B = 1 B = ,
18
1
x 0 : 2 B 3C = 0 C = .
27
Частное решение
Общее
уравнения
1
1 2
1
Y = x x x .
9
27 18
*
решение
неоднородного
1
1 2
1
Y = Y Y = C1 C2 e x x x .
9
27 18
*
3x
71.
3. y 2 y y = (2 x 3) e x .2
y 2 y y = 0, k 2 2k 1 = 0, (k 1) = 0, k1 = k2 = 1.
Y = (C1 C2 x) e x
общее решение однородного уравнения
Находим частное решение Y *
Правая часть f ( x) = (2 x 3) e x и число
z = =1
двукратным корнем характеристического уравнения, поэтому
выражение для Y * повторит общий вид правой части и
будет содержать множитель x 2
Y * = x 2 ( Ax B) e x = ( Ax3 Bx 2 ) e x .
Подставим это
предварительно
выражение
в
исходное
уравнение,
найдя
72.
y 2 y y = (2 x 3) e x .(Y * ) = ( Ax3 (3 A B ) x 2 2 Bx) e x ,
(Y * ) = ( Ax3 (6 A B) x 2 (6 A 4 B) x 2 B ) e x .
*
*
*
x
Подставим Y , (Y ) , (Y ) в уравнение и сократим на e
[ Ax 3 (6 A B ) x 2 (6 A 4 B) x 2 B]
2[ Ax 3 (3 A B ) x 2 2 Bx] [ Ax 3 Bx 2 ] = (2 x 3),
раскрываем скобки и приводим подобные
1
Откуда имеем
6 Ax 2 B = 2 x 3.
3
6 A = 2, A = , 2 B = 3, B = .
3
2
Записываем частное решение
Общее
уравнения
решение
3
1
Y * = x 2 e x x .
2
3
неоднородного
3 1
Y = (C1 C2 x) e x x 2 e x x .
2 3
73.
Y*
=
A cos 4 x
B sin 4 x.
4. y 4 y 20 y = 4 cos 4 x 52 sin 4 x.
y 4 y 20 y = 0, k 2 4k 20 = 0,
k1,2 = 2 4 20 = 2 4i,
Y = e 2 x (C1 cos 4 x C2 sin 4 x).
Y*
Правая часть f ( x ) = 4 cos 4 x 52 sin 4 x.
Составляем выражение для
Проверяемое число
z = i = 4i
не является корнем характеристического уравнения, поэтому
выражение для Y * просто повторит общий вид правой части
Y * = A cos 4 x B sin 4 x.
Для нахождения неопределенных коэффициентов найдём первую и
вторую производные от Y *
*
(Y ) = 4 A sin 4 x 4 B cos 4 x,
(Y * ) = 16 A cos 4 x 16 B sin 4 x.
74.
Подставимуравнение
их
в
исходное
16 A cos 4 x 16 B sin 4 x 4( 4 A sin 4 x 4 B cos 4 x) 20( A cos 4 x B sin 4 x) =
4 cos 4 x 52 sin 4 x.
Приведем подобные члены:
(4 A 16 B ) cos 4 x ( 16 A 4 B ) sin 4 x = 4 cos 4 x 52 sin 4 x.
Приравнивая в этом равенстве коэффициенты
при синусах и косинусах имеем систему
уравнений
sin 4 x : 16 A 4 B = 52
A = 3,
cos 4 x : 4 A 16 B = 4
B = 1.
Частное решение:
Y * = 3 cos 4 x sin 4 x.
Общее решение исходного уравнения
Y = Y Y * = e 2 x (C1 cos 4 x C2 sin 4 x) 3 cos 4 x sin 4 x.
75. Консультация к вебинару 14
76. Системы дифференциальных уравнений
Системой линейных дифференциальных уравнений с постояннымикоэффициентами называются системы вида
dx
dt = a1 x b1 y f1 (t ),
1)
неоднородная система
dy
= a2 x b2 y c2 z f 2 (t )
dt
dx
dt = a1 x b1 y,
однородная система
dy
2) = a2 x b2 y,
dt
Решение
системы - это совокупность функций, обращающих каждое
уравнение системы в тождество
x(t )
X (t ) =
y (t )
77. Метод исключения решения систем
Этот метод представляет собой метод сведения системы кодному
уравнению высшего порядка. Метод достаточно прост и легко
реализуем
для системы
2-го порядка.
Найти общее
решение
однородной
системы
dx
dt = 2 x y,
dy
= 8 x 4 y.
dt
d 2x
dx dy
=2 .
2
dt
dt dt
a) Продифференцируем первое уравнение по t
2
d
подставим из второго уравнения x = 2 dx 8 x 4 y,
b) Значение y
dt 2
dt
dx
c) Значение y находим из первого уравнения
y
=
2x
2
dt
и подставляем d x = 2 dx 8 x 4( dx 2 x ),
dt 2
dt
dt
d 2x
dx
6 = 0.
Окончательно система свелась к уравнению
2
dt
dt
78.
Находим его общее решениеd 2x
dx
2
6
=
0,
k
6k = 0, k1 = 0, k 2 = 6.
2
dt
dt
x(t ) = C1 C2e6t .
Вторую функцию
y=
y (t ) находим согласно 1-му уравнению системы
dx
2 x = (C1 C2 e 6t ) 2(C1 C2 e 6t ) = 6C2 e 6t 2C1 2C2 e 6t
dt
y (t ) = 2C1 4C2e6t .
Общее решение системы
x(t ) = C1 C2e6t
6t
y
(
t
)
=
2
C
4
C
e
1
2
79.
Найтисистемы
общее
решение
неоднородной
dx
dt = 4 y 6 cos t ,
dy
= x.
dt
a) Продифференцируем первое уравнение по t
d 2x
dy
=
4
6 sin t.
2
dt
dt
dy
b) Значение
подставим из второго уравнения
dt
d 2x
= 4 x 6 sin t.
2
dt
Таким образом, имеем неоднородное уравнение
d 2x
4 x = 6 sin t.
2
dt
Решаем сначала соответствующее однородное уравнение
80.
d 2x4x = 0
2
dt
k 2 4 = 0, k1,2 = 2i :
x(t ) = C1 cos 2t C2 sin 2t.
Частное решение уравнения ищем по виду правой части
x* = A cos t B sin t.
( x* ) ' = A s int B cos t ,
( x* ) '' = A cos t B sin t ,
После подстановки в уравнение и нахождения неопределенных
коэффициентов имеем
A cos t B sin t 4( A cos t B sin t ) 6 sin t ,
3 A cos t 3B sin t 6 sin t ,
Частное решение
x* = 2 sin t.
A 0, B 2,
81.
Общее решение для первой функцииx(t ) = C1 cos 2t C2 sin 2t 2 sin t.
Находим вторую функцию.
Из первого уравнения системы
имеем
1 dx
1
y = ( 6 cos t ) = (2C1 sin 2t 2C2 cos 2t 2 cos t 6 cos t )
4 dt
4
1
= (C1 sin 2t C2 cos 2t cos t 3 cos t ).
2
Ответ:
x(t ) = C1 cos 2t C2 sin 2t 2 sin t ,
y (t ) = 1 (C sin 2t C cos 2t cos t 3 cos t ).
1
2
2










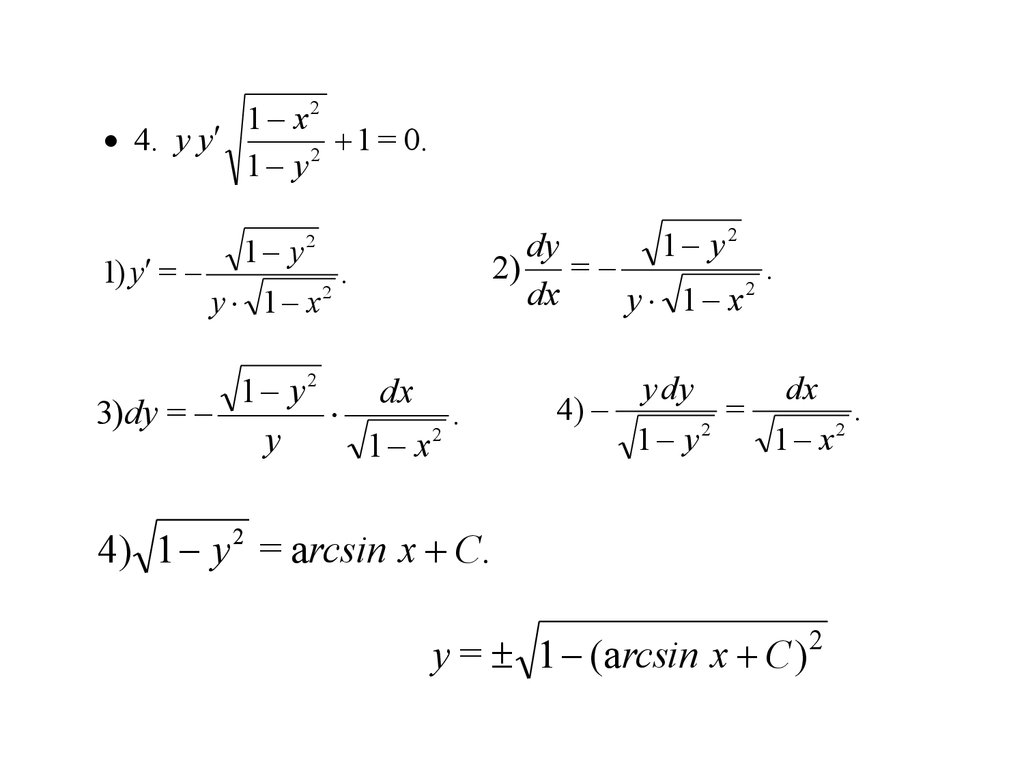





















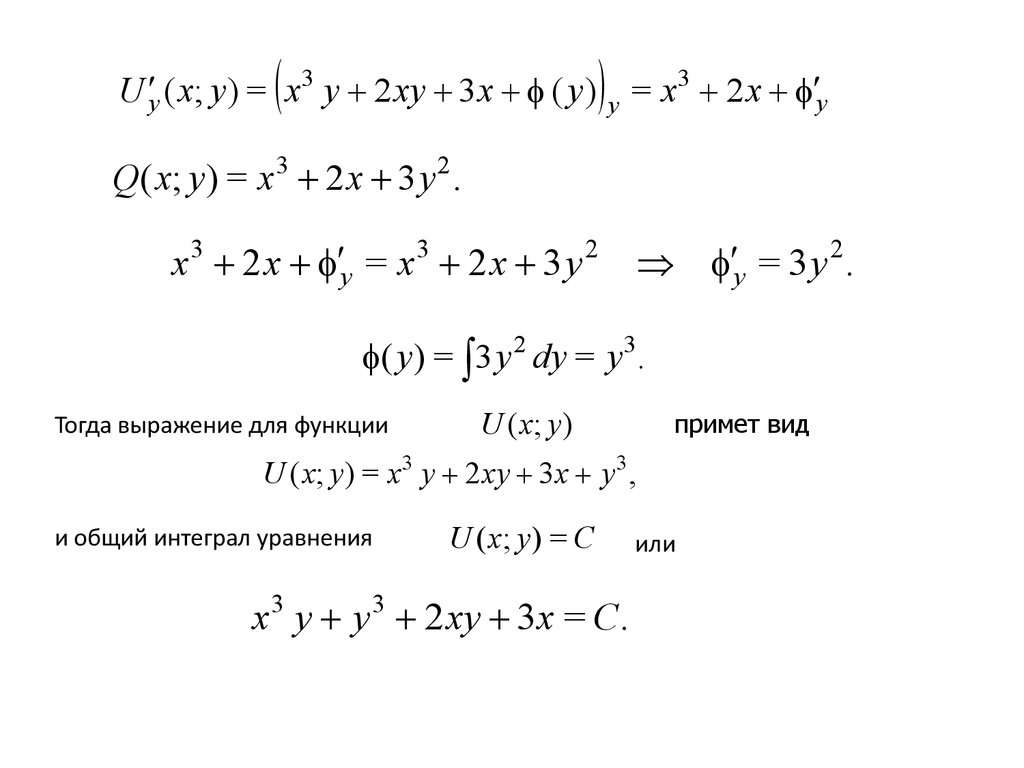















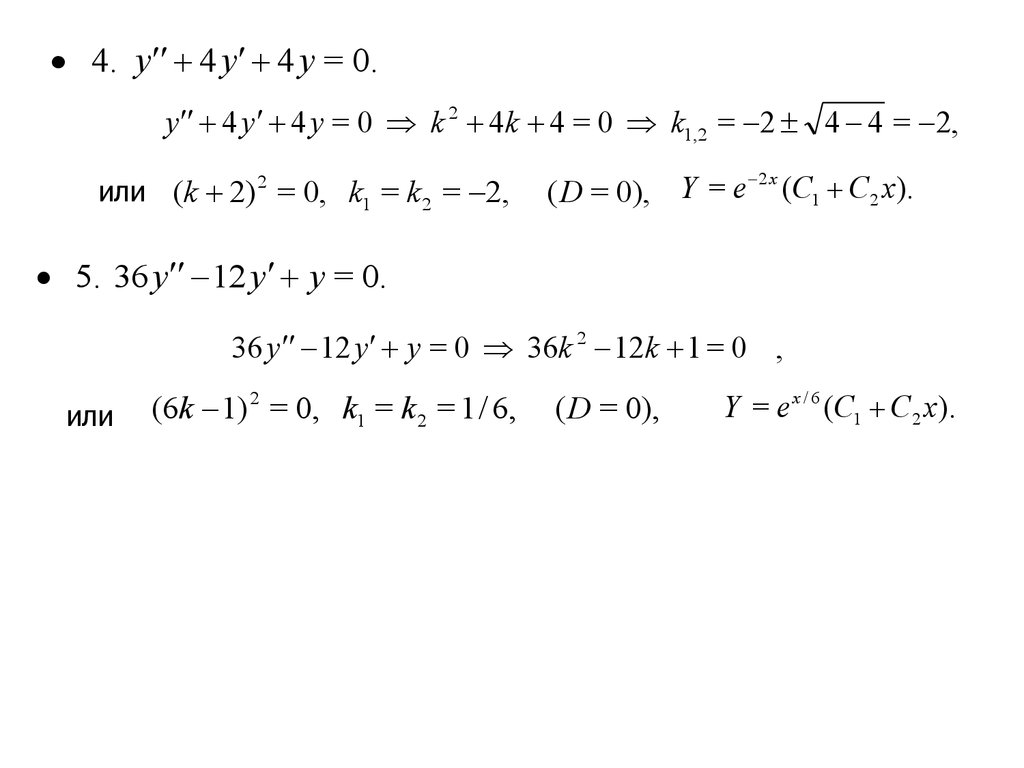


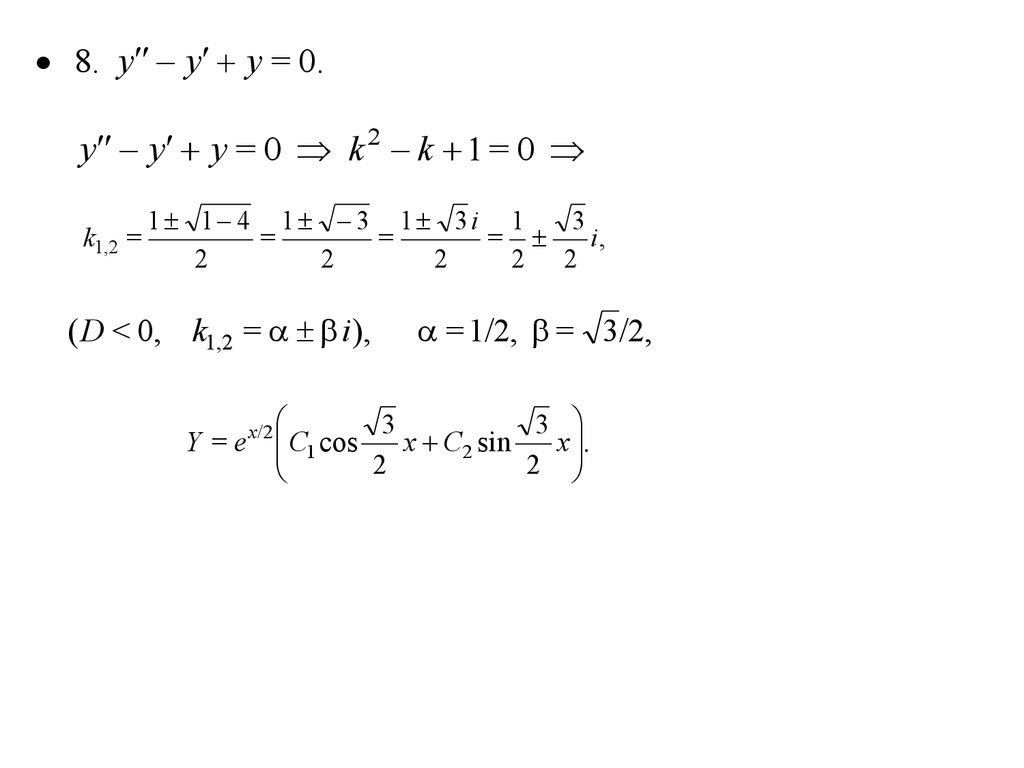






























 mathematics
mathematics








