Similar presentations:
Интегральное исчисление. Дифференциальные уравнения
1. Интегральное исчисление. Дифференциальные уравнения
2. Элементы интегрального исчисления
1.Первообразная и неопределенныйинтеграл
2.Основные приемы вычисления
неопределенных интегралов
3.Интегрирование функций, содержащих
квадратный трехчлен
4.Интегрирование дробно-рациональных
функций
5.Интегрирование тригонометрических
функций
6.Интегрирование некоторых
иррациональностей
3. Первообразная и неопределенный интеграл
Если F x - первообразная функции f x ,то F x C , где C - некоторая постоянная,
также является первообразной функции
f x .
Если F x есть какая-либо первообразная
функции f x , то всякая функция вида
Ф x F x C также является
первообразной функции f x и всякая
первообразная представима в таком виде.
4. Первообразная и неопределенный интеграл
Определение.Совокупность
всех
первообразных
функции
f x ,
определенных
на
некотором
промежутке,
называется
неопределенным
интегралом
от
функции f x на этом промежутке и
обозначается f x dx .
5. Неопределенный интеграл
Определение 1.Функция F (x ) называется первообразной для f (x) в
если F (x ) определена в ( a, b) и F ( x) f ( x)
Пример.
f ( x) sin x F ( x) cos x
( так как ( cos x) sin x )
(a, b),
6. Неопределенный интеграл
Теорема (о разности первообразных).
F ( x) и G( x) первообразные
для f ( x) в (a, b)
F ( x) G( x) const
Доказательство.
Обозначим через ( x) F ( x) G( x) .
Пусть x1 , x2 ( a, b ) .
Функция (x ) удовлетворяет
условиям теоремы Лагранжа:
а) ( x) непрерывна на x1 , x2
б) ( x) F ( x) G ( x)
f ( x) f ( x) 0 в ( x1 , x2 )
( x2 ) ( x1 ) (c)(x2 x1 ) 0
( x2 ) ( x1 ) x1 , x2 (a, b)
( x) const .
7. Неопределенный интеграл
Следствие.
Пусть F (x ) первообразная для f (x) в (
Тогда любая другая первообразная
Определение 2.
Неопределенным интегралом от f (x)
называется совокупность всех первообразных
G ( x ) F ( x) C
a , b. ) .
f ( x)dx F ( x) C
Графическая иллюстрация
y
Пример.
y F (x)
sin xdx cos x C
a
b
x
8. Свойства интеграла, вытекающие из определения
Производная неопределенногоинтеграла равна подынтегральной
функции, а его дифференциалподынтегральному выражению.
Действительно:
1.( f ( x)dx) ( F ( x) C ) F ( x) f ( x);
2.d f ( x)dx ( f ( x)dx) dx f ( x)dx.
9. Свойства интеграла, вытекающие из определения
Неопределенный интеграл отдифференциала непрерывно
дифференцируемой функции равен
самой этой функции с точностью до
постоянной:
3. d ( x) ( x)dx ( x) C ,
так как (x )
является первообразной
для (x).
10. Свойства интеграла
Сформулируем далее следующие свойстванеопределенного интеграла:
4.Если функции f1 x и f 2 x имеют
первообразные, то функция f1 x f 2 x
также имеет первообразную, причем
f1 x f 2 x dx f1 x dx f 2 x dx ;
5. Kf x dx K f x dx ;
6. f x dx f x C ;
7. f x x dx F x C .
11. Таблица неопределенных интегралов
1. dx x C .a 1
x
2. x a dx
C, (a 1) .
a 1
dx
3. ln x C .
x
x
a
4. a x dx
C .
ln a
5. e x dx e x C .
6. sin xdx cos x C .
7. cos xdx sin x C .
dx
8. 2 ctgx C .
sin x
dx
9. 2 tgx C .
cos x
dx
arctgx C .
10.
2
1 x
12. Таблица неопределенных интегралов
11.dx
arcsin x C .
1 x 2
dx
1
x
12. 2 2 arctg C .
a
a
a x
13.
a x
2
arcsin
2
x
C ..
a
x2 a
ln x x 2 a C .
17. shxdx chx C .
18. chxdx shx C .
dx
1
x a
ln
C
2
2
2a x a
x a
19.
dx
1
a x
ln
a 2 x 2 2a a x C .
20.
14.
15.
dx
dx
16.
dx
ch 2 x thx C .
dx
cthx C .
2
sh x
13. Интегрирование по частям
Этот метод основан на формуле udv uv vdu .Методом интегрирования по частям берут такие интегралы:
а) x n sin xdx , где n 1,2...k ;
б) x n e x dx , где n 1,2...k ;
в) x n arctgxdx , где n 0, 1, 2,... k . ;
г) x n ln xdx , где n 0, 1, 2,... k .
При вычислении интегралов а) и б) вводят
n 1
обозначения: x n u , тогда du nx dx , а, например
sin xdx dv ,тогда v cos x .
При вычислении интегралов в), г) обозначают за u функцию
arctgx , ln x , а за dv берут x n dx .
14. Метод замены переменной
Пусть требуется найти f x dx , причемнепосредственно подобрать первообразную
для f x мы не можем, но нам известно, что
она существует. Часто удается найти
первообразную, введя новую переменную,
по формуле
f x dx f t t dt , где x t , а t - новая
переменная
15. Задача о вычислении площади плоской фигуры
Решим задачу о вычислении площадифигуры, ограниченной графиком
функции y f x, отрезками прямых
x a, x b и осью Ox.Такую фигуру
называют криволинейной трапецией
a
xi 1 xi
b
16. Задача о вычислении площади плоской фигуры
Разобьем отрезок a, b на n частейточками a x0 , x1, x2 ,..., xi 1, xi ,..., xn b .
При этом криволинейная трапеция разобьется
на n элементарных криволинейных
трапеций. Заменим каждую такую
криволинейную трапецию прямоугольником с
основанием xi xi xi 1 , где i 1,2,.., n и
высотой h f xi , где xi -произвольно
выбранная внутри отрезка xi 1, xi точка.
17. Задача о вычислении площади плоской фигуры
Площадь прямоугольника будетравна Si f xi xi , а площадь
всей криволинейной фигуры
приблизительно будет равна
сумме площадей всех
прямоугольников:
n
n
i 1
i 1
S Si f xi xi .
18. Определенный интеграл
Определение.n
Выражение f xi xi , где
i 1
xi xi xi 1 , называется
интегральной суммой функции f x
на отрезке a, b .
19. Определенный интеграл
Определение.Если существует конечный
n
lim
f xi xi , не
max xi 0 i 1
зависящий ни от способа разбиения отрезка
a, b на части, ни от выбора точек xi xi 1 , xi ,
то этот предел называется определенным
интегралом функции f x на отрезке a, b и
b
обозначается f x dx .
a
20. Определенный интеграл
Замечание.С геометрической точки зрения
b
при f x 0 f x dx равен
a
площади криволинейной
трапеции
21. Теорема о существовании определенного интеграла
Теорема.Если функция f x непрерывна на
отрезке a, b , то
n
f xi xi
lim
max xi 0 i 1
существует и конечен, т.е.
b
существует и конечен f x dx .
a
22. Свойства определенного интеграла
a1. f x dx 0 ;
a
b
2. dx b a ;
a
b
a
3. f x dx f x dx ;
a
b
b
4. f1 x f 2 x dx f1 x dx f 2 x dx ;
a
b
b
a
a
23. Свойства определенного интеграла
bb
a
b
a
5. Kf x dx K f x dx ;
c
b
a
c
6. f x dx f x dx f x dx ;
a
b
7. f x dx 0 , если f x 0 .
a
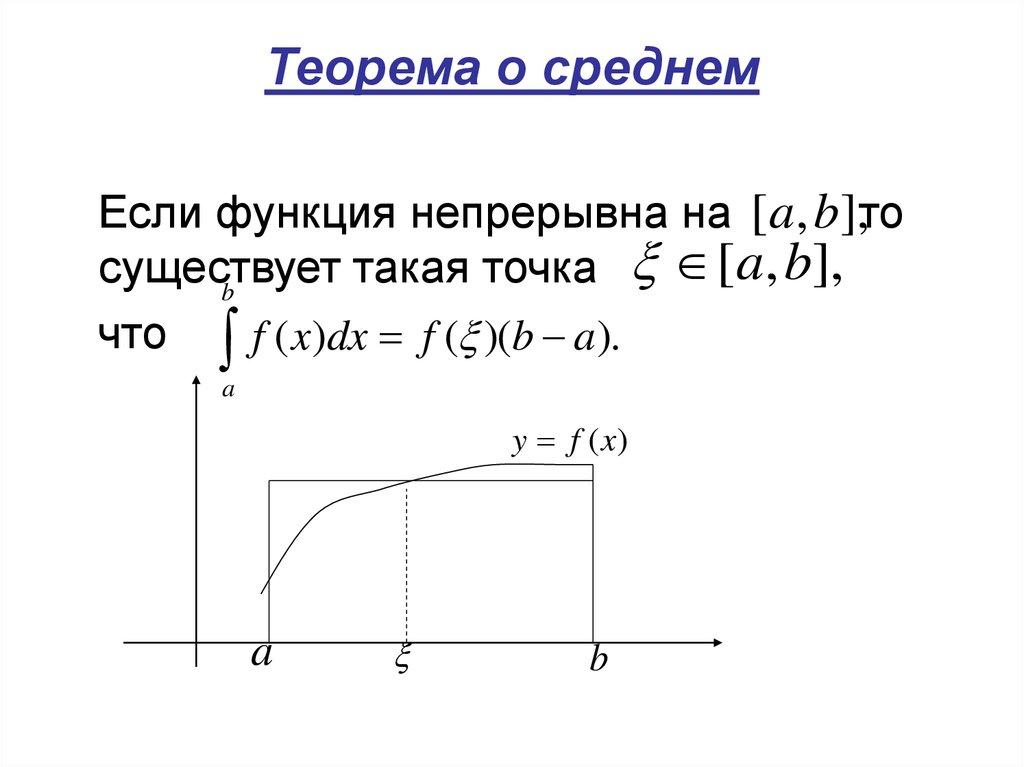
24. Теорема о среднем
Если функция непрерывна на [ a, b],тосуществует
такая точка [a, b],
b
что f ( x)dx f ( )(b a).
a
y f (x)
a
b
25. Вычисление определенного интеграла
Теорема.Пусть F x - первообразная функции f x .
b
Тогда f x dx F b F a .
a
Эту формулу называют формулой
Ньютона-Лейбница, из которой следует,
что для вычисления определенного
интеграла необходимо найти
первообразную подынтегральной функции.
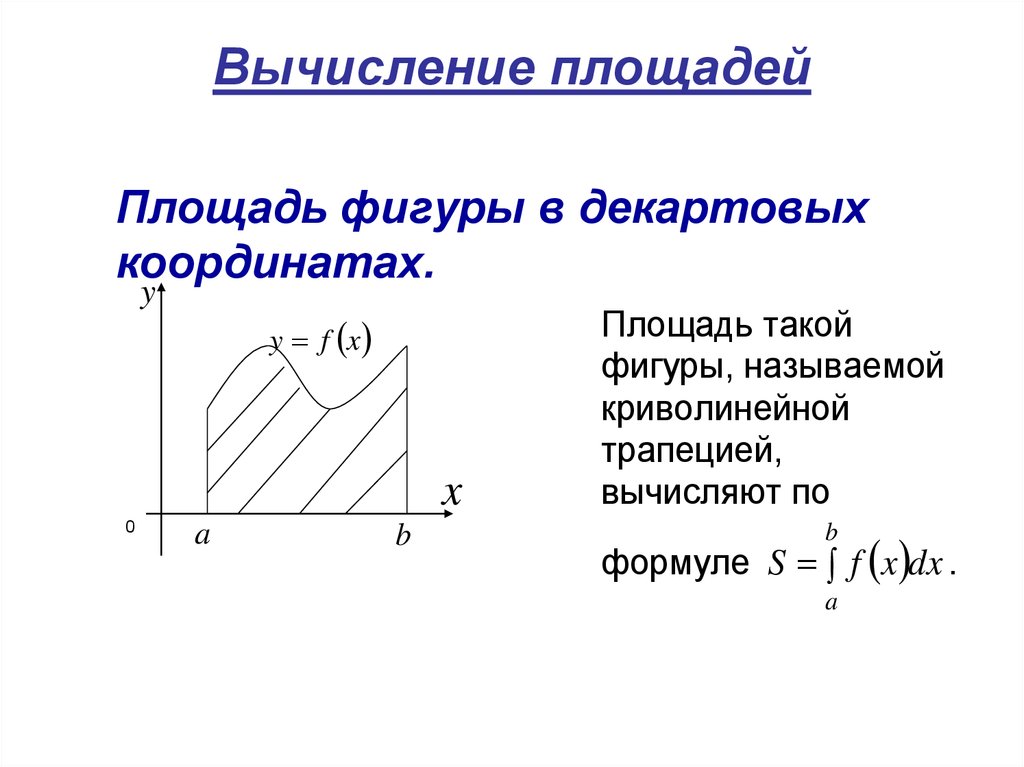
26. Вычисление площадей
Площадь фигуры в декартовыхкоординатах.
y
y f x
x
0
a
b
Площадь такой
фигуры, называемой
криволинейной
трапецией,
вычисляют по
b
формуле S f x dx .
a
27. Обыкновенные дифференциальные уравнения
28. Уравнение первого порядка
Функциональное уравнениеF(x,y,y ) = 0 или y = f(x,y), связывающее
между собой независимую
переменную, искомую функцию y(x) и
ее производную y (x), называется
дифференциальным уравнением
первого порядка.
29. Общее решение дифференциального уравнения 1-го порядка
Общим решением дифференциальногоуравнения первого порядка называется
такая функция y = (x,C), которая при
любом значении параметра C является
решением этого дифференциального
уравнения.
30.
Уравнение Ф(x,y,C) =0, определяющееобщее решение как неявную функцию,
называется общим интегралом
дифференциального уравнения первого
порядка.
31. Постановка задачи Коши
Задача отыскания решениядифференциального уравнения
,
y f ( x, y )
удовлетворяющего начальному условию
y y0 при x x0 , называется
задачей Коши для уравнения 1-го
порядка.
32. Уравнение с разделяющимися переменными
Дифференциальное уравнениеf ( x)dx g ( y )dy
называется уравнением с
разделенными переменными.
33. Уравнение с разделяющимися переменными
Дифференциальное уравнение 1-го порядканазывается уравнением с разделяющимися
переменными, если оно имеет вид:
M1 ( x ) N1 ( y )dx M 2 ( x ) N 2 ( y )dy 0
.
Для решения уравнения делят обе его части
на произведение функций
N1 ( y)M 2 ( x)
,
а затем интегрируют.
34. Однородные уравнения
Дифференциальное уравнение первогопорядка называется однородным, если
y
его можно привести к виду y = f ( )
x
или к виду M ( x , y )dx N ( x , y )dy 0
где M ( x, y ) и N ( x , y ) – однородные
функции одного порядка .
35. Линейные уравнения 1-го порядка
Дифференциальное уравнение первогопорядка называется линейным, если оно
содержит y и y в первой степени, т.е.
имеет вид
y P( x ) y Q( x ) .
Решают такое уравнение с помощью
подстановки y=uv, где u и vвспомогательные неизвестные функции,
которые находят, подставляя в уравнение
вспомогательные функции и на одну из
функций налагают определенные условия.
36. Уравнение Бернулли
Уравнением Бернулли называетсяуравнение 1-го порядка, имеющее вид
m
y P( x ) y Q( x ) y,
где m 0 и m 1
Его, как и линейное уравнение решают
с помощью подстановки
y uv
37. Основные понятия
Уравнение 2-го порядка имеет видF(x,y,y ,y ) 0
Или
y f ( x, y , y )
Общим решением уравнения второго порядка
называется такая функция y ( x , c1 , c2 ) ,
которая при любых значениях параметров c1 ,c2
является решением этого уравнения.
38. Задача Коши для уравнения 2-го порядка
Задача Коши для уравнения 2го порядкаЕсли уравнение 2-го порядка разрешить
относительно второй производной, то для
такого уравнения имеет место задача: найти
решение уравнения y f ( x, y, y ) ,
удовлетворяющее начальным условиям:
y( x0 ) y0 и y ( x0 ) y 0
Эту задачу называют задачей Коши для
дифференциального уравнения 2-гопорядка.
39. Теорема существования и единственности решения уравнения 2-го порядка
Если в уравнении y f ( x, y, y )функция f ( x, y, y ) и ее частные
производные по аргументам y и y
непрерывны в некоторой области,
содержащей точку ( x0 , y 0 , y 0 ) ,
то существует и притом единственное
решение y y (x ) этого уравнения,
удовлетворяющее условиям
y( x0 ) y0 и y ( x0 ) .y0
40. Уравнения 2-го порядка, допускающие понижение порядка
Уравнения 2-го порядка,допускающие понижение
Простейшее уравнение
2-го порядка
порядка
y f ( x ) решают двукратным
интегрированием.
Уравнение F ( x , y , y ) 0, не
содержащее явно у, решают с помощью
подстановки y p , y p
Уравнение F ( y, y , y ) 0, не
содержащее х, решают заменой
dp
y p ,
y . p
dy
41. Линейные однородные уравнения
Линейным однороднымдифференциальным уравнением
второго порядка называется уравнение
. y p( x ) y q( x ) y 0
Если все коэффициенты этого
уравнения постоянны, то уравнение
называется уравнением с постоянными
коэффициентами .
42. Линейное однородное уравнение 2-го порядка с постоянными коэффициентами
Уравнение k pk q 0 называетсяхарактеристическим уравнением
линейного уравнения y py qy 0 .
Оно получается из ЛОУ заменой
соотстветствующей порядку
производной степенью k
.
2
43. Вывод формул общего решения ЛОУ 2-го порядка
Корни характеристического уравненияk1, 2
p
2
p2
q
4
p2
Случай 1. Если
, то
q 0
4
характеристическое уравнение имеет два
различных действительных корня k1 k 2 R
В этом случае общее решение имеет вид
k1 x
k2 x
y C1e C 2 e .
44.
p2q 0
4
Случай 2. Если
, то
характеристическое уравнение имеет
одинаковые корни k1 k 2 k
.
Частные решения ЛОУ выбираем так,
чтобы они были линейно независимыми:
kx
kx
y1 e
y 2 xe .
и
Общее решение ЛОУ 2-го порядка будет
kx
y
e
(C1 xC2 ) .
иметь вид
45.
2p
q 0
Случай 3. Если
4
, то
характеристическое уравнение имеет два
комплексно-сопряженных корня
p
k1 i и k 2 i , где
2
2
p
и q
.
4
Общее решение ЛОУ 2-го порядка в
действительной форме можно записать
в виде y e x (C cos x C sin x)
1
2












































 mathematics
mathematics








