Элементы интегрального исчисления

1. Тема 3. Элементы интегрального исчисления

3.1. Первообразная. Неопределенный
интеграл. Основные понятия
3.2. Основные методы интегрирования
3.3. Задача о площади. Определенный
интеграл –основные понятия
3.4. Вычисление определенного интеграла.
Основные свойства
3.5. Несобственные интегралы
Майер И.И.
1

2.

• 3.1. Первообразная. Неопределенный
интеграл.
• Основные понятия
• Определения
Майер И.И.
2

3. Первообразная. Неопределенный интеграл.

Пусть задана дифференцируемая функция F(x).
Определим ее первую производную, функцию f(x), и
дифференциал dF. Получим
dF (1)
f ( x ) F ( x )
dx
dF ( x ) f ( x )dx
(2)
В данной задаче F(x) задана, а f(x) - результат
дифференцирования.
Рассмотрим обратную задачу: Дана функция f(x),
производная от F(x).
Требуется определить функцию F(x), первообразную
функции f(x).
Определение. Первообразной заданной функции f(x)
называется функция F(x), производная которой равна f(x)
F ( x ) f ( x )
а дифференциал dF равен :
dF ( x ) f ( x )dx
Майер И.И.
3

4. Первообразная. Неопределенный интеграл.

Пример. Пусть задана функция F(x)=x3.
Очевидно, она является первообразной функции f(x)=3x2 ,т. к.
f ( x ) F ( x ) x
3
3x
2
Но функция z=x3+5 также будет первообразной для f(x)=3x2 ,
3
2
т.к.
z ( x 5) 3x
Очевидно, что любая функция F(x) = x3+c, где c –
произвольная постоянная, имеет производную 3x2 и
поэтому будет первообразной для f(x)=3x2 .
Очевидно, задача нахождения первообразных неоднозначна
Майер И.И.
4

5.

Первообразная. Неопределенный интеграл (продолжение)
Справедливо утверждение:
Если функция F(x) - первообразная функции f(x) на интервале
(a,b), то всякая другая первообразная функции f(x) отличается
от F(x) на постоянное слагаемое c . представляется в виде
F(x)+c ,
Выражение F(x)+c представляет собой общий вид
первообразных для f(x), совокупность всех
первообразных, семейство первообразных.
Совокупность всех первообразных называется
неопределенным интегралом функции f(x) и
обозначается
f ( x )dx F ( x ) c
Операцию вычисления неопределенного интеграла называют
интегрированием функции.
Майер И.И.
5

6.

Так как
( F ( x) c) f ( x)
то
f ( x)dx f ( x).
Следовательно, если функцию f(x) проинтегрировать, а
затем полученный результат продифференцировать, то
получим снова функцию f(x).
Дифференцирование и интегрирование являются
взаимно обратными операциями.
Свойства неопределенного интеграла.
1. Неопределенный интеграл от алгебраической суммы
конечного числа функций равен алгебраической сумме
неопределенных интегралов этих функций
f ( x) q( x) h( x) dx f ( x)dx q( x)dx h( x)dx.
2. Постоянный множитель можно выносить за знак интеграла
c f ( x)dx c f ( x)dx.
Майер И.И.
6

7.

• 3.2. Основные методы интегрирования
• Таблица интегралов
• Методы вычисления неопределенных
интегралов
Майер И.И.
7

8. Основные методы интегрирования

Вычисление неопределенного интеграла - задача значительно более
сложная, чем отыскание производной.
Нет никаких общих правил для нахождения неопределенных
интегралов от произведений или частного двух функций. Нет
общего правила интегрирования сложной функции.
Кроме того, интегралы от некоторых элементарных функций,
например, интегралы от функций
exp( x ),
3
sin x
,
x
1
ln x
не являются элементарными, не берутся в элементарных
функциях.
Для вычисления неопределенных интегралов используют:
- табличные интегралы;
- преобразования подынтегрального выражения
- различные методы интегрирования
Майер И.И.
8

9.

1.
Таблица основных интегралов, с - константа
с - константа
dx x c , c
x 1
x dx
c, 1
• 2.
1
dx
ln x c
• 3.
x
x
a
x
c
• 4. a dx
ln a
• 5.
x
x
e
dx
e
c
• 6.
cos xdx sin x c
• 7.
sin xdx cos x c
Майер И.И.
9

10.

• 8.
dx
cos 2 x tgx c
• 9.
dx
sin2 x ctgx c
• 10.
dx
1
a2 x2 a arctgx c
• 11.
• 12.
dx
a2 x2
arcsin
x
c
a
dx
1 a x
a 2 x 2 a ln a x c
Майер И.И.
10

11. Методы вычисления неопределенных интегралов.

В рамках изучаемой дисциплины рассматриваются
следующие методы вычисления неопределенных
интегралов:
1. Преобразование подынтегрального выражения
2. Ввод новой переменной интегрирования
3. Метод интегрирования по частям
4. Метод интегрирования рациональной функции
Майер И.И.
11

12.

1. Метод преобразования подынтегрального выражения
(подынтегральной функции)
dx
Пример 1.1. Вычислить
3
x
Решение. Преобразованием подынтегральной функции
сведем интеграл
x
dx
к табличному
3x
dx
1
= dx =
x
3
3
a
x
dx
Майер И.И.
=
x
a
x
a
dx ln x C
1 / 3 x C
ln 1 / 3
12

13.

1. Метод преобразования подынтегрального выражения
(подынтегральной функции)
Пример 1.2. Вычислить
3 x 1
2
dx
Решение. Преобразуем подынтегральную функцию
2
3 x 1
2
3x
2
1
1
3
2
2
x
1 x
8
2
Тогда
x
1
1
8
3 x 1
x
2
dx
8
dx
C
2
2 ln 8
Майер И.И.
13

14.

2. Ввод новой переменной интегрирования.
Вместо переменной интегрирования x вводят новую
Переменную интегрирования t , интеграл сводят к более
простому, например, к табличному.
Пусть x=φ(t), где φ(t) - непрерывная монотонная
функция, имеющая непрерывную производную . Тогда
f ( x )dx
f ( (t )) (t )dt
Майер И.И.
14

15.

2. Ввод новой переменной интегрирования.
Пример 2.1. Вычислить
1 3 x dx .
Решение. Введем новую переменную t=1-3x.
Продифференцируем по х. Тогда dt= - 3dx и dx dt .
3
Подставим найденные выражения в интеграл и получим
1
dt
1 2
t ( 3 ) 3 t dt
1
1
1
1
1
1
2t t
2
2
t
dt
t
c
1
3
3
9
1
2
2
Ответ
1
3
x
dx
(1 3 x ) 1 3 x c
9
Майер И.И.
15

16.

Пример 2.2. Вычислить интеграл
sin( 4 x 2)dx
Решение. Сделаем замену переменной t=4x+2. Тогда
dt
1
dt 4dx, dx , sin( 4 x 2)dx sin tdt
4
4
1
1
1
sin( 4 x 2)dx 4 sin tdt 4 ( cos t ) 4 cos(4 x 2) c
Майер И.И.
16

17.

Пример 2.3. Вычислить
x e
x2
dx
Решение. Введем новую переменную t=x2
Тогда
dt
dt 2 x dx, x dx
,
2
1
1 x2
x2
t
xe dx 2 e dt 2 e c
Майер И.И.
17

18.

3. Метод интегрирования по частям.
Дан интеграл
f ( x )dx
где подынтегральное выражение представляет собой
произведение некоторой функции u(x) на дифференциал другой
функции dv(x), то есть подынтегральное выражение
f ( x )dx u( x )dv( x ).
Тогда
u( x)dv( x) u( x) v( x) v( x)du( x)
Эта формула называется формулой интегрирования по
частям.
Методом интегрирования по частям решены задачи 3.1 и 3.2
Майер И.И.
18

19.

Пример 3.1. Найти
Решение. Пусть
x sin 2 xdx
u x, dv sin 2 x dx
Чтобы применить формулу интегрирования по частям найдем
du и v(x)
cos 2 x
du dx, v dv sin 2 xdx
2
Подставим в формулу интегрирования по частям и получим:
x cos 2 x 1
x cos 2 x 1
x sin 2 xdx 2 2 cos 2 xdx 2 4 sin 2 x c
Майер И.И.
19

20.

Пример 3.2. Найти
Решение. Пусть
Тогда
ln x
dx
2
x
dx
ln x u, dv 2
x
dx
du
,
x
dx
1
v
x2
x
Применив формулу интегрирования по частям, получим
ln x
ln x
dx
ln x 1
x 2 dx x x 2 x x c
Майер И.И.
20

21.

4. Метод интегрирования рациональных функций
Рациональной функцией или рациональной дробью называется
функция которая равна частному от деления двух многочленов
(полиномов) переменной х..
Многочленом называется функция вида
Pn ( x ) a0 a1 x a2 x 2 ... an x n .
Старшая степень n переменной x называется степенью
многочлена, а числа a0 , a1, a2,…an - его коэффициентами
Если Pn(x) - многочлен степени n, а Qm(x) - многочлен степени m,
то функция
Pn ( x )
P( x )
Qm ( x )
называется рациональной функцией или рациональной дробью.
«Правильной» рациональной дробью называют рациональную
функцию, у которой степень n числителя меньше степени m
знаменателя.
Майер И.И.
21

22.

Пример 4.1.
Найти
1 2x
(1 x)2 dx.
Решение. Разобьем сначала интеграл на сумму двух
интегралов, из которых первый найдем сразу, а второй
вычислим после простых преобразований:
1 2x
dx
xdx
( x 1) 1
2
(1 x)2 dx (1 x)2 2 (1 x)2 (1 x) dx 2 (1 x)2 dx;
1 2x
1
2
1
(1 x)2 dx 1 x 2 ln 1 x 1 x 2 ln 1 x 1 x c.
Майер И.И.
22

23.

Пример 4.2 Найти
x2 2x 4
x 2 dx.
Решение. Подынтегральная функция
x2 2x 4
x 2
не является правильной дробью. Преобразуем подынтегральное
выражение
x2 2 x 4
x ( x 2)
dx
x 2 dx x 2 dx 4 x 2
x2
xdx 4 ln x 2
4 ln x 2 c
2
Майер И.И.
23

24.

Пример 4.3. Найти
dx
x( x 8) .
Решение. Представим подынтегральную функцию как сумму
простейших дробей:
1
A
B
x ( x 8)
x
x 8
Приведем правую часть равенства к общему знаменателю. Получим
1
A
B
A( x 8) Bx x( A B) 8 A
.
x( x 8) x x 8
x( x 8)
x( x 8)
Равенство должно выполняться при любых значениях переменной x.
Так как знаменатели равны, то должны быть равны и числители.
Тогда
1
1
A B 0, 8 A 1, A , B .
8
8
Теперь интеграл сведется к сумме двух интегралов
dx
1 dx 1 dx
1
1
1 x 8
x( x 8) 8 x 8 x 8 8 ln x 8 ln x 8 8 ln x c
Майер И.И.
24

25.

• 3.3. Определенный интеграл
• Задача о площади.
• Определенный интеграл –основные
понятия
Майер И.И.
25

26. 3.3. Задача о площади. Понятие определенного интеграла

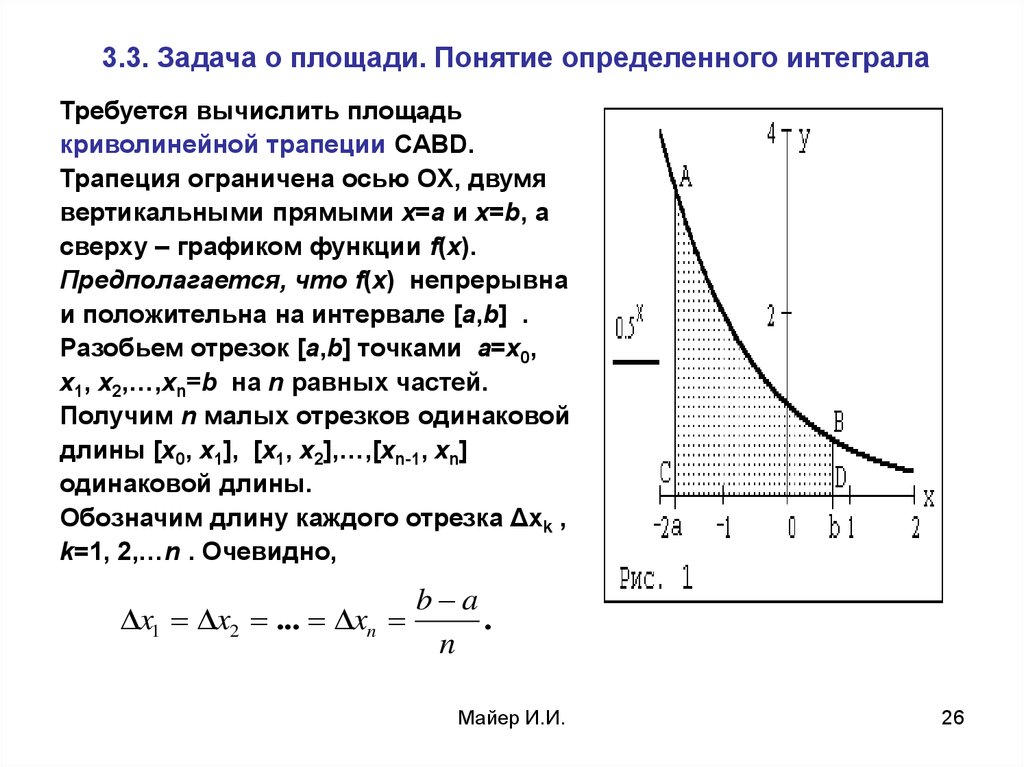
Требуется вычислить площадь
криволинейной трапеции CABD.
Трапеция ограничена осью OX, двумя
вертикальными прямыми x=a и x=b, а
сверху – графиком функции f(x).
Предполагается, что f(x) непрерывна
и положительна на интервале [a,b] .
Разобьем отрезок [a,b] точками a=x0,
x1, x2,…,xn=b на n равных частей.
Получим n малых отрезков одинаковой
длины [x0, x1], [x1, x2],…,[xn-1, xn]
одинаковой длины.
Обозначим длину каждого отрезка Δxk ,
k=1, 2,…n . Очевидно,
x1 x2 ... xn
b a
.
n
Майер И.И.
26

27.

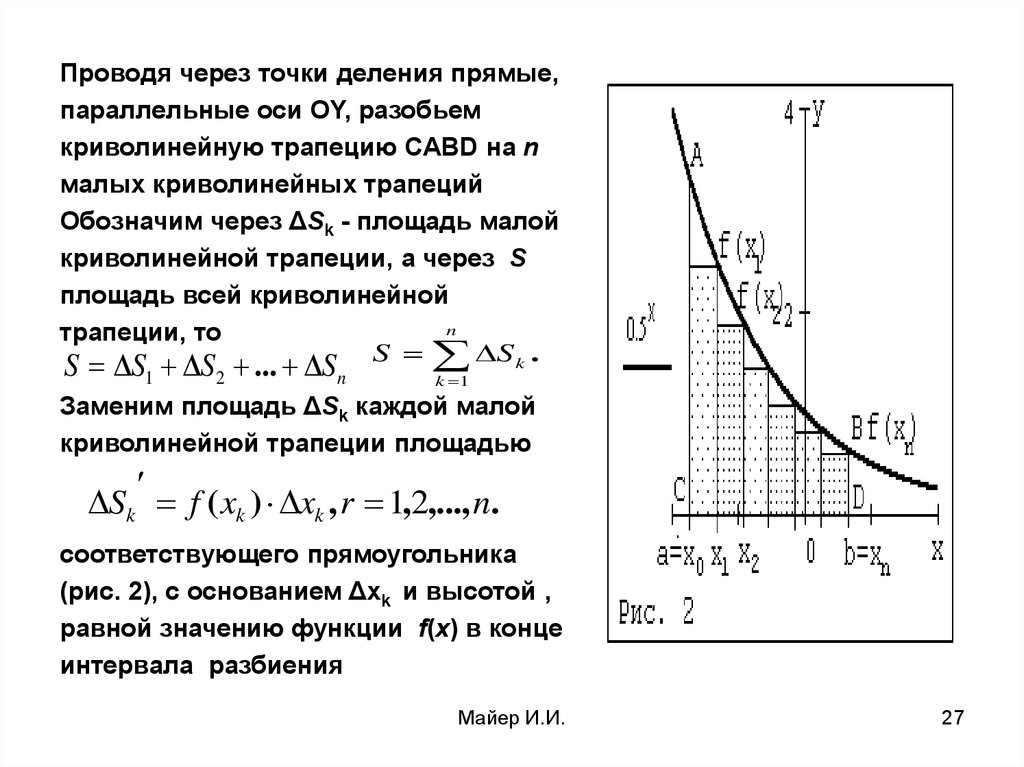
Проводя через точки деления прямые,
параллельные оси OY, разобьем
криволинейную трапецию CABD на n
малых криволинейных трапеций
Обозначим через ΔSk - площадь малой
криволинейной трапеции, а через S
площадь всей криволинейной
n
трапеции, то
S S k .
S S1 S2 ... Sn
k 1
Заменим площадь ΔSk каждой малой
криволинейной трапеции площадью
Sk f ( xk ) xk , r 1,2,..., n.
соответствующего прямоугольника
(рис. 2), с основанием Δxk и высотой ,
равной значению функции f(x) в конце
интервала разбиения
Майер И.И.
27

28.

Очевидно, что Sk Sk и искомую площадь можно приближенно
представить суммой площадей прямоугольников, что равносильно
замене функции f(x) ступенчатой функцией .
n
S f ( x1 ) x1 f ( x2 ) x2 ... f ( xn ) xn f ( xk ) xk .
k 1
Ясно, что чем меньше длина промежутков [xk-1,xk], k=1, 2,…n , тем
точнее ступенчатая фигура приближает (аппроксимирует)
криволинейную трапецию.
За точное значение площади S криволинейной трапеции принимают
предел последовательности площадей ступенчатых фигур, когда
n→∞ и все длины Δxk стремятся к нулю.
b
a
f ( x )dx lim
n
n
k 1
Майер И.И.
f ( xk ) xk .
28

29.

n
Сумма вида
f ( x ) x
k 1
k
называется
k
интегральной суммой
Предел, к которому стремится
последовательность интегральных сумм при
n→∞ , называется определенным интегралом
функции f(x) на отрезке [a, b]. Определенный
интеграл функции f(x) на интервале [a, b]
обозначается символом
b
a
f ( x )dx lim
n
n
f (x
k 1
Майер И.И.
k
) xk
29

30.

• В записи определенного интеграла
b
f ( x) dx.
a
числа a и b - соответственно нижний и верхний пределы
интегрирования, f(x) - подынтегральной функцией,
отрезок [a, b] - область интегрирования.
Если функция f(x) - непрерывна на отрезке [a, b], то
определенный интеграл существует (достаточное условие).
Площадь криволинейной трапеции, ограниченной
непрерывной кривой y= f(x), где f(x)≥0 на всем отрезке [a, b],
численно равна определенному интегралу .
Площадь криволинейной трапеции, ограниченной
непрерывной кривой y= f(x), где f(x) <=0 на всем отрезке [a, b],
численно равна определенному интегралу, взятому со
Знаком минус .
Майер И.И.
30

31.

• 3.4. Вычисление определенного
интеграла. Основные свойства
Майер И.И.
31

32.

• Для вычисления определенного интеграла применяют
формулу Ньютона-Лейбница:
b
f ( x)dx F (b) F (a).
a
• Эта формула справедлива, если f(x) непрерывна на отрезке
[a, b] и F(x) - одна из ее первообразных.
b
• Разность F(b) - F(a) символически обозначают F ( x)
a
• Пример: вычислить определенный интеграл функции 2x на
интервале [0, 1], 1
x
2
dx
0
x
2
x
2
dx ln 2
• Первообразная для 2x ,
1
• Тогда
x
2
dx
0
x
1
2
2
1
1
ln 2 0 ln 2 ln 2 ln 2
Майер И.И.
32

33.

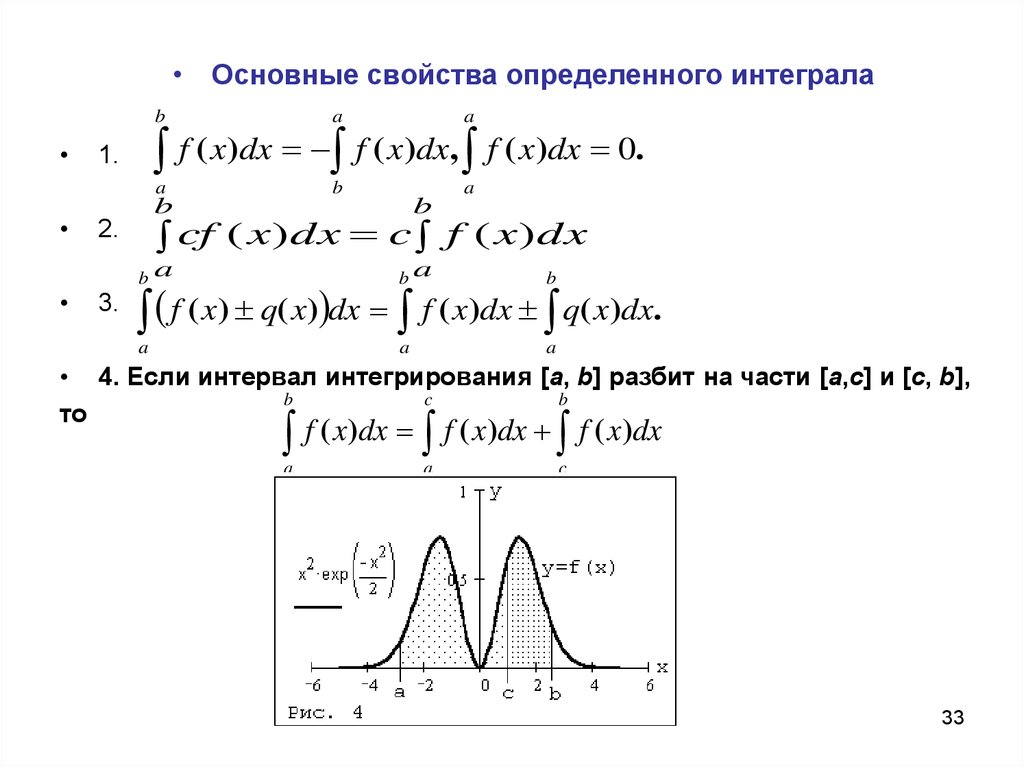
• Основные свойства определенного интеграла
a
b
a
a
b
b
a
ba
b
a
a
cf ( x)dx c f ( x)dx
2.
3.
a
f ( x)dx f ( x)dx, f ( x)dx 0.
1.
b
b
f ( x) q( x) dx f ( x)dx q( x)dx.
a
• 4. Если интервал интегрирования [a, b] разбит на части [a,c] и [c, b],
b
c
b
то
f ( x)dx f ( x)dx f ( x)dx
a
a
c
Майер И.И.
33

34.

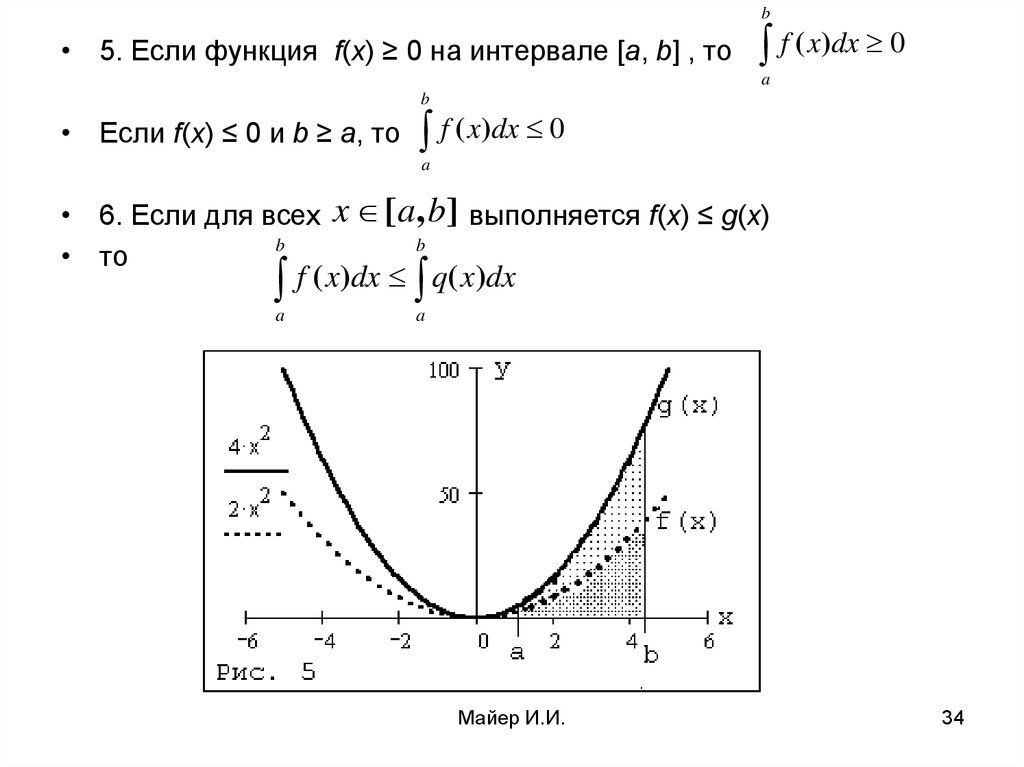
b
• 5. Если функция f(x) ≥ 0 на интервале [a, b] , то
f ( x)dx 0
a
b
• Если f(x) ≤ 0 и b ≥ a, то
f ( x)dx 0
a
• 6. Если для всех
b
• то
x [a, b] выполняется f(x) ≤ g(x)
b
f ( x)dx q( x)dx
a
a
Майер И.И.
34

35.

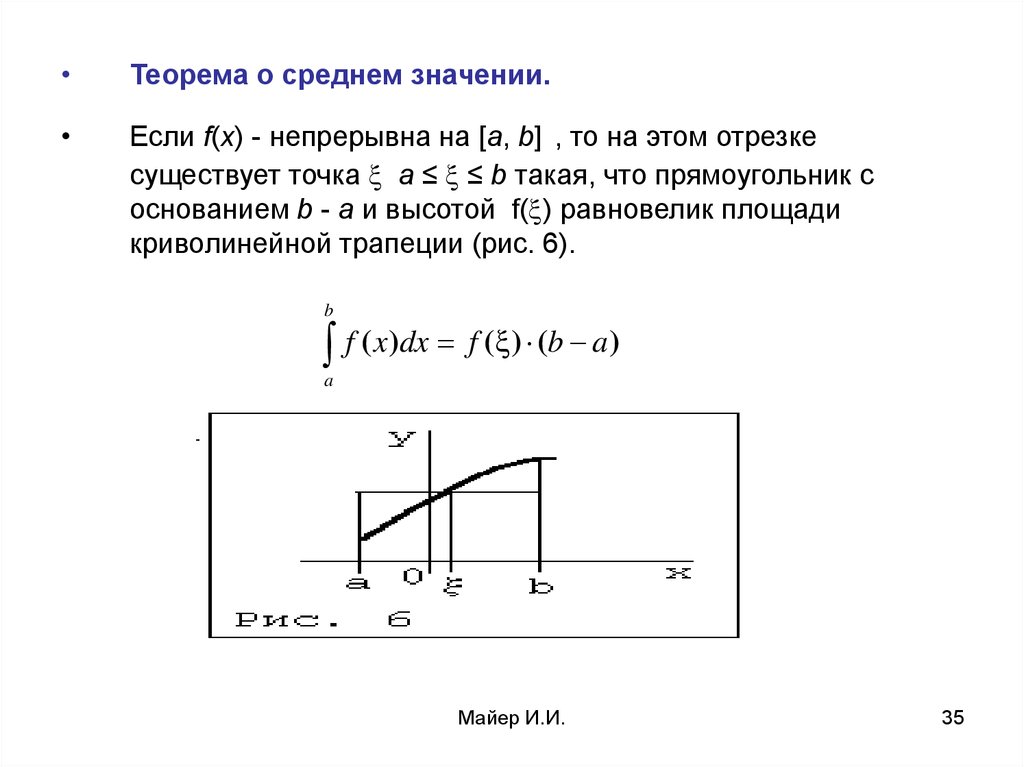
Теорема о среднем значении.
Если f(x) - непрерывна на [a, b] , то на этом отрезке
существует точка a ≤ ≤ b такая, что прямоугольник с
основанием b - a и высотой f( ) равновелик площади
криволинейной трапеции (рис. 6).
b
f ( x)dx f ( ) (b a)
a
Майер И.И.
35

36.

• Примеры вычисления определенного
интеграла
Майер И.И.
36

37.

1
Пример 1. Вычислить
1 x 2 dx
0
Решение. Воспользуемся методом замены переменной. Обозначим
x sin t , тогда
dx cos tdt
При вычислении определенного интеграла методом замены переменной
нет необходимости возвращаться к старой переменной, необходимо
пересчитать пределы интегрирования.
В нашем примере при х=0 t=0 т.к. sin(0)=0; при =0; при x=1
Пределы интегрирования по переменной
Если x = 0, то sin(t) =0; t=0. Если x = 1, то sin t 1 t
2
Тогда
1
1 x 2 dx 2 1 sin 2 t cos tdt
0
0
2
1
cos
2
t
1
sin
2
t
2
2
cos tdt
dt t
0
0
2
2
2 0 4
2
Майер И.И.
37

38.

Пример 2. Вычислить
1
x
3
dx
1
Решение. Подынтегральная функция
y = x3 - нечетная, а область интегрирования
– отрезок, симметричный относительно
начала координат.
Из геометрических соображений
(рис. 7) такой интеграл будет равен
нулю:
3
x
dx
4
x
4
1
1
1 1
0
4 4
Если f(x)- функция четная, а отрезок
интегрирования [-a, a], то можно
вычислить интеграл от 0 до a и
полученный результат удвоить:
1
1
2 31 2
1 x dx 2 0 x dx 3 x 0 3
2
2
Майер И.И.
38

39.

1
• Пример 3. Вычислить
x
x
e
dx
0
• Решение. Воспользуемся формулой интегрирования
по частям b
b
b
udv u v a vdu
a
a
• Возьмем в качестве u
• Тогда du dx, v e x
1
xe dx xe
x
0
x
1
0
x, dv e x dx
1
e dx 1 e e
x
1
x
1
0
e e 1 1
0
Майер И.И.
39

40. 3.5. Несобственные интегралы

Определение термина «Определенный интеграл» было дано в
предположении, что промежуток интегрирования [a, b]
конечен и функция f(x) непрерывна на нем.
Рассмотрим случай, когда промежуток интегрирования
бесконечен. Например, в теории вероятностей большую роль
играют интегралы
e
a
x2
2
a
dx ,
x2
2
xe
dx ,
2
x
e
x2
2
dx
Такие интегралы называют несобственными.
Майер И.И.
40

41.

1
Пример. Функция y 2
x
.
непрерывна на бесконечном интервале
[1, )
Если A - любое конечное число, A > 1 , то существует интеграл
A
dx
1
1
1 x 2
A
который при A имеет предел, равный единице.
Этот предел называют несобственным интегралом функции
y
на бесконечном интервале
1
x2
[1, )
и обозначают символом
dx
1 x 2
Таким образом
dx
dx
1
lim
lim
1
1 x 2 A 1 x 2 A A 1
A
Майер И.И.
41

42.

• Аналогично определяется несобственный интеграл на
интервалах ( , b], ( , )
b
b
c
B
c
f ( x)dx lim f ( x)dx f ( x)dx f ( x)dx f ( x)dx
-
B
• Для несобственных интегралов сохраняются основные свойства
определенных интегралов.
• Так как несобственный интеграл вычисляется как предел, то он
может быть конечным, тогда интеграл сходится, или
бесконечным. Во втором случае несобственный интеграл
расходится
Майер И.И.
42