Элементы математической логики. Интегральное исчисление функций одной переменной и его приложения

1. Прикладная математика и математическая логика

• Лекции –2 часа (1 семестр) и 2 часа (2
семестр)
• Практические занятия – 8 часов (1 семестр)
и 6 часов (2 семестр)
• Экзамен
• Контрольные работы (№ 1 и № 2) по
методичке 15873 (с.16)
• Методические указания 15136 (мат.анализ);
Солдатова Гульнара Тагировна
[email protected]

2. Содержание

• РАЗДЕЛ 1. Элементы математической
логики (задачи 1 и 2)
• РАЗДЕЛ 2. Интегральное исчисление
функций одной переменной и его
приложения (задача 3)
• РАЗДЕЛ
3.
Числовые
и
функциональные
ряды.
Элементы
функционального анализа (задачи 4-6)

3.

Раздел 1. Элементы
математической логики

4.

Алгебра логики (алгебра высказываний,
булева алгебра) – раздел математической
логики, изучающий строение (форму,
структуру) сложных логических высказываний
и способы установления их истинности с
помощью алгебраических методов.
Высказывание – повествовательное
предложение, содержание которого
можно определить как истинное или
ложное.

5.

Простые высказывания называют в
алгебре
логики
логическими
переменными (булевы переменные) и
обозначают
буквами
латинского
алфавита.
Сложные
высказывания
называют
логическими
функциями
(или
логическими выражениями).
Логические переменные и функции
определены
на
множестве
двух
значений {0,1} или {true, false}

6.

• Для образования новых высказываний
используются базовые логические
операции, выражаемые с помощью
логических связок «и», «или», «не».
Логические связки
Конъюнкция
(«и»)
Дизъюнкция
(«или»)
Инверсия
(«не»)

7. 1. Логическое умножение (конъюнкция).

Логические операции
1. Логическое умножение (конъюнкция).
• Объединение двух (или нескольких) высказываний в
одно с помощью союза «и» называется операцией
логического умножения или конъюнкцией.
А
0
0
1
1
В
0
1
0
1
А˄В
0
0
0
1
Пример.
А: «12 делится на 3»
В: «12 делится на 4»,
Тогда А˄В - истинно

8. 2.Логическое сложение (дизъюнкция)

• Объединение двух (или нескольких)
высказываний с помощью союза «или»
называется операцией логического
сложения или дизъюнкцией.
А
0
0
1
1
В
0
1
0
1
А˅В
0
1
1
1
Пример.
А: «12 делится на
3»
В: «12 делится на
5»,

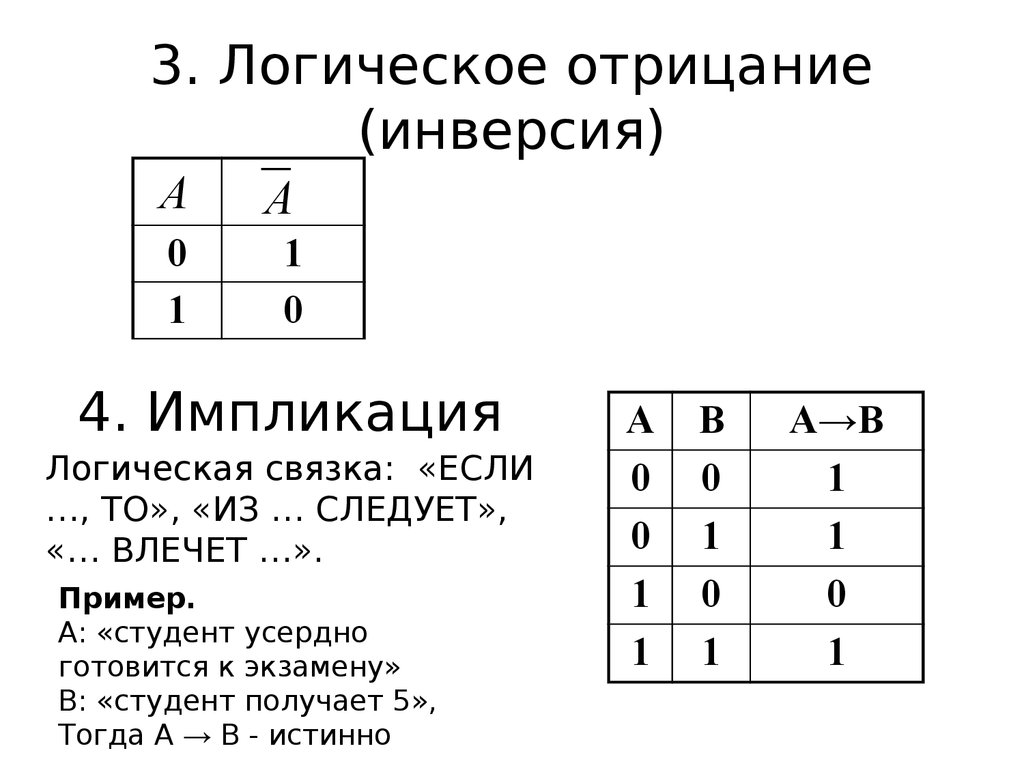
9. 3. Логическое отрицание (инверсия)

A
A
0
1
1
0
4. Импликация
Логическая связка: «ЕСЛИ
…, ТО», «ИЗ … СЛЕДУЕТ»,
«… ВЛЕЧЕТ …».
Пример.
А: «студент усердно
готовится к экзамену»
В: «студент получает 5»,
Тогда А → В - истинно
А
0
0
1
1
В
0
1
0
1
А→В
1
1
0
1

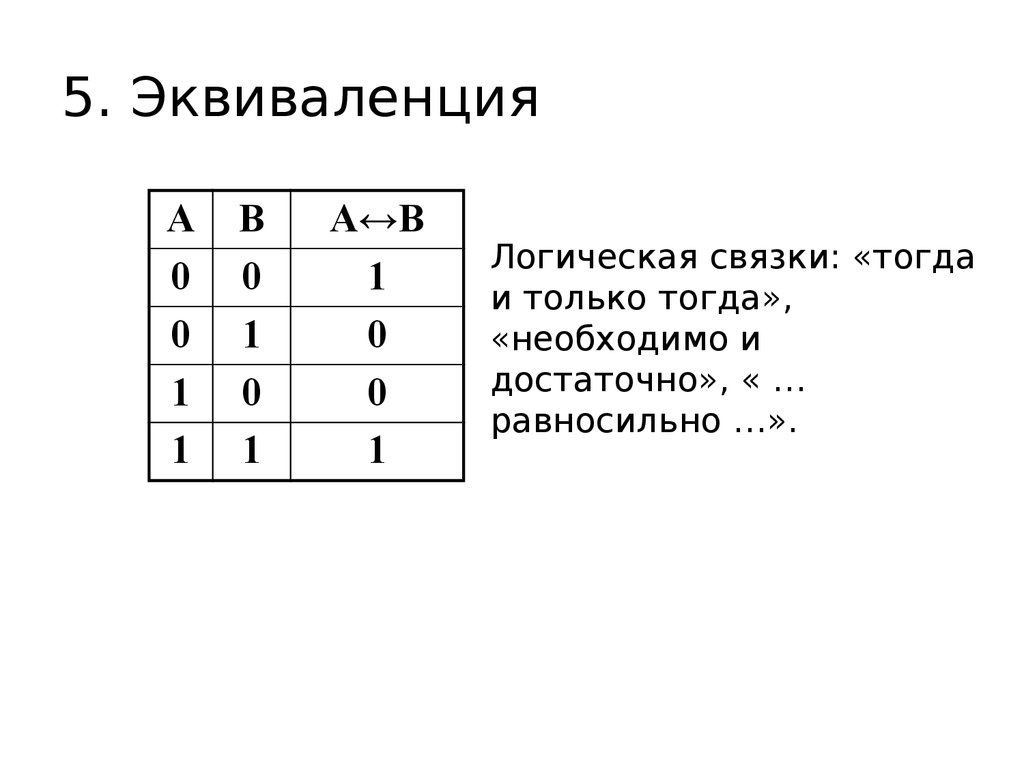
10. 5. Эквиваленция

А
0
0
1
1
В
0
1
0
1
А↔В
1
0
0
1
Логическая связки: «тогда
и только тогда»,
«необходимо и
достаточно», « …
равносильно …».

11. Основные логические тождества

Идемпотентные законы:
1)
A A A
2)
A A A
Коммутативные законы:
3)
4)
5)
A B B A
A B B A
A B B A
Ассоциативные законы:
6)
7)
8)
A B C A B C
A B C A B C
A B C A B C

12.

Дистрибутивные законы:
9)
10)
A B C AB AC
A BC A B A C
Законы Моргана:
11)
A B A B
12)
A B A B
Закон двойного отрицания:
13)
A A
Закон противоречия:
14)
15)
A A 0
Закон исключенного третьего:
A A 1

13.

Законы поглощения:
A A B A
A ( A B) A
Тождества, содержащие константы:
A 0 A
A 1 1
A 0 0
A 1 A
A 0 A
A 1 1
0 A 1
1 A A
A 0 A
A 1 A

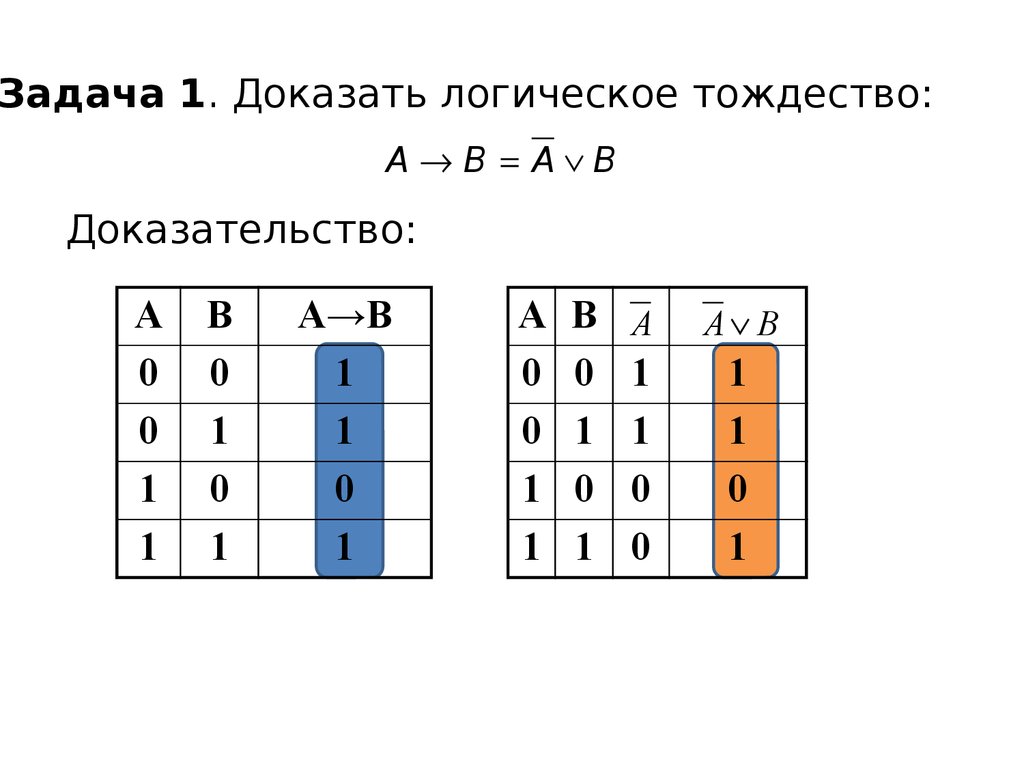
14.

Задача 1. Доказать логическое тождество:
A B A B
Доказательство:
А
0
0
1
1
В
0
1
0
1
А→В
1
1
0
1
А
0
0
1
1
В
0
1
0
1
A
A B
1
1
0
0
1
1
0
1

15. Логические элементы

1. Инвертор – устройство с одним входом
A
и одним выходом, преобразующее
сигнал А в
A
A
2. Конъюнктор – устройство с двумя
A
&
входами и одним выходом
A B
B

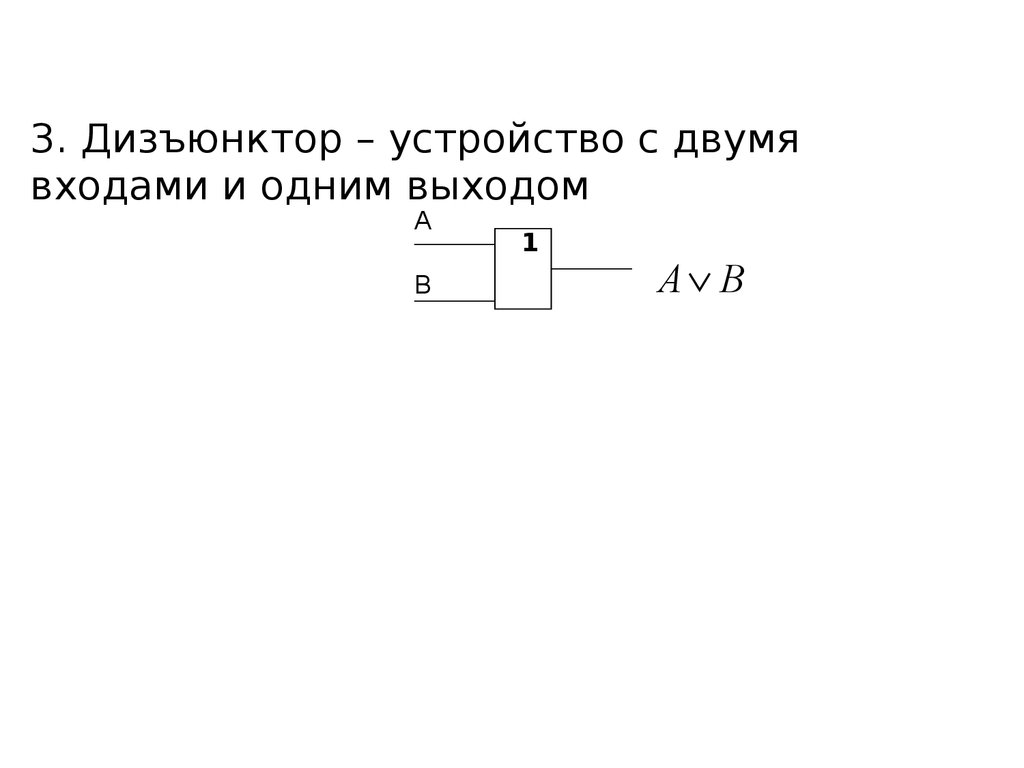
16.

3. Дизъюнктор – устройство с двумя
входами и одним выходом
A
B
1
A B

17.

Задача 2. Представить булеву функцию в
виде СДНФ и начертить схему, реализующую
эту функцию.
y x1 x2 x1 x2 x1 x2
x2 ( x1 x1 ) x1 x2
x2 x1 x2 x2 x1 x2 x2
x2 x1
17

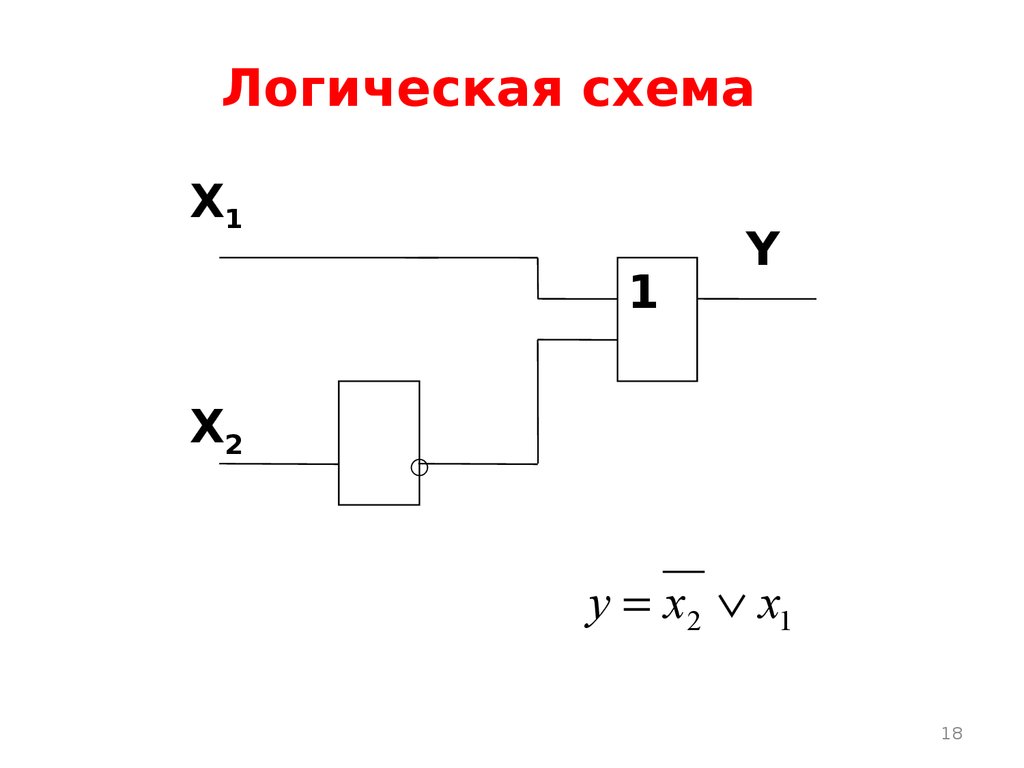
18. Логическая схема

X1
1
Y
X2
y x2 x1
18

19. РАЗДЕЛ 2. Интегральное исчисление функций одной переменной и его приложения

20. Понятие первообразной

Определение.
Функция
F(x),
называется
первообразной для функции f(x), если ее
производная F'(x) равна данной функции, т.е.
F'(x) = f(x). f ( x) 3x 2 .
3
3
F
(
x
)
x
Пример:
x 3x 2 .
т.к.
F ( x) x 3- первообразная,
7
- также первообразная этой же
функции.
Теорема (свойство первообразных).
Если F(x) – первообразная функции f(x), то и
функция
F(x)+C,
где
C
–
произвольная
постоянная, также является первообразной
функции f(x).

21. Понятие неопределенного интеграла

Определение. Множество всех первообразных
данной функции f(x) называется ее
неопределенным
f ( x)dxинтегралом и обозначается
, т.е
f ( x)dx F ( x) C
где C – произвольная постоянная.
Определение. Операция нахождения
неопределенного интеграла от функции
называется интегрированием этой функции.
Определение. График каждой первообразной
называется интегральной кривой.

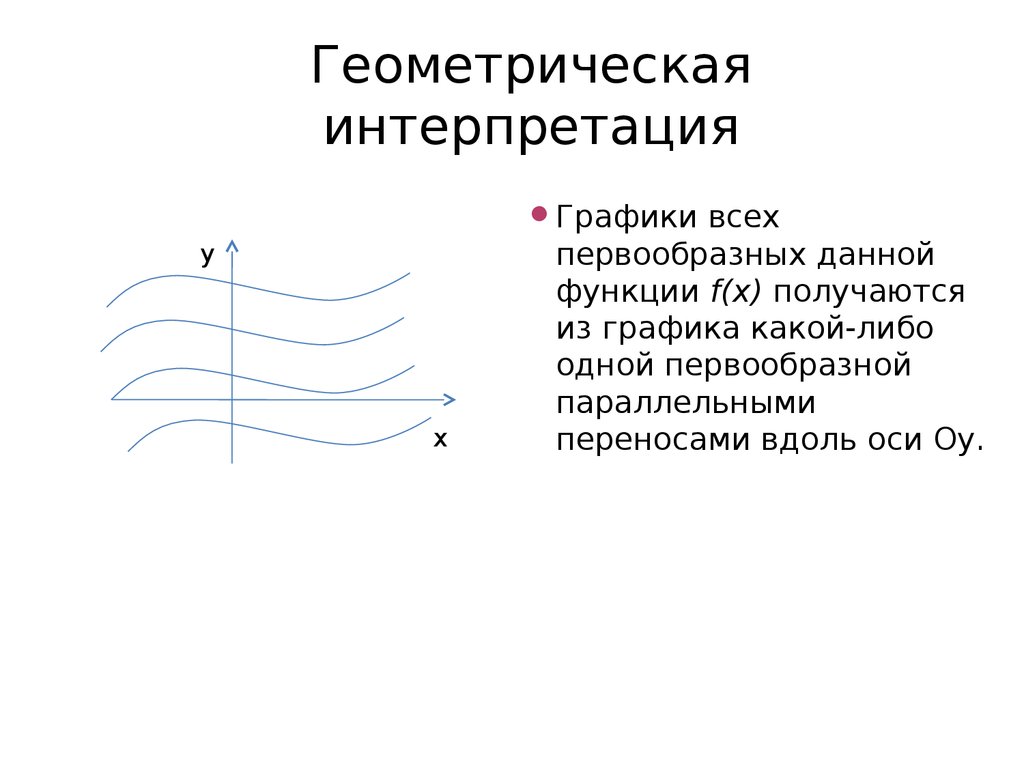
22. Геометрическая интерпретация

Графики всех
y
x
первообразных данной
функции f(x) получаются
из графика какой-либо
одной первообразной
параллельными
переносами вдоль оси Оу.

23. Свойства неопределенного интеграла

1. Производная от неопределенного интеграла
равна подынтегральной функции:
f ( x)dx f ( x)
2. Дифференциал от неопределенного
интеграла равен подынтегральному
d f ( x)dx f ( x)dx
выражению:
3. Постоянный множитель можно выносить за
знак интеграла:
k f ( x)dx k f ( x)dx
4. Интеграл от алгебраической суммы
интегралов равен сумме интегралов от этих
функций:
f ( x) g ( x) dx f ( x)dx g ( x)dx

24. Таблица интегралов

dx x C
x n 1
x dx
C , n 1
n 1
dx
ln x C
x
n
ax
a dx
C
ln a
e
x
x
x
dx e C
sin x dx cos x c
cos x dx sin x c
dx
cos2 x tgx C
dx
sin 2 x ctgx C
dx
1 x2
dx
arcsin x C
1 x 2 arctgx C

25. Методы интегрирования

• Непосредственное интегрирование.
• Интегрирование
методом
замены
переменной (или метод подстановки).
• Интегрирование по частям.

26. Понятие определенного интеграла

27. Понятие определенного интеграла

b
• Выражение f ( x)dx
называют
a
определенным
интегралом функции f(x) на отрезке [ab].
• Если неопределенный интеграл представляет
собой совокупность функций, отстоящих друг от
друга на величину С, то определенный интеграл
– это всегда число, значение которого
определяется видом подынтегральной функции
и значениями верхнего (b) и нижнего (а)
пределов интегрирования.

28. Свойства определенного интеграла

• при смене пределов интегрирования
меняется знак у определенного
b
a
интеграла
f ( x)dx f ( x)dx
a
b
• если пределы интегрирования равны
a
между
собой,
то
определенный
f
(
x
)
dx
0
a
интеграл равен нулю
b
c
b
• если точкаf (сx)принадлежит
отрезку [ab],
dx
f
(
x
)
dx
f
(
x
)
dx
то выполняется
равенство
a
a
c

29. Формула Ньютона -Лейбница

• Чтобы
вычислить
определенный
интеграл
необходимо
найти
его
первообразную
(неопределенный
интеграл) и подставить пределы
интегрирования
b
f ( x)dx F (b) F (a)
a