Интегральное исчисление функции одной переменной и нескольких переменных

1. МАТЕМАТИКА 2.1

tpu.ru
МАТЕМАТИКА 2.1
Интегральное исчисление функции одной переменной
Интегральное исчисление функции нескольких переменных
Обыкновенные дифференциальные уравнения и системы
2024/25 уч. год
Ефремова Оксана Николаевна
Доцент Отделения математики и
математической физики

2.

Рейтинг-лист дисциплины
ЛЕКЦИИ
ПРАКТ. ЗАНЯТИЯ
ФОРМА КОНТРОЛЯ
48 ЧАС.
48 ЧАС.
ЭКЗАМЕН
Мероприятие
ИДЗ (5 шт.)
10
Контрольные (3 шт.)
40
РТ (2 шт.)
20
Экзамен
30
Учебники и задачники
балл
Конспект лекций (заполняется в течение семестра)
Щипачев В.С. Высшая математика. 7-е изд., стер. - М.: 2005.— 479 с.
Берман Г.Н. Сборник задач по курсу математического анализа
Запорожец Г.И. Руководство к решению задач по математическому анализу
Электронный курс
https://stud.lms.tpu.ru/course/vi
ew.php?id=4812
Математика 2.3

3.

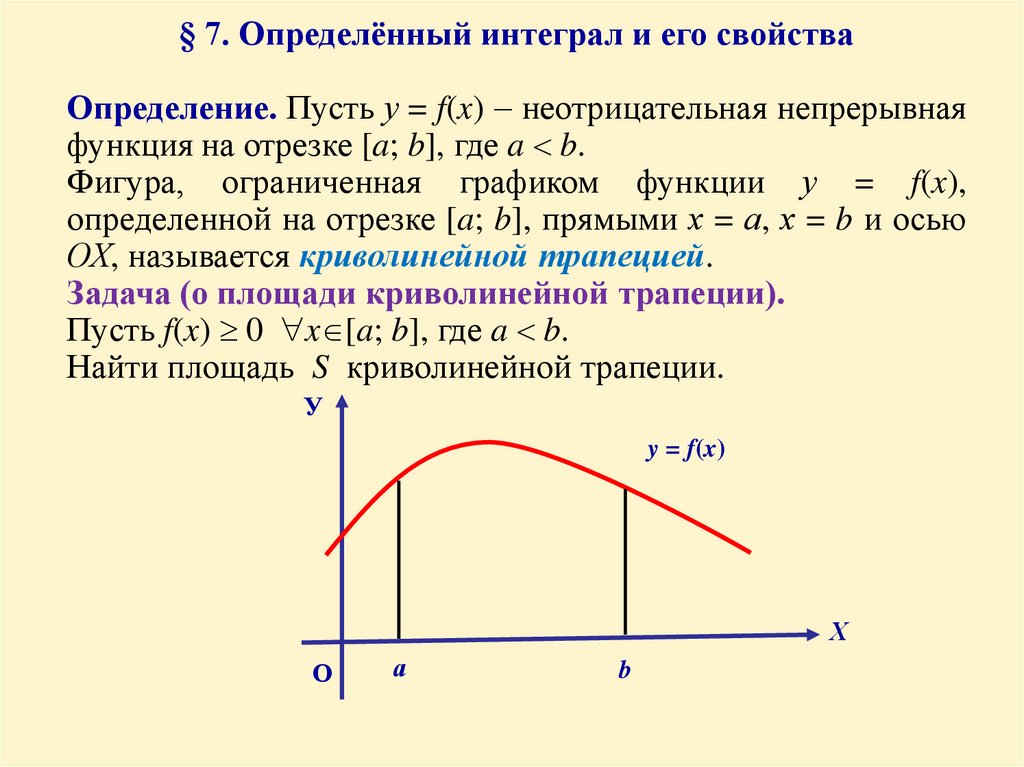
§ 7. Определённый интеграл и его свойства
Определение. Пусть у = f(x) неотрицательная непрерывная
функция на отрезке [a; b], где a b.
Фигура, ограниченная графиком функции у = f(x),
определенной на отрезке [a; b], прямыми х = а, х = b и осью
ОХ, называется криволинейной трапецией.
Задача (о площади криволинейной трапеции).
Пусть f(x) 0 x [a; b], где a b.
Найти площадь S криволинейной трапеции.
У
y = f(x)
Х
О
а
b

4.

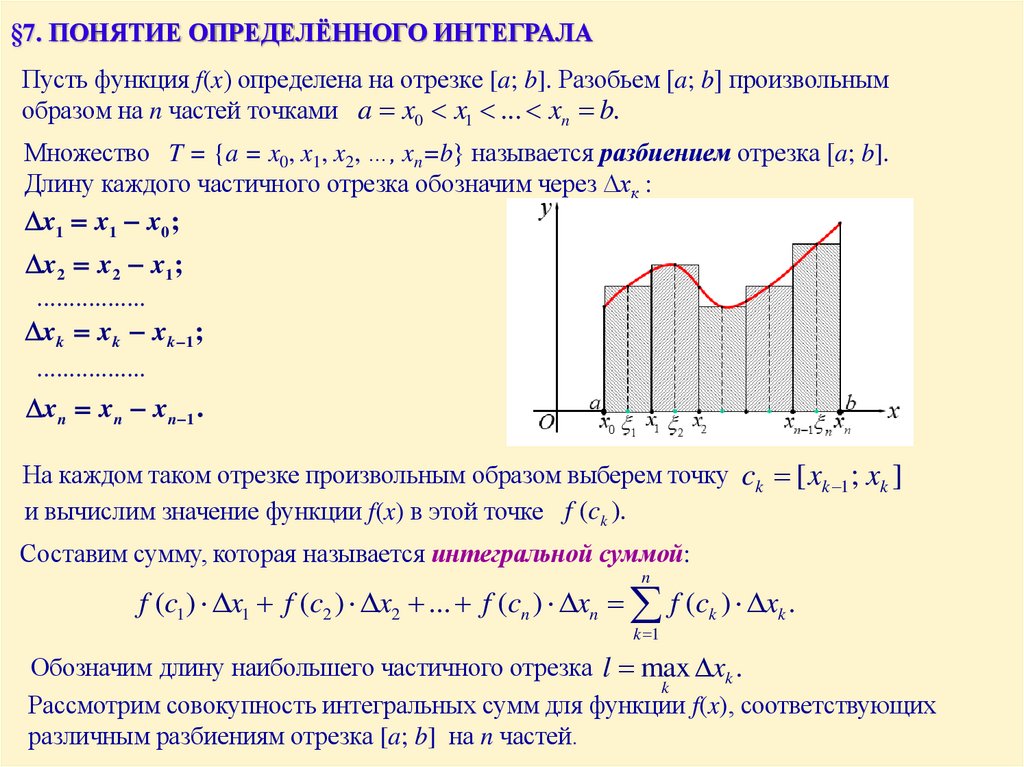
§7. ПОНЯТИЕ ОПРЕДЕЛЁННОГО ИНТЕГРАЛА
Пусть функция f(x) определена на отрезке [a; b]. Разобьем [a; b] произвольным
образом на n частей точками a x0 x1 ... xn b.
Множество T = {a = x0, x1, x2, …, xn=b} называется разбиением отрезка [a; b].
Длину каждого частичного отрезка обозначим через хк :
x1 x1 x0 ;
x2 x2 x1 ;
.................
x k x k x k 1 ;
.................
x n x n x n 1 .
На каждом таком отрезке произвольным образом выберем точку ck [ xk 1; xk ]
и вычислим значение функции f(x) в этой точке f (ck ).
Составим сумму, которая называется интегральной суммой:
n
f (c1 ) x1 f (c2 ) x2 ... f (cn ) xn f (ck ) xk .
k 1
Обозначим длину наибольшего частичного отрезка l max xk .
k
Рассмотрим совокупность интегральных сумм для функции f(x), соответствующих
различным разбиениям отрезка [a; b] на n частей.

5.

При неограниченном увеличении числа n длина l наибольшего из частичных отрезков
соответствующего разбиения будет стремиться к нулю.
Определение. Если существует конечный предел интегральных сумм
n
f (c ) x
k 1
k
k
при n ,
не зависящий ни от способа разбиения отрезка [a; b] на частичные отрезки,
ни от выбора точек на этих отрезках, то этот предел называется определённым
интегралом от функции f(x) на отрезке [a; b] и обозначается так
b
f ( x)dx.
a
f ( x ) - подынтегральная функция;
f ( x )dx - подынтегральное выражение;
x - переменная интегрирования;
a - нижний предел интегрирования;
.
b - верхний предел интегрирования.
пропустить 0.5 страницы

6.

Геометрический смысл неопределённого интеграла:
Площадь криволинейной трапеции, ограниченной сверху кривой непрерывной
функции y = f(x), с основанием [a; b], где f(x) 0, x [a; b], находится
b
по формуле:
s f ( x)dx
a
Физический смысл неопределённого интеграла:
а) путь, пройденный точкой за время от t1 до t2 со скоростью v = v(t):
b
S v(t )dt
a
б) масса неоднородного стержня длиной от x1 до x2 с линейной плотностью = (x):
x2
M ( x)dx
x1
в) работа по перемещению точки под действием переменной силы F =F(x)
b
из точки a в точку b:
A F ( x)dx
a
г) количество вещества, образовавшегося в процессе хим. реакции: q =q(t) – скорость
реакции, t1 – время начала, t2 – время окончания реакции:
t2
Q q (t )dt
t1

7.

Определение.
Функция
f(x),
для
которой
на
отрезке
[a; b] существует определенный интеграл, называется интегрируемой на
этом отрезке.
ТЕОРЕМА 1. (необходимое условие интегрируемости)
b
Если f ( x)dx существует, то функция f(x) ограничена на отрезке [a; b].
a
пропустить 0.5 страницы на пример
ТЕОРЕМА 2. (достаточное условие интегрируемости)
Для того, чтобы функция f(x) была интегрируема на [a; b], достаточно,
чтобы выполнялось одно из условий:
1) f(x) непрерывна на отрезке [a; b];
2) f(x) монотонна на отрезке [a; b];
3) f(x) ограничена на отрезке [a; b] и имеет на нём конечное число точек
разрыва первого рода.

8.

§8. СВОЙСТВА ОПРЕДЕЛЁННОГО ИНТЕГРАЛА
Свойство 1.
b
dx b a
a
Свойство 2.
a
f ( x )dx 0
Оставить место для рисунка
после свойства 1, 4 и
для доказательства 5-7 строк
a
Свойство 3.
b
a
a
b
f ( x )dx f ( x )dx
Свойство 4 (свойство линейности).

9.

Свойство 5.
Оставить место для рисунка
после каждого свойства и
для доказательства 5-7 строк
b
f ( x ) 0 x [a; b] f ( x )dx 0
a
Свойство 6.
b
b
a
a
f ( x ) g( x ) x [a; b] f ( x )dx g( x )dx
Свойство 7 (оценка интеграла).
b
m (b a ) f ( x )dx M (b a )
a
Свойство 8 (теорема о среднем значении).
b
c [a; b]: f ( x )dx f (c ) (b a )
a
Оставить место для
примера после 7

10.

Свойство 9.
1. Пусть y = f(x) непрерывная четная на [ a; a] функция, тогда
a
a
a
0
f ( x)dx 2 f ( x)dx
2. Пусть y = f(x) непрерывная нечетная на [ a; a] функция,
тогда
a
f ( x)dx 0
a
Оставить место для
двух рисунков

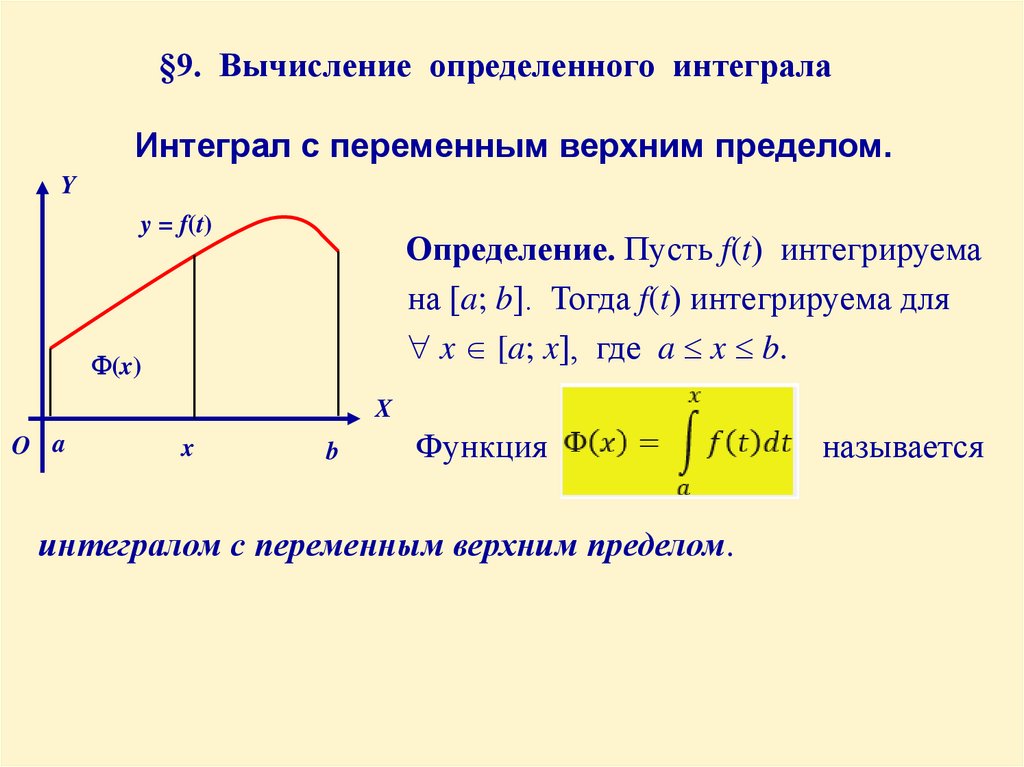
11. §9. Вычисление определенного интеграла

Интеграл с переменным верхним пределом.
Y
y = f(t)
Определение. Пусть f(t) интегрируема
на [a; b]. Тогда f(t) интегрируема для
x [a; x], где a x b.
(x)
X
O a
x
b
Функция
интегралом с переменным верхним пределом.
называется

12.

Теорема (о производной определенного интеграла по переменному
верхнему пределу).
Производная интеграла от непрерывной функции по переменному верхнему
пределу существует и равна значению подынтегральной функции в точке,
равной верхнему пределу:
Доказательство
Оставить 1 страницу

13.

Оставить 5 строк на
пример

14.

§10. МЕТОДЫ ВЫЧИСЛЕНИЯ ОПРЕДЕЛЁННОГО ИНТЕГРАЛА
10.1. Основная формула интегрального исчисления
ТЕОРЕМА 1
Пусть функция f(x) непрерывна на отрезке [a; b], и функция F(x) является какойлибо её первообразной на этом отрезке, тогда справедливо равенство
b
f (x )dx F (b) F (a)
ДОКАЗАТЕЛЬСТВО
a
пропустить 18 строчек
b
f (x )dx F (x ) a F (b) F (a)
a
ПРИМЕР 1
пропустить 12 строчек
b
Формула Ньютона Лейбница

15.

10.2. Замена переменной в определённом интеграле
ТЕОРЕМА 2
Если функция f(x) непрерывна на отрезке [a; b], функция x = u(t) дифференцируема
на отрезке [ ; ] и удовлетворяет условиям:
u (t ) непрерывна на отрезке
2. u( ) a,
u( ) b
1.
3. u(t) монотонна на отрезке
[ ; ]
[ ; ]
то имеет место равенство
b
a
f (x )dx f u (t ) u (t )dt
ДОКАЗАТЕЛЬСТВО
пропустить 25 строчек
ПРИМЕР 2
пропустить 15 строчек
формула замены переменной
в определённом интеграле

16.

10.3. Интегрирование по частям в определённом интеграле
ТЕОРЕМА 3.
Если функции u = u(x) и v = v(x) непрерывны вместе со своими производными
на отрезке [a; b], то имеет место равенство:
b
b
udv uv vdu
b
a
a
ДОКАЗАТЕЛЬСТВО
пропустить 25-30 строчек
a
- формула интегрирования
по частям
в определённом интеграле

17. Декартова и полярная система координат

Декартова система координат (ДСК)
y
M
y
x
O
x
O – начало координат;
Ox, Oy – координатные оси.
(x, y) – координаты точки M;
x – абсцисса точки M,
y – ордината точки M.
Полярная система координат (ПСК)
y
M
r
O
x
P
пропустить 1 страницу
O – полюс; OP – полярная ось.
(r, φ) – полярные координаты M .
r – полярный радиус точки M ;
φ – полярный угол точки M.
Cвязь декартовых и полярных
координат:
x = rcosφ, y = rsinφ .