Интегральное исчисление функций одной переменной

1. Интегральное исчисление функции одной переменной

НЕОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ
Первообразная. Неопределенный интеграл и его
свойства.
Таблица основных интегралов.
Интегрирование методом замены переменной /
подведением под дифференциал. Метод
интегрирования по частям.
Интегрирование рациональных / тригонометрических
функций, некоторых иррациональностей.
ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ
Определенный интеграл и его свойства.
Геометрический смысл определенного интеграла.

2. Интегральное исчисление функции одной переменной

Формула Ньютона-Лейбница.
Метод замены переменной. Метод интегрирования
по частям.
Приложение определенных интегралов: вычисление
площадей фигур, длин дуг, объемов тел вращения.
НЕСОБСТВЕННЫЙ ИНТЕГРАЛ

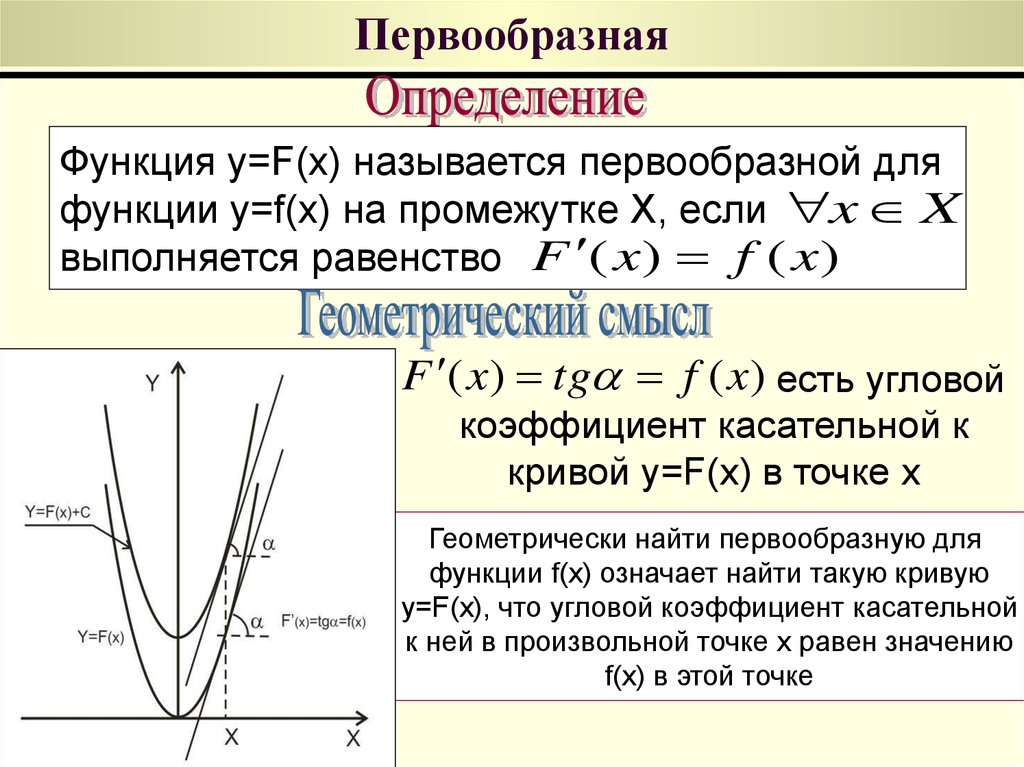
3. Первообразная

Функция y=F(x) называется первообразной для
функции y=f(x) на промежутке X, если x X
выполняется равенство F ( x ) f ( x )
F ( x) tg f ( x) есть угловой
коэффициент касательной к
кривой y=F(x) в точке x
Геометрически найти первообразную для
функции f(x) означает найти такую кривую
y=F(x), что угловой коэффициент касательной
к ней в произвольной точке x равен значению
f(x) в этой точке

4. Первообразная

(об общем виде первообразной)
Если F(x) - первообразная для функции y=f(x)
на промежутке X, то все первообразные для
функции у=f(x) имеют вид F(x)+c, где с –
- произвольная постоянная

5. Неопределенный интеграл

Совокупность всех первообразных для функции f(x)
на промежутке Х называется интеграл от функции f(x)
f ( x) dx
и обозначается
знак интеграла
f ( x ) подынтегральная функция
f ( x ) dx подынтегральное выражение
f ( x) dx F ( x) c
F ( x ) некоторая первообразная для функции f(x)
с произвольная постоянная

6. Свойства неопределенного интеграла

1. Производная неопределенного интеграла равна
подынтегральной функции ( f ( x ) dx ) f ( x )
2. Дифференциал неопределенного интеграла равен
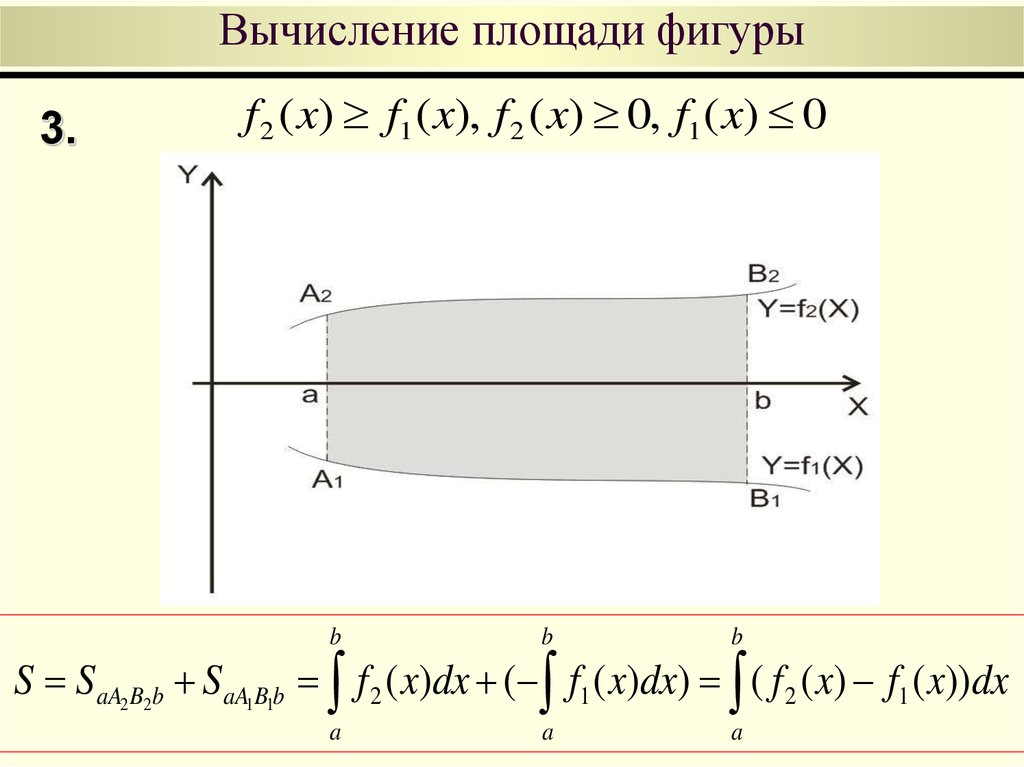
подынтегральному выражению d ( f ( x)dx) f ( x)dx
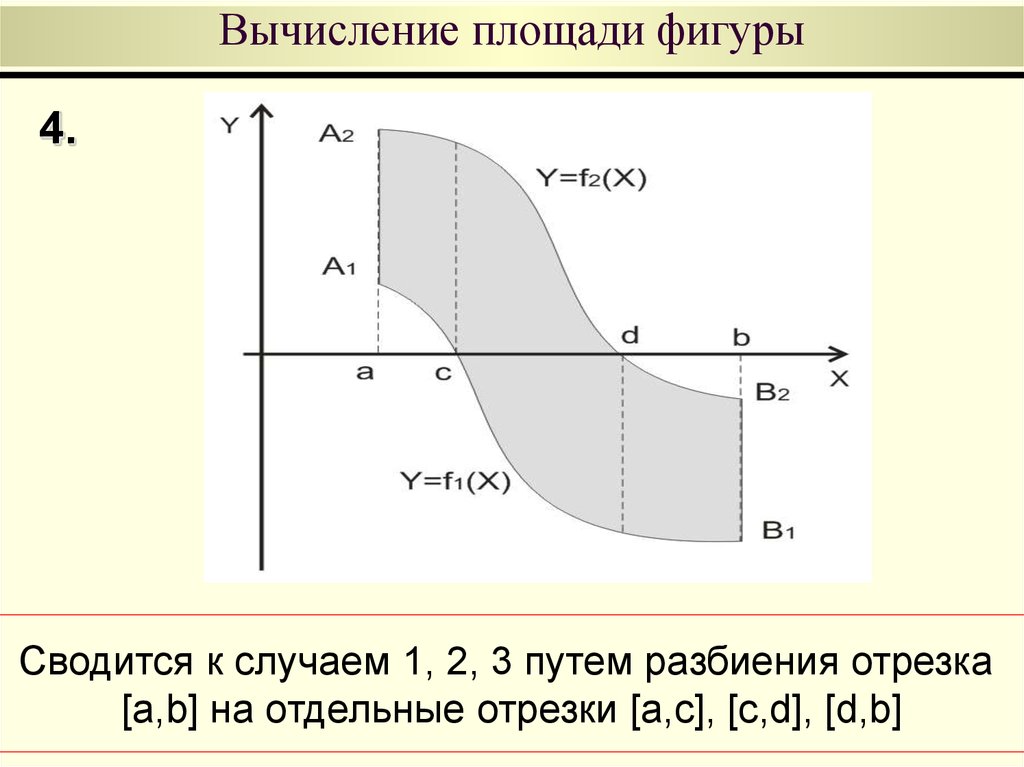
3.
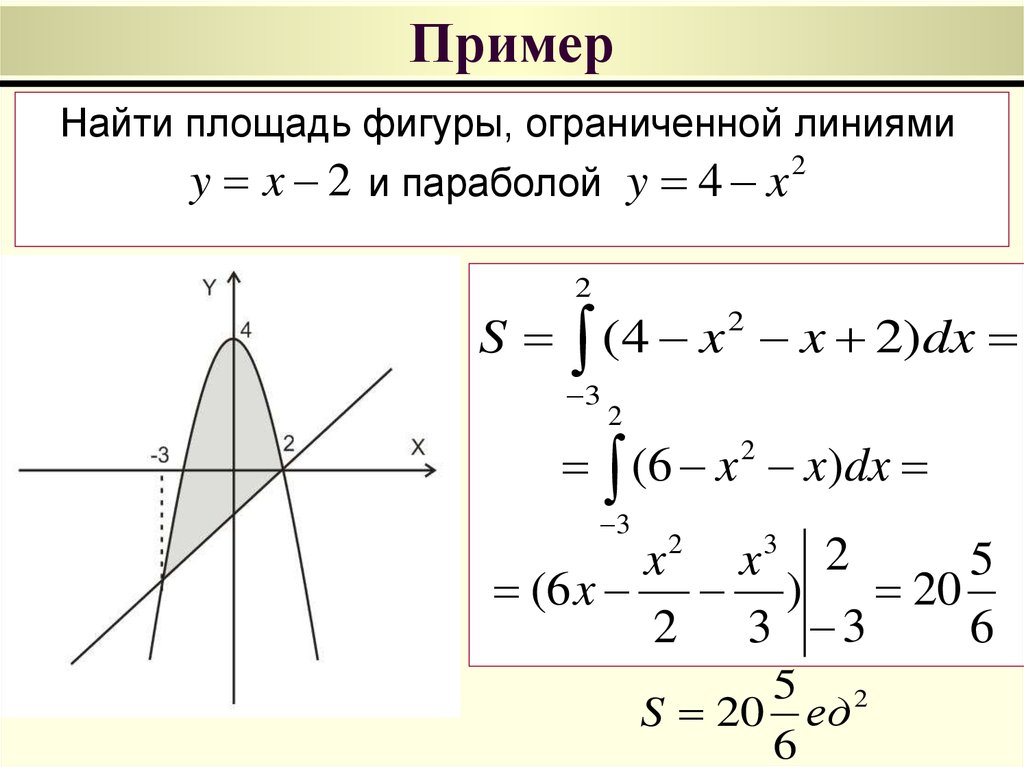
dF ( x) F ( x) c
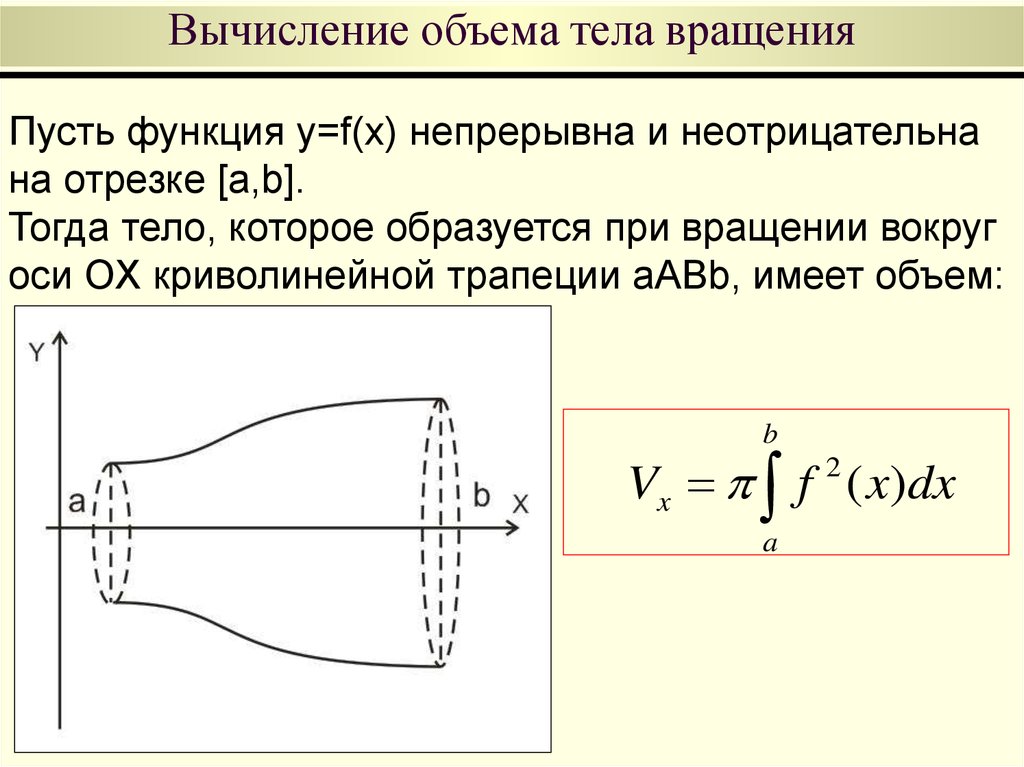
4. Постоянный множитель можно вынести за знак
интеграла k f ( x)dx k f ( x) dx k const
5.
( f ( x) g ( x)) dx
f ( x) dx g ( x)dx
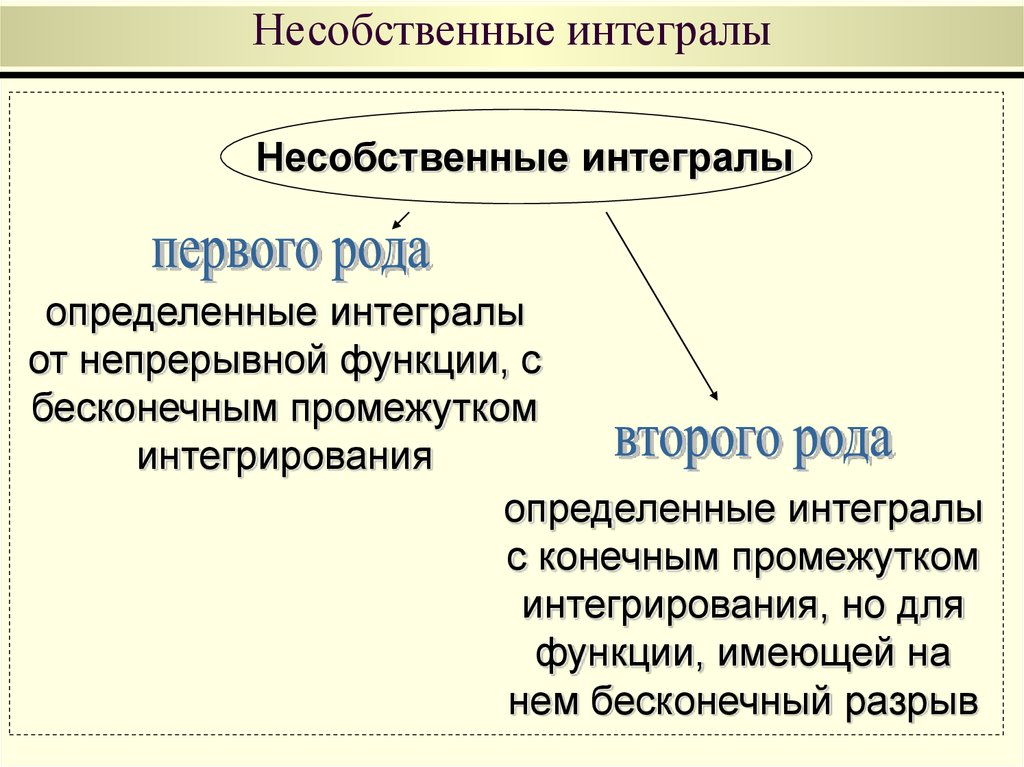
Это свойство справедливо для любого конечного
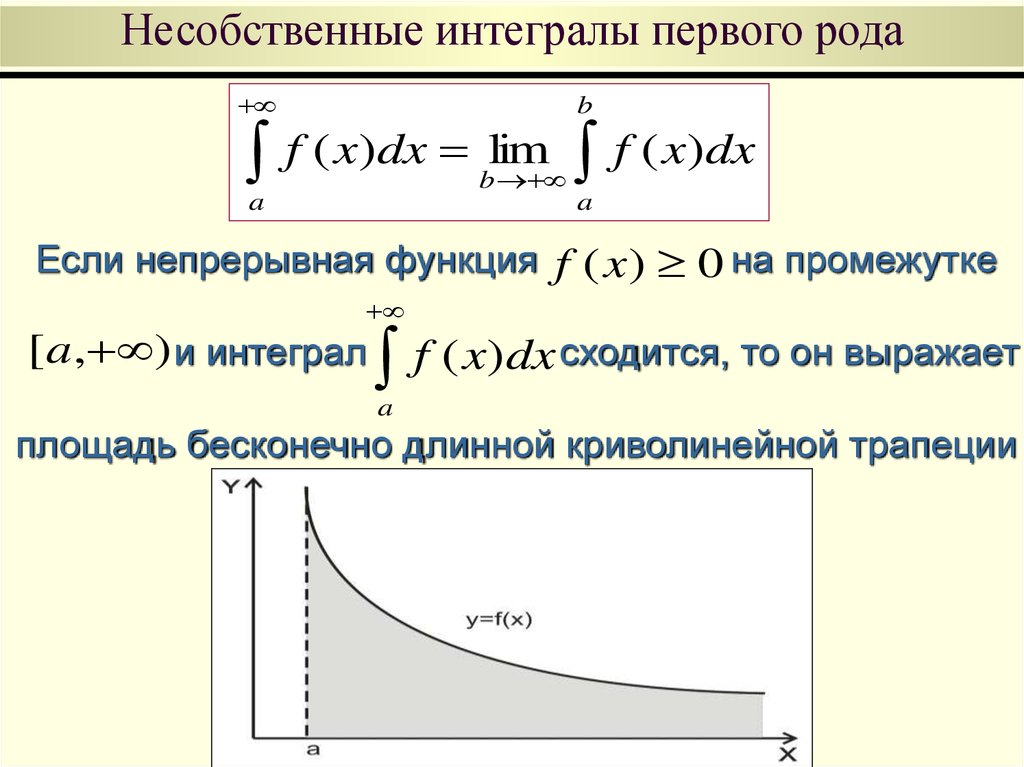
числа слагаемых

7. Таблица основных интегралов

dx x c
1
dx tgx c
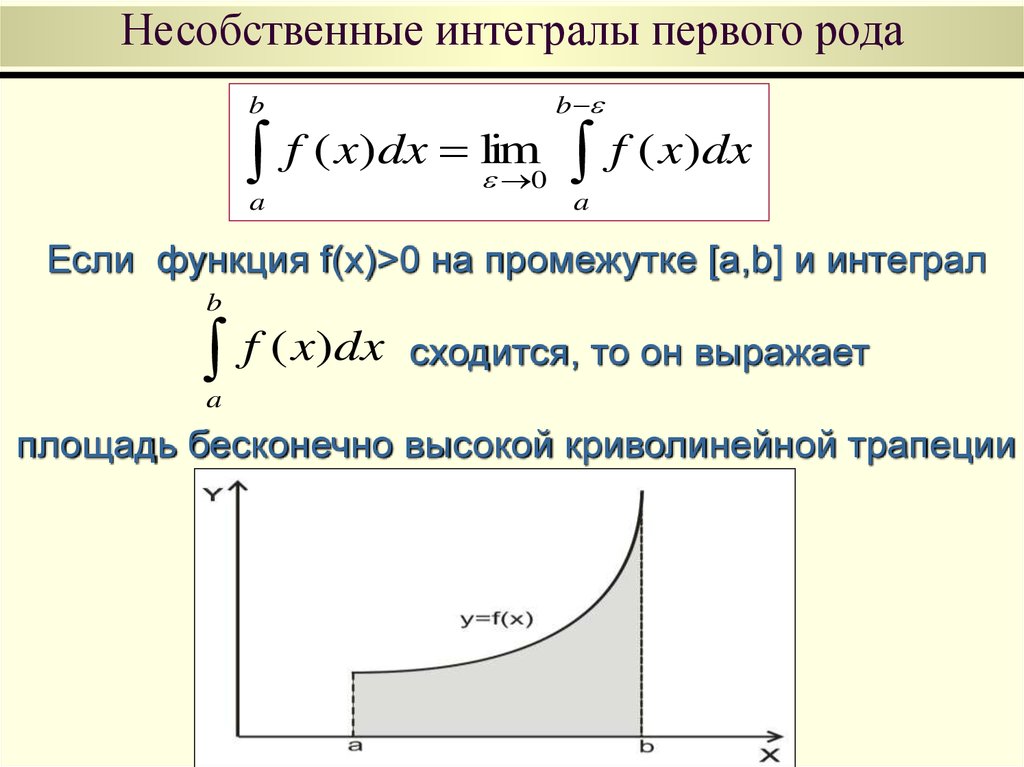
n 1
2
x
cos x
n
c
n 1 x dx
1
n 1
dx ctgx c
2
1
sin x
dx
ln
x
c
n 1
1
x
x
dx arcsin c
x
2
2
a
a
a
0
,
x
a
x
a dx ln a c, a 1
1
1
x
dx arctg c
2
2
x
x
a x
a
a
e
dx
e
c
1
1
x a
dx
ln
c
2
2
x a
2a x a
sin xdx cos x c
cos xdx sin x c
1
x2 k
dx ln x x 2 k c

8. Примеры табличного интегрирования

1.
2 33 x 2 5 x
x
3
1
6
1
2
2 3x 5 x
x
3
2
1
2
3
2
5
6
dx 2 x dx 3x dx
x
1
5 x dx 2
3 5 ln x c 4
186 x 5 ln x c
1
1
x
2
6
1
x
dx
2
3
dx
(1 x ) x
1
1
1
1
2. 4 2 2 2
dx ( 2 2 )dx 2 dx 2 dx
x x
x ( x 1)
x x 1
x
x 1
1
arctgx c
x
2
2

9. Примеры табличного интегрирования

1
5
1 5
2
2
3. (2 x 2 e )dx 2 x dx 2 dx dx e dx
x
x
x
x
1
3
1
4 2 1
2
2
2
2 x dx x dx 5 dx e dx x 5 ln x e 2 x c
x
3
x
2
2
4.
2
4 x2
x 4
dx. 2
1
x2 4
dx 2
1
4 x2
dx
x
2 ln x x 4 2 arcsin c
2
2
5. sin 3 x e
1 2 x
e c
2
2 x
dx. sin 3xdx e
2 x
1
dx cos 3x
3

10. Интегрирование методом замены переменной

Пусть функция x (t ) определена и
дифференцируема на промежутке T и X – множество
ее значений, на котором определена функция f(x).
Тогда f ( x)dx f ( (t )) (t )dt (1)

11. Пример

x
1 x dx
x t
2
x
t
t
1 1
2
1 x dx x t 1 t 2 2tdt 2 1 t 2 dt
dx 2tdt
1
2 (1
)dt 2(t arctgt ) c 2 x 2arctg x c
2
1 t

12. Интегрирование методом замены переменной

(о линейной замене переменной)
1
Если f ( x)dx F ( x) c , то f (ax b)dx F (ax b) c
a
1 5
x
dx
x
c
5
4
1 1
1
5
5
(2 x 1) dx 2 5 (2 x 1) c 10 (2 x 1) c
4

13. Метод подведения под дифференциал

Формулой замены переменной (1) можно
пользоваться и справа налево, то есть
f ( (t )) (t )dt f ( (t )) d (t ) f ( x)dx
Этот метод называется методом подведения
под дифференциал
sin x
1
1
tgxdx cos x dx cos x sin xdx cos x (cos x) dx
1
d cos x ln cos x c
cos x

14. Метод интегрирования по частям

Пусть функции u=u(x); v=v(x) дифференцируемые
функции на промежутке X. Тогда на промежутке X
выполняется формула интегрирования по частям
udv uv vdu (2)

15. Типы интегралов, удобно вычисляемых методом интегрирования по частям

kx
P
(
x
)
e
dx
P( x) sin kxdx
P( x) cos kxdx
P(x) – многочлен, k – некоторое число
Удобно положить в качестве u=P(x), а за dv обозначить
все остальные сомножители
P( x) arcsin xdx P( x) arccos xdx P( x) ln xdx
P( x)arctgxdx P( x)arcсrcсtg
Удобно положить в качестве P(x)dx= dv, а за u
обозначить все остальные сомножители
ax
e
sin bxdx
u e
ax
ax
e
cos bxdx a, b - числа
, dv - все остальные сомножители. Применить
дважды операцию интегрирования по частям.

16. Примеры

u 2 x 1 dv e3 x e3 x
3x
e
3x
3x
(
2
x
1
)
e
dx
(2 x 1) 2dx
e
3
du 2dx v
3
3
e3 x
e3 x
1
2 3x
3x
(2 x 1)
2dx (2 x 1)e e с
3
3
3
9
u ln x
ln xdx du 1 dx
x
x ln x x c
dv dx
1
x ln x x dx
v x
x

17. Интегрирование рациональных функций

R
(
x
)
dx
P( x)
R( x)
- рациональная функция, где
Q( x)
P( x) a0 x a1 x
n
n 1
... an 1 x an ,
ai R, i 0, n - многочлен степени n
Q ( x )- многочлен (возможно степени, отличной от n)
P( x)
Если дробь
неправильная, то можно выполнить
Q( x)
деление с остатком и представить R(x) в виде суммы
некоторого многочлена и правильной дроби

18. Пример

3
x3
dx
2
x 4
x
R( x) 2
- неправильная дробь
x 4
3
x
4x
R( x) 2
x 2
x 4
x 4
3
x
4x
4x
x 2 4 dx ( x x 2 4 )dx xdx x 2 4 dx
2
1 2
( x 4)
1 2
1
2
x 2 2
dx x 2 2
d ( x 4)
2
x 4
2
x 4
1 2
2
x 2 ln x 4 c
2

19. Интегрирование рациональных функций

P
(
x
)
Всякая правильная дробь
может быть
Q( x)
представлена в виде суммы простейших
дробей вида:
A
B
Cx D
Mx N
,
, 2
, 2
n
m
x a ( x a) x px q ( x px q)
где A,B,C,D,M,N – некоторые действительные
числа;
a – число, при котором Q(x)=0;
2
p,q – числа, при которых x px q 0

20. Интегрирование тригонометрических функций

R(sin
x, cos x ) dx
R- рациональная функция
Универсальная тригонометрическая подстановка
Замена сводит подынтегральную функцию к
рациональной дроби
2tg
x
t tg
2
x
2t
sin x
2
x
1 t
1 tg 2
2
2
x 2arctgt
x
x
1 tg
2
1 t
2
cos x
2
x
1 t
1 tg 2
2
2
1
dx 2
dt
2
1 t

21. Пример

dx
8 4 sin x 7 cos x
dx
x
8tg
2
x
1 tg
2
8
7
2 x
2 x
1 tg
1 tg
2
2
2
2
dt
dt
1
t
dt 2 2
2
2
8t
7(1 t )
t 8t 15
(t 5)(t 3)
8
2
1 t
1 t 2
1
1
1
1
2
2
2 (
)dt (
)dt ln t 5 ln t 3 c
t 5 t 3
t 5 t 3
x
tg 5
t 5
2
ln
c ln
c
x
t 3
tg 3
2
2

22. Интегрирование тригонометрических функций

ПОДСТАНОВКА
Интегралы вида
t tgx.
R(tgx )dx
могут быть
рационализированы подстановкой t tgx.
Интегралы вида
R sin x, cos x dx,
где R sin x , cos x R sin x , cos x также
вычисляются подстановкой t tgx. или t ctgx.
2
t
1
2
2
t tgx , (cos x
, sin x
)
2
2
1 t
1 t

23. Интегрирование тригонометрических функций

R(sin
x, cos x ) dx
t cos x
R(sin x, cos x) R(sin x, cos x) t sin x
R( sin x, cos x) R(sin x, cos x)
sin x t
cos 3 x
1 sin 2 x
sin 4 x dx sin 4 x d sin x cos xdx dt
5
3
1 1
t
t
1
1
( 4 2 )dt
c 5 3 c
t
t
5 3
5t
3t
1
1
c
5
3
5 sin x 3 sin x

24. Интегрирование тригонометрических функций

sin
а) Если
m
n
x cos xdx.
m или n - целое положительное нечётное число,
то производится "расщепление" нечётной степени. Например,
2
3
sin
x
cos
xdx.
Если
m и n
целые положительные чётные числа, то
используются формулы понижения порядка
1 cos 2 x
1 cos 2 x
sin 2 x
2
cos x
, sin x
, sin x cos x
2
2
2
2

25. Интегрирование тригонометрических функций

sin
x
cos
xdx
Интегралы такого вида вычисляются путём
преобразования произведений в сумму с
помощью тригонометрических формул:
1
sin cos (sin( ) sin( ));
2
1
cos cos (cos( ) cos( ));
2
1
sin sin (cos( ) cos( )).
2

26. Определенный интеграл

Пусть функция y =f(x) определена на отрезке
[a,b], где a<b
1. Разобьем отрезок [a,b] точками x0=a<x1< x2<…<xn-1<
<xn=b на n частичных отрезков [x0, x1], [x1, x2],…, [xn-1, xn].
2. На каждом частичном отрезке [xi-1, xi] i 1, n выберем
произвольную точку сi xi 1 , xi и вычислим значение функции
f(ci) в этой точке i 1, n
3. Обозначим xi xi xi 1 и вычислим произведение
f (ci ) xi , i 1, n
с1
a x0 x1
с2
x2
.....
сn
xn 1 b xn

27. Определенный интеграл

4. Составим сумму Sn всех таких произведений,
то есть
n
S n f (c1 ) x1 f (c2 ) x2 ... f (cn ) xn
f (ci ) xi (1)
i 1
Сумма Sn вида (1) называется интегральной суммой
функции y=f(x) на отрезке [a,b]
Обозначим через max xi - максимальную длину
1 i n
отрезка разбиения.
5. Найдем предел интегральной суммы Sn при
что 0
n так,

28.

Определенный интеграл
Если предел интегральной суммы Sn при n так,
что 0 существует, конечен и не зависит от способа
разбиения отрезка [a,b] и способа выбора точек c1, c2,
… cn,то этот предел называется определенным
интегралом от функции
y=f(x) на отрезке [a,b] и
b
обозначается
f ( x)dx
a
знак интеграла
f ( x ) подынтегральная функция
f ( x ) dx подынтегральное выражение
a, b нижний и верхний предел интегрирования
[ a, b] область интегрирования

29. Определенный интеграл

b
a
f ( x ) dx lim
n
f (c ) x
n
( 0 ) i 1
i
i
(2)
Функция y=f(x), для которой существует предел
вида (2) называется интегрируемой на отрезке [a,b]

30. Свойства определенного интеграла, вытекающие из определения

Определенный интеграл не зависит от
переменной интегрирования, т.е.
1. обозначения
b
b
b
f ( x)dx f (t )dt f ( z )dz
a
2.
a
a
Определенный интеграл с одинаковыми
пределами интегрирования равен нулю, т.е.
a
f ( x)dx 0
a
b
3.
Для c R
cdx c (b a)
a

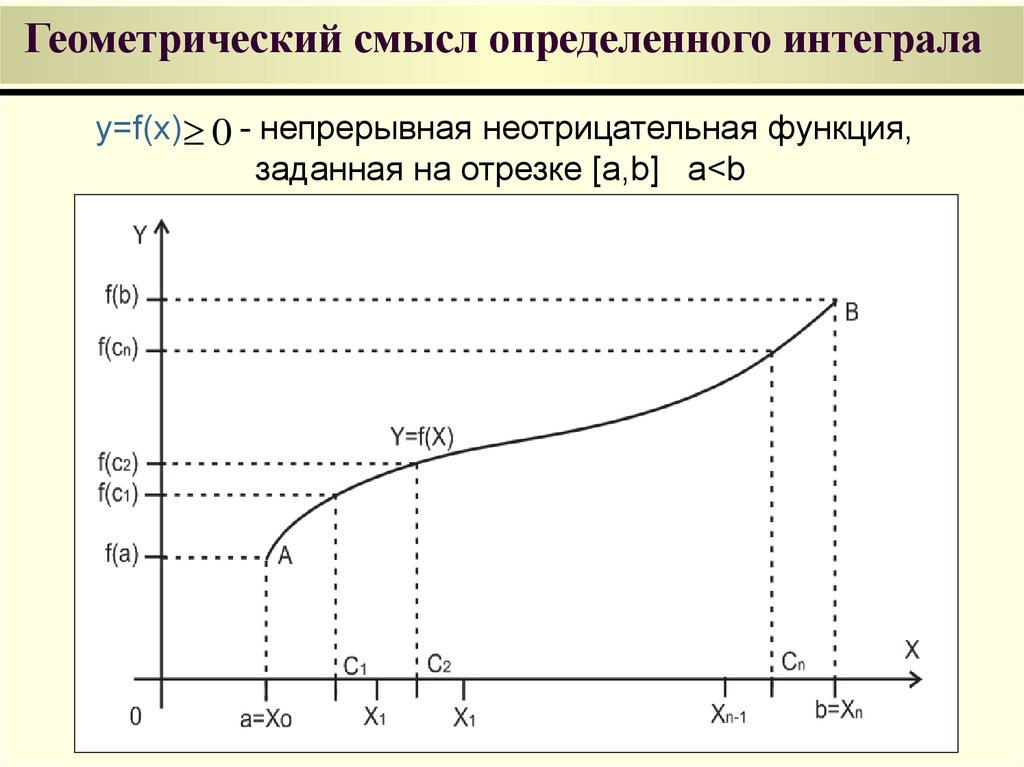
31. Геометрический смысл определенного интеграла

y=f(x) 0 - непрерывная неотрицательная функция,
заданная на отрезке [a,b] a<b

32. Геометрический смысл определенного интеграла

Фигура, ограниченная сверху графиком функции y =f(x),
снизу осью OX, сбоку прямыми x=a и x=b называется
криволинейной трапецией.
1. Разобьем отрезок [a,b] точками x0=a<x1< x2<…<xn-1<
<xn=b на n частичных отрезков [x0, x1], [x1, x2],…, [xn-1, xn].
2. На каждом частичном отрезке [xi-1, xi] i 1, n выберем
произвольную точку сi xi 1 , xi и вычислим значение функции
f(ci) для всех i 1, n
3. Обозначим xi xi xi 1 и рассмотрим f (ci ) xi - площадь
прямоугольника с высотой f (ci ) и длиной основания xi , где
i 1, n
4. Сумма произведений площадей таких прямоугольников
n
f (c1 ) x1 f (c2 ) x2 ... f (cn ) xn f (ci ) xi
i 1
равна площади ступенчатой фигуры и приближенно
равна
площади криволинейной трапеции

33. Геометрический смысл определенного интеграла

n
S f (ci ) xi - площадь криволинейной трапеции
i 1
Обозначим через max xi - максимальную длину
1 i n
отрезка разбиения.
5. С уменьшением точность приближения криволинейной
трапеции ступенчатой фигурой увеличивается, то есть
n
S n f (ci ) xi S при n так, что 0
i 1
S lim S n lim
n
( 0 )
b
n
f (c ) x f ( x)dx
n
( 0 ) i 1
i
i
a
Определенный интеграл от неотрицательной
непрерывной функции численно равен площади
криволинейной трапеции.

34. Формула Ньютона-Лейбница

Если функция y=f(x) непрерывна на отрезке [a,b] и F(x) –
-какая-либо ее первообразная на отрезке [a,b], то имеет
место формула
Ньютона-Лейбница
b
b
f ( x)dx F (b) F (a) F ( x) a
a

35. Пример

2
1
2 4 x 2 dx
2
1
1
x
2 4 x 2 dx 2 arctg 2
1
( )
2 4 4
4
2
2
1
(arctg1 arctg ( 1))
2

36. Основные свойства определенного интеграла

Свойство 1
Если с – постоянное число и функция f(x)
интегрируема на отрезке [a,b], то
b
b
cf ( x)dx c
a
f ( x)dx
a
Свойство 2
Если функции f1(x) и f2(x) интегрируемы на отрезке
[a,b], то интегрируема на этом отрезке их сумма
b
( f
1
a
b
( x) f 2 ( x)) dx
a
b
f1 ( x)dx f 2 ( x)dx
a
Это свойство распространяется на сумму любого
конечного числа слагаемых

37. Основные свойства определенного интеграла

Свойство 3
b
a
f ( x)dx f ( x)dx
a
b
Свойство 4
Если функция f(x) интегрируема на отрезке [a,b]
и a<c<b, то
с
b
a
f ( x)dx
a
b
f ( x)dx f ( x)dx
с

38. Основные свойства определенного интеграла

Свойство 5
(теорема о среднем)
Если функция f(x) непрерывна на отрезке [a,b]
, то с a, b , что
b
f ( x)dx f (c) (b a)
a
Свойство 6
Если функция f(x) сохраняет знак на отрезке [a,b],
b
где a<b, то
f ( x)dx имеет тот же знак, что и
a
f ( x ) 0 для
функция f(x), то есть если
b
x a, b , то f ( x)dx 0
a

39. Основные свойства определенного интеграла

Свойство 7
Неравенство между непрерывными на отрезке [a,b]
функциями можно интегрировать
Если f1 ( x) f 2 ( x), x a, b , то
b
a
b
f1 ( x)dx
a
f 2 ( x)dx

40. Основные свойства определенного интеграла

Свойство 8
(Оценка интеграла)
Если m и M соответствующее наименьшее и
наибольшее значение функции f(x) на отрезке [a,b]
(a<b), то есть m f ( x) M для x a, b ,то
b
b
mdx
a
m(b a)
a
b
a
b
f ( x)dx
Mdx
a
f ( x)dx M (b a)

41. Основные свойства определенного интеграла

Свойство 9
Производная определенного интеграла с
переменным верхнем пределом по этому пределу
равна подынтегральной
функции для этого предела,
x
то есть ( f (t )dt ) f ( x)
x
a

42. Интегрирование методом замены переменной

Если: 1) функция x (t ) и ее производная x (t )
непрерывны при t ,
2) множеством значений функции x (t )при
t , является отрезок [a,b]
3) ( ) a, ( ) b
b
Тогда
f ( x)dx f ( (t )) (t )dt
(1)
a
1. При вычислении определенного интеграла
методом замены переменной возвращаться к
старой переменной не надо.
2.Необходимо менять пределы интегрирования
при замене переменной.

43. Пример

2
2
x
4 x 2 dx
1
x 2 sin t x 2 4 sin 2 t
dx 2 cos tdt
2
2
2
x
4
x
dx
0
2
2
x 0 2 sin t 0 t 0
x 2 2 sin t 2 t
2
2
2
4 sin 2 t 4 cos 2 tdt
0
2
2
1 cos 4t
1 cos 4t
1
4 sin 2tdt 4
dt 4 (
)dt 2 dt cos 4td 4t
2
2
2
20
0
0
0
0
2
1
2t 2 sin 4t 2
0 2
0

44. Метод интегрирования по частям

Если функции u=u(x); v=v(x) имеют непрерывные
производные на отрезке [a,b], то справедлива
формула интегрирования по частям
b
b
b
(5)
udv uv a vdu
a
a

45. Пример

e
x
ln
xdx
2
1
1
u ln x du dx
e
e
e 1 2
1 3
2
x
x ln x x dx
3
0 x ln xdx
x
1 31
3
2
dv x dx v
3
3
1 3 1 x e 1 3 1 3 1 2 3 1
e
e e e
3
3 3 1 3
9
9 9
9

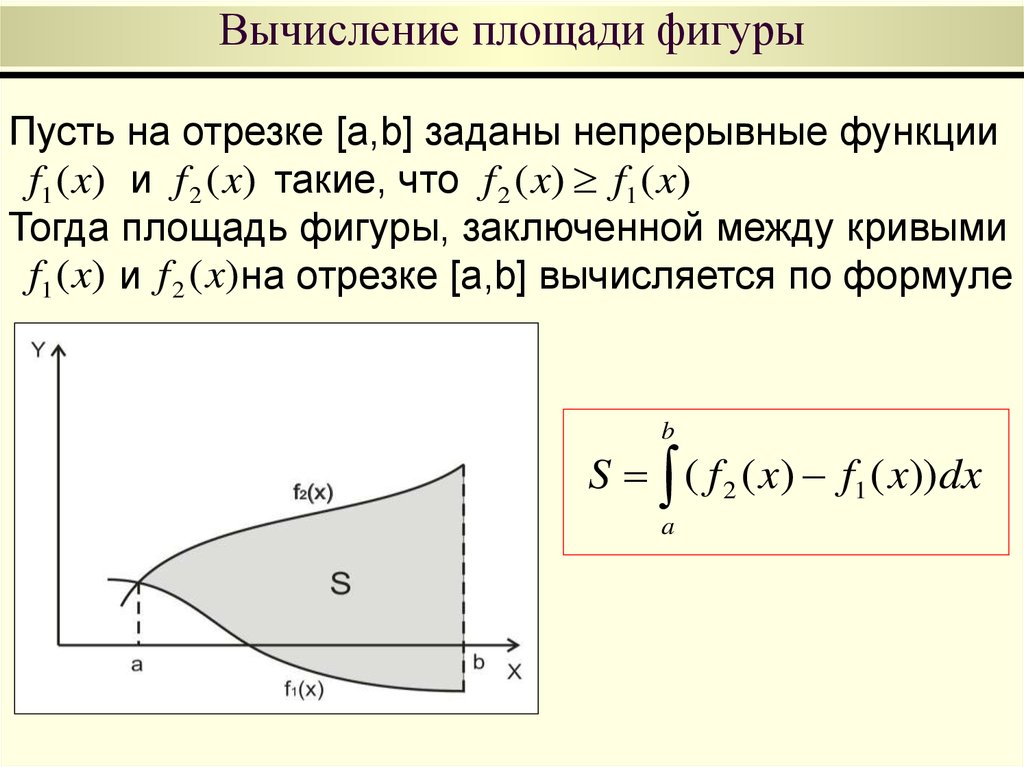
46. Вычисление площади фигуры

Пусть на отрезке [a,b] заданы непрерывные функции
f1 ( x) и f 2 ( x) такие, что f 2 ( x) f1 ( x)
Тогда площадь фигуры, заключенной между кривыми
f1 ( x) и f 2 ( x) на отрезке [a,b] вычисляется по формуле
b
S ( f 2 ( x) f1 ( x)) dx
a

47. Вычисление площади фигуры

f 2 ( x) f1 ( x) 0
1.
y f 2 ( x)
y f1 ( x)
a
b
b
b
b
a
a
a
S SaA2 B2b SaA1B1b f 2 ( x)dx f1 ( x)dx ( f 2 ( x) f1 ( x))dx

48. Вычисление площади фигуры

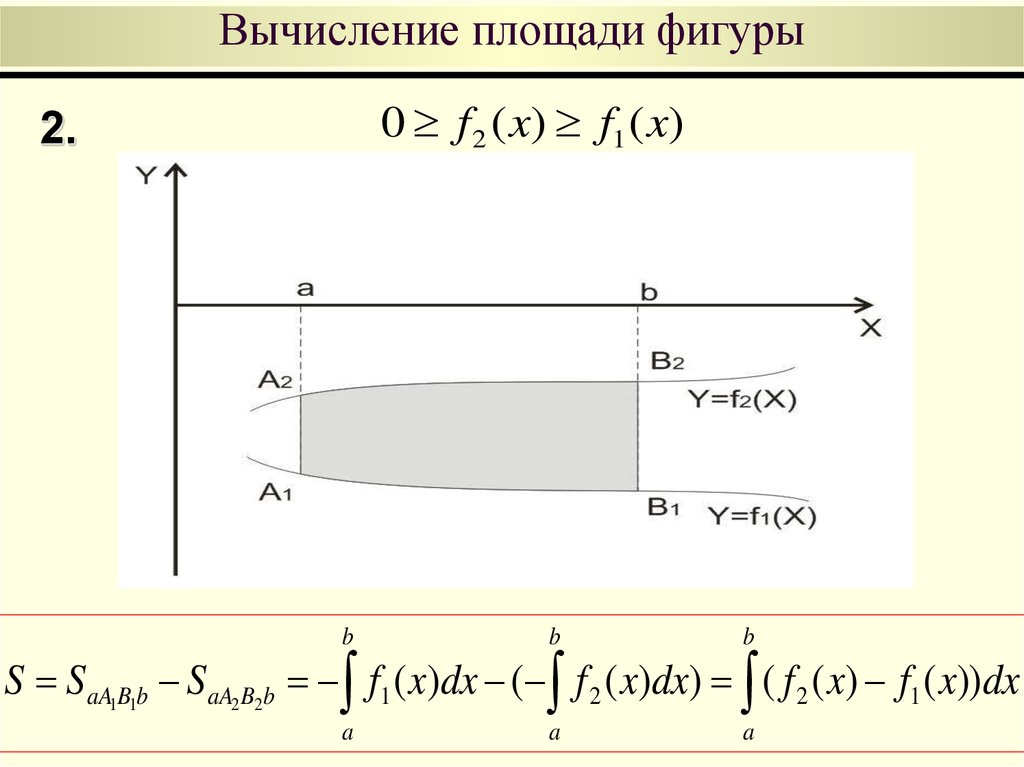
0 f 2 ( x) f1 ( x)
2.
b
b
b
a
a
a
S SaA1B1b SaA2 B2b f1 ( x)dx ( f 2 ( x)dx) ( f 2 ( x) f1 ( x))dx

49. Вычисление площади фигуры

3.
f 2 ( x) f1 ( x), f 2 ( x) 0, f1 ( x) 0
b
b
b
a
a
a
S SaA2 B2b SaA1B1b f 2 ( x)dx ( f1 ( x)dx) ( f 2 ( x) f1 ( x))dx

50. Вычисление площади фигуры

4.
Сводится к случаем 1, 2, 3 путем разбиения отрезка
[a,b] на отдельные отрезки [a,c], [c,d], [d,b]

51. Пример

Найти площадь фигуры, ограниченной линиями
y x 2 и параболой y 4 x
2
2
S (4 x x 2)dx
2
3
2
(6 x x)dx
2
3
x 2 x3 2
5
(6 x )
20
2 3 3
6
5 2
S 20 ед
6

52. Вычисление объема тела вращения

Пусть функция y=f(x) непрерывна и неотрицательна
на отрезке [a,b].
Тогда тело, которое образуется при вращении вокруг
оси OX криволинейной трапеции aABb, имеет объем:
b
Vx f ( x)dx
2
a

53. Вычисление объема тела вращения

b
Vx f 2 ( x)dx
a
1. Разобьем отрезок [a,b] точками x0=a<x1< x2<…<xn-1<
<xn=b на n частичных отрезков [x0, x1], [x1, x2],…, [xn-1, xn].
2. На каждом частичном отрезке [xi-1, xi] i 1, n построим
прямоугольник MPQN. Выберем произвольную точку сi xi 1 , xi
i 1, n
3. При вращении вокруг оси ОХ прямоугольник MPQN опишет
цилиндр, объем которого будет равен f 2 (ci ) xi , где
xi xi nxi 1 - высота цилиндра, f (ci ) - радиус основания
4. Сумма f 2 (c ) x является приближением для искомого
i 1
объема
i
Vx lim
max xi 0
i
i
n
b
i 1
a
2
2
f
(
c
)
x
f
i
i
( x)dx

54. Вычисление объема тела вращения

55. Вычисление объема тела вращения

Пусть функция y=f(x) непрерывна и неотрицательна
на отрезке [a,b].
Тогда тело, которое образуется при вращении вокруг
оси OY криволинейной трапеции, имеет объем:
d
Vy ( y)dy
2
c

56. Пример

Найти объем тела, образованного вращением вокруг
оси ОY фигуры, ограниченной линиями
2
x
y , x 0, y 2 2
2
Vy
2 2
2 ydy
0
y
2
2 2
0
8
Vy 8 (ед )
3

57. Несобственные интегралы

Несобственные интегралы
определенные интегралы
от непрерывной функции, с
бесконечным промежутком
интегрирования
определенные интегралы
с конечным промежутком
интегрирования, но для
функции, имеющей на
нем бесконечный разрыв

58. Несобственные интегралы первого рода

Пусть функция y=f(x) непрерывна на промежутке
[ a, ) . Если существует конечный предел вида
b
lim
b
f ( x)dx
, то его называют несобственным
a
интегралом первого рода и обозначают
f ( x)dx
a
b
lim
b
f ( x)dx
a
Если существует конечный предел, то говорят, что
несобственный интеграл сходится, в противном
случае (не существует или бесконечен) - расходится

59. Несобственные интегралы первого рода

f ( x)dx
a
b
lim
b
f ( x)dx
a
Если непрерывная функция f ( x ) 0 на промежутке
[ a, ) и интеграл
f ( x)dx сходится, то он выражает
a
площадь бесконечно длинной криволинейной трапеции

60. Несобственные интегралы первого рода

Несобственный интеграл на промежутке ( , b]
b
f ( x)dx
b
lim
a
f ( x)dx
a
Несобственный интеграл с двумя бесконечными
пределами
с
с
f ( x)dx f ( x)dx f ( x)dx
С – произвольное число

61. Примеры

b
dx
1b
1
2
x dx lim
lim ( 1) 1
1 x 2 blim
b x 1
b b
1
интеграл сходится
0
0
0
cos xdx lim cos xdx lim sin x a lim (0 sin a)
a
a
a
a
lim sin a - не существует – интеграл расходится
a

62. Несобственные интегралы второго рода

Пусть функция y=f(x) непрерывна на промежутке
[a, b) и имеет бесконечный разрыв при x=b. Если
существует конечный предел
вида
b
lim
0
f ( x)dx
a
то его называют несобственным интегралом второго
рода и обозначают
b
b
f ( x)dx
f ( x)dx lim
a
0
a
Если существует конечный предел, то говорят, что
несобственный интеграл сходится, в противном случае (не
существует или бесконечен) - расходится

63. Несобственные интегралы первого рода

b
b
f ( x)dx
f ( x)dx lim
a
0
a
Если функция f(x)>0 на промежутке [a,b] и интеграл
b
f ( x)dx
сходится, то он выражает
a
площадь бесконечно высокой криволинейной трапеции

64. Несобственные интегралы второго рода

Функция y=f(x) терпит бесконечный разрыв в
точке x=a
b
b
f ( x)dx
f ( x)dx lim
0
a
a
Функция y=f(x) терпит разрыв во внутренней
точке с отрезка [a,b]
b
с
b
a
a
с
f ( x)dx f ( x)dx f ( x)dx

65. Пример

1
0
1
0
1
1
2
dx
x
1
2
1
dx
lim x dx lim 2 x
lim 2(1 ) 2
0
0
x 0