Similar presentations:
Интегральное исчисление. Приложения определённого интеграла
1. Интегральное исчисление
Приложенияопределённого
интеграла
2. Студент должен знать
понятиянеопределённого и
определённого интегралов;
свойства интегралов;
таблицу неопределённых интегралов;
методы интегрирования;
формулу Ньютона-Лейбница.
3. Заполните таблицу
F(x)f(x)=F′(x)
F ( x ) x 11
f ( x) 3x
3
2
F (x) x 0,2 f ( x ) 2 x
4
3
x
F (x)
f ( x) 4 x
2
2
4. Первообразная (определение)
y = F(x), y = f(x), D(F) = D(f) = X,F(x) – первообразная для f(x),
если для всех x Х:
F (x) = f(x).
5. Определить первообразную функции f(x) = 3x2
Определить первообразную2
функции f(x) = 3x
F(x) = x3
т.к.
F (x) = (x3) = 3x2 = f(x).
6. Определить первообразную функции f(x) = 3x2
Определить первообразную2
функции f(x) = 3x
1. F(x) = x3+1, т.к.
F (x) = (x3+1) = 3x2+0 = f(x).
F(x) = x3–7, т.к.
F (x) = (x3–7) = 3x2–0 = f(x).
2.
7. Теорема 1
Функция f(x), имеетбесконечное множество
первообразных вида F(x)+С.
8. Неопределённый интеграл
f ( x)dx F ( x) Cf(x) – подынтегральная функция,
f(x)dx – подынтегральное выражение.
9. Свойства неопределённого интеграла
10. Теорема 2
d f ( x)dx f ( x)dxДифференциал
интеграла функции
равен подынтегральному выражению.
11. Теорема 3
f ( x)dxПроизводная
f ( x)
интеграла равна
подынтегральной функции.
12. Теорема 4
f ( x)dx f ( x) CИнтеграл
производной функции равен
сумме этой функции с произвольной
константой.
13. Теорема 5
fx
g
x
dx
f x dx g x dx
Интеграл суммы равен сумме интегралов
14. Теорема 6
kfx
dx
k
f
x
dx
Постоянный множитель выносится за знак
интеграла
15. Основные формулы интегрирования
16. Интеграл дифференциала аргумента
dxx
C
17. Интеграл степенной функции
n 1x
x
dx
C
,
n 1
n 1
n
18. Интеграл обратной пропорциональности
dxln
x
C
,
x
x 0
19. Интеграл экспоненциальной функции
edx
e
C
x
x
20. Интеграл показательной функции
xx
a
a
dx
C
ln a
21. Интеграл функции косинуса
cosxdx
sin
x
C
22. Интеграл функции синуса
sinxdx
cos
x
C
23. Методы интегрирования
1.2.
3.
Непосредственное
интегрирование
Метод подстановки (замены
переменной)
Метод интегрирования по частям
24. Непосредственное интегрирование
Найти:2 x
3
3 x 2 x 8 dx
2
25.
2x3
3 x 2 x 8 dx
2
2 x dx 3 x dx 2 xdx 8dx
3
2
2 x dx 3 x dx 2 xdx 8 dx
3
2
x x x
3
2
8 x C
2
3 1 2 1 1 1
3 1
2 1
4
1 1
x
3
2
x x 8 x C.
2
26. Метод подстановки (замены переменной)
Найти:x
3
4
3 x dx
2
27. Введение подстановки
t x 33
2
dt d x 3 x 3 dx 3 x dx
3
3
dt 3 x dx
2
1
x dx dt
3
2
28.
1x 3 x dx t dt
3
5
1 4
1 t
t dt C
3
3 5
4
3
4
2
t
x 3
C
C.
15
15
5
3
5
29. Метод интегрирования по частям
udu
du
30. Найти:
xln
xdx
Чтобы воспользоваться формулой
ud u du
необходимо выбрать функцию u и дифференциал dυ
Пусть u = x и dυ = lnx.
Тогда: du = dx и
d ln xdx
Такой выбор неудачен: невозможно интегрирование.
31.
Выберем функцию u и дифференциал dυ иначе:Пусть u = lnx и dυ = xdx.
2
и
x
xdx
2
32. Образец оформления
dxu ln x; du
x
x
ln
xdx
2
x
d xdx;
2
2
2
2
x
x dx x
xdx
ln x
ln x
2
2x
2
2
33.
22
2
x
1 x
x
1
ln x xdx ln x C
2
2 2
2
2
2
2
2
x
1
x
x
ln x C ln x C
2
2
2
4
2
x
2 ln x 1 C.
4
34. Определённый интеграл
Определённыйинтеграл функции
y=f(x) есть число, значение которого
зависит от вида этой функции и пределов
интегрирования a и b:
b
a
f x dx
35. Определённый интеграл
bf x dx
a
f(x) – подынтегральная функция,
f(x)dx – подынтегральное выражение,
a – нижний предел интегрирования
b – верхний предел интегрирования
36. Формула Ньютона-Лейбница
bb
a
f x dx F b F a
a
f x dx F x a F b F a .
b
37. Свойства определённого интеграла
38. Теорема 7 (аддитивность)
a c bb
a
c
b
a
c
f ( x)dx f ( x)dx f ( x)dx
39. Теорема 8
bf
x
g
x
dx
a
b
b
a
a
f x dx g x dx
40. Теорема 9
bb
a
a
kf
x
dx
k
f
x
dx
41. Теорема 10
ba
a
f x dx f x dx
b
42. Вычисление определённых интегралов
Вычислить:3
x
dx
.
3
1
43.
Вычисление определённыхинтегралов
3
4 3
x
x
dx
1
4
3
1
3
4
4
1
4
81 1 80
20.
4 4 4
4
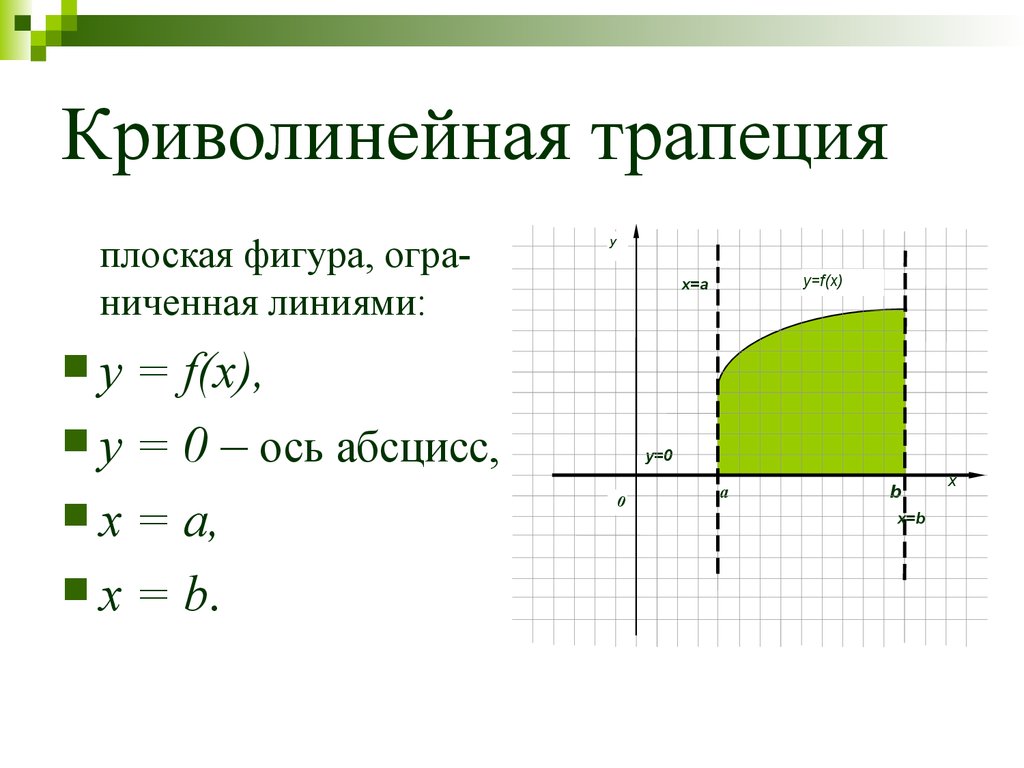
44. Криволинейная трапеция
плоская фигура, ограниченная линиями:= f(x),
y = 0 – ось абсцисс,
x = a,
x = b.
y
y=f(x)
x=a
y
y=0
0
a
b
x=b
x
45. Площадь криволинейной трапеции
bS f x dx.
a
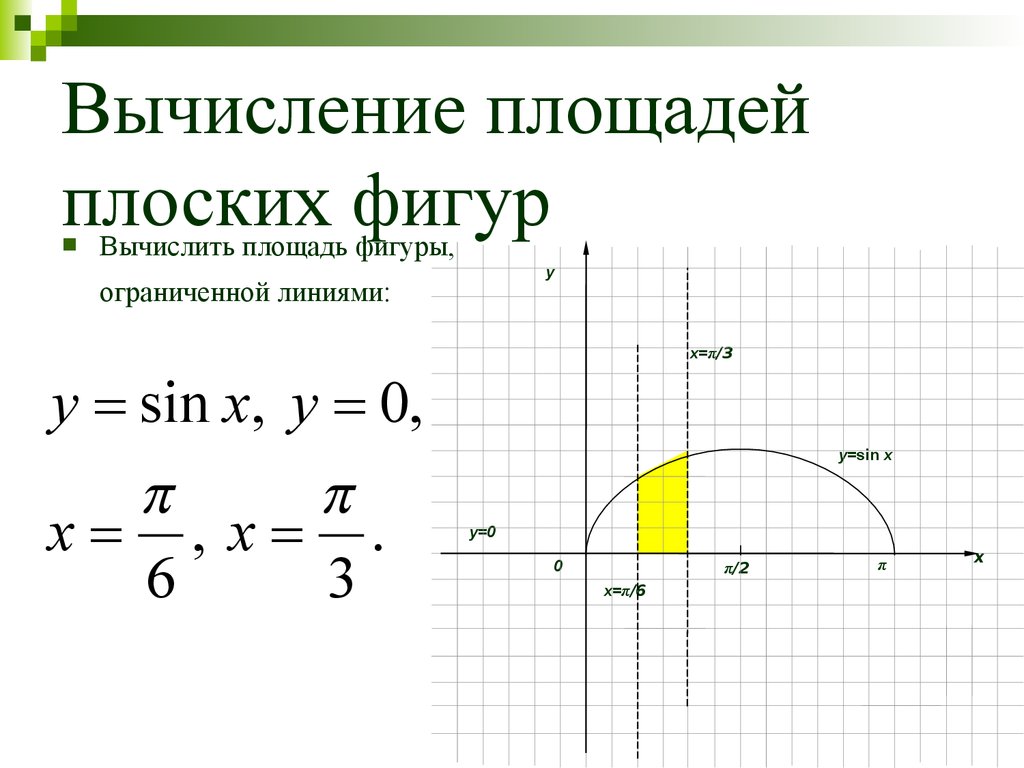
46. Вычисление площадей плоских фигур
Вычислить площадь фигуры,y
ограниченной линиями:
x=π/3
y sin x, y 0,
x , x .
6
3
y=sin x
y=0
0
π/2
x=π/6
π
x
47.
3S
3
6
cos
x
sin
xdx
6
cos cos
3
6
1
3
2 2
1
3
3 1 (кв.ед.).
2 2
2
48. Дифференциальные уравнения
49. Дифференциальное уравнение* –
это уравнение, связывающеенезависимую
переменную x,
её функцию y,
производные различных порядков этой
функции: y’, y”, y’”…
*«Дифференциальное уравнение» будем кратко обозначать
аббревиатурой «ДУ»
50. Решить ДУ –
это значит, найти множество всехфункций, которые удовлетворяют
данному ДУ:
Такое
множество функций имеет вид:
y = f(x; C), где C – произвольная
постоянная,
Это
– общее решение ДУ.
51. Обыкновенное ДУ* –
это ДУ, которое имеет только однунезависимую переменную (например, х или t).
ДУ в частных производных** – это ДУ, которое
имеет две и более независимых переменных.
*«Обыкновенное дифференциальное уравнение» будем кратко
обозначать аббревиатурой «ОДУ».
**Такие ДУ в рамках нашей программы не рассматриваются.
52. Порядок* ОДУ –
это порядок старшей производной:y’ + 1 = 0
– ОДУ первого порядка;
y” + y = x sinx
– ОДУ второго порядка;
y(V) + y(III) = a y, a R
– ОДУ пятого порядка.
*В рамках нашей программы будут рассматриваться только ОДУ первого
порядка.
53. Решение ОДУ
ОДУ: y’ = x2;Одно из решений: y = (1/3) x3;
Проверка:
((1/3) x3)’ =
(1/3) (x3)’ = (1/3) 3x2 = x2.
Другое решение ОДУ: y = (1/3) x3 + 1,2.
ОДУ могут иметь множество решений.
54. Общее решение ОДУ –
это множество решений, содержащее ВСЕбез исключения решения этого
дифференциального уравнения.
55. Частное решение ОДУ –
одно из множества решений ОДУ, удовлетворяющееизначально заданным дополнительным условиям:
ОДУ:
y’ = x2,
y(1) = 1;
Общее решение: y(x) = (1/3) x3 + С.
Найдём С:
1 = (1/3) 13 + С
С = 2/3.
Частное решение ОДУ: y = (1/3) x3 + 2/3.
56. Задача Коши –
это задача нахождения частного решениядифференциального уравнения,
удовлетворяющего заданным начальным
условиям.
57. ОДУ с разделяющимися переменными –
это уравнение, которое возможнопреобразовать таким образом, что правая
часть будет содержать выражения только с
переменной y, а левая – только с
переменной х (или наоборот).
58. Пример 1
Найти общее решение ОДУxy’ = y.
Решение ОДУ происходит в несколько
этапов:
59. Этап 1: расшифровка производной
Запишем:Тогда:
y’ = dy/dx
xy’ = y
x dy/dx = y;
60. Этап 2: разделение переменных
x dy/dx = y;По свойству пропорции, перенесём «крестнакрест» х и dx вправо, а y – влево:
dy/y = dх/x;
61. Этап 3: интегрирование
Найдём интегралы левой и правой частейуравнения:
(dy/y) = (dх/x);
ln y = ln x + константа;
константа = ln С ;
ln y = ln x + ln С ;
62. Этап 4: нахождение y в явном виде
Найдём общее решение (функцию y) в явном виде:ln y = ln x + ln С ;
ln y = ln Cx ;
y = Сx.
Ответ: y = Сx, где С – константа.
*Общее решение ОДУ – семейство функций (здесь – семейство прямых
пропорциональностей).
63. Пример 2 (задача Коши)
Найти частное решение дифференциальногоуравнения
y’ = –2y,
удовлетворяющее начальному условию
y(0) = 2.
64. Этап 1: расшифровка производной
Запишем:Тогда:
y’ = dy/dx
y’ = –2y
dy/dx = –2y;
65. Этап 2: разделение переменных
dy/dx = –2y;По свойству пропорции, перенесём «крестнакрест» dx вправо, а y – влево:
dy/y = –2dх;
66. Этап 3: интегрирование
Найдём интегралы левой и правой частейуравнения:
dy/y = dх;
(dy/y) = (–2dх);
(dy/y) = –2 dх;
ln y = –2x + С`;
67. Этап 4: нахождение y в явном виде
Найдём общее решение (функцию y) в явном виде:ln y = –2x + С`;
Учтём: если lna = b, то a = eb;
y = e–2x + С`;
y = eС` e–2x
Переобозначим: eС` = С,
тогда общее решение будет иметь вид: y = Сe–2x.
(семейство экспоненциальных функций)
68. Этап 5: нахождение частного решения
Найдём частное решение для y(0) = 2:= 0: y = Сe–2 0 = Сe0 = С 1 = С = 2.
Тогда y = Сe–2x и С = 2
y = 2e–2x – частное решение ОДУ.
При х
Ответ:
y = 2e–2x.
69. Итоги
свойстваинтегралов;
таблица неопределённых интегралов;
методы интегрирования;
формула Ньютона-Лейбница;
дифференциальные уравнения;
задача Коши.
70. Домашнее задание
К практическому занятию №3:Теория
– лекционный материал;
Письменно – упражнения для
самостоятельной работы.















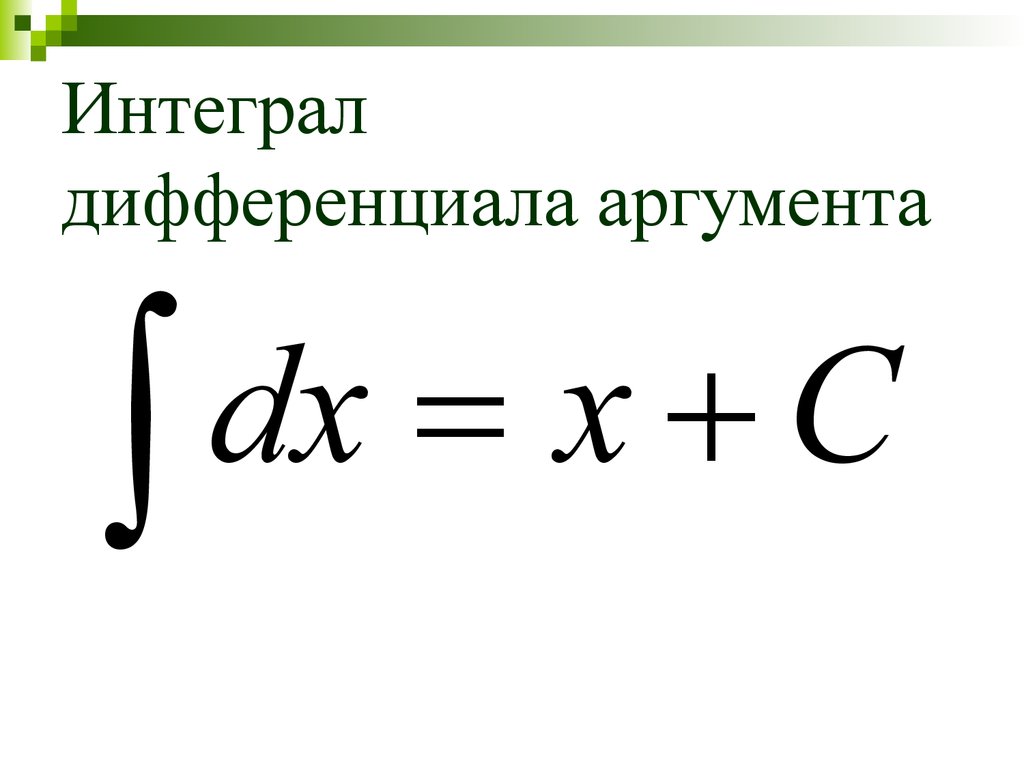


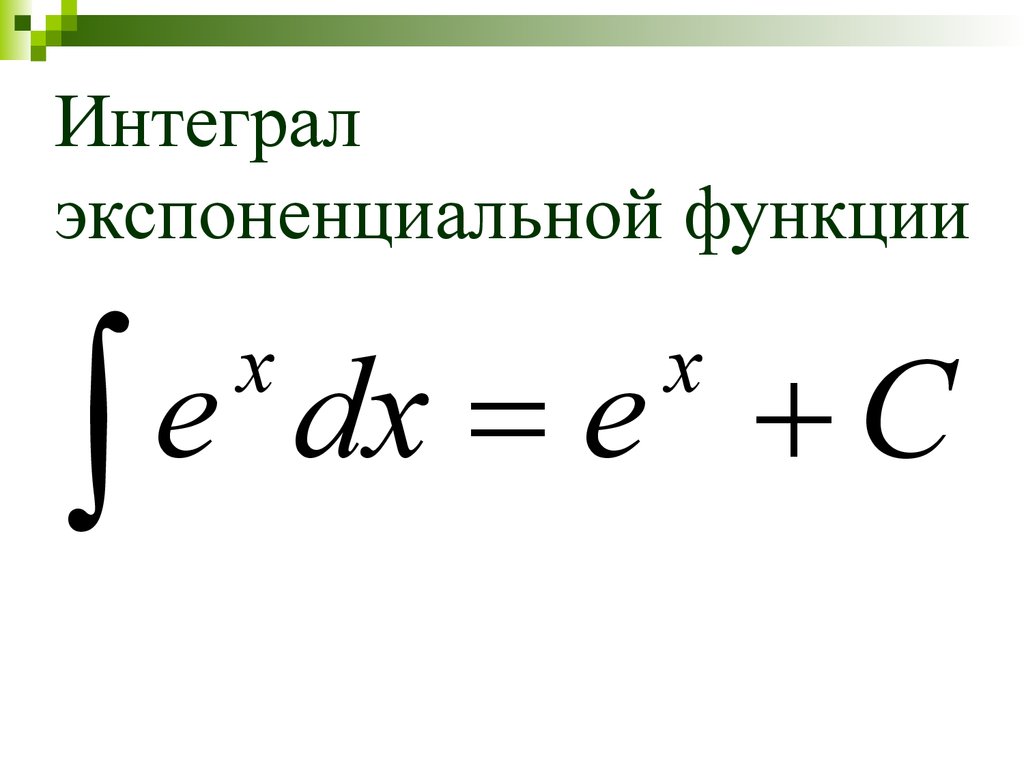
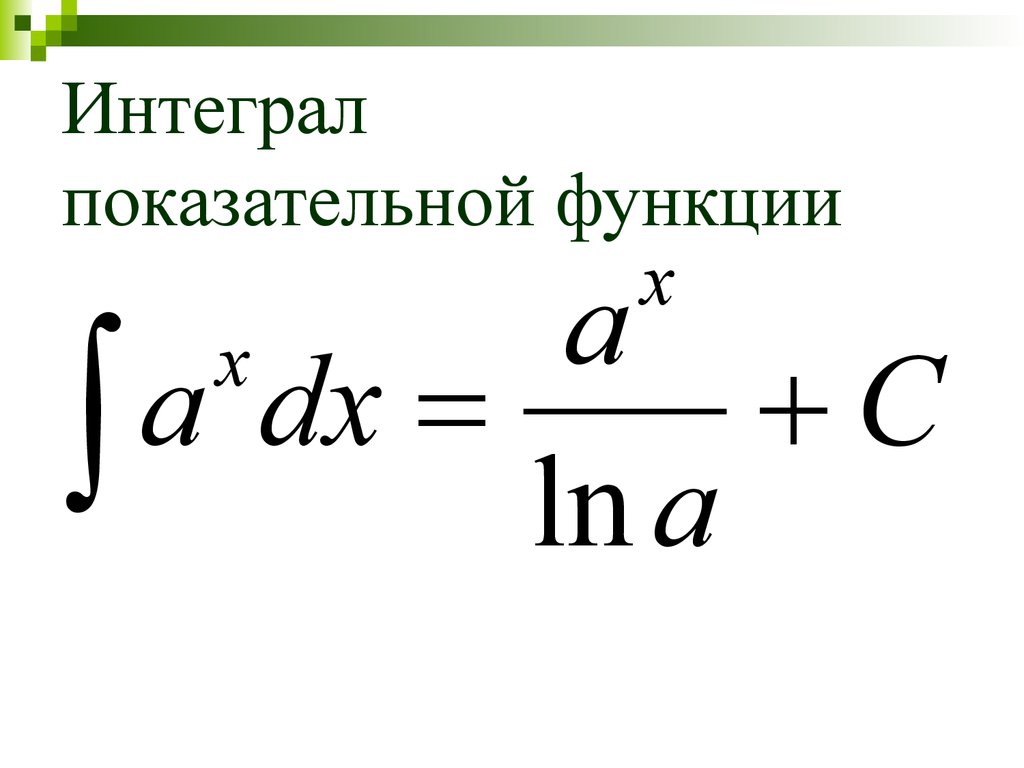




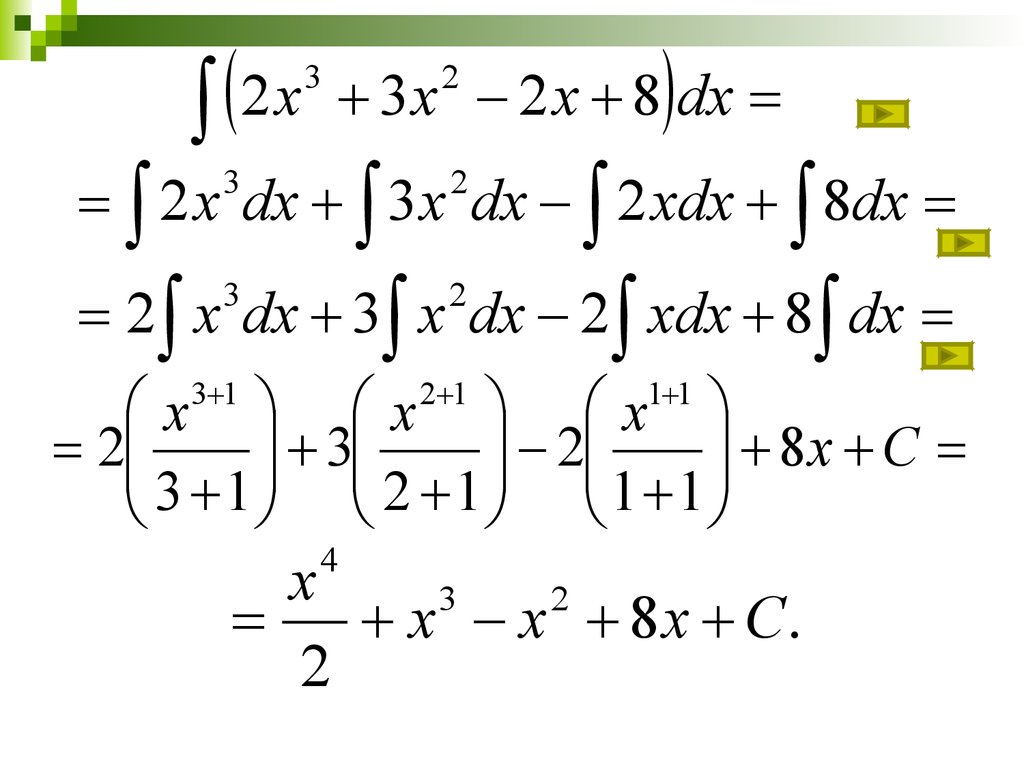


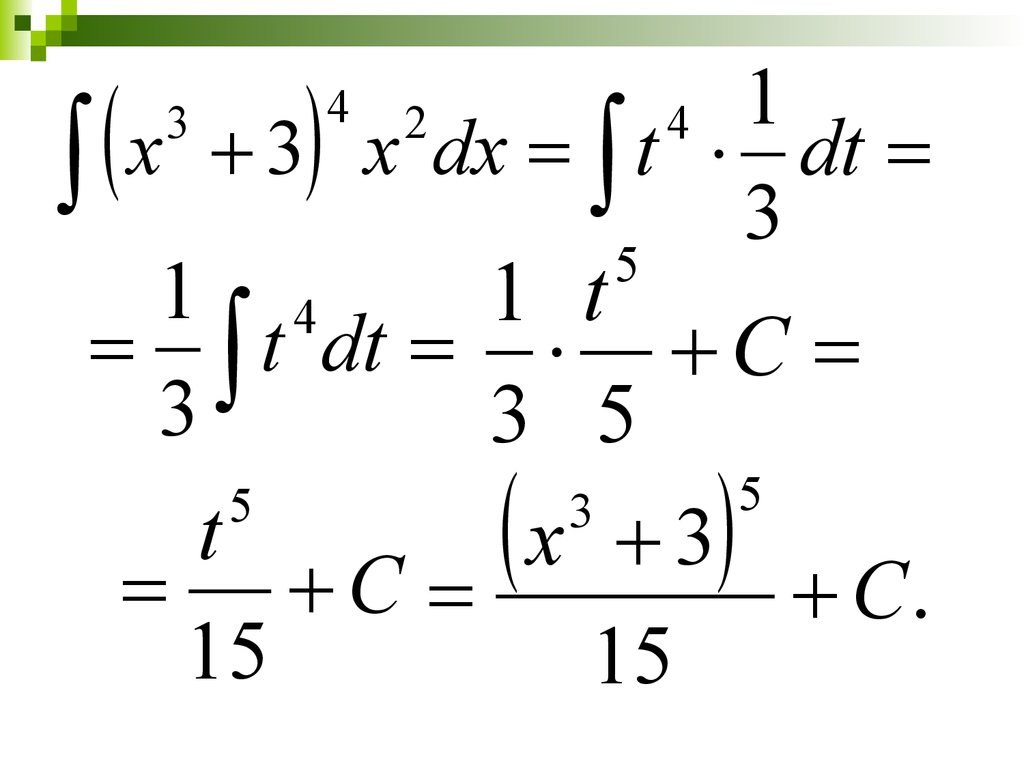
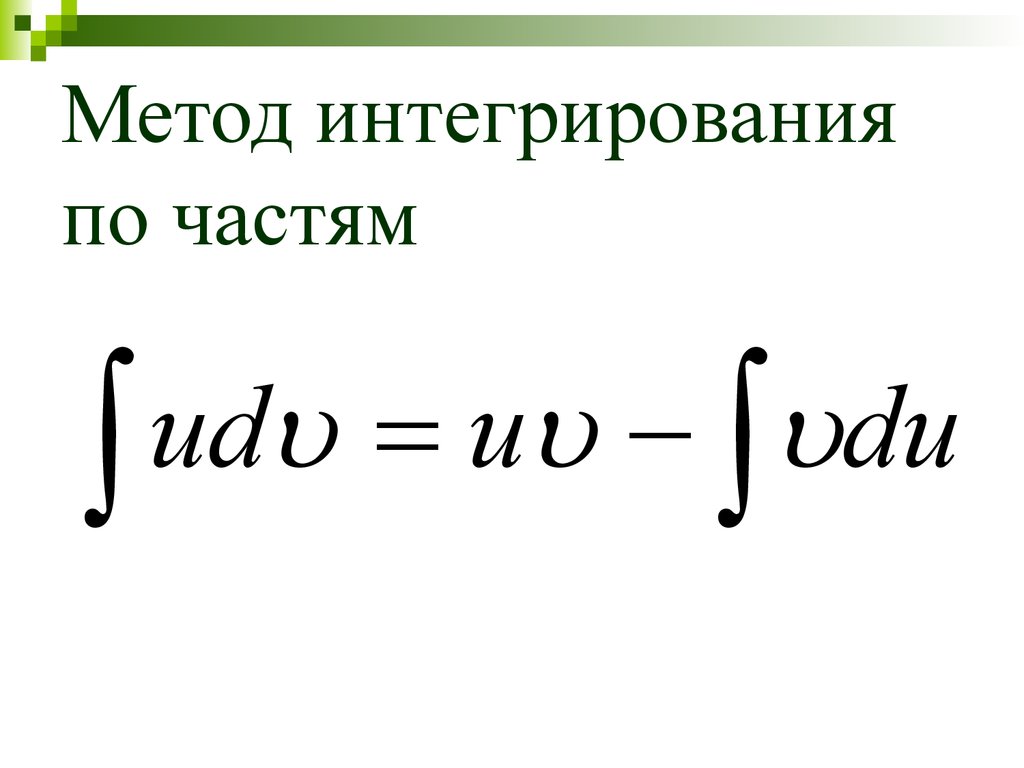

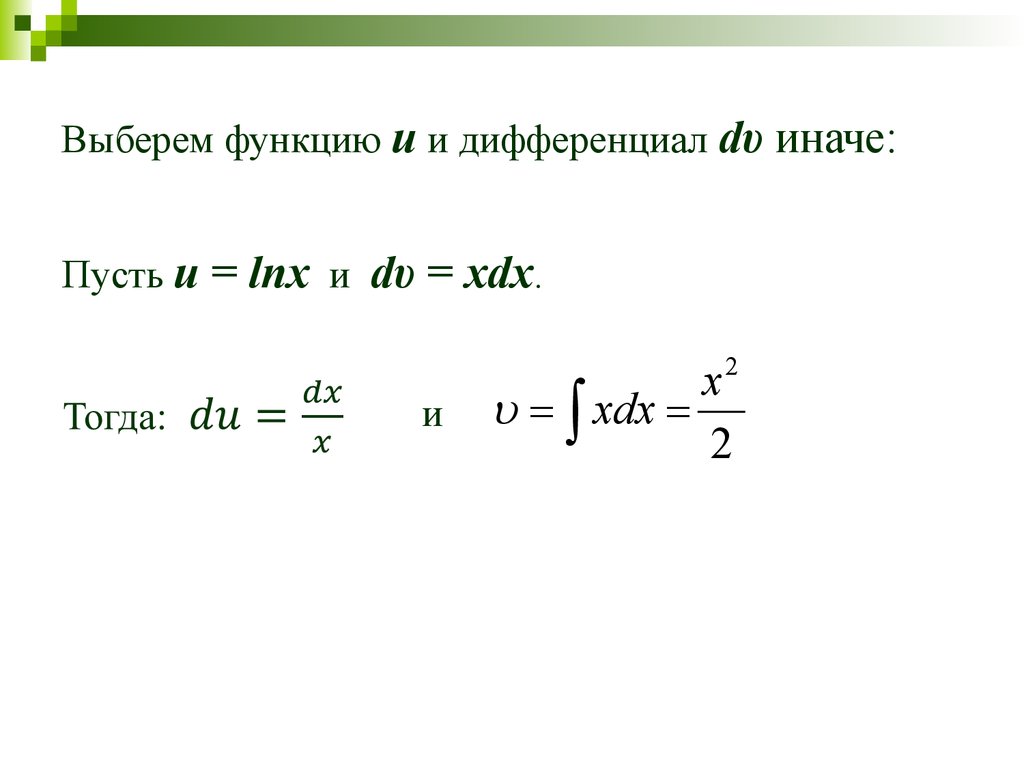












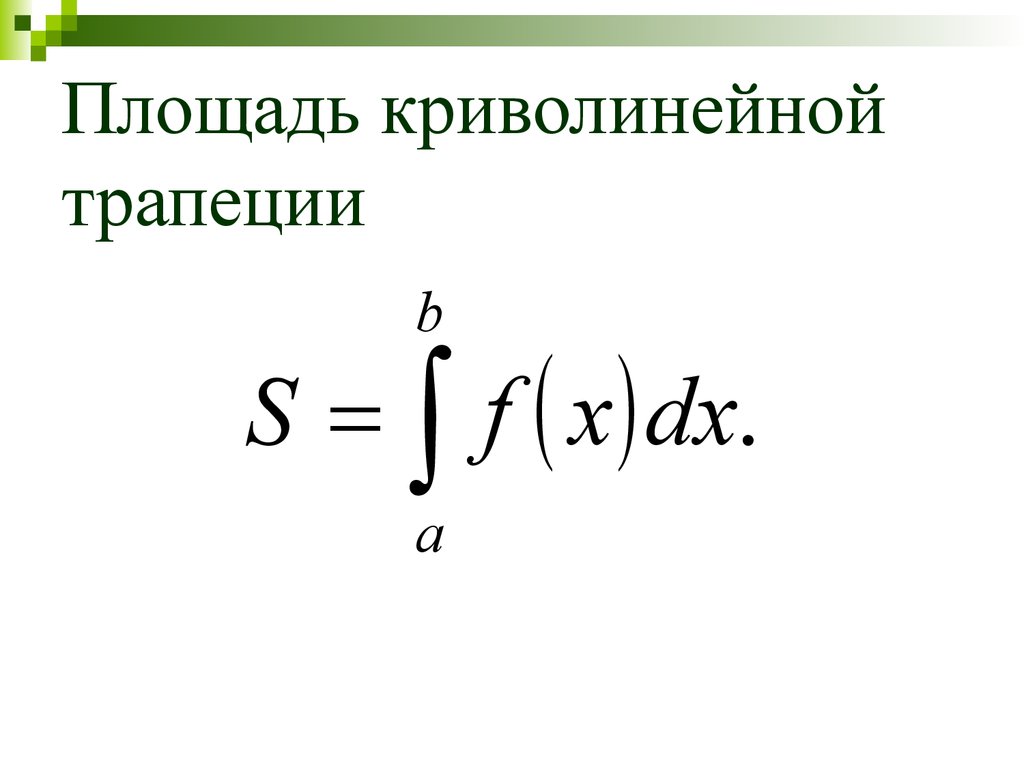
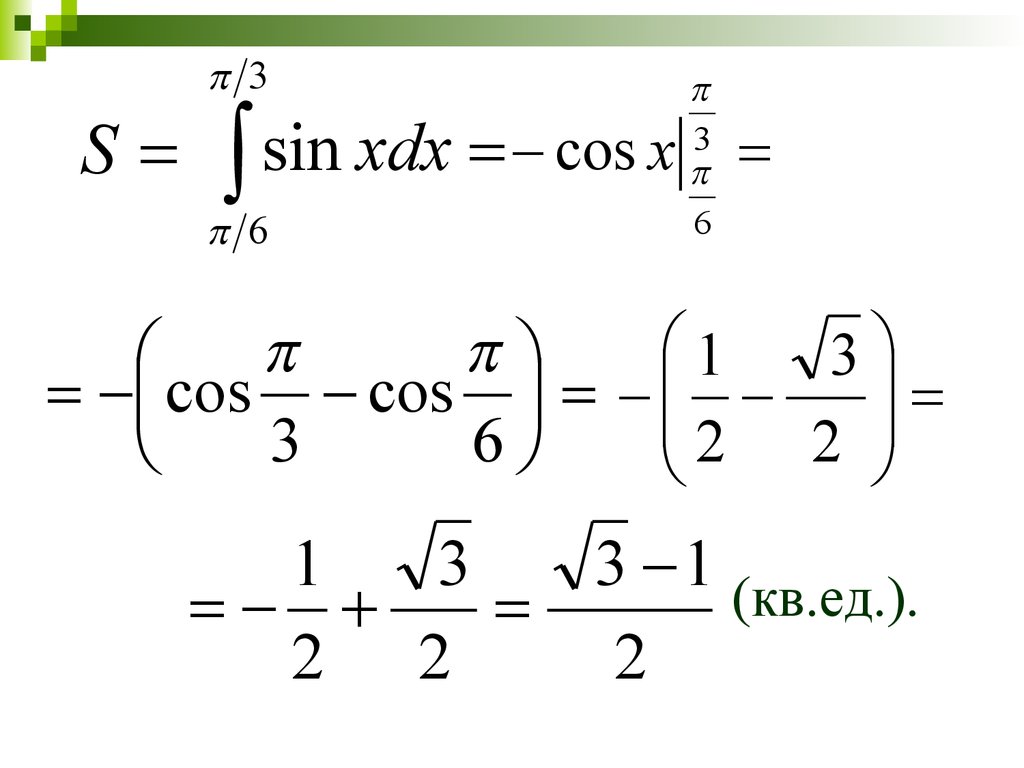
























 mathematics
mathematics








