Similar presentations:
Неопределенный интеграл, его свойства и вычисление. Первообразная и неопределенный интеграл
1. Прикладная математика каф. МЕН
Аношина О.В.2. Основная литература
• 1. Шипачев В. С. Высшая математика. Базовый курс: учебник ипрактикум для бакалавров [Гриф Минобразования РФ] / В. С.
Шипачев; под ред. А. Н. Тихонова. - 8-е изд., перераб. и доп. Москва : Юрайт, 2015. - 447 с.
• 2. Шипачев В. С. Высшая математика. Полный курс: учебник
для акад. бакалавриата [Гриф УМО] / В. С. Шипачев; под ред. А.
Н. Тихонова. - 4-е изд., испр. и доп. - Москва : Юрайт, 2015. - 608
с
• 3. Данко П.Е., Попов А.Г., Кожевникова Т..Я. Высшая математика
в упражнениях и задачах. [Текст] / П.Е. Данко, А.Г. Попов, Т.Я.
Кожевникова. В 2 ч. – М.: Высшая школа, 2007. – 304+415c.
3. Отчетность
1.Контрольная работа. Выполняется в соответствии:
Задания и методические указания к выполнению контрольных работ
по дисциплине «ПРИКЛАДНАЯ МАТЕМАТИКА», Екатеринбург, ФГАОУ
ВО «Российский государственный профессионально-педагогический
университет», 2016 - 30с.
Вариант контрольной работы выбирать по последней цифре номера
зачетной книжки.
2.
Экзамен
4. Неопределенный интеграл, его свойства и вычисление Первообразная и неопределенный интеграл
Определение. Функция F x называетсяпервообразной функции f x , определенной на
некотором промежутке, если F x f x для
каждого x из этого промежутка.
Например, функция cos x является
первообразной функции sin x , так как
cos x sin x .
5.
Очевидно, если F x - первообразнаяфункции f x , то F x C , где C некоторая постоянная, также является
первообразной функции f x .
Если F x есть какая-либо первообразная
функции f x , то всякая функция вида
Ф x F x C также является
первообразной функции f x и всякая
первообразная представима в таком виде.
6.
Определение. Совокупность всехпервообразных функции f x ,
определенных на некотором
промежутке, называется
неопределенным интегралом от
функции f x на этом промежутке и
обозначается f x dx .
7.
Если F x - некоторая первообразная функцииf x , то пишут f x dx F x C , хотя
правильнее бы писать f x dx F x C .
Мы по устоявшейся традиции будем писать
f x dx F x C .
Тем самым один и тот же символ
f x dx будет обозначать как всю
совокупность первообразных функции f x ,
так и любой элемент этого множества.
8. Свойства интеграла
Производная неопределенного интеграла равнаподынтегральной функции, а его дифференциалподынтегральному выражению. Действительно:
1.( f ( x)dx) ( F ( x) C ) F ( x) f ( x);
2.d f ( x)dx ( f ( x)dx) dx f ( x)dx.
9. Свойства интеграла
3. Неопределенный интеграл отдифференциала непрерывно (x )
дифференцируемой функции равен самой
этой функции с точностью до постоянной:
d ( x) ( x)dx ( x) C,
так как (x ) является первообразной для (x).
10. Свойства интеграла
4.Если функции f1 x и f 2 x имеютпервообразные, то функция f1 x f 2 x
также имеет первообразную, причем
f1 x f 2 x dx f1 x dx f 2 x dx ;
5. Kf x dx K f x dx ;
6. f x dx f x C ;
7. f x x dx F x C .
11. Таблица неопределенных интегралов
1. dx x C .a 1
x
2. x a dx
C, (a 1) .
a 1
dx
3. ln x C .
x
x
a
4. a x dx
C .
ln a
5. e x dx e x C .
6. sin xdx cos x C .
7. cos xdx sin x C .
dx
8. 2 ctgx C .
sin x
dx
9. 2 tgx C .
cos x
dx
arctgx C .
10.
2
1 x
12. Таблица неопределенных интегралов
11.dx
arcsin x C .
1 x 2
dx
1
x
12. 2 2 arctg C .
a
a
a x
13.
14.
15.
dx
a2 x2
x
arcsin C ..
a
dx
1
x a
ln
C
2
2
2a x a
x a
dx
1
a x
a 2 x 2 2a ln a x C .
dx
16.
x2 a
ln x x 2 a C .
17. shxdx chx C .
18. chxdx shx C .
19.
20.
dx
ch 2 x thx C .
dx
cthx C .
2
sh x
13. Свойства дифференциалов
При интегрировании удобно пользоватьсясвойствами: 1
1. dx d (ax)
a
1
2. dx d (ax b),
a
1 2
3. xdx dx ,
2
1 3
2
4. x dx dx .
3
14. Примеры
Пример . Вычислить cos 5xdx .Решение. В таблице интегралов найдем
cos xdx sin x C .
Преобразуем данный интеграл к табличному,
воспользовавшись тем, что d ax adx .
Тогда:
d 5 x 1
= cos 5 xd 5 x =
cos 5xdx cos 5 x
5
5
1
= sin 5 x C .
5
15. Примеры
Пример. Вычислить x3x x 1 dx .
Решение. Так как под знаком интеграла
находится сумма четырех слагаемых, то
раскладываем интеграл на сумму четырех
интегралов:
2
3
2
3
2
3
x
3
x
x
1
dx
x
dx
3
x
dx xdx dx .
x3
x4 x2
3
x C
3
4
2
16. Независимость от вида переменной
При вычислении интегралов удобнопользоваться следующими свойствами
интегралов:
Если f x dx F x C , то
f x b dx F x b C .
Если f x dx F x C , то
1
f ax b dx F ax b C .
a
17. Пример
Вычислим1
6
(
2
3
x
)
dx
(
2
3
x
)
C
.
3 6
5
18. Методы интегрирования Интегрирование по частям
Этот метод основан на формуле udv uv vdu .Методом интегрирования по частям берут такие интегралы:
а) x n sin xdx , где n 1,2...k ;
б) x n e x dx , где n 1,2...k ;
в) x n arctgxdx , где n 0, 1, 2,... k . ;
г) x n ln xdx , где n 0, 1, 2,... k .
При вычислении интегралов а) и б) вводят
n 1
обозначения: x n u , тогда du nx dx , а, например
sin xdx dv ,тогда v cos x .
При вычислении интегралов в), г) обозначают за u функцию
arctgx , ln x , а за dv берут x n dx .
19. Примеры
Пример. Вычислить x cos xdx .Решение.
u x, du dx
=
x cos xdx
dv cos xdx, v sin x
x sin x sin xdx x sin x cos x C .
20. Примеры
Пример. Вычислитьx ln xdx
dx
u ln x, du
x
x2
dv xdx, v
2
x2
x 2 dx
ln x
=
2
2 x
x2
1
x2
1 x2
ln x xdx
ln x
C .
=
2
2
2
2 2
21. Метод замены переменной
Пусть требуется найти f x dx , причемнепосредственно подобрать первообразную
для f x мы не можем, но нам известно, что
она существует. Часто удается найти
первообразную, введя новую переменную,
по формуле
f x dx f t t dt , где x t , а t - новая
переменная
22. Интегрирование функций, содержащих квадратный трехчлен
Рассмотрим интегралax b
dx ,
x px q
содержащий квадратный трехчлен в
знаменателе подынтегрального
выражения. Такой интеграл берут также
методом замены переменных,
предварительно выделив в
знаменателе полный квадрат.
2
23. Пример
Вычислитьdx
.
x 4x 5
Решение. Преобразуем x 2 4 x 5 ,
2
выделяя полный квадрат по формуле a b 2 a 2 2ab b 2 .
Тогда получаем :
x2 4x 5 x2 2 x 2 4 4 5
x 2 2 2 x 4 1 x 2 2 1
x 2 t
dx
dx
dt
x t 2
2
2
2
x 2 1 dx dt
x 4x 5
t 1
arctgt C arctg x 2 C.
24. Пример
Найти1 x
1 x
2
dx
tdt
1 t
2
x t, x t 2 ,
dx 2tdt
2
t2
1 t
2
dt
1 t
1 t
d (t 2 1)
t
2
1
2
2tdt
2
dt
ln(t 1) 2 dt 2
2
1 t
ln(t 2 1) 2t 2arctgt C
2
ln( x 1) 2 x 2arctg x C.
1 t 2 1
1 t
2
dt
25. Определенный интеграл, его основные свойства. Формула Ньютона- Лейбница. Приложения определенного интеграла.
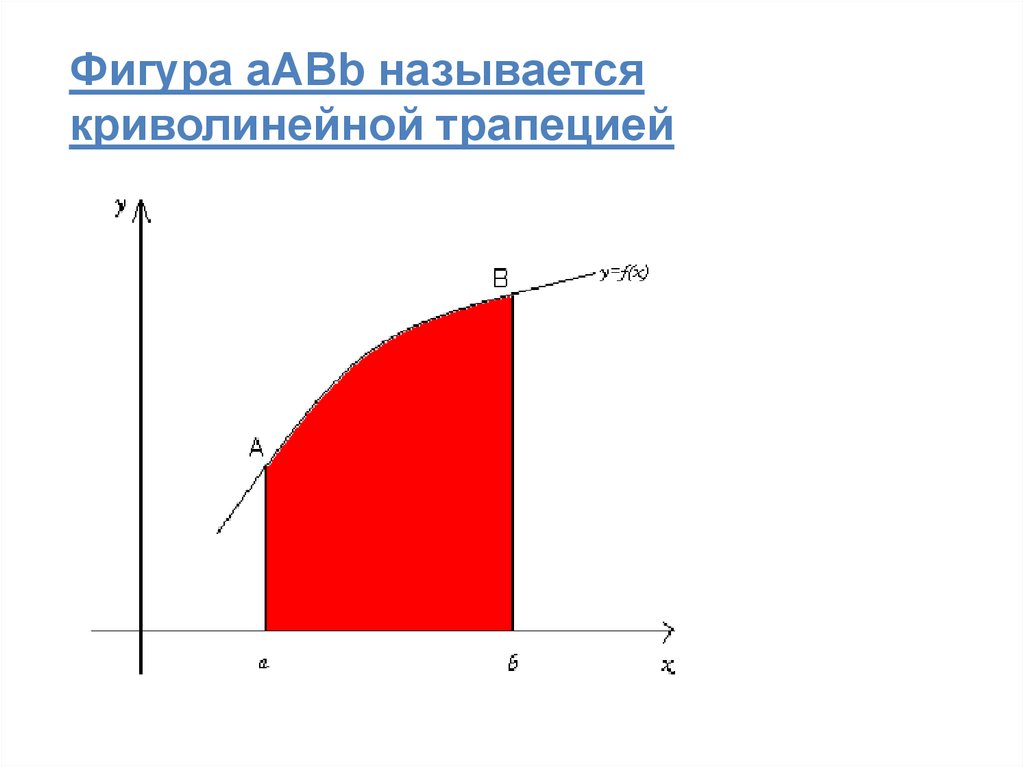
• К понятию определенного интеграла приводитзадача нахождения площади криволинейной
трапеции.
• Пусть на некотором интервале [a,b] задана
непрерывная функция y f ( x ) 0
Задача:
Построить ее график и найти F площадь фигуры,
ограниченной этой кривой, двумя прямыми x = a и x
= b, а снизу – отрезком оси абсцисс между точками
x = a и x = b.
26.
Фигура aABb называетсякриволинейной трапецией
27. Определение
bf ( x)dx
Под определенным интегралом
a
от данной непрерывной функции f(x) на
данном отрезке [a;b] понимается
соответствующее приращение ее
первообразной, то есть
F (b) F (a ) F ( x) /
b
a
Числа a и b – пределы интегрирования, [a;b]
– промежуток интегрирования.
28. Правило:
• Определенный интеграл равен разностизначений первообразной подынтегральной
функции для верхнего и нижнего пределов
интегрирования.
• Введя обозначения для разности
b
F (b) F (a) F ( x) / a
b
f ( x)dx F (b) F (a)
a
Формула Ньютона – Лейбница.
29. Основные свойства определенного интеграла.
1)Величина определенного интеграла не зависит отобозначения переменной интегрирования, т.е.
b
b
a
a
f ( x)dx f (t )dt
где x и t – любые буквы.
2)Определенный интеграл с одинаковыми
пределами
интегрирования равен нулю
a
f ( x)dx F (a) F (a) 0
a
30.
3) При перестановке пределов интегрированияопределенный интеграл меняет свой знак на обратный
b
a
f ( x)dx F (b) F (a) F (a) F (b) f ( x)dx
a
b
(свойство аддитивности)
4) Если промежуток [a;b] разбит на конечное число
частичных промежутков, то определенный интеграл,
взятый по промежутку [a;b], равен сумме определенных
интегралов, взятых по всем его частичным промежуткам.
b
c
b
f ( x)dx f ( x)dx
c
a
a
f ( x)dx
31.
5)Постоянный множитель можно выноситьза знак определенного интеграла.
6)Определенный интеграл от алгебраической
суммы конечного числа непрерывных
функций равен такой же алгебраической
сумме определенных интегралов от этих
функций.
32. 3. Замена переменной в определенном интеграле.
3. Замена переменной в определенноминтеграле.
b
f ( x)dx f (t ) (t )dt
a
a ( ), b ( ), (t ) [a; b]
где
для t [ ; ] , функции (t ) и (t ) непрерывны на ;
5
Пример:
1
=
x 1dx
=
x 1 5
t 0 4
x 1 t
dt dx
4
0
3
2
t dt t 2
3
4
0
2
2
16
1
t t 40 4 2 0
5
3
3
3
3
33. Несобственные интегралы.
Несобственные интегралы.Определение. Пусть функция f(x) определена на
бесконечном интервале [a; + ) и интегрируется
на любом интервале [a;b], где b < + . Если
существует
b
lim
f ( x)dx,
b
a
то этот предел называется несобственным
интегралом функции f(x) на интервале
[a; + ) и обозначается
f ( x.)dx
a
34.
• Таким образом, по определению,b
f ( x)dx lim f ( x)dx lim ( F (b) F (a))
a
b
a
b
Если этот
предел некоторое
число, то
интеграл
f ( x)dx
a
называется
сходящимся, если предела не существует, или он равен ,
то говорят, что интеграл расходится.
35. Пример. Интеграл Пуассона:
ex2
a2
dx
• если а = 1, то
e
x2
dx
• Интеграл сходится, и его значение
.
36. 5. Приложения определенного интеграла
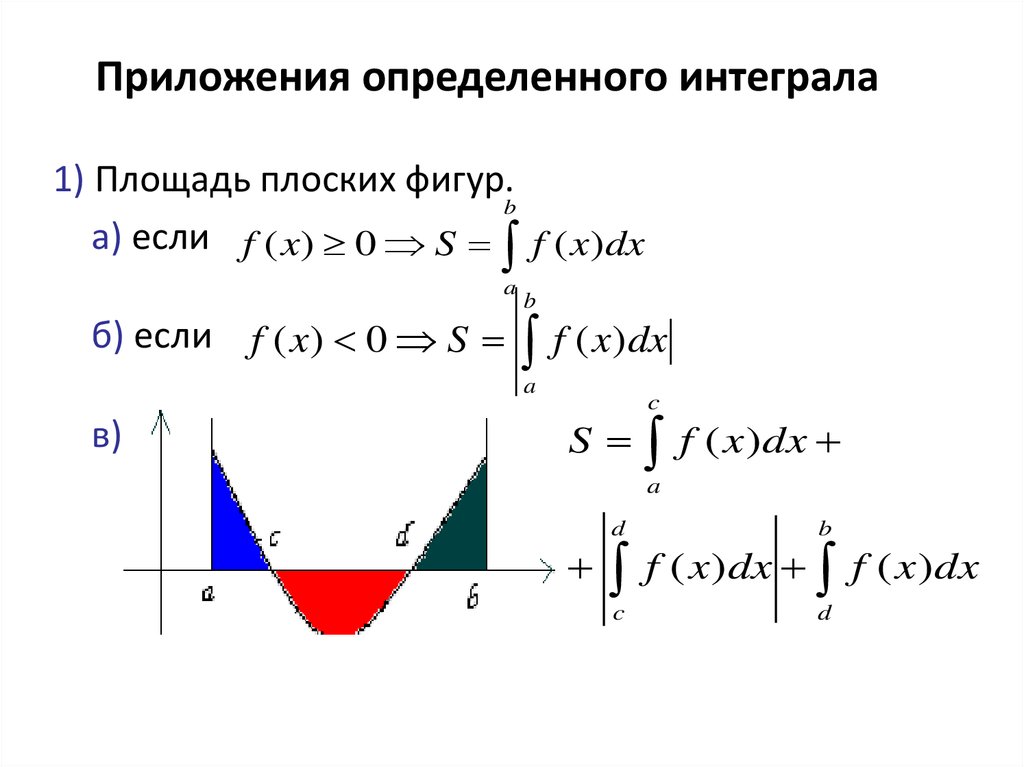
1) Площадь плоских фигур.b
а) если f ( x) 0 S f ( x)dx
a
б) если f ( x) 0 S
b
f ( x)dx
a
в)
c
S
f ( x)dx
a
d
b
c
d
f ( x)dx f ( x)dx
37.
bг) S f ( x) ( x) dx
a
2) Многие физические величины можно
определить и задать через понятие
интеграла. Например, работа для любой
силы вычисляется как интеграл от величины
b
силы по длине пути.
A F ( x)dx
a
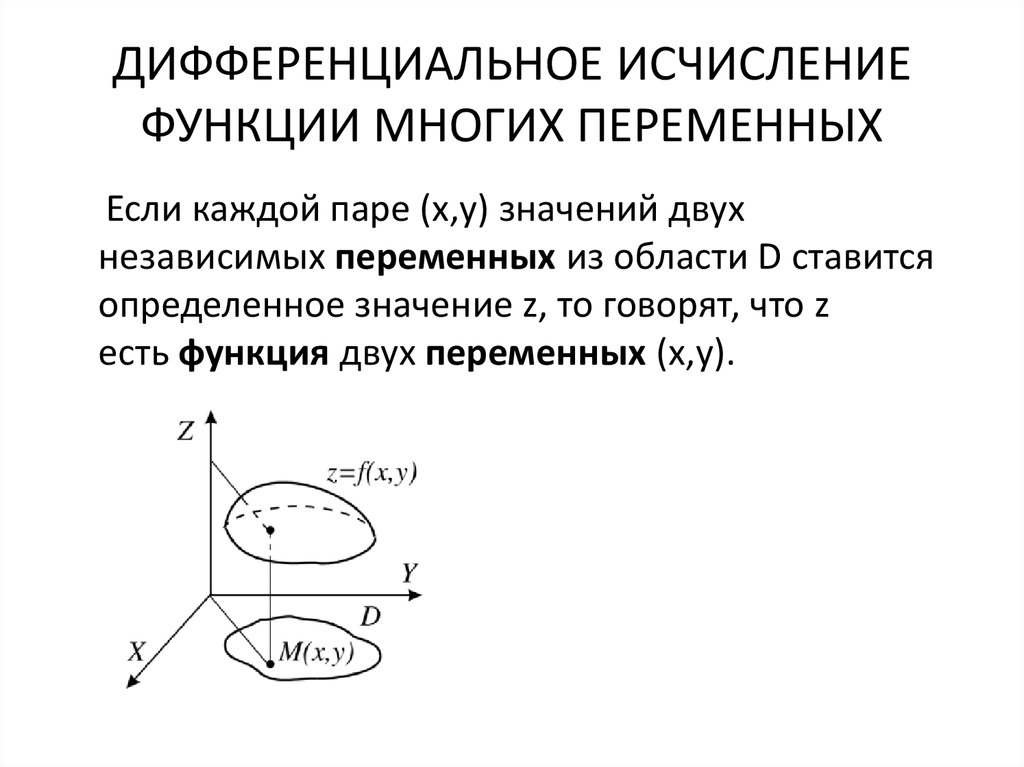
38. ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ ФУНКЦИИ МНОГИХ ПЕРЕМЕННЫХ
Если каждой паре (x,y) значений двухнезависимых переменных из области D ставится
определенное значение z, то говорят, что z
есть функция двух переменных (x,y).
39. Частные приращения и частные производные
x z f ( x x, y ) f ( x, y )xz
lim
x 0 x
z
f ( x, y )
; z x ;
;
x
x
f x ( x, y ).
y z f ( x, y y) f ( x, y)
lim
y 0
yz
y
z
f ( x, y)
; z y ;
;
y
y
f y ( x, y).
40. Полное приращение функции 2-х переменных
Если обеим переменным датьприращение, то функция получит
полное приращение
z f ( x x, y y ) f ( x, y )
41. Полное приращение и полный дифференциал
z f ( x x, y y) f ( x, y)dz f x ( x, y)dx f y ( x, y)dy
z
z
dz dx dy
x
y
u
u
u
du
dx dy dz
x
y
z
42. Дифференциалы высшего порядка
Дифференциалом второго порядкафункции z=f(x,y) называется
d 2 z d (dz )
n 1
Вообще: d z d (d z )
Если х и у независимые переменные, то
2
2
2
.
d z z dx 2z dxdy z dy
n
xx
xy
yy
43. Экстремумы функции двух переменных
Определение. Говорят, что в точке P0 ( x0 , y0 )функция f (x,y) имеет максимум, если cуществует
такая окрестность этой точки, что для всех точек
P(x,y) этой окрестности, отличных от P0 ( x0 , y0 ) ,
выполнено неравенство
f ( P0 ) f ( P).
Аналогично определяется минимум функции.
Минимум и максимум функции называются ее
экстремумами.
44. Экстремумы функции двух переменных
Теорема (необходимое условиеэкстремума). В точке экстремума функции
нескольких переменных каждая ее частная
производная либо равна нулю, либо не
существует.
Точки, в которых выполнены эти условия,
называются критическими.
45. Достаточные условия экстремума функции двух переменных
Теорема. Пусть функция z=f(x,y) определена и имеет непрерывныечастные производные до 3-го порядка в некоторой окрестности точки
M 0 ( x0 , y 0 )
, в которой z x z y 0 . Если при этом в этой точке
выполнено условие
z xx z yy ( z xy ) 2 0
, то точка M 0
является точкой экстремума функции, причем точкой максимума, если
z xx 0
, и точкой минимума, если
Если же в этой точке
z xx 0
.
z xx z yy ( z xy ) 2 0 , то
экстремума в точке
M 0 нет.
В том случае, если z xx z yy ( z xy ) 0 в точке M 0 , теорема ответа
2
не дает.
46. Пример
Исследовать на экстремум функцию50 20
z xy , åñëè x 0 u y 0.
x
y
47. Наибольшее и наименьшее значения функции
Определение. Наименьшее или наибольшеезначение функции в данной области
называется абсолютным экстремумом
функции (абсолютным минимумом или
абсолютным максимумом соответственно)
в этой области.
48.
Известно, что непрерывная взамкнутой ограниченной области
функция достигает в ней своих
наибольшего и наименьшего
значений.
Абсолютный экстремум достигается
функцией либо в критических точках,
либо на границе области.
49.
Пусть функция непрерывна в замкнутойограниченной области G, дифференцируема внутри
этой области. Чтобы найти наибольшее и
наименьшее значения функции в этой области,
нужно:
1)найти критические точки, принадлежащие этой
области, и вычислить в них значения функции;
2)найти наибольшее и наименьшее значения функции
на границе области;
3)из всех найденных значений выбрать наибольшее и
наименьшее.
50. Скалярное поле Основные определения
Пусть в области D пространства Охуzзадана функция u=u(х,у,z). В этом случае
говорят, что в области D задано скалярное
поле, а саму функцию u=u(х,у,z)называют
функцией поля. Например, поле давлений,
температур и т.д.
51. Скалярное поле Основные определения
Множество точек М области D, для которыхскалярное поле сохраняет постоянное
значение, т. е. u(М)=С, называется
поверхностью уровня ( или
изоповерхностью) скалярного поля.
52.
Если область D расположена на плоскостиОху, то поле u=u(х,у) является плоским.
Поверхности уровня называют в этом
случае линиями уровня.
53.
Пусть2
f( x y) x y
2
f
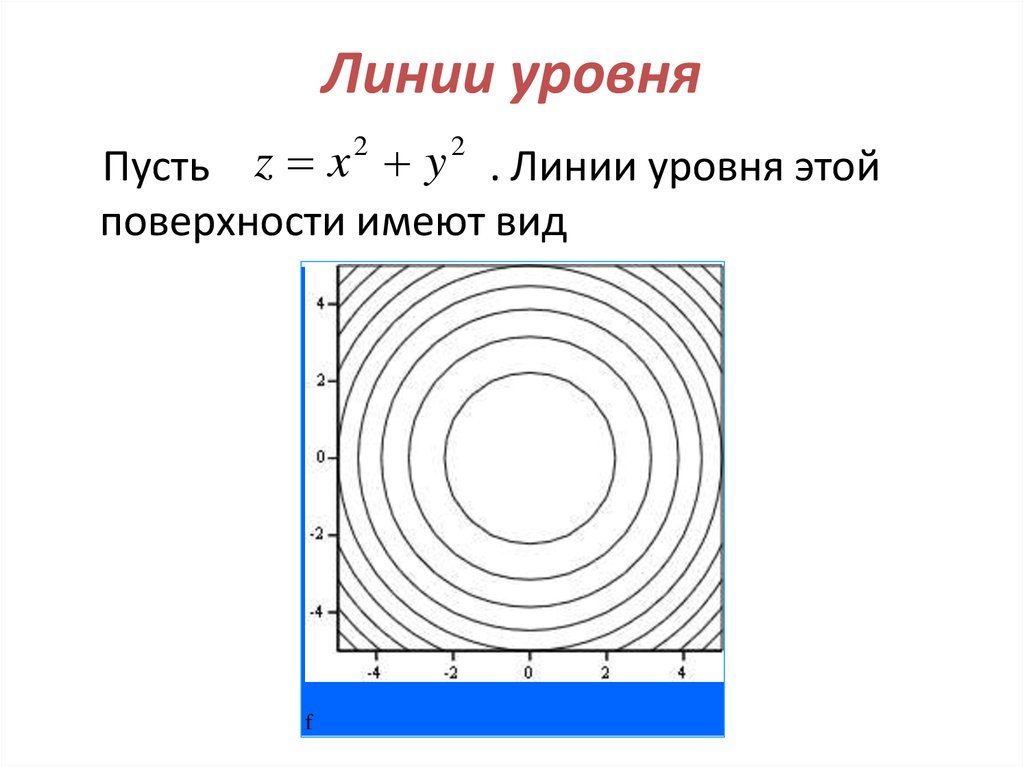
54. Линии уровня
Пусть z x y . Линии уровня этойповерхности имеют вид
2
f
2
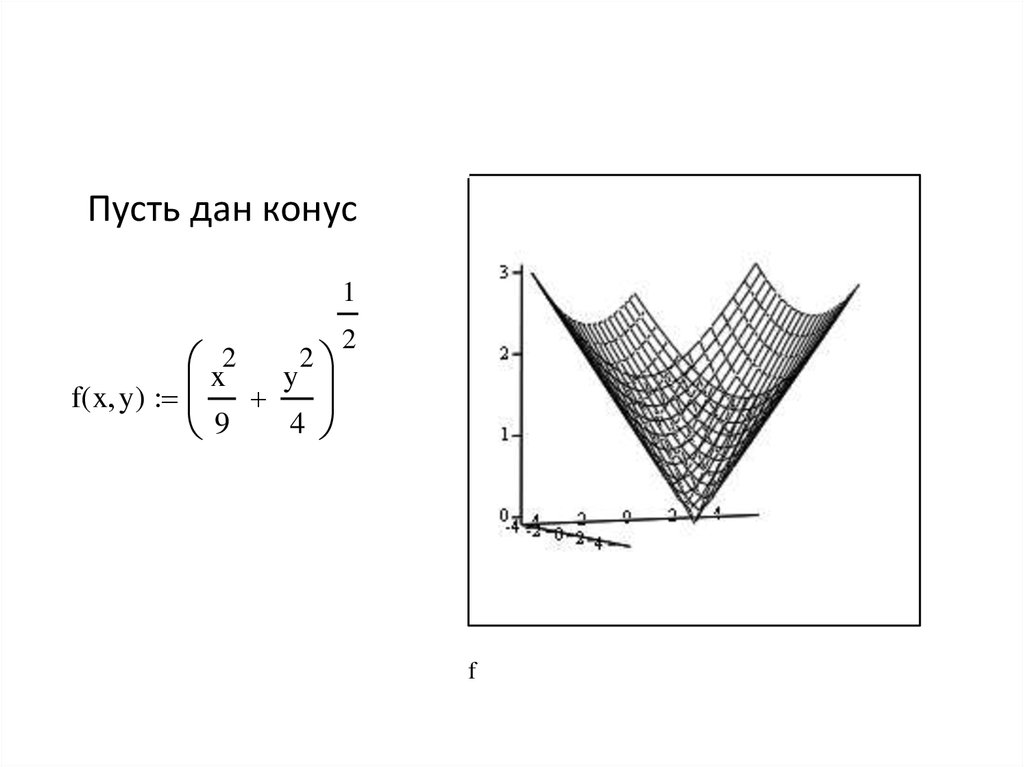
55.
Пусть дан конус1
x
y
f( x y )
4
9
2
2
2
f
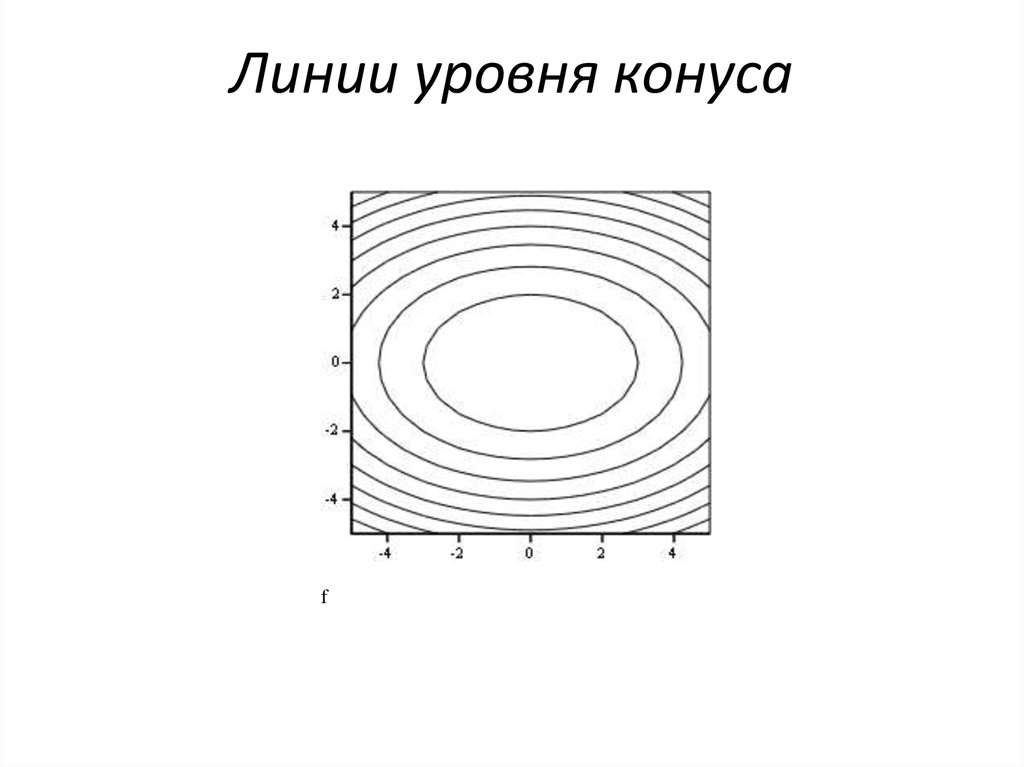
56. Линии уровня конуса
f57.
Пусть задана дифференцируемая функцияскалярного поля. u u x, y, z
Рассмотрим точку P x, y, z этого поля и луч
, выходящий из точки P в направлении
единичного вектора
0 cos α; cos β; cos γ ,
где
0
α, β, γ –углы, образованные вектором
с осями координат .
58. Определение
zP1
γ
ℓ
β
P
α
0
x
x
y
Рис.
Пусть P1 x x , y y , z – z
какая-нибудь другая точка
этого луча. Обозначим
PP1 x 2 y 2 z 2
– расстояние между точками
P и Ρ1 ; называют
величиной перемещения.
Приращением функции в
направлении назовем
разность
u u Ρ1 u Ρ
59.
Производной функции u u x, y, zв точке P по направлению называется
предел отношения приращения функции в
направлении
к величине перемещения при 0 :
u
u
lim
0 .
60. Вычисление производной по направлению
Формула вычисления производной понаправлению:
u u
u
u
cos cos cos , ãäå
x
y
z
ly
lx
lz
cos , cos , cos ,
l
l
l
l lx2 l y2 lz2 .
61. Градиент скалярного поля
Градиентом скалярного поля u=u(x,y,z), гдеu=u(x,y,z)-дифференцируемая функция,
называется вектор с координатами
u u u .
, ,
x y z
Таким образом,
u u u
gradu ( , , )
x y z
или
.
u
u
u
gradu
x
i
y
j
z
k
62. Пример
22
Найти градиент функции u= x y z
M(6,2,3).
Решение. Вычислим градиент функции.
u
x
x
u
z
Тогда grad u =
А в точке М
в точке
y
u
y
x2 y 2 z 2
2
x2 y 2 z 2
z
x2 y 2 z 2
x
x2 y2 z 2
i+
y
x2 y2 z 2
j +
6 2
3
gradu i j k .
7 7
7
z
x2 y2 z 2
k
63. Направление градиента
Теорема. Производная функции понаправлению ul равна проекции
градиента этой функции на данное
направление (в соответствующей
точке).
64. Направление градиента
Так как производная по направлениюпредставляет собой скорость изменения функции
в данном направлении , а проекция вектора на
другой вектор имеет максимальное значение,
если оба вектора совпадают по направлению, то
градиент функции в данной точке указывает
направление наиболее быстрого возрастания
функции.
65. Величина градиента плоского скалярного поля
Величина градиента плоского скалярногополя ,т.е.
2
2
u u
grad u =
x y
обозначается tg и определяет крутизну
наибольшего ската или подъема
поверхности u = f (x, y).
66.
Градиент скалярного поля в данной точке повеличине и направлению равен
максимальной скорости изменения поля в
этой точке, т. е.
u u
,
max
gradu
l
где
l
l *
.
l gradu
*
67. Обыкновенные дифференциальные уравнения
Обыкновеннымдифференциальным
уравнением
называется уравнение, связывающее между собой
значения независимой переменной x, неизвестной
функции y = f(x) и её производных (или
дифференциалов):
Порядком уравнения называется максимальный порядок n
входящей в него производной (или дифференциала).
Функция y(x) называется решением (или интегралом)
дифференциального уравнения если при подстановке ее в
уравнение обращает его в тождество.
Пример: y(4) – y + x = 0 - уравнение четвёртого порядка.
68.
ОДУ первого порядкаОбыкновенным дифференциальным уравнением
первого порядка называется уравнение вида:
где x - независимая переменная, y(x) - неизвестная функция
Общее решение:
Пример:
y ( x) 3 x 0
общее решение:
y ( x)
3 2
x c
2
69.
Разделяют несколько типов (видов) обыкновенныхдифференциальных уравнений:
-Уравнения с разделяющимися переменными,
-Однородные уравнения,
-Линейные уравнения,
-Уравнение в полных дифференциалах,
-и т.д.
Остановимся подробнее на каждом из этих типов
уравнений.
70.
Уравнения с разделёнными переменными.Так называются уравнения вида удовлетворяющее
начальному условию
f(x)dx + g(y)dy = 0,
Интегрируя, получим
- общий интеграл (общее решение) этого
уравнения.
Пример:
e y dy ( x3 7 x) dx 0;
x4 7 2
e
x c 0
4 2
y
e y dy ( x 3 7 x) dx 0;
- общее решение
71.
Уравнения с разделяющимися переменными.Так называются уравнения вида
Эти уравнения легко сводятся к уравнению с разделёнными
переменными:
Записываем уравнение в форме:
затем делим на g(y) и умножаем на dx:
.
Это уравнение - с разделёнными переменными. Интегрируя,
получим общий интеграл:
72.
Пример:Выразим у из последнего выражения как функцию х, получим
общее решение:
73.
Уравнения с однородной правой частью. Так называются уравнения соспециальным видом зависимости функции f(x, y) от своих аргументов:
Это уравнение сводится к уравнению с разделяющимися переменными
относительно новой неизвестной функции u(x) заменой:
Подставляя в уравнение y = x·u, y ′ = u + x·u ′, получим
(это - уравнение с разделяющимися переменными),
- это общий интеграл уравнения относительно переменных x, u
74.
Пример:- общее решение уравнения
75.
Пример:Окончательно, получим общее решение:
76.
Линейные уравнения. ДУ первого порядка называется линейным,если неизвестная функция y(x) и её производная входят в уравнение
в первой степени:
здесь p(x), q(x) - непрерывные функции.
Пример:
dy
sin( x) y ctg ( x);
dx
y (1 x 2 ) y 37 x 5.
77.
Для решения уравнения представим y(x) в виде произведения двух новыхнеизвестных функций u(x) и v(x): y(x) = u(x)v(x).
Тогда
и уравнение приводится к виду:
или
Это уравнение решаем в два этапа: сначала находим функцию v(x) как
частное решение уравнения с разделяющимися переменными:
затем находим u(x) из уравнения:
78.
Отметим, решая уравнение на v(x) мы не вводим в это решениепроизвольную постоянную C, нам достаточно найти одну функцию v(x),
обнуляющую слагаемое со скобками.
Запоминать эту формулу не
надо, лучше усвоить порядок действий и воспроизводить его при решении
каждой задачи.
79.
Пример:Решение:
и общее решение уравнения
.
80.
Для нахождения частного решения, соответствующегоначальным условиям (задача Коши), подставим в общее
решение
Решение задачи:
81.
Уравнение в полных дифференциалах. Так называется уравнение видаP(x, y) dx + Q(x, y) dy = 0.
(P(x, y), Q(x, y) - непрерывно дифференцируемы) в случае, если его левая
часть является полным дифференциалом некоторой функции u(x, y), т.е.
если существует такая функция u(x, y), что
Необходимым и достаточным условием существования такой функции
является условие:
Если - уравнение в полных дифференциалах, то его правая часть равна 0,
т.е. принимает вид du(x, y) = 0. На решении y(x) получим du(x, y(x)) = 0,
следовательно, u(x,y(x)) = C, где C - произвольная постоянная.
Соотношение u(x, y) = C и есть общее решение уравнения в полных
дифференциалах.
82.
Для нахождения функции u(x, y) решается система уравненийИз первого уравнения этой системы находим:
с точностью до произвольной дифференцируемой по y
функции
(эта функция играет роль постоянной интегрирования;
так как интегрирование ведётся по переменной x.
Дифференцируем эту функцию по y и приравниваем выражению,
стоящему во втором уравнении системы (т.е.
), получим
дифференциальное уравнение из которого можно найти
.
83.
Пример: найти общее решение уравненияУбедимся, что это - уравнение в полных дифференциалах.
.
84.
ОДУ высших порядковОбыкновенным дифференциальным уравнением называется
уравнение, связывающее между собой значения независимой
переменной x, неизвестной функции y = f(x) и её производных
(или дифференциалов):
Общим решением (общим интегралом) уравнения называется
соотношение вида:
85.
Некоторые типы уравнений, допускающие понижение порядка.Уравнение вида
решается последовательным n-кратным интегрированием.
Пример:
Переобозначив постояные, общее решение запишем в виде :
y = cos x + C1x3 + C2x2 + C3x + C4.
86.
Уравнение, не содержащее в явном виде неизвестную функцию и еёмладшие производные.
Порядок уравнения вида F(x, y(k), y(k+1), y(k+2), …,y(n)) = 0, не содержащего
функции y(x) и (k – 1) младшую производную этой функции в явном виде,
может быть понижен ровно на k единиц введением новой неизвестной
функции
z(x) = y(k)(x). Тогда уравнение примет вид
т.е. будет уравнением (n – k)-го порядка.
После нахождения z(x) последовательным интегрированием решается
уравнение y(k)(x)= z(x).
87.
Пример: Понизить порядок уравнения:Младшая производная, входящая в явной форме в уравнения, - вторая,
поэтому делаем замену искомой функции:
Тогда:
и уравнение примет вид
88.
Уравнение, не содержащее в явном виде независимую переменную x.Порядок уравнения
не содержащего явно x, может быть понижен на 1 с помощью приёма,
который заключается в том, что вводится новая функциональная
зависимость от y:
Пример: Понизить порядок уравнения:
Переменная x явно в уравнение не входит, поэтому полагаем
тогда
.
Просто сократить на p это уравнение нельзя, так как можно потерять
семейство решений
поэтому рассматриваем два случая:
,


















































































 mathematics
mathematics








