Similar presentations:
Неопределенный интеграл и его свойства
1. Неопределенный интеграл и его свойства
2.
Иога́нн Берну́лли(27.07.1667-1.01.1748)
— швейцарский
математик и
механик,
в 1696 году
предложил
термин
«интеграл»
3.
Леона́рд Э́йлер(15.04.1707 — 7.09.1783)
— швейцарский,
немецкий и российский
математик и механик,
ввёл обозначение
неопределённого
интеграла
4. Интегрирование – операция отыскания функции по её производной.
5.
Определение. Функция F x называетсяпервообразной функции f x ,
определенной на некотором промежутке,
если F x f x для каждого x из этого
промежутка.
6.
Очевидно, если F x - первообразнаяфункции f x , то F x C , где C некоторая постоянная, также является
первообразной функции f x .
Если F x есть какая-либо первообразная
функции f x , то всякая функция вида
Ф x F x C также является
первообразной функции f x и всякая
первообразная представима в таком виде.
7.
Определение. Совокупность всехпервообразных функции f x ,
определенных на некотором
промежутке, называется
неопределенным интегралом от
функции f x на этом промежутке и
обозначается f x dx .
8.
f x dx F x C - неопределённый интегралгде
- знак интеграла,
f(x) - подынтегральная функция,
f(x)dx - подынтегральное выражение,
F(x) - первообразная функции,
С - постоянная интегрирования
9. Свойства неопределённого интеграла:
( f ( x) g ( x))dx f ( x)dx g ( x)dx2. kf ( x)dx k f ( x)dx
3. Если f ( x)dx F ( x) C , то
1
f (ax b)dx a F (ax b) C
1.
10. Таблица неопределенных интегралов:
1. dx x C .a 1
x
2. x a dx
C, (a 1) .
a 1
dx
3. ln x C .
x
x
a
4. a x dx
C .
ln a
5. e x dx e x C .
6. sin xdx cos x C .
7. cos xdx sin x C .
dx
8. 2 ctgx C .
sin x
dx
9. 2 tgx C .
cos x
dx
arctgx C .
10.
2
1 x
11. Таблица неопределенных интегралов:
11.dx
1 x
arcsin x C .
2
dx
1
x
12. 2 2 arctg C .
a
a
a x
13.
dx
x
arcsin C .
a
a2 x2
dx
1 x a
C
14. 2 2 ln
2a x a
x a
dx
1 a x
C .
15. 2 2 ln
2a a x
a x
16.
dx
x2 a
ln x x 2 a C .
12. Методы интегрирования:
1.Непосредственное интегрирование(на основании формул интегрирования и
свойств неопределённого интегрирования).
2.Замена переменных
(интегрирование . через вспомогательную
переменную).
3. Интегрирование по частям:
udv uv vdu
13.
Пример. Вычислить x 3x x 1 dx .Решение. Так как под знаком интеграла
находится сумма четырех слагаемых, то
раскладываем интеграл на сумму четырех
интегралов:
2
3
2
3
2
3
x 3x x 1 dx x dx 3 x dx xdx dx .
3
4
2
x
x x
3 x C
3
4 2
14. Пример. Вычислить
2 x 1dxРешение.
3
2x 1 t
3
dt 1 12
1 t2
1 32
1
2
2
x
1
dx
2
dx
dt
t
t
dt
C
t
C
(
2
x
1
)
C
2 2
23
3
3
dt
2
dx
2
15.
Пример. Вычислить x cos xdx .Решение.
u x, du dx
=
x cos xdx
dv cos xdx, v sin x
x sin x sin xdx x sin x cos x C .
16.
Пример. Вычислитьdx
u ln x, du
x2
x 2 dx
x
ln
x
=
x ln xdx
2
2 x
x2
dv xdx, v
2
2
2
2
x
1
x
1x
ln x xdx
ln x
C .
=
2
2
2
2 2














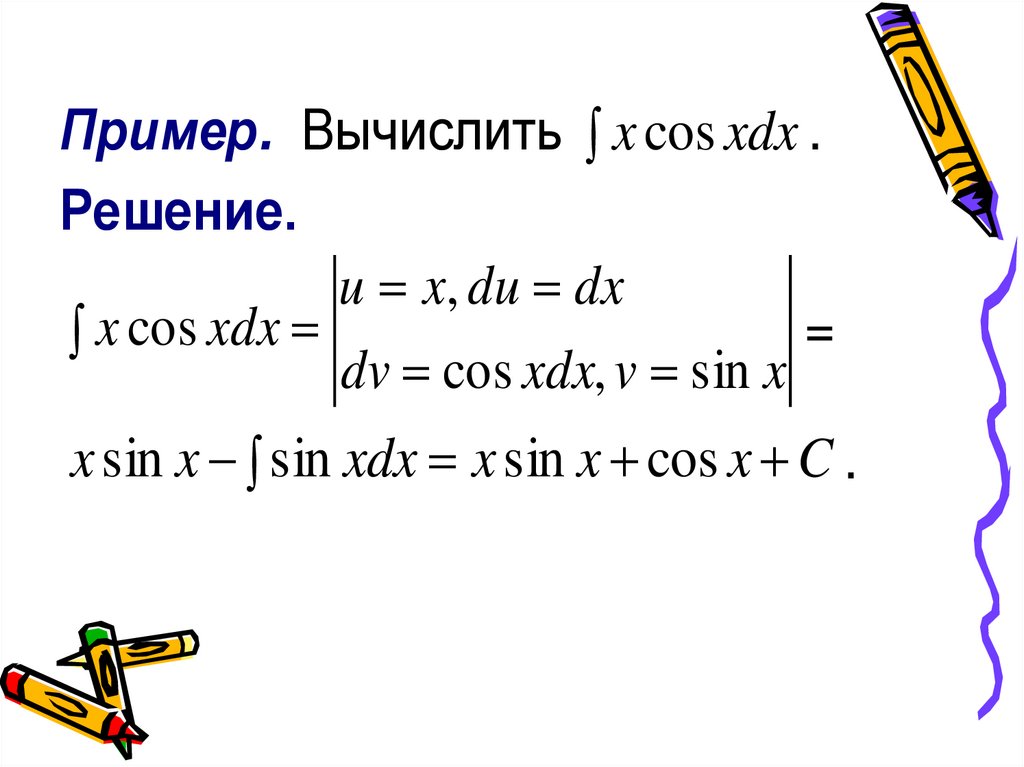



 mathematics
mathematics








