Similar presentations:
Определённый интеграл. Свойства определённого интеграла
1. Определённый интеграл Свойства определённого интеграла
2.
1.b
a
a
b
f ( x)dx f ( x)dx
a
f ( x) 0
2.
a
3.
b
b
a
a
kf ( x)dx k f ( x)dx , k-любое число
3.
4.b
b
b
a
a
a
( f1 ( x) f 2 ( x))dx f1 ( x)dx f 2 ( x)dx
5.Аддитивность определённого интеграла. Для
любых чисел a,b,c справедливо:
b
c
b
a
a
c
f ( x)dx f ( x)dx f ( x)dx
4.
a; b6) Если на
, то
f x 0
f x dx 0.
b
a
7) Если на
f x x
a; b
f x dx x dx
b
b
a
a
5. Теорема о среднем
Если функция непрерывна на [ a, b], тосуществует такая точка C [a, b],
b
что
f ( x)dx f (C )(b a).
a
y f (x)
a
C
b
6. Формула Ньютона-Лейбница.
Если F(x) есть какая-либопервообразная
от непрерывной на [ a, b] функции
f(x), то справедлива формула
Ньютона-Лейбница:
b
f ( x)dx F (b) F (a)
a
7.
Пример.0, 5
dx
1 x arcsin x
2
0
0,5
0
arcsin 0,5 arcsin 0
6
8. Методы интегрирования
9.
x z9
dx 2 z dz 3 2 z dz
dx
4
x 1 x 2; z 2 2 z 1
x 9; z 3
2
z 1 1
1
2
dz 2 1
dz
3
3
z 1
2
2
z 1
9
2 z 2 2ln z 1 2 6 4 2 ln 4 2 ln 3 2 ln
16
3
3
10. Интегрирование по частям в определённом интеграле.
bb
udv
u
v
vdu
a
b
a
a
11.
u x; du dxx cos x dx dv cos x dx
0
v cos x dx sin x
x sin x 0 sin x dx
0
sin 0 sin 0 cos x 0
0 0 cos cos0 1 1 2
12. Геометрические приложения определенного интеграла
13.
a; by f x
• 1. Если
непрерывна и
положительна, то
с основанием
кр .тр .
ограниченной сверху графиком
этой функции можно найти по формуле
S
S f x dx
b
a
14.
2. Еслиf x 0 на a; b .
f x 0
S f x dx f x dx
b
b
a
a
b
S f ( x) dx
a
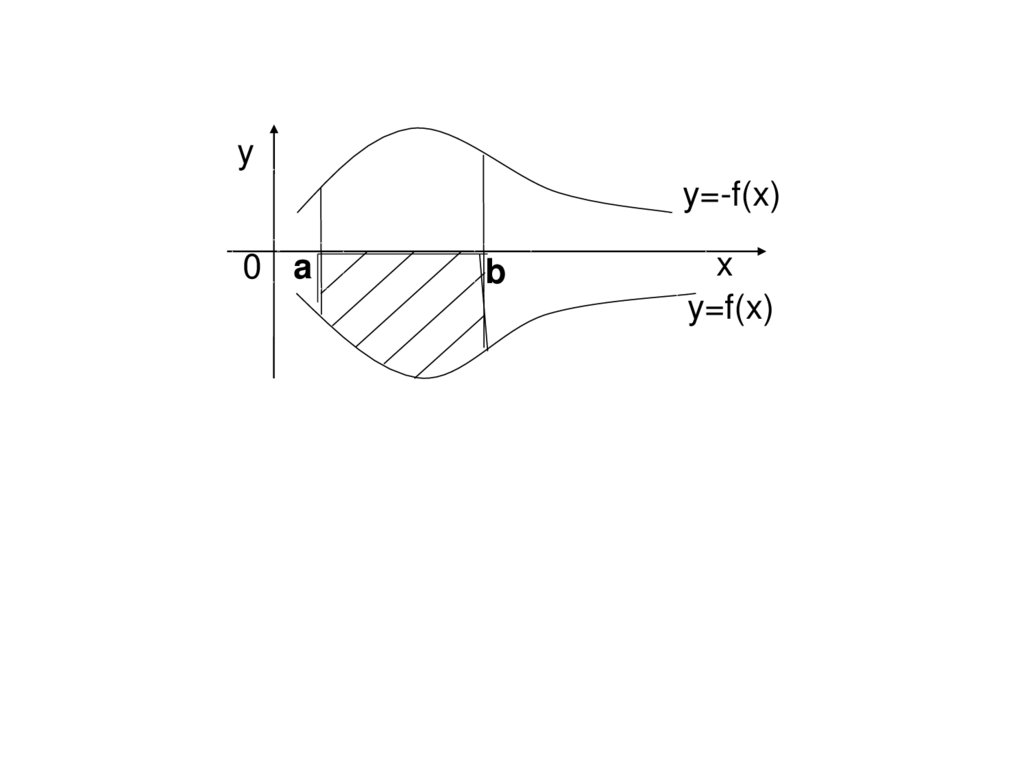
15.
yy=-f(x)
0 a
b
x
y=f(x)
16.
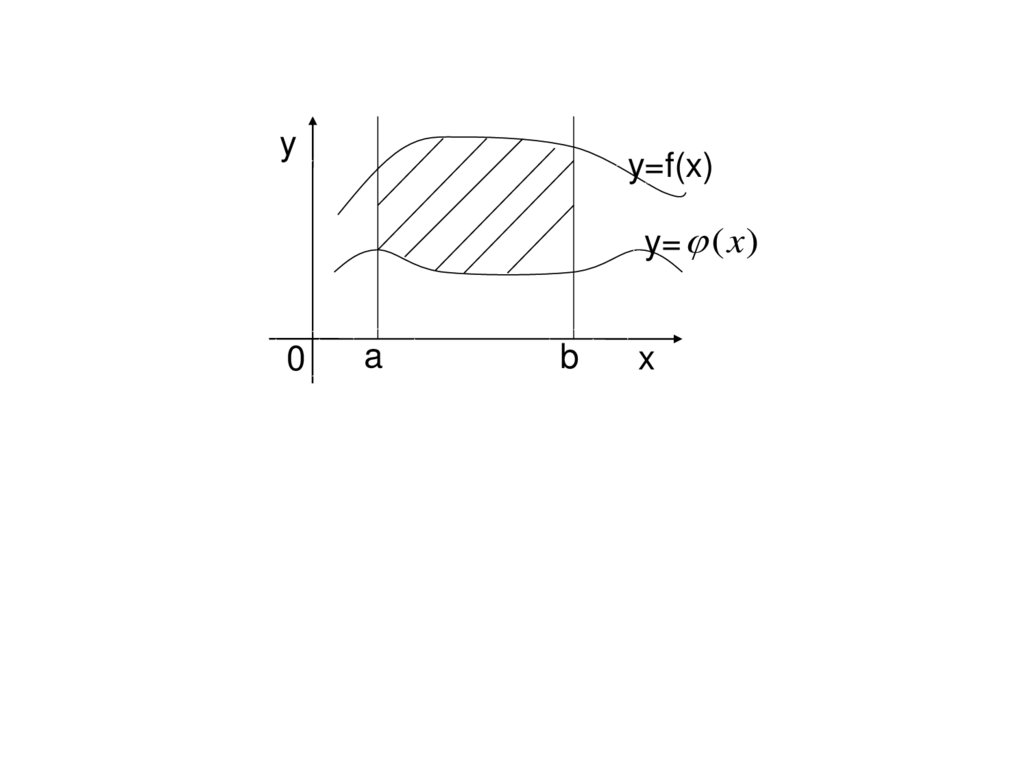
3.Рассмотрим случай, когда фигураограничена сверху графиком функции
, снизу графиком функции
b
y f x
y x .
S f ( x) ( x)dx
a
17.
yy=f(x)
y= (x )
0
a
b
x
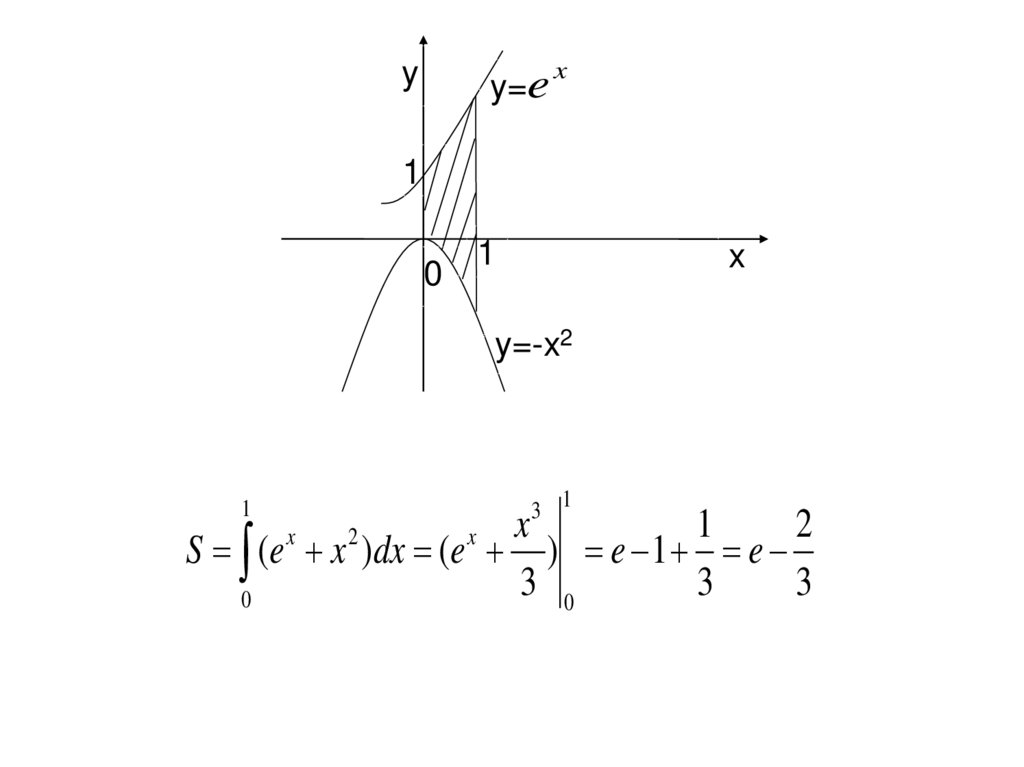
18.
yy=e
x
1
1
0
x
y=-x2
3 1
1
x
1
2
S (e x )dx (e ) e 1 e
3 0
3
3
0
x
2
x
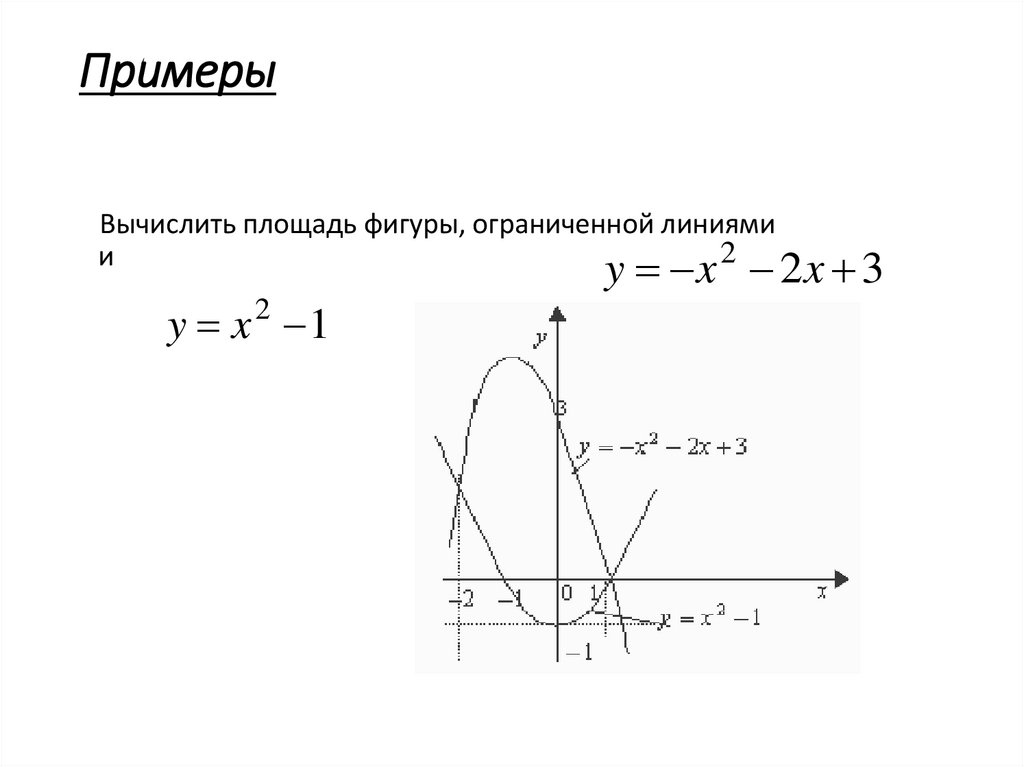
19. Примеры
Вычислить площадь фигуры, ограниченной линиями2
и
y x 2x 3
y x 2 1
20.
Получим1
1
2
S x 2 2 x 3 x 2 1 dx 2 x 2 x 4 dx
2
2
1
x
x
2 x
2 x x 2 dx 2
2
2
3
2
1
2
3
2
1 1
8
8 4
1 1
2 2 4 2 2 6
3
3 2
3 2
3 2
1
9
2 3 8 2 9
2
2
21. Вычисление площадей
В случае параметрического заданиякривой, площадь фигуры, ограниченной
прямыми x a, x b, осью Ох и кривой
x (t ), y (t ),вычисляют по
t2
формуле
S (t ) (t )dt ,
t1
где пределы интегрирования определяют из
уравнений
a (t1 ), b (t 2 ) .
.
22. Пример.
22
x
y
Найти площадь эллипса
.
1
2
2
a
b
Параметрические уравнения эллипса
x a cos t , y b sin t.
S 4 b sin t ( a sin t )dt
/2
у
/2
b
х
о
0
a
/2
1 cos 2t
4ab sin tdt 4ab
dt
2
0
0
2
1
1
/2
4ab(t sin 2t ) 0 2ab ab.
2
2
2
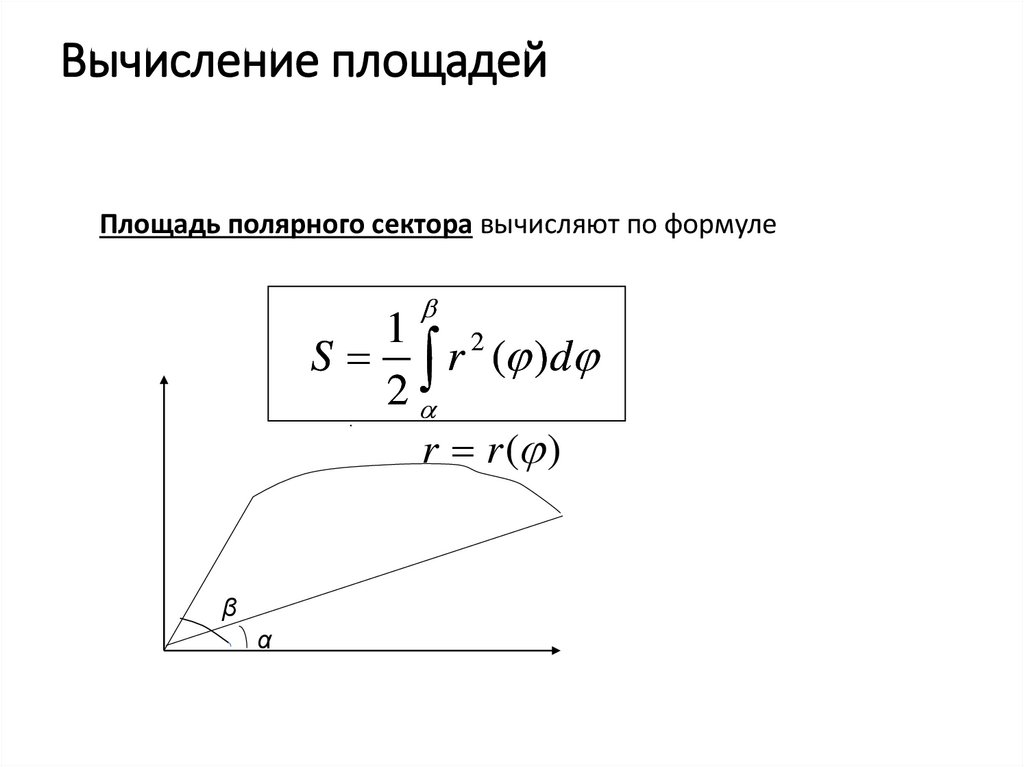
23. Вычисление площадей
Площадь полярного сектора вычисляют по формуле1 2
S r ( )d
2
r r ( )
.
β
α
24. Пример.
Площадь фигуры, ограниченнойи лежащей вне круга радиуса
:
лемнискатой Бернулли
2
2
r a cos 2
r
a
2
/6
/6
/6
2
1
1 a
1 2
1 2
2
a cos 2 d
d ( a sin 2 a )
2 0
2 0 2
4
4
0
1 2
a2
3
a2
a (sin )
(
)
( 3 )
4
3 6
4 2 6
8
3
a2
S
( 3 )
2
3
25. Вычисление длины дуги
Если кривая задана параметрическимиуравнениями x t , y t , то длина
ее дуги
t
2
l
2
2
t t dt
t1
где t1 ,t 2 –значения параметра,
соответствующие концам дуги .
26. Длина дуги в декартовых координатах
Если кривая задана уравнением y f x ,b
то
2
l
1 f x dx
a
где a, b–абсциссы начала и конца дуги a b .
Если кривая задана уравнением x g y ,
d
то
,
2
l
c
1 g y dy
где c, d–ординаты начала и конца дуги c d .
27. Длина дуги в полярных координатах
Если кривая задана уравнением в полярных координатахто
где
дуги .
l
2
2 d
–значения полярного угла, соответствующие концам
,
,
28. Пример.
y xВычислить длину дуги кривой
от точки
до
.
B 4,8
O 0,0
, 3тогда1
y x x 2
2
4
4
4
9 9
9
l 1 x dx
1 xd 1 x
4
90
4 4
0
3
2
4 2 9
1 x
9 3 4
3
2
4
8
10 10 1
27
0
3
29. Вычисление объема тела вращения.
Объем тела, образованного вращением вокруг оси Oxкриволинейной трапеции, ограниченной кривой
,
отрезком оси абсцисс
и прямыми
, вычисляется
по формуле
y f x
a x b
x a, x b
b
Vx π
f x dx
2
a
30.
Yf x
a
x
b
X
31. Вычисление объема тела вращения
Объем тела, образованного вращением вокруг оси Oy фигуры,ограниченной кривой
, отрезком оси ординат
и
прямыми
, вычисляется по формуле
x g y
y c, y d
c y . d
d
Vy
g
y
dy
2
c
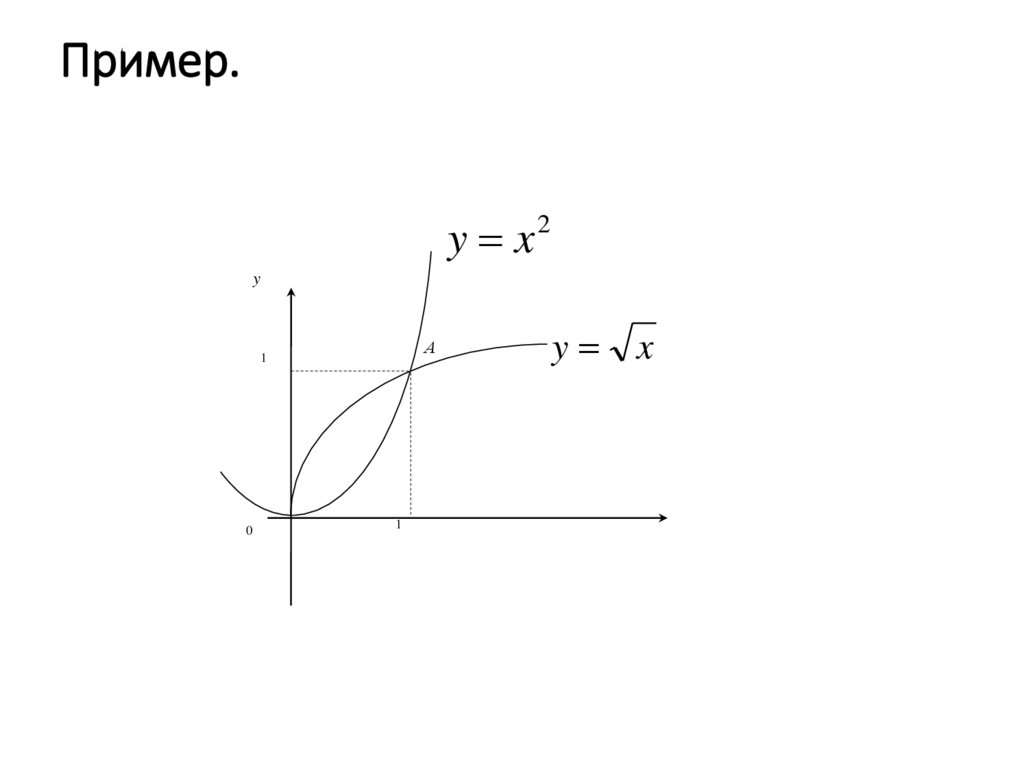
32. Пример.
y x2y
А
1
0
1
y
x
33.
Искомый объем можно найти как разностьобъемов, полученных вращением вокруг
оси Ox криволинейных трапеций,
ограниченных линиями y x и
34. Решение.
x dx x dx1
Тогда
Vx
1
1
1
2
0
0
2 1
x
xdx x dx
2
0
0
4
3
2 5 10
0
2 2
5 1
x
5
0

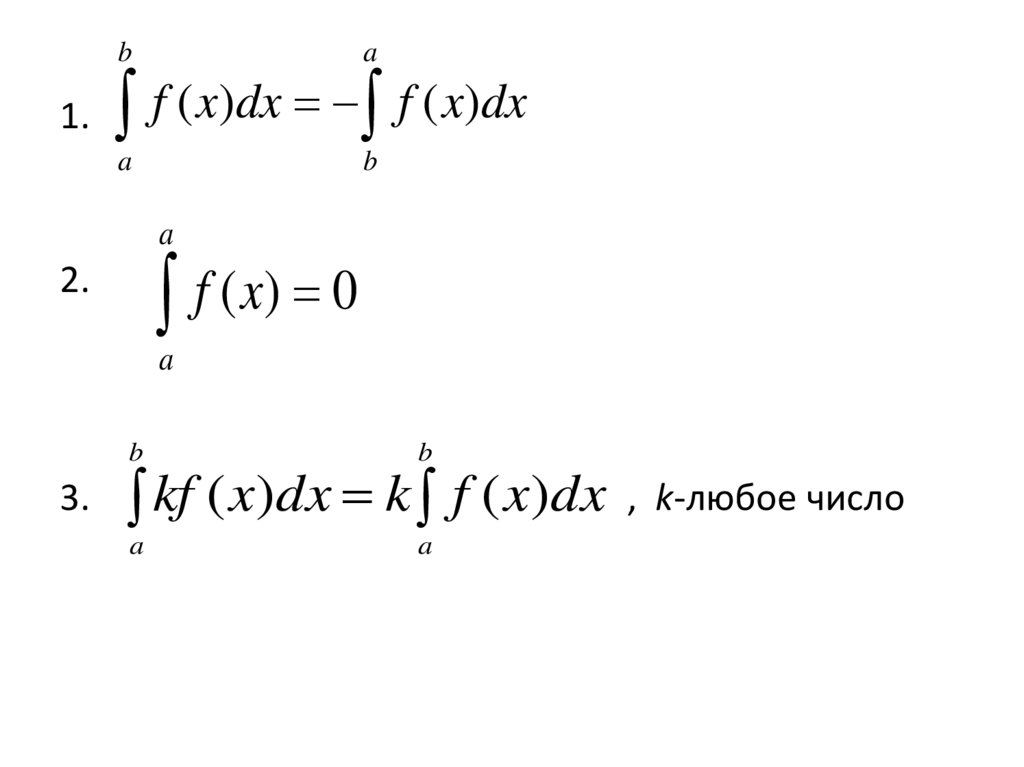
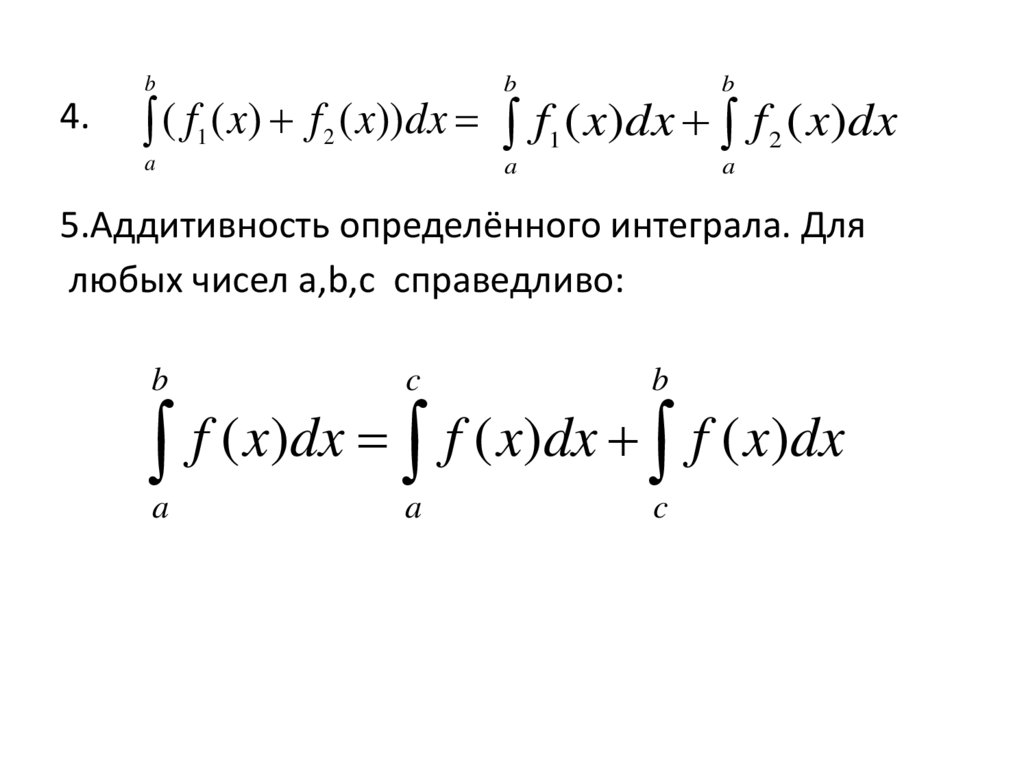





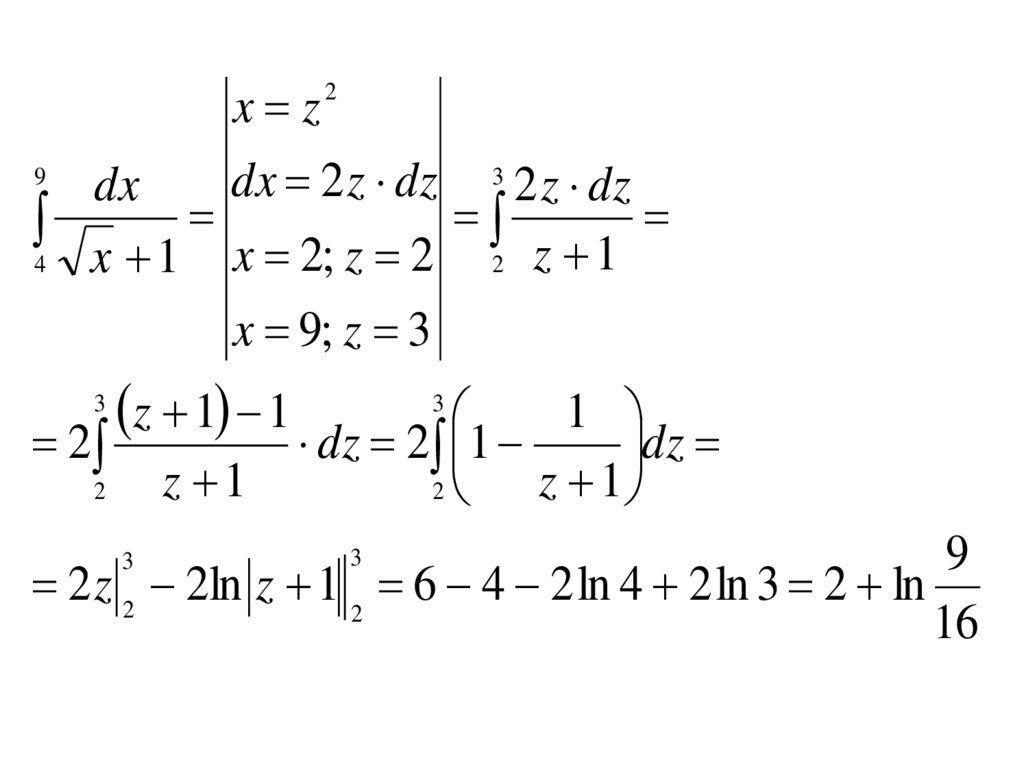

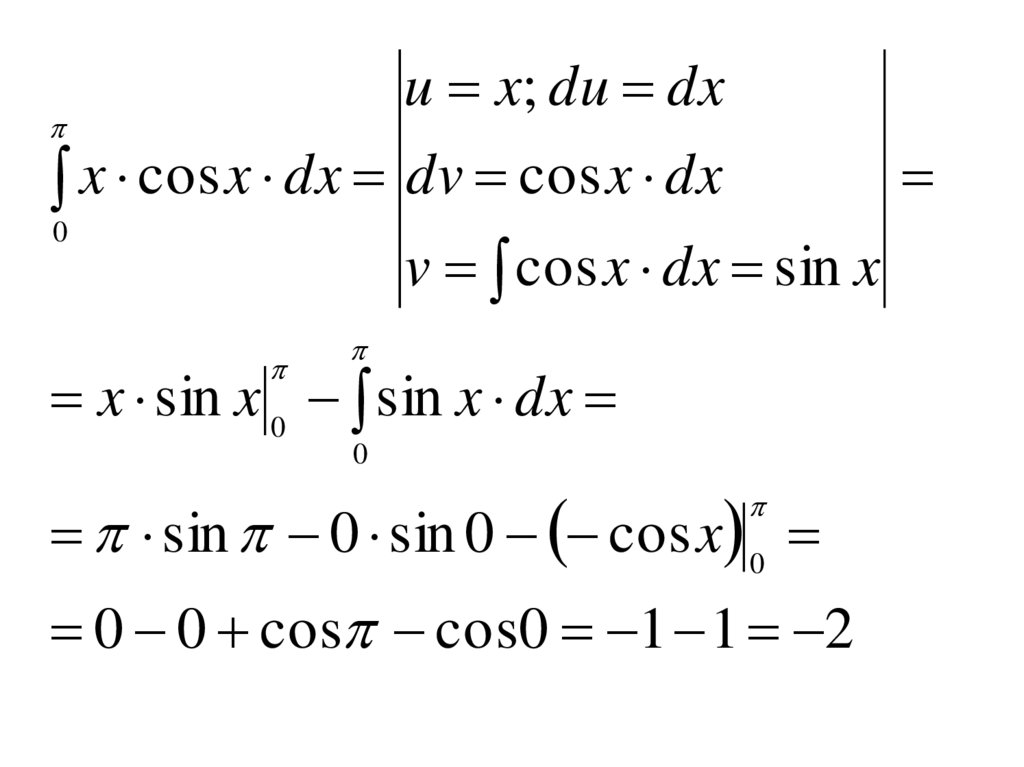


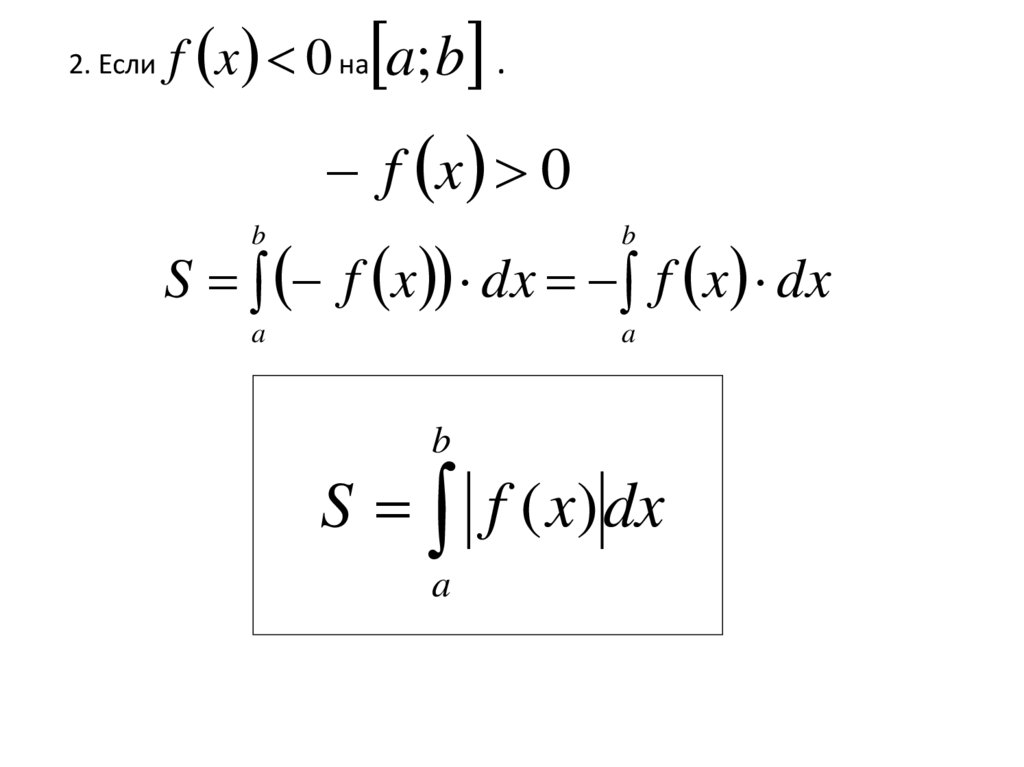













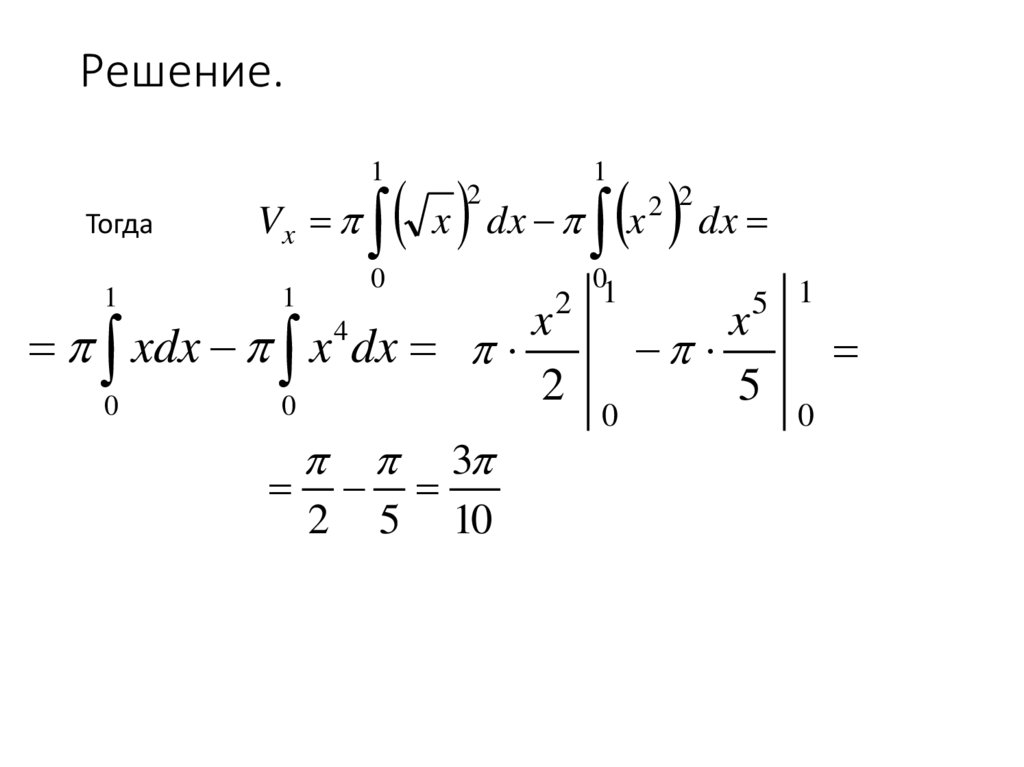
 mathematics
mathematics








