Similar presentations:
Основные геометрические приложения определенного интеграла
1. Основные геометрические приложения определенного интеграла
МГТУ, кафедра Высшей математики ипрограммного обеспечения ЭВМ
Дисциплина «Математический анализ»
Основные геометрические
приложения определенного
интеграла
Авторы: Кацуба В.С., к.ф.-м.н., доцент
Скрябин А.В., ст. преподаватель
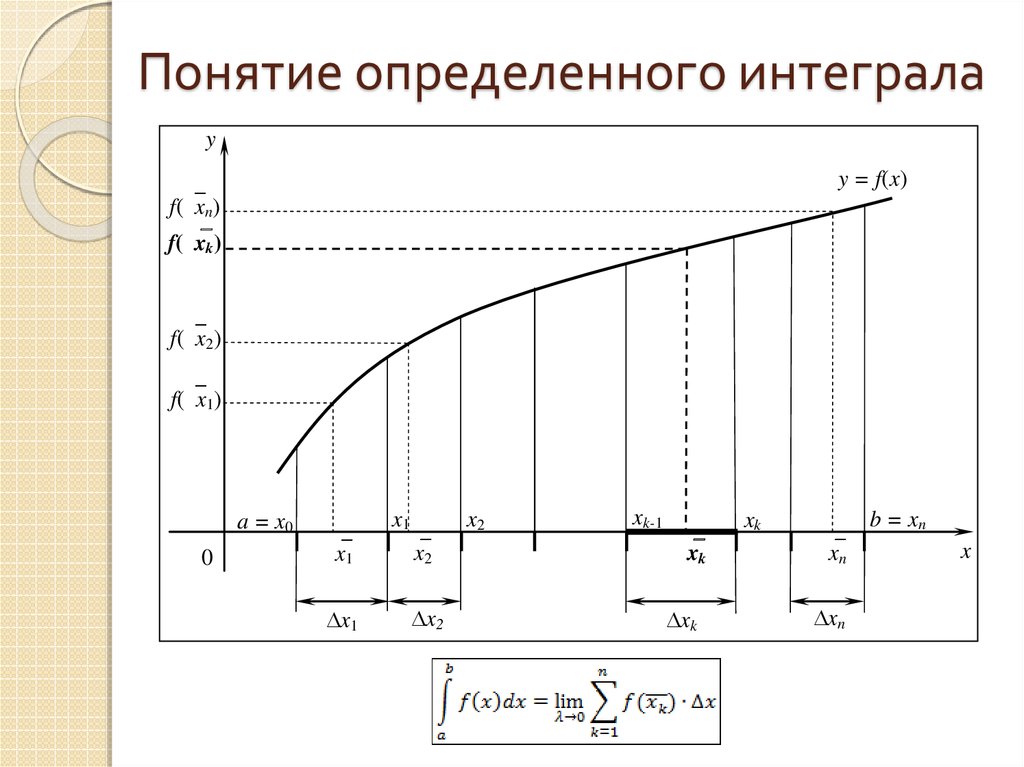
2. Понятие определенного интеграла
yy = f(x)
f( xn)
f( xk)
f( x2)
f( x1)
x1
a = x0
0
x1
x1
x2
x2
x2
xk-1
b = xn
xk
xk
xk
x n
xn
x
3. Понятие определенного интеграла
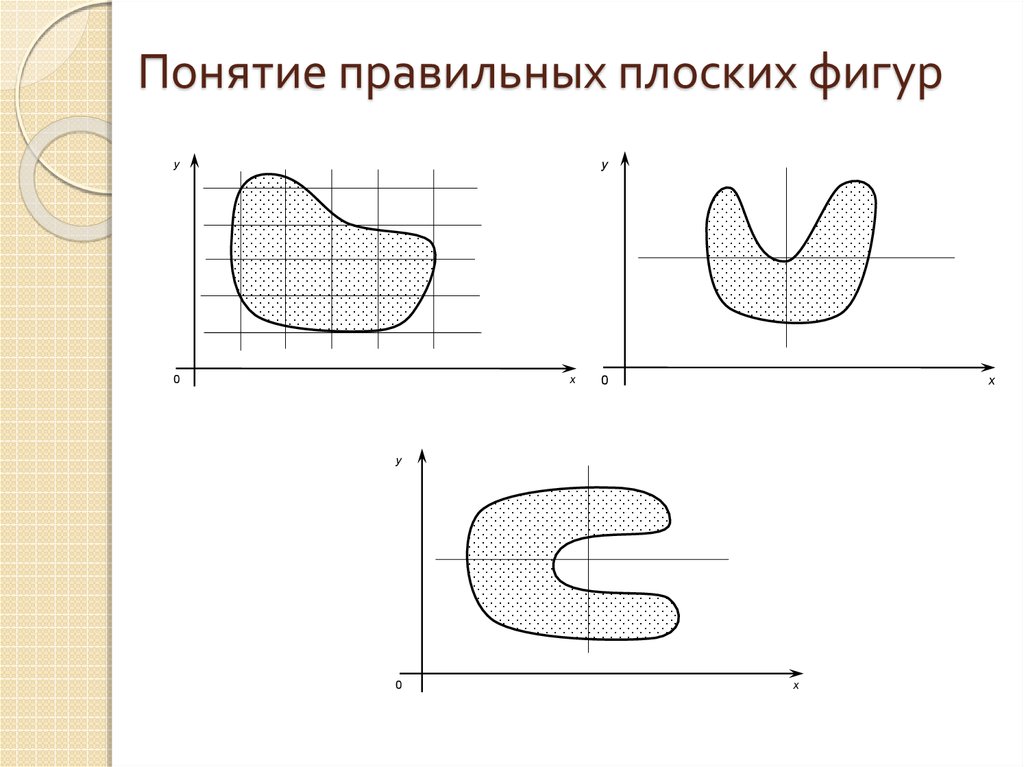
4. Понятие правильных плоских фигур
yy
0
x
0
x
y
0
x
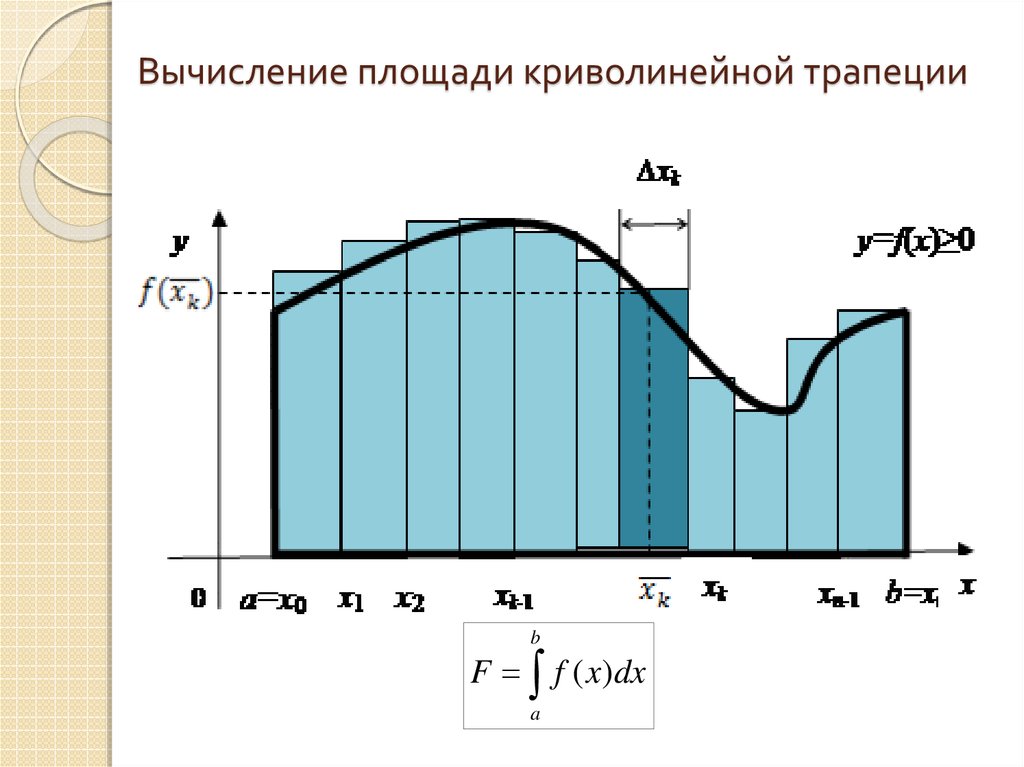
5. Вычисление площади криволинейной трапеции
yy f (x)
b
F f ( x)dx
a
F
a
0
здесь f ( x) 0 x [a; b]
b
x
y f ( x)
y
F
0
a
b
b
a
a
F f ( x)dx f ( x)dx
b
x
F
здесь f ( x) 0 x [a; b]
y f (x)
6. Вычисление площади криволинейной трапеции
bF f ( x)dx
a
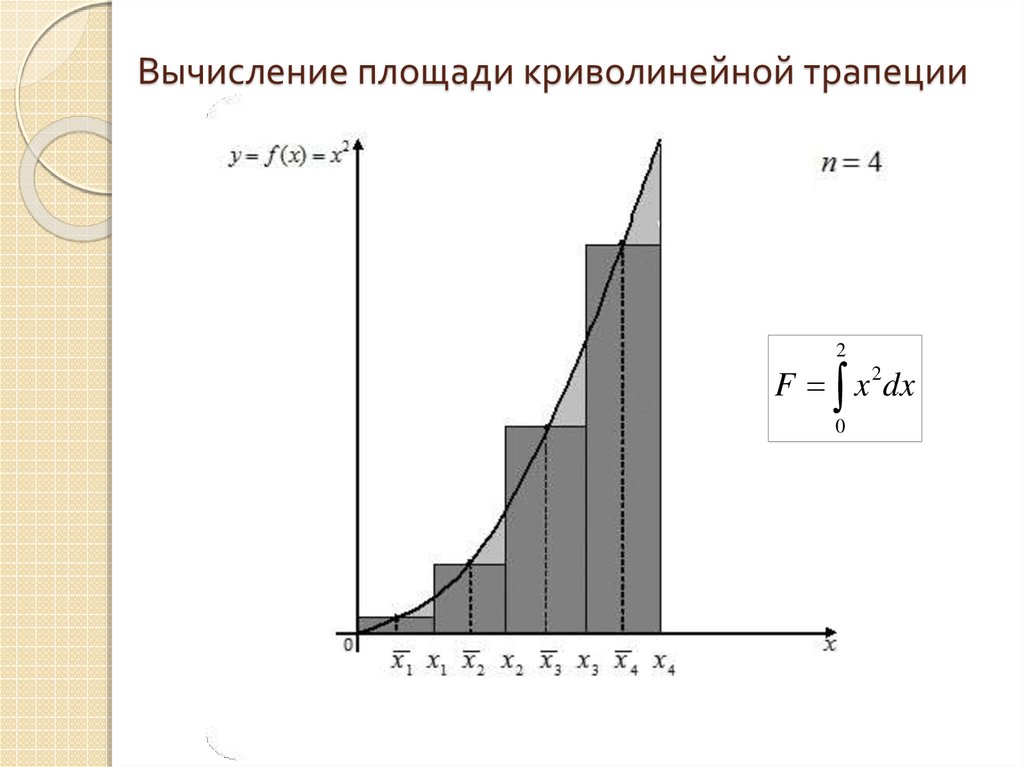
7. Вычисление площади криволинейной трапеции
2F x 2 dx
0
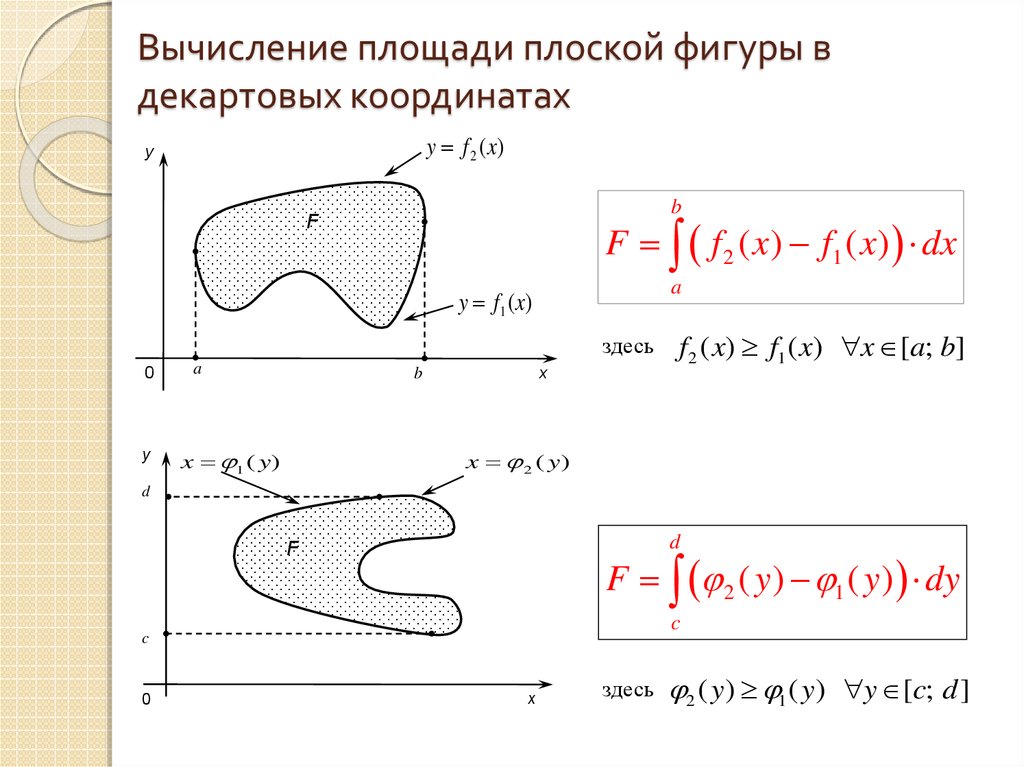
8. Вычисление площади плоской фигуры в декартовых координатах
y f 2 ( x)y
b
F f 2 ( x) f1 ( x ) dx
F
a
y f1 ( x)
здесь
0
y
a
x
b
x 1 ( y)
f 2 ( x) f1 ( x) x [a; b]
x 2 ( y)
d
d
F
F 2 ( y ) 1 ( y ) dy
c
c
0
x
здесь
2 ( y) 1 ( y) y [c; d ]
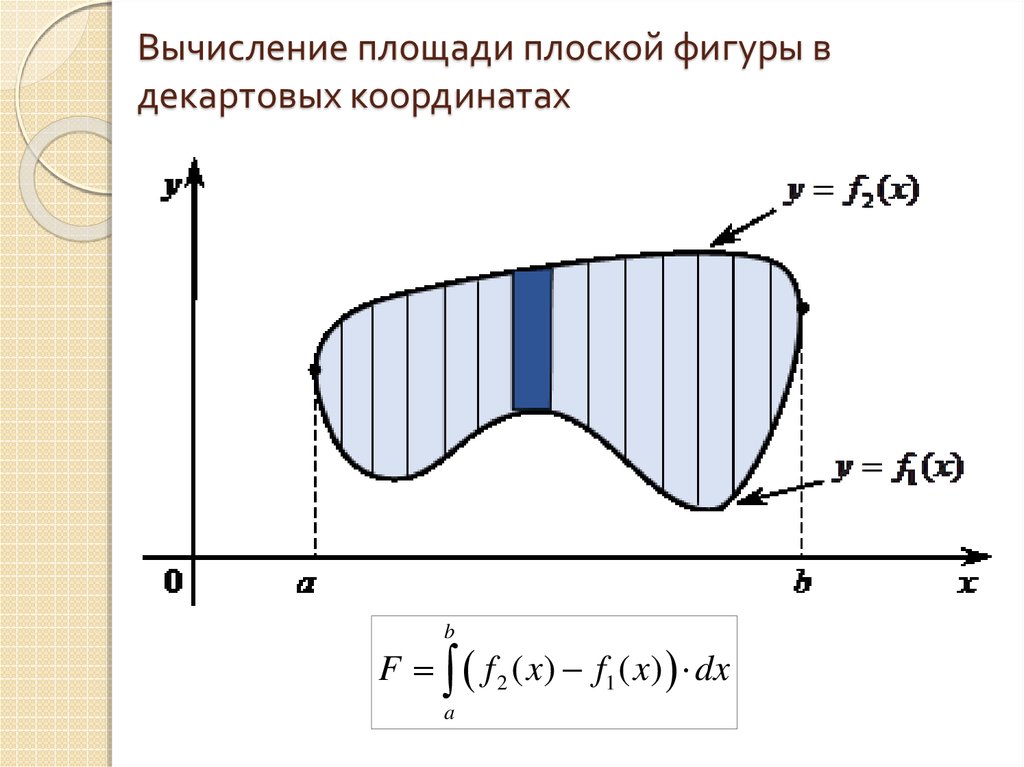
9. Вычисление площади плоской фигуры в декартовых координатах
bF f 2 ( x) f1 ( x ) dx
a
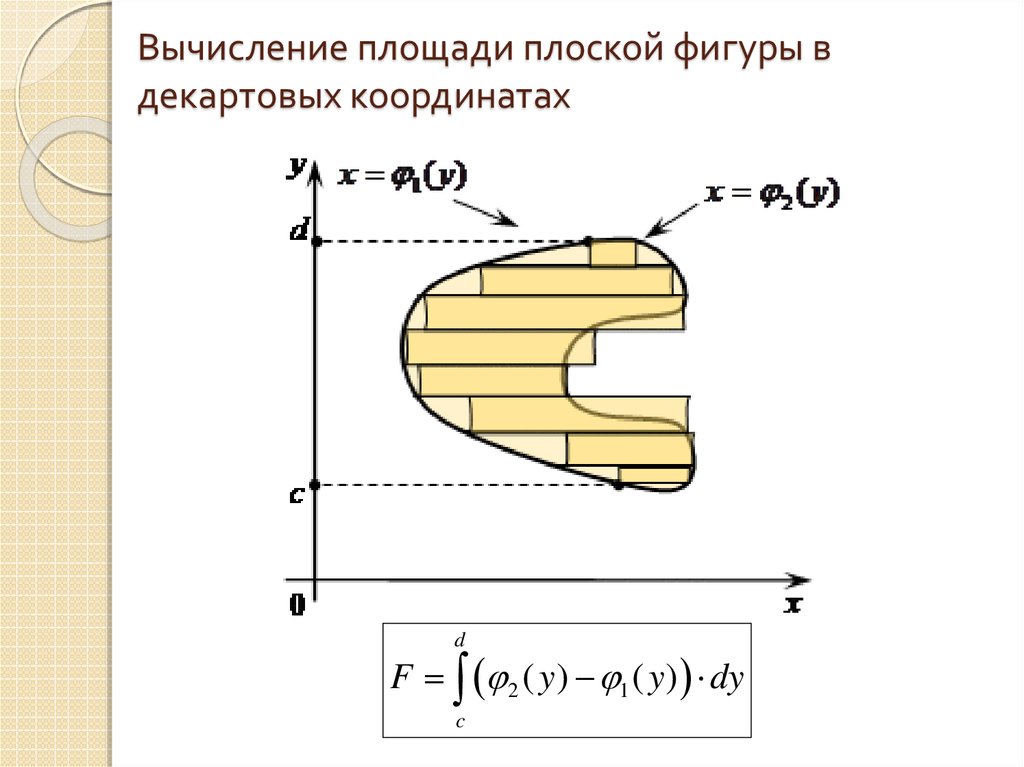
10. Вычисление площади плоской фигуры в декартовых координатах
dF 2 ( y ) 1 ( y ) dy
c
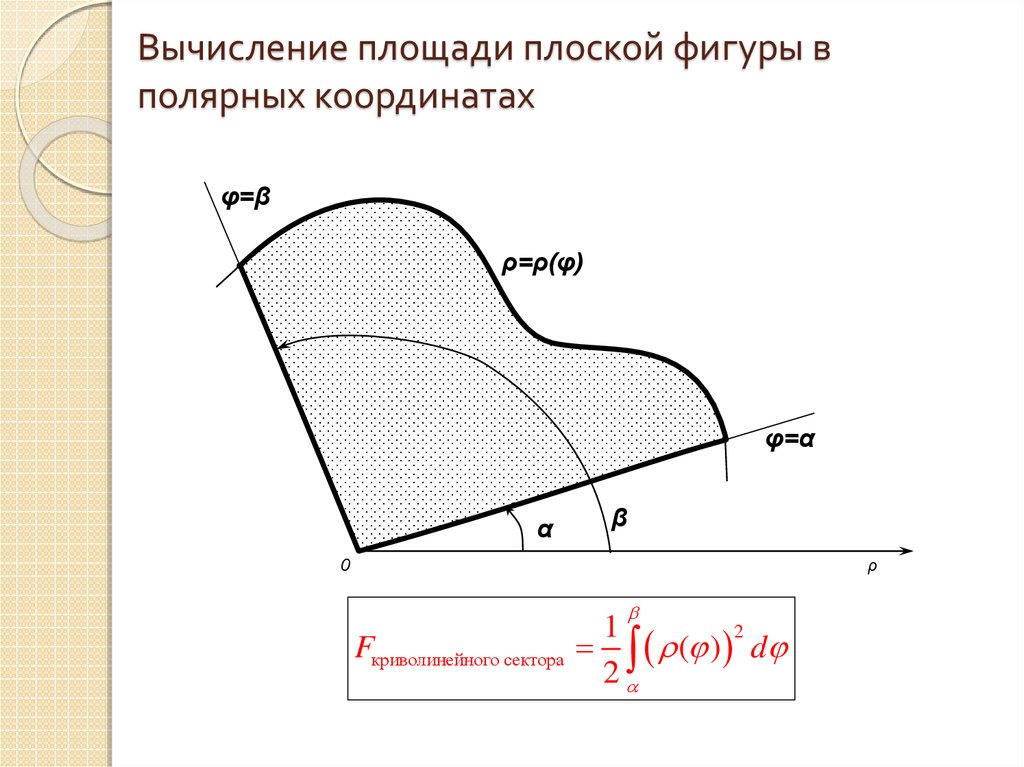
11. Вычисление площади плоской фигуры в полярных координатах
φ=βρ=ρ(φ)
φ=α
α
β
ρ
0
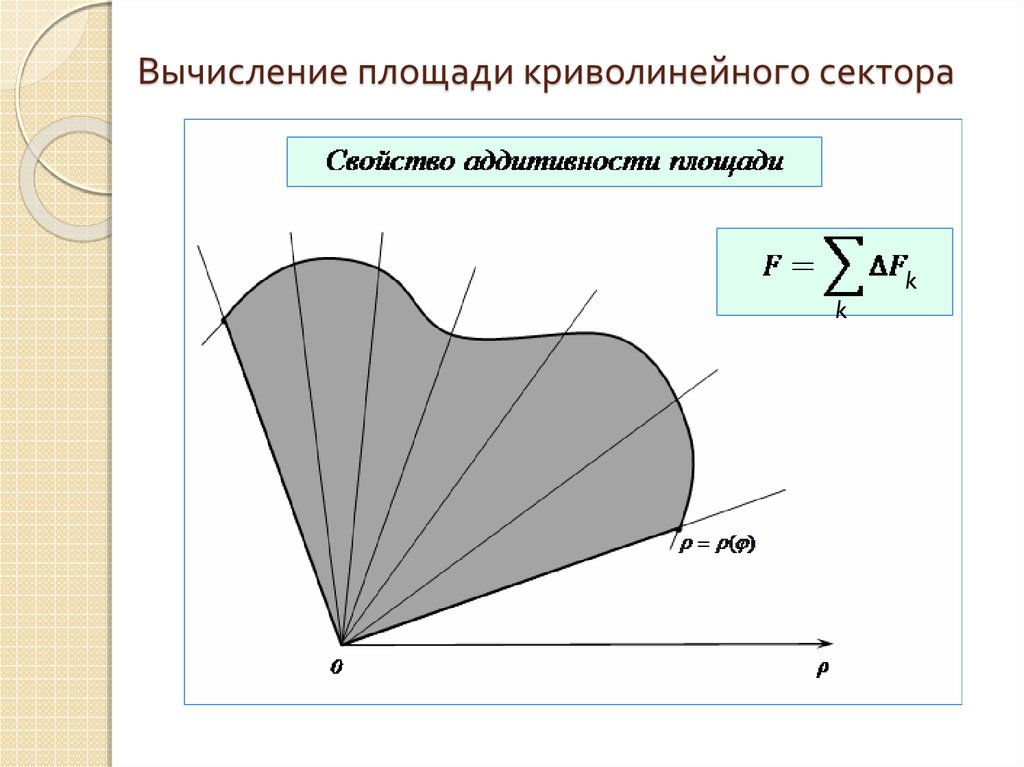
Fкриволинейного сектора
1
2
( ) d
2
12. Вычисление площади криволинейного сектора
kk
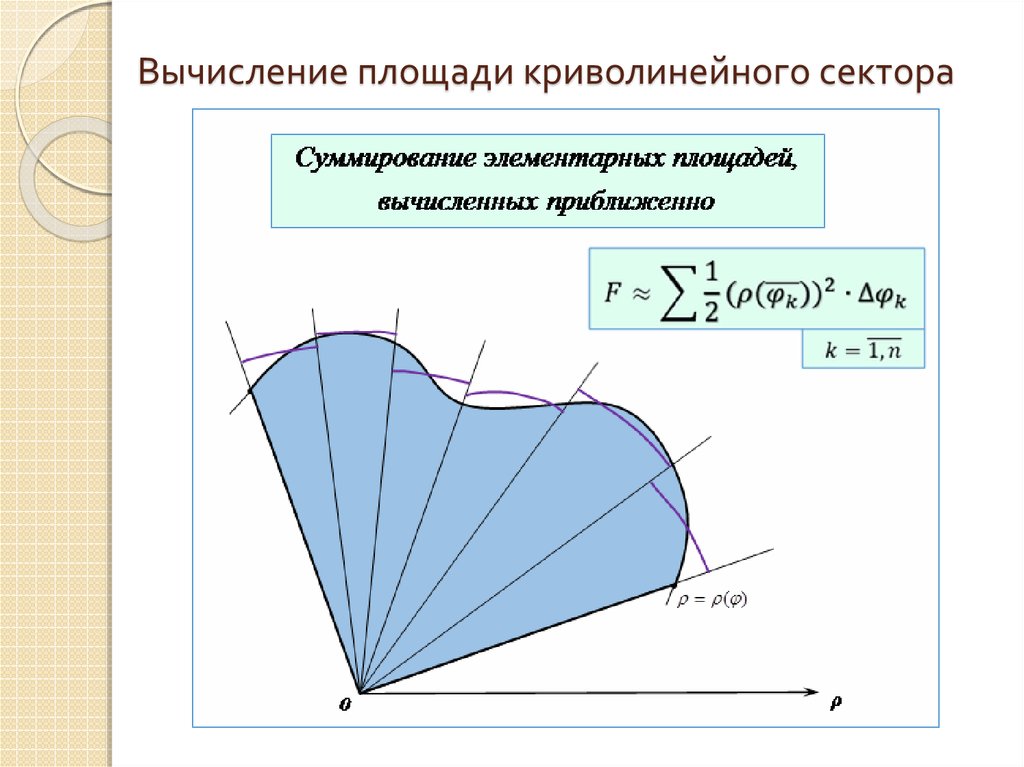
13. Вычисление площади криволинейного сектора
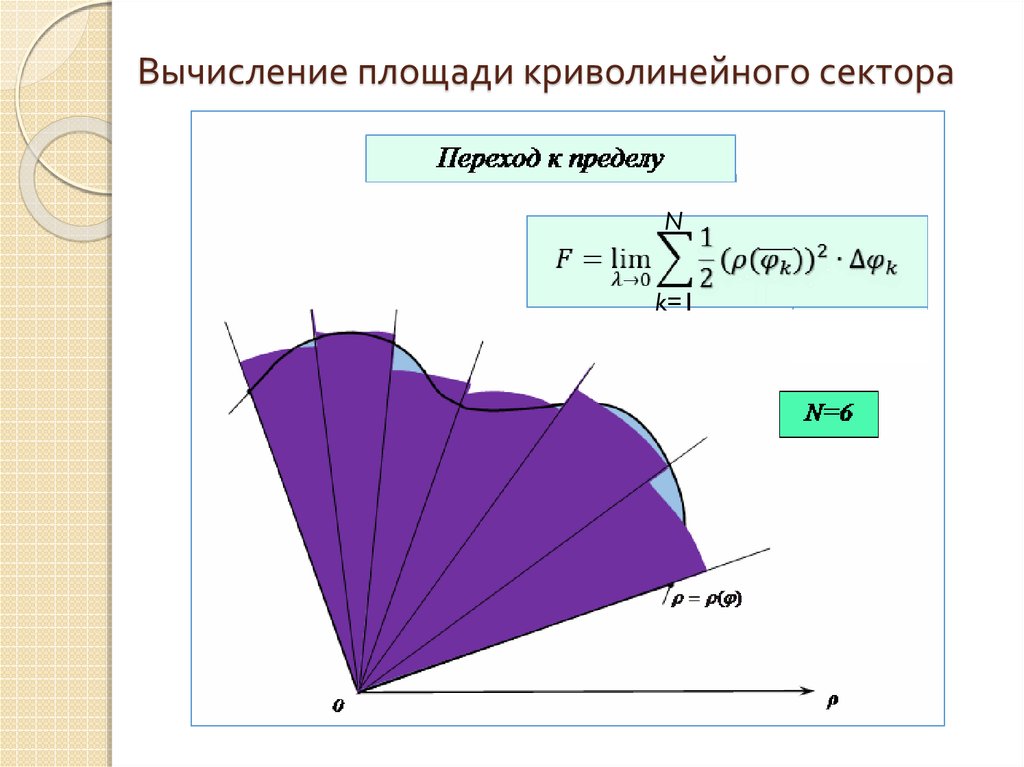
14. Вычисление площади криволинейного сектора
Nk=1
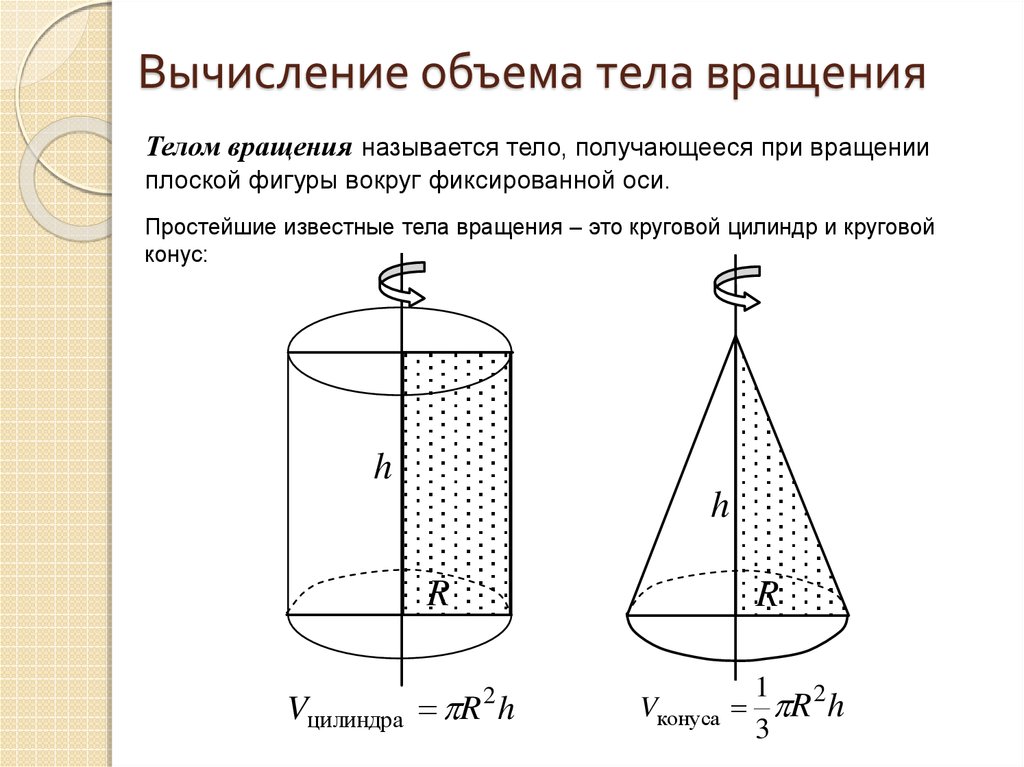
15. Вычисление объема тела вращения
Телом вращения называется тело, получающееся при вращенииплоской фигуры вокруг фиксированной оси.
Простейшие известные тела вращения – это круговой цилиндр и круговой
конус:
h
h
R
R
Vцилиндра R h
2
Vконуса
1 2
R h
3
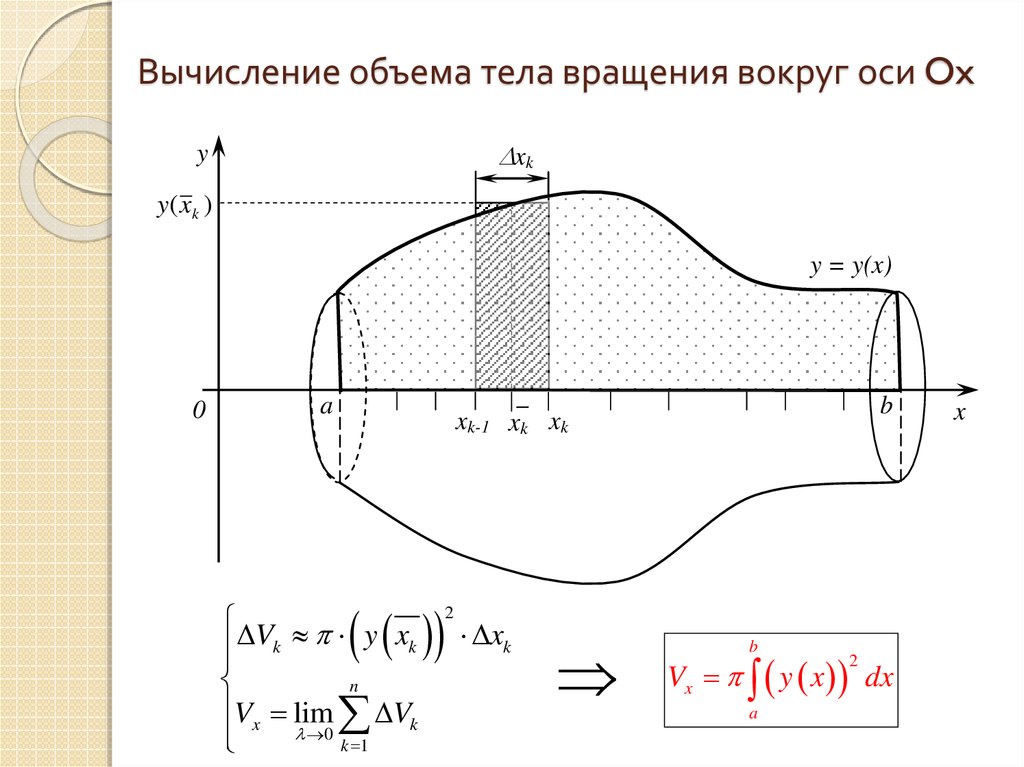
16. Вычисление объема тела вращения вокруг оси Ox
xky
y( xk )
y = y(x)
0
a
b
xk-1 xk xk
x
V y x
k
k
n
Vx lim Vk
0
k 1
2
k
b
Vx y x dx
a
2
x
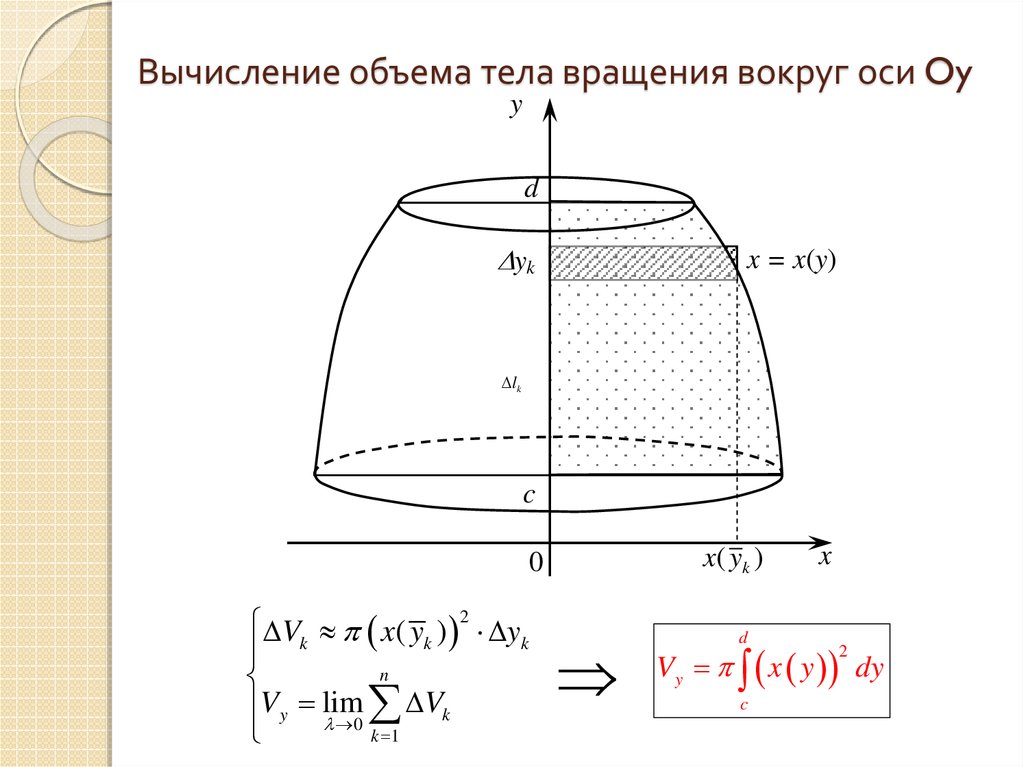
17. Вычисление объема тела вращения вокруг оси Oy
yd
yk
x = x(y)
lk
c
x( yk )
0
Vk x( yk ) 2 yk
n
Vk
Vy lim
0
k 1
d
x
Vy x y dy
c
2
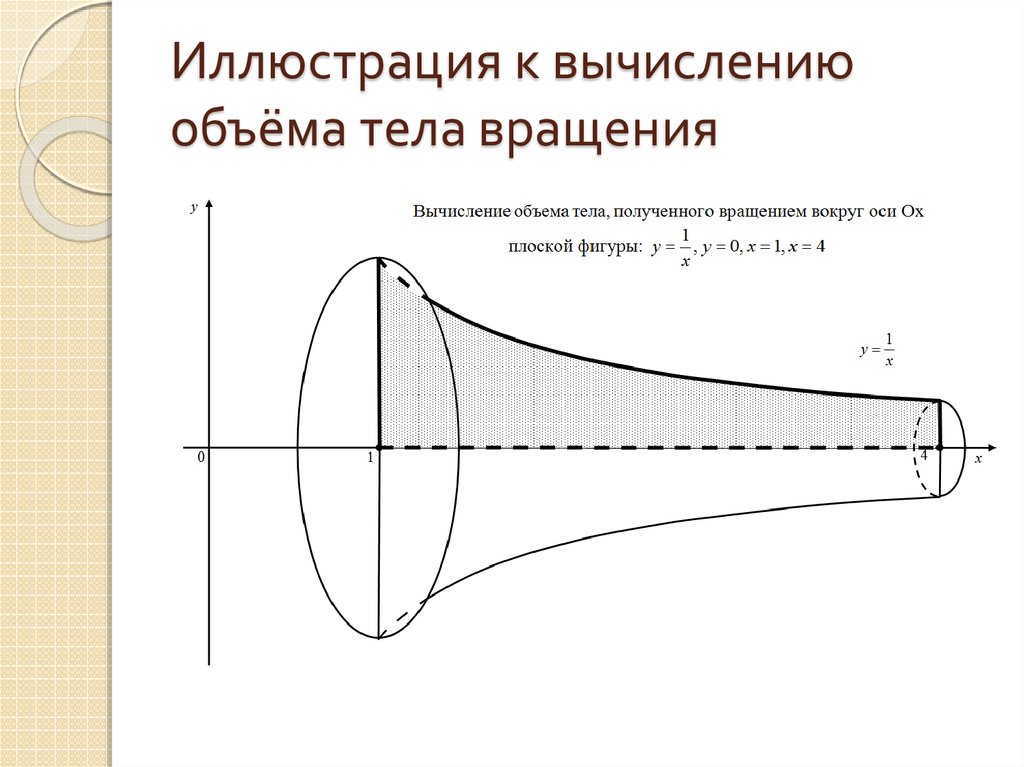
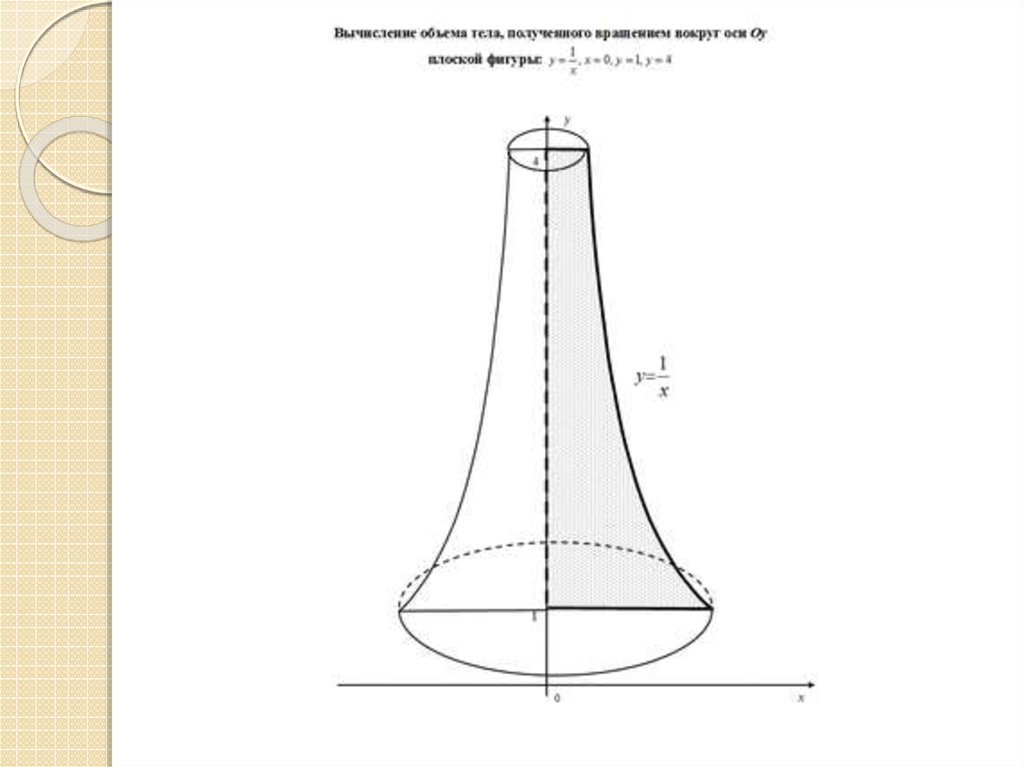
18. Иллюстрация к вычислению объёма тела вращения
19.
20. Вычисление длины дуги плоской кривой
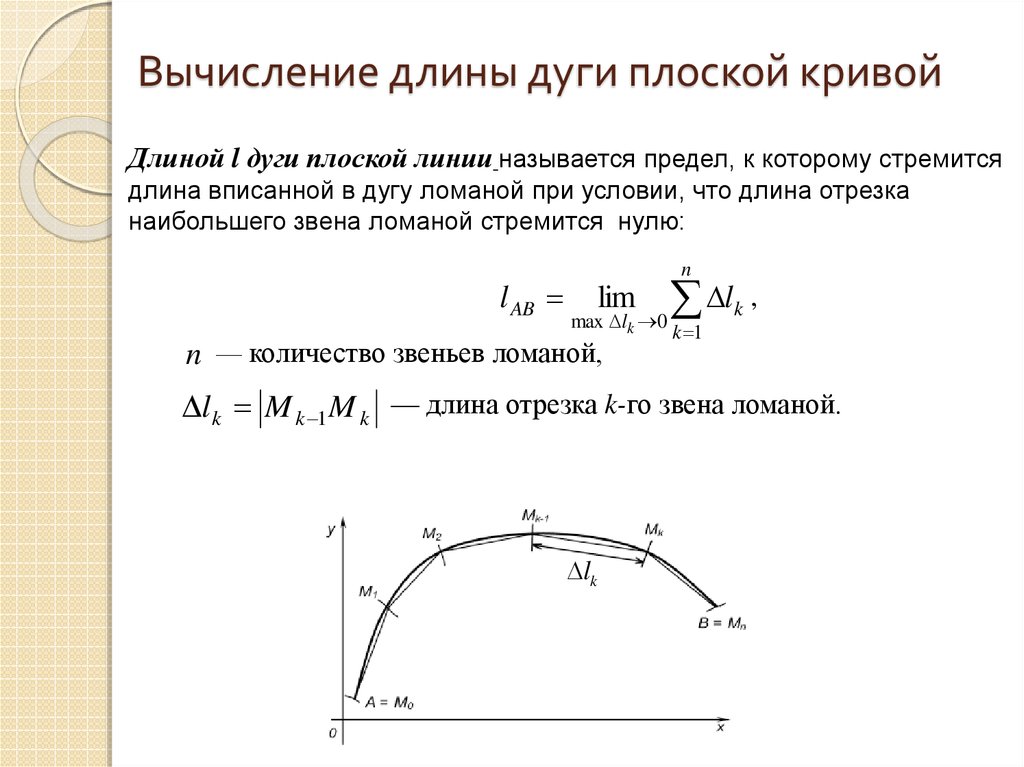
Длиной l дуги плоской линии называется предел, к которому стремитсядлина вписанной в дугу ломаной при условии, что длина отрезка
наибольшего звена ломаной стремится нулю:
l AB
n
lk ,
max l 0
lim
n — количество звеньев ломаной,
k
k 1
lk M k 1M k — длина отрезка k-го звена ломаной.
lk
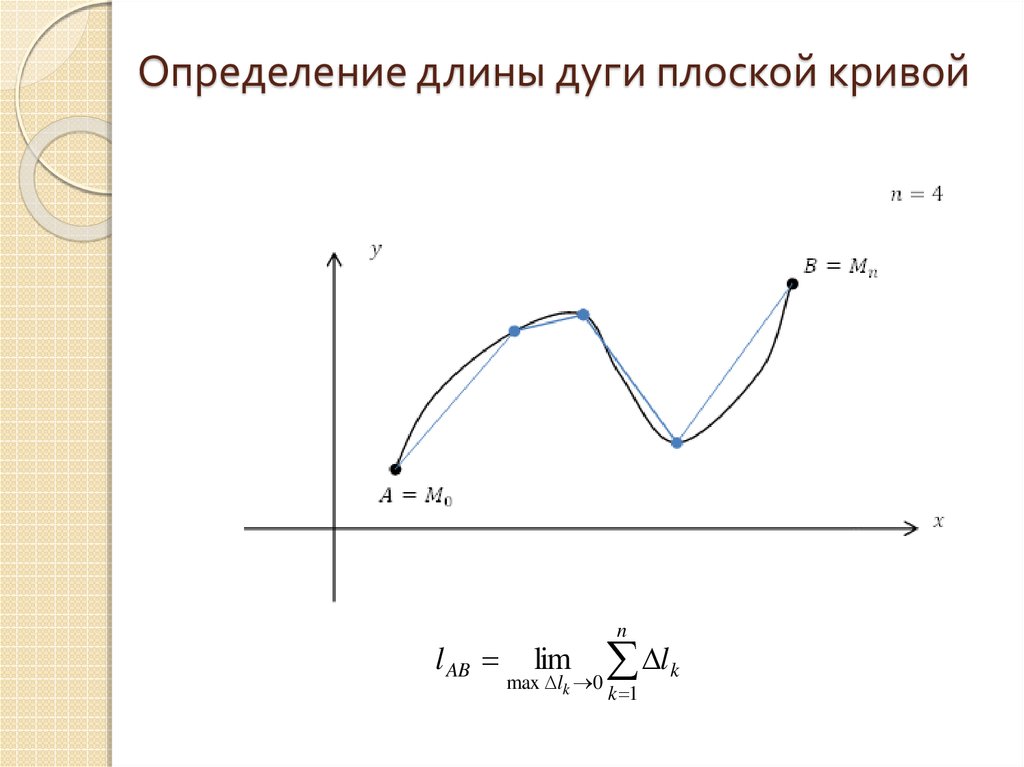
21. Определение длины дуги плоской кривой
l ABn
lk
max l 0
lim
k
k 1
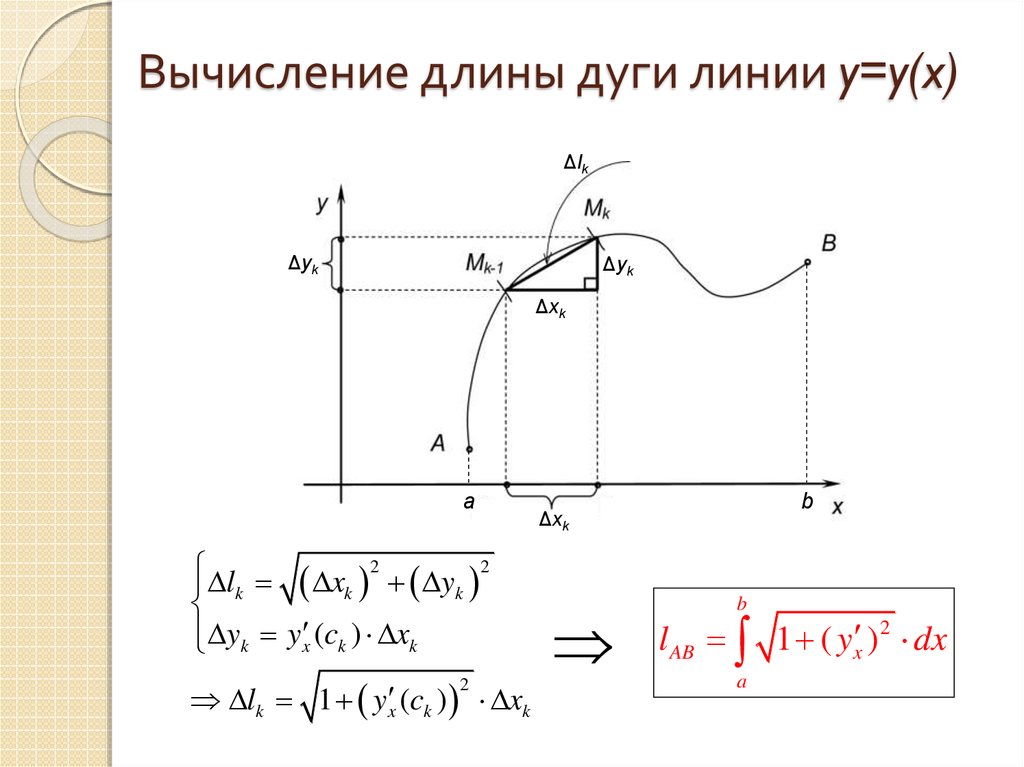
22. Вычисление длины дуги линии y=y(x)
ΔlkΔyk
Δyk
Δxk
a
l x 2 y 2
k
k
k
yk y x (ck ) xk
lk 1 y x (ck ) xk
2
b
Δxk
b
l AB 1 ( y x ) 2 dx
a
23. Формулы для вычисления длины дуги при различных способах ее задания
bЕсли AB: y = y(x), x [a;b], то l AB 1 ( y x ) 2 dx
a
d
Если AB: x = x(y), y [c;d], то l AB ( x y ) 2 1 dy
c
x x(t )
Если AB:
, t [ ; ], то lAB ( xt )2 ( yt )2 dt
y y (t )
Если AB: = ( ), [ ; ], то l AB ( )2 2 d




 mathematics
mathematics








