Приложения определенного интеграла

1. Интегральное исчисление

2. Приложения определенного интеграла

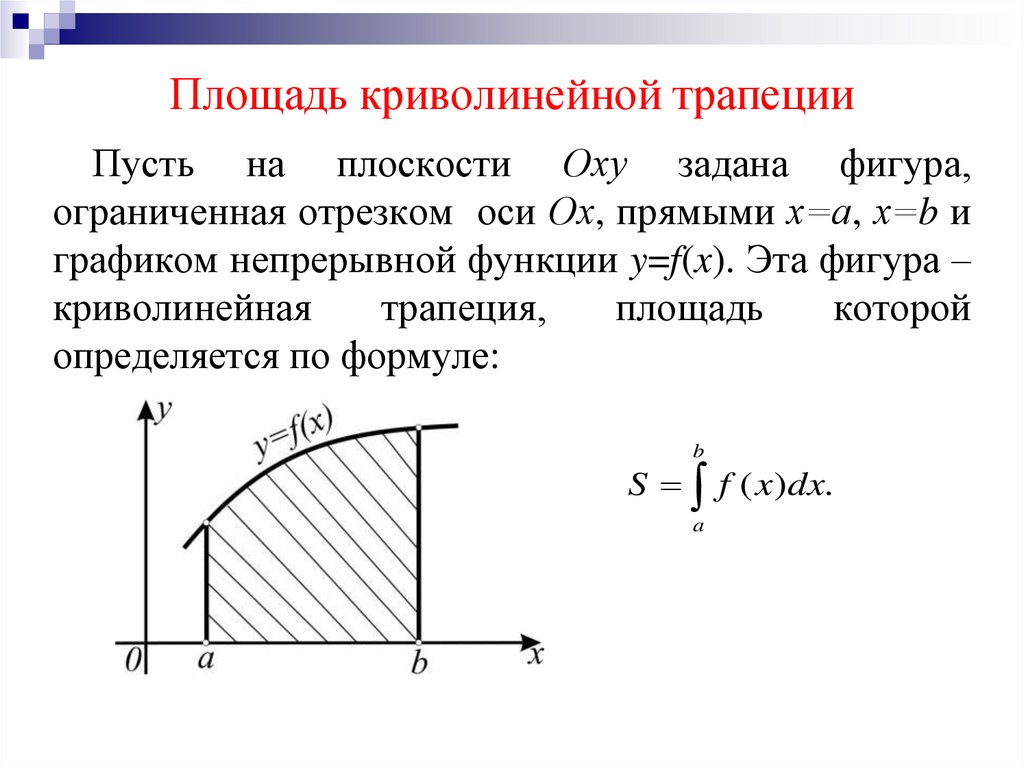
3. Площадь криволинейной трапеции

Пусть на плоскости Оху задана фигура,
ограниченная отрезком оси Ох, прямыми х=а, х=b и
графиком непрерывной функции y=f(x). Эта фигура –
криволинейная
трапеция,
площадь
которой
определяется по формуле:
b
S f ( x)dx.
a

4.

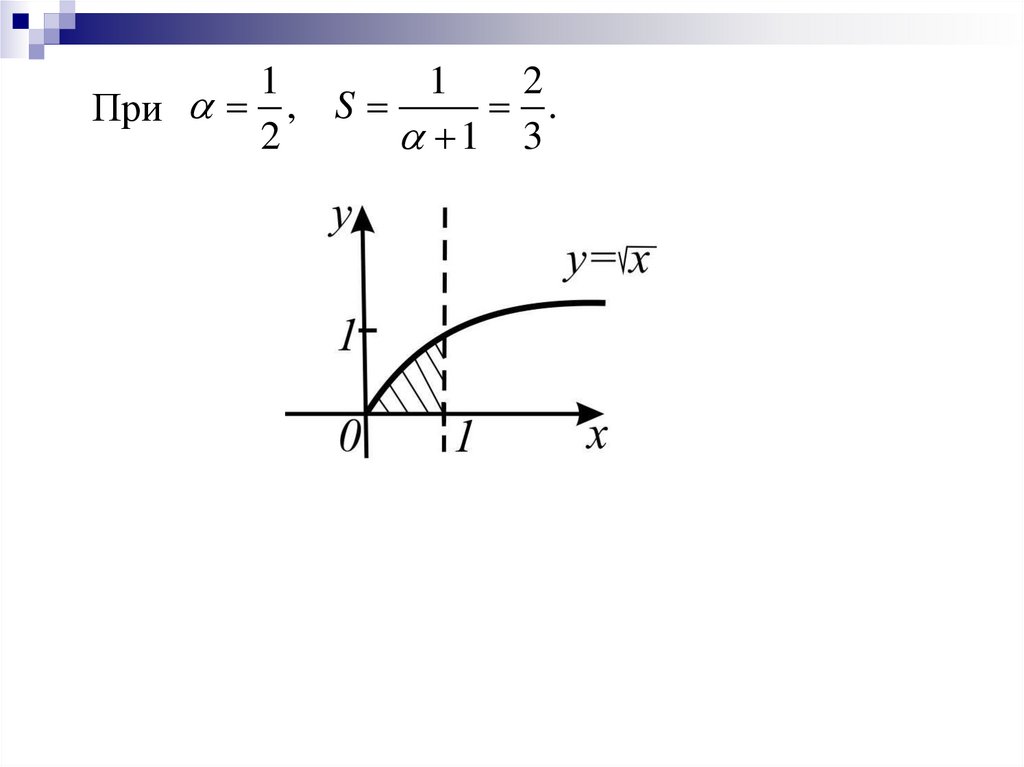
Пример:
Вычислить
площадь
фигуры,
ограниченной графиком функции y x , 0,
прямой х=1 и осью Ох.
Решение:
1
1 1
x
1
По формуле имеем S x dx
.
1 0 1
0
1
1
.
При 2, S
1 3

5.

1
1
2
.
При , S
2
1 3

6.

Если фигура ограничена снизу и сверху
графиками непрерывных функций y f1 ( x)
и
y f 2 ( x) , то площадь криволинейной трапеции
определяется по формуле:
b
b
b
a
a
a
S f 2 ( x)dx f1 ( x)dx f 2 ( x) f1 ( x) dx.

7.

Пример:
Вычислить
площадь
фигуры,
ограниченной графиками функций y x и y 2 x 2 .
Решение:
Найдем абсциссы точек пресечения прямой y x с
параболой y 2 x 2 . Для этого решим систему:
y x;
2
2
x
2
x
,
x
x 2 0, x1 2, x2 1.
2
y 2 x .
1
3
2 1
x x
2
Следовательно, S 2 x x dx 2 x
3 2 2
2
1 1
8
1 9
2 4 2 5 .
3 2
3
2 2

8.

Если функция задана
параметрическими
уравнениями x (t ), y (t ), t , причем
( ) a, ( ) b , то площадь криволинейной
трапеции определяется по формуле:
S (t ) (t ) dt.

9.

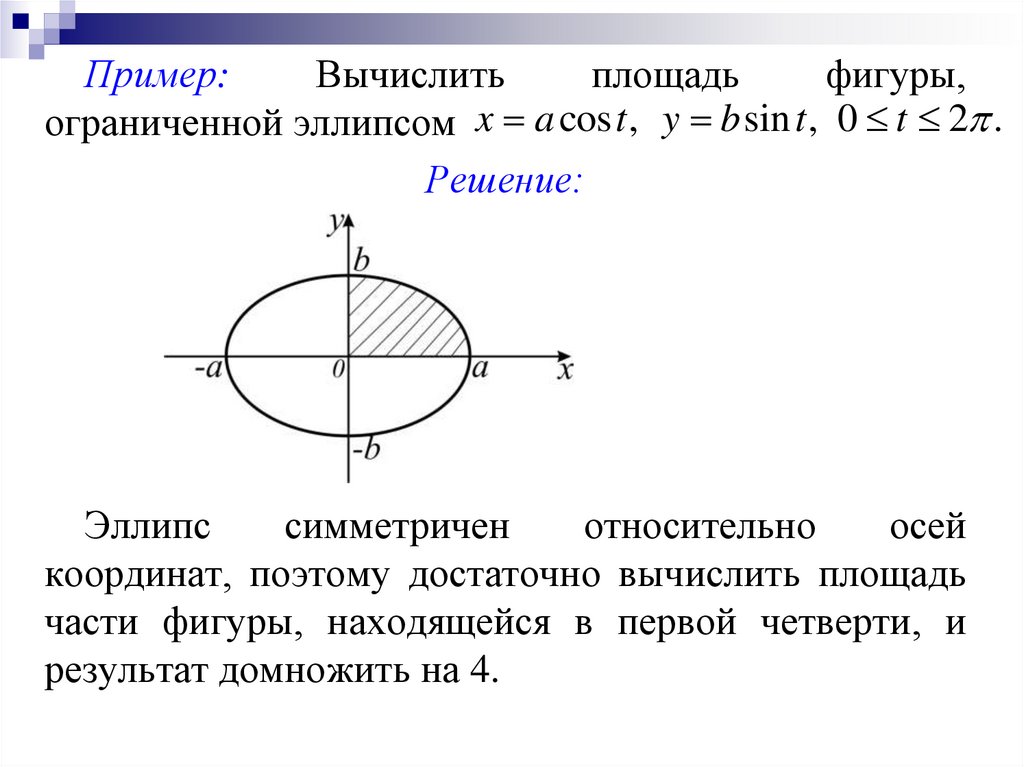
Пример:
Вычислить
площадь
фигуры,
ограниченной эллипсом x a cos t , y b sin t , 0 t 2 .
Решение:
Эллипс
симметричен
относительно
осей
координат, поэтому достаточно вычислить площадь
части фигуры, находящейся в первой четверти, и
результат домножить на 4.

10.

В первой четверти 0 t
2
.
1 cos 2t
2
S b sin t a cos t dt 4ab sin tdt 4ab
dt
2
0
0
2
2
2
1
1
2
2ab dt cos 2td (2t ) 2ab t sin 2t
20
2
0
0
1
1
2ab sin 0 sin 0 ab.
2
2 2
В частности, если a b r то получаем формулу
площади круга S r 2 .
0
2
2

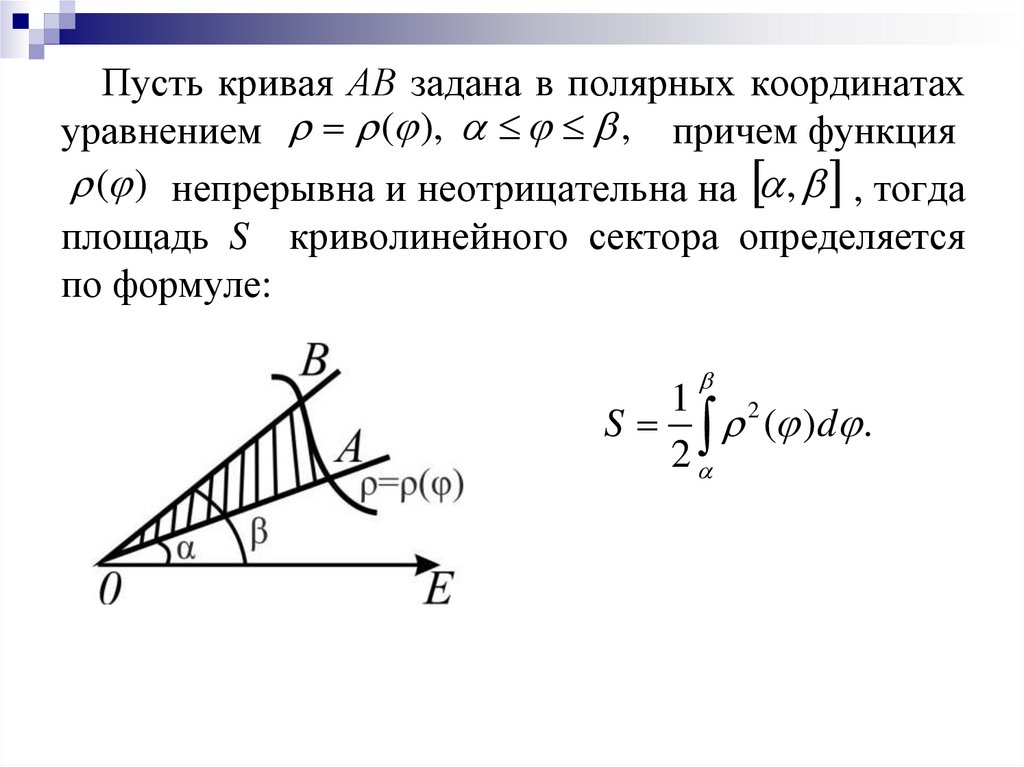
11. Площадь криволинейного сектора

Определение: Плоскую фигуру, ограниченную
кривой АВ, заданной в полярной системе координат
уравнением ( )
и двумя лучами, которые
образуют с полярной осью углы и , называют
криволинейным сектором.

12.

Пусть кривая АВ задана в полярных координатах
уравнением ( ), , причем функция
( ) непрерывна и неотрицательна на , , тогда
площадь S криволинейного сектора определяется
по формуле:
1 2
S ( )d .
2

13.

Пример:
Вычислить
площадь
фигуры,
ограниченной полярной осью и первым витком
спирали Архимеда a , a 0.
Решение:
При изменении φ от 0 до
2π полярный радиус
описывает кривую,
ограниченную криволинейным
сектором, поэтому имеем:
2
3 2
1
1 2
a2
4 3 2
2
3
S a d a
(2 ) 0 a .
20
2
3 0
6
3

14. Длина дуги кривой

Пусть плоская кривая АВ задана уравнением
y f ( x ), a x b, где f(x) непрерывная функция
на отрезке [a; b].
Разобьем кривую АВ на n произвольных частей
точками А=М0, М1, …, Мn-1,Мn=B.

15.

Соединив соседние точки хордами, получим
некоторую вписанную в кривую АВ ломаную.
Через li обозначим длину одного звена Mi-1Mi
ломаной.
Определение: Длиной L дуги АВ называется тот
предел, к которому стремится дуга вписанной
ломаной, когда длина ее наибольшего звена
стремится к нулю:
L lim
max li 0
n
l .
i 1
i

16.

Если функция f ( x) непрерывна вместе со своей
производной f ( x) на a; b , то длина L дуги АВ
выражается формулой:
b
L 1 f ( x) dx.
2
a

17.

Пример: Вычислить длину дуги полукубической
параболы y 2 x3 , если 0 x 4 .
3
Решение:

18.

3
2
1
3
9
2
3
2
y x x , y x , y x.
2
4
Так как на данном отрезке функция имеет две
симметричные и одинаковые по длине ветви, то
b
4
3
9
L 1 f ( x) dx 2 1 x dx
4
a
0
2
4
3
4
3
1
2
1
2
8 9 9 8 9 9
1 x d x 1 x d x 1
9 0 4 4 9 0 4 4
9
1 x
8 4
3
9
2
3
2
4
3
0
16
112
8 1
.
27
27

19.

Если кривая АВ задана параметрическими
уравнениями x (t )
, то длина дуги
; t
y (t )
кривой определяется по формуле:
2
(t )
L 1 f ( x) dx 1
(t )dt
(t )
a
b
2
Или L 2 (t ) 2 (t )dt.

20.

Пример: Вычислить длину одной арки циклоиды:
x a(t sin t );
0 t 2 .
y a(1 cos t ).
Решение:
x a(t sin t ) a(1 cos t ),
x a 2 (1 cos t )2.
y a(1 cos t ) a sin t ,
2
2
y a 2 sin 2 t.

21.

Итак,
2
0
L 2 (t ) 2 (t )dt a 2 (1 cos t ) 2 a 2 sin 2 tdt
2
2
a 1 2cos t cos t sin tdt a 2 2cos tdt
2
2
0
0
2
2
a 2(1 cos t )dt a
0
0
2
2
t
t
2 2sin dt 2a sin dt
2
2
0
2
2
t t
t
2a 2 sin d 4a cos
4a(cos cos0)
2 2
2 0
0
4a( 1 1) 8a.

22.

Если кривая АВ задана в полярных координатах
уравнением ( ), , где ( ) имеет
непрерывную производную ( ) на отрезке , и
точкам А и В соответствуют значения , равные и
, то длина дуги кривой определяется по формуле:
L 2 ( ) 2 ( )d .

23.

Пример: Вычислить длину кардиоиды:
a(1 cos ), 0 t 2 .
Решение:
a(1 cos ) a sin ,
2
0
a 2 sin 2 .
2
L 2 2 d a 2 (1 cos ) 2 a 2 sin 2 d 8a.

24. Объем тела вращения

Если функция f ( x) непрерывна и неотрицательна
на отрезке a; b . Тогда тело, которое образуется
вращением вокруг оси Ох криволинейной трапеции,
ограниченной сверху графиком функции y f ( x ) ,
имеет объем:
b
V f 2 ( x)dx
a
b
или
V y 2 dx.
a

25.

Пример: Вычислить объем тела, образованного
вращением фигуры, ограниченной линиями xy 4,
x 1, x 4, y 0 вокруг оси Ох.
Решение:
4
xy 4 y
x
b
4
4
1 4
16
x
2
V y dx 2 dx 16 x dx 16
x
1 1
a
1
1
4
16
16 16
16 4 12 .
x 1
4
1
2

26.

Если функция f ( x) непрерывна и неотрицательна
на отрезке c; d . Тогда тело, которое образуется
вращением вокруг оси Оу криволинейной трапеции,
ограниченной графиком функции y f ( x ) , имеет
объем:
d
V x 2 dy.
c
где x ( y ) обратная
функция для y f ( x).

27.

Пример: Вычислить объем тела, образованного
2
y
4 x,
вращением фигуры, ограниченной линиями
x 0 вокруг оси Оу.
Решение:
y2 4 x x 4 y2
d
2
V x dy 4 y dy
2
c
2
2 2
2
2
V 2 4 y dx 2 16 8 y 2 y 4 dy
0
2 2
0
y
y
64 32 512
2 16 y 8 2 32
.
3
5 0
3
5
15
3
5
2

28. Площадь поверхности вращения

Если функция f ( x) непрерывна и неотрицательна
вместе со своей первой производной f ( x)
на
отрезке a; b , тогда поверхность, образованная
вращением графика этой функции вокруг оси Ох,
имеет площадь Р, которая может быть вычислена по
формуле:
b
P 2 f ( x) 1 f 2 ( x)dx.
a

29.

Пример: Определить площадь поверхности,
образованной вращением кривой x 2 y 2 R 2 вокруг
оси Ох.
Решение:
x2 y 2 R2
y
1
2 R x
2
b
R
a
R
P 2 f ( x) 1 f 2 ( x)dx 2
R
2
R
y R2 x2
2
( 2 x)
x
R x
2
2
2
x
R2 x2 1 2
dx
2
R x
2
2
2
R
x
x
2
R2 x2
dx
2
Rx
4
R
.
2
2
R x
R
R

30.

Если линия задана параметрическими уравнениями
x (t );
t ,
y (t ).
то площадь поверхности, образованная вращением
графика этой функции вокруг оси Ох, равна:
b
P 2 (t ) 2 (t ) 2 (t )dt.
a

31.

Пример: Определить площадь поверхности,
образованной вращением вокруг оси Ох дуги кривой:
x a cos3 t ;
0 t .
3
2
y a sin t.
Решение:
x a cos t a 3cos 2 t ( sin t ),
y a sin t a 3sin t cos t ), y 9a sin t cos t.
3
3
2
2
4
2
x
9
a
cos
t
sin
t.
2
2
2
4
2
2 (t ) 2 (t ) 9a 2 cos 4 t sin 2 t 9a 2 sin 4 t cos 2 t
9a 2 cos 2 t sin 2 t (cos 2 t sin 2 t ) 3a cos t sin t.

32.

b
P 2 (t ) 2 (t ) 2 (t )dt
a
2
2
0
0
2 a sin 3 t 3a sin t cos tdt 6 a 2 sin 4 t cos tdt
z sin t ,
t 0 z 0
1
5 1
z
6 a z dz 6 a
5 0
dz cos tdt , t z 1
0
2
2
6 2
a .
5
6 2
Следовательно, P a .
5
4
2

33. Вычисление работы

Под действием некоторой силы F материальная
точка М движется по прямой OS, причем
направление силы совпадает с направлением
движения. Тогда работа, произведенная силой F
при перемещении точки М из положения S a в
положение S b определяется по формуле:
b
A F ( S )dS .
a

34. Координаты центра масс плоской фигуры

Если фигура ограничена линиями y f1 ( x) и
y f 2 ( x), x a, x b представляет
собой
материальную плоскую фигуру.
Поверхностную плотность (массу единицы
площади поверхности) будем считать постоянной и
равной для всех частей фигуры, тогда координаты
центра масс плоской фигуры равны:
b
x f ( x) f ( x) dx
2
1
xc ab
f ( x) f ( x) dx
2
a
b
1
, yc
1
2
2
f
(
x
)
f
2
1 ( x ) dx
2a
b
f ( x) f ( x) dx
2
a
1
.