Приложения определенного интеграла. Геометрические приложения определенного интеграла

1.

Приложения
определенного интеграла
Геометрические приложения
определенного интеграла

2.

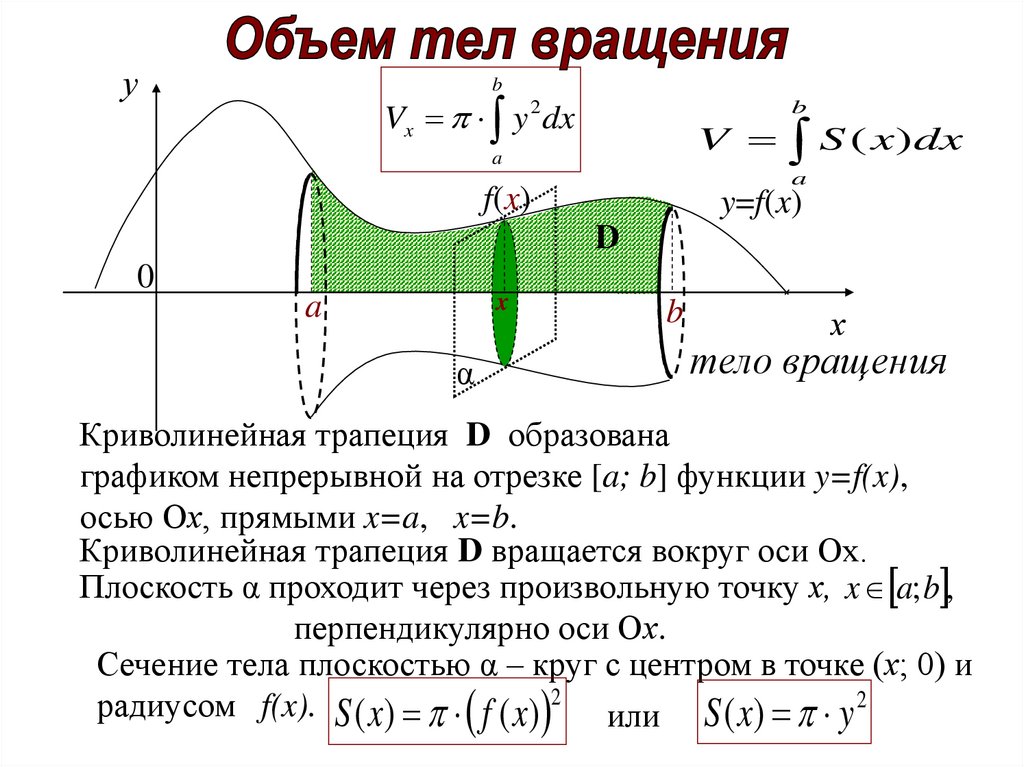
у
b
Vx y 2 dx
b
V S ( x ) dx
a
a
f(x)
y=f(x)
D
0
x
a
α
b
х
тело вращения
Криволинейная трапеция D образована
графиком непрерывной на отрезке [a; b] функции y=f(x),
осью Ох, прямыми x=a, x=b.
Криволинейная трапеция D вращается вокруг оси Ох.
Плоскость α проходит через произвольную точку х, x a;b ,
перпендикулярно оси Ох.
Сечение тела плоскостью α – круг с центром в точке (х; 0) и
радиусом f(x). S ( x) f ( x) 2 или S ( x) y 2

3.

образованных, вращением фигуры, ограниченной графиком
непрерывной функции х=g(у)≥0, прямыми y=с, y=d (c<d) и
осью Оу, вокруг оси Оу.
х=g(у)
у
d
d
Vy x dy
2
c
с
0
х

4.

образованных вращением криволинейной трапеции,
ограниченной графиком непрерывной функции у=f(х)≥0,
прямыми x=a, x=b (a<b) и осью Оx, вокруг оси Оу.
у
b
Vy 2 xydx
a
0
a
x x+Δx b
х

5.

полученных при вращении сектора, ограниченного дугой
кривой ρ=ρ(φ) и двумя полярными радиусами φ=α, φ=β (α<β),
вокруг полярной оси.
2
V 3 sin d
3
образованных вращением криволинейной трапеции,
ограниченной графиками непрерывных функций y=f(x) и y=h(x)
(f(x) ≤ h(x)),прямыми х=а, х=b (a<b) и осью Оу, вокруг оси Оx.
Vx h 2 ( x) f 2 ( x) dx
b
a
образованных вращением криволинейной трапеции,
ограниченной графиками непрерывных функций y=f(x) и y=h(x)
(f(x) ≤ h(x)),прямыми х=а, х=b (a<b) и осью Оу, вокруг оси Оу.
b
Vy 2 x h( x) f ( x) dx
a

6.

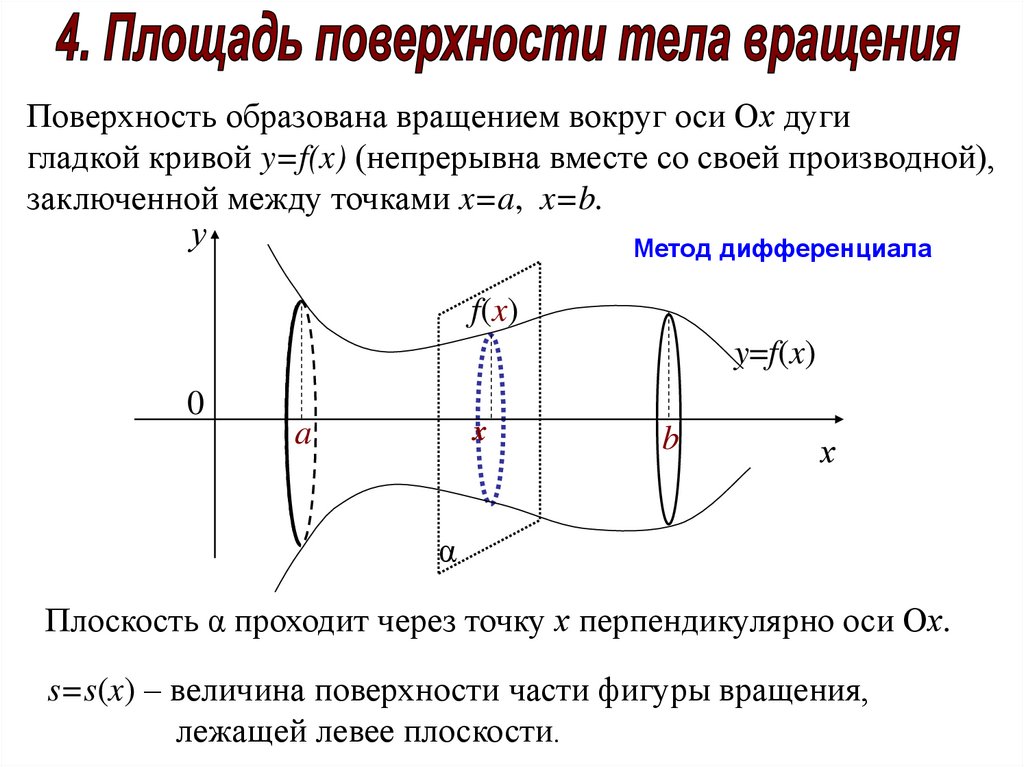
Поверхность образована вращением вокруг оси Ох дуги
гладкой кривой y=f(x) (непрерывна вместе со своей производной),
заключенной между точками x=a, x=b.
у
Метод дифференциала
f(x)
y=f(x)
0
a
x
b
х
α
Плоскость α проходит через точку х перпендикулярно оси Ох.
s=s(x) – величина поверхности части фигуры вращения,
лежащей левее плоскости.

7.

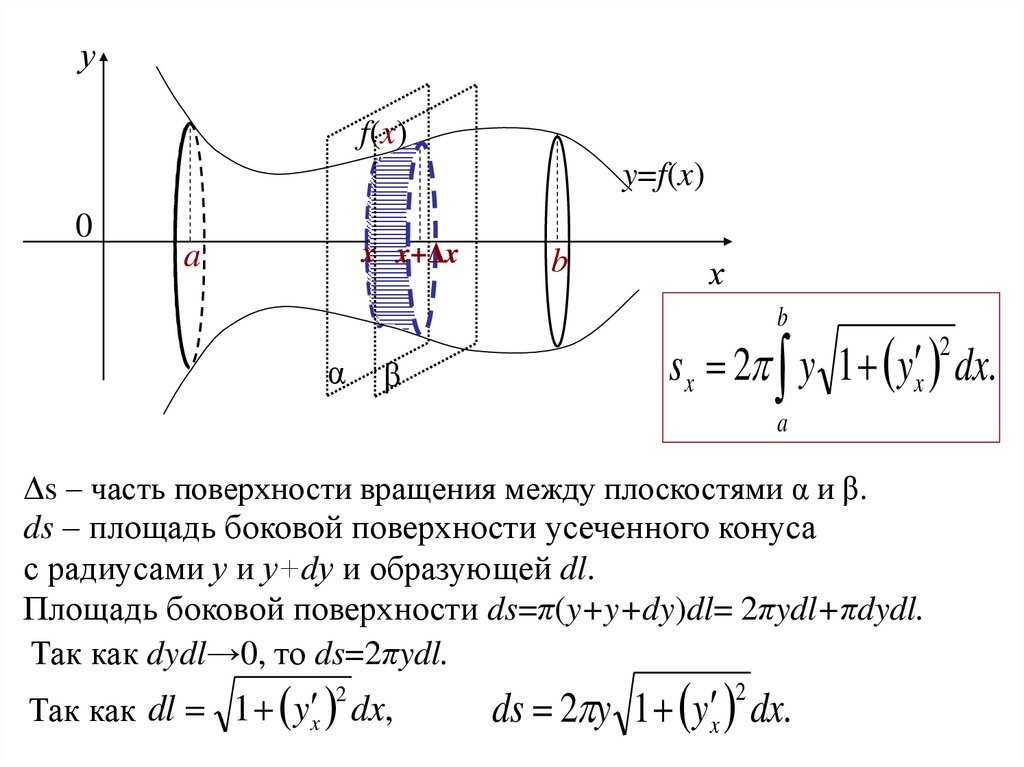
у
f(x)
y=f(x)
0
a
x x+Δx
b
х
b
α
β
sx 2 y 1 y x dx.
2
a
Δs – часть поверхности вращения между плоскостями α и β.
ds – площадь боковой поверхности усеченного конуса
с радиусами у и у+dу и образующей dl.
Площадь боковой поверхности ds=π(y+y+dy)dl= 2πydl+πdydl.
Так как dydl→0, то ds=2πydl.
Так как dl 1 y x dx,
2
ds 2 y 1 y x dx.
2

8.

Приложения
определенного интеграла
Физические приложения
определенного интеграла

9.

Пусть точка движется по некоторой кривой и
абсолютная величина её скорости v=v(t) есть функция
времени t , тогда путь, пройденный точкой за
промежуток времени t1 ≤ t ≤ t2, вычисляется по
формуле
t2
v=v(t)
s v(t )dt
t2
t1
t1

10.

Пусть переменная сила F=F(x) направлена
параллельно оси Ох. Под действием силы F точка
перемещается вдоль этой оси.
Тогда работа, произведенная силой при перемещении
точки на отрезке х1 ≤ х ≤ х2, вычисляется по формуле
x2
A F ( x)dx
x1
F=F(x)
х1
х2
х

11.

Закон Паскаля: сила давления жидкости (удельный
вес γ) на горизонтальную площадку S с глубиной
погружения h равна (вес соответствующего столба
жидкости) P hS
h
S
По этой формуле нельзя
искать давление жидкости на
вертикальную площадку.

12.

Пусть вертикальная площадка погружена в жидкость.
Она ограничена прямыми х=а, х=b и кривыми y=f(x), y=g(x).
Метод дифференциала
у
a
х
х+Δх
b
х
По закону Паскаля
dp x ( f ( x) g ( x))dx
h
S
Пусть х – произвольное значение
на отрезке [a;b].
p=p(x) – давление жидкости на
часть, соответствующую отрезку
[a;x].
Δр – давление на слой толщины Δх=dx.
dp – давление на прямоугольный
слой (горизонтальная площадка), все
точки которого находятся на одной
глубине х.
b
b
a
a
dp P x ( f ( x) g ( x))dx

13.

14.

b
Задача: найти определенный интеграл
a f ( x)dx
от непрерывной функции f(x).
Решение:
1) если можно найти
первообразную F(x)
функции f(x), то используем формулу
Ньютона – Лейбница;
2) если отыскание первообразных сложно
или она не выражается через элементарные функции (неберущиеся интегралы),
то используем формулы приближенных
вычислений определенных интегралов.
Абсолютная погрешность формул приближенных вычислений
b
~ ~ результат приближенного вычисления.
Rn f ( x ) dx I , I
a

15.

b
y
f ( x)dx ?S
к .т.
a
S
y = f (x)
f(ci)
0
a
х1
х2
хi-1 ci х
i
хn–1 b
х
1. Разобьем отрезок [a; b] на n равных частей длины
h
точками а=x0<х1<…<xn-1<xn=b (хi=a+ih, где i=0, 1, …,n).
x x
2. В середине ci i 1 i каждого отрезка [xi–1; xi] найдем f(ci).
2
3. Построим прямоугольники с основанием h и высотой f(ci).
4. Сумма площадей всех прямоугольников
n
f (c ) h
i 1
приближенно равна площади криволинейной трапеции.
i
b a
n

16.

у
y = f (x)
f(ci)
a
0
х1
хi-1 ci хi
х2
хn–1 b
х
b a n xi 1 xi
f (ci ) h
f
a f ( x)dx
n
2
i 1
i 1
Формула средних прямоугольников
(квадратурная формула прямоугольников).
b
n
Оценка абсолютной погрешности приближенного равенства:
3
b a M 2
, где М – наибольшее значение | f //(x)| на [a; b].
R
n
24n
2
2

17.

y
f(х1)
f(х2)
a
0
х1
f(хn–1) f(хn)
х
хn–1 b
х2
y = f (x)
Формула правых
прямоугольников
b a n
f xi
a f ( x)dx n
i 1
b
f(х0) f(х1)
y
f(х2)
f(хn–1)
0
a
х1
х2
b a n 1
f xi
a f ( x)dx n
i 0
b
хn–1
y = f (x)
b
х
Формула левых
прямоугольников

18.

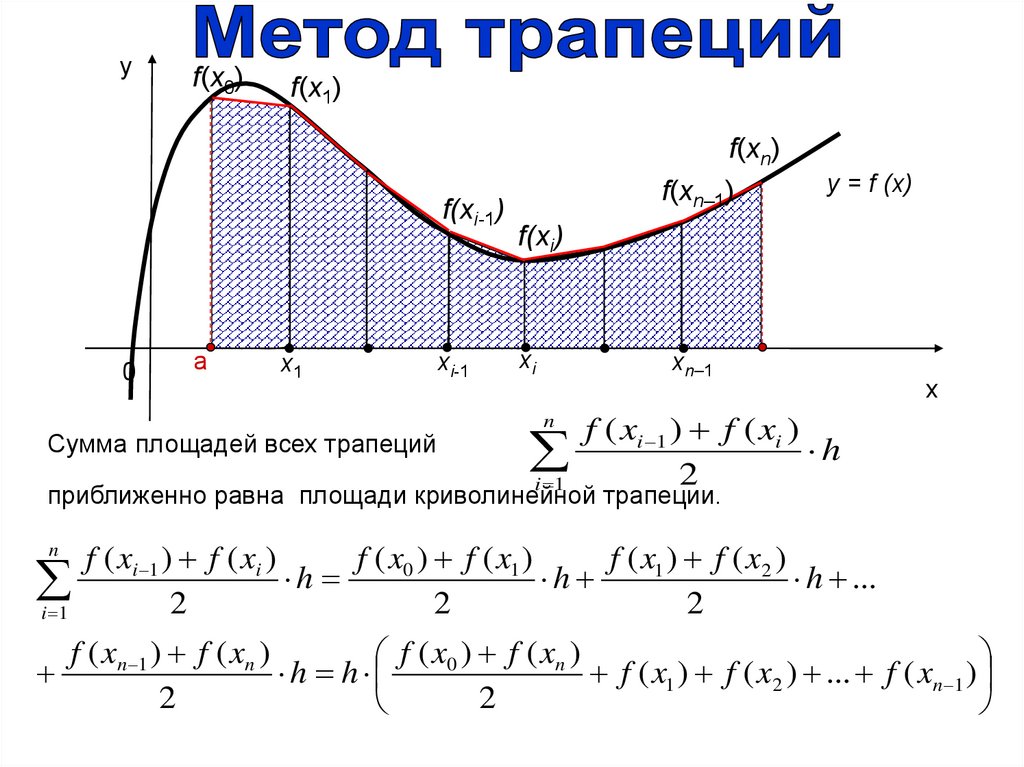
y
f(х0)
f(х1)
f(хi-1)
0
a
х1
Сумма площадей всех трапеций
хi-1
f(хn)
f(хn–1)
y = f (x)
f(хi)
хi
хn–1
b
х
f ( xi 1 ) f ( xi )
h
2
i 1
n
приближенно равна площади криволинейной трапеции.
f ( xi 1 ) f ( xi )
f ( x0 ) f ( x1 )
f ( x1 ) f ( x2 )
h
h
h ...
2
2
2
i 1
n
f ( xn 1 ) f ( xn )
f ( x0 ) f ( xn )
h h
f ( x1 ) f ( x2 ) ... f ( xn 1 )
2
2

19.

y
f(х0)
f(х1)
f(хi-1)
0
a
х1
хi-1
f(хn)
f(хn–1)
y = f (x)
f(хi)
хi
хn–1
b
х
Получим этот результат из формул прямоугольников (2 и 3).
b a n
f xi h f ( x1 ) f ( x2 ) ... f ( xn )
n
i 1
n 1
b a
f xi h f ( x0 ) f ( x1 ) ... f ( xn 1 )
n
i 0
f ( xi 1 ) f ( xi )
f ( x0 ) f ( xn )
h
f ( x1 ) f ( x2 ) ... f ( xn 1 )
2
2
i 1
n
h

20.

y
f(х0)
f(х1)
f(хi-1)
0
a
х1
хi-1
f(хn)
f(хn–1)
y = f (x)
f(хi)
хi
хn–1
b
х
b a f (a) f (b)
f ( x1 ) f ( x2 ) ... f ( xn 1 )
a f ( x)dx n
2
b
Формула трапеций (квадратурная формула трапеций).
Оценка абсолютной погрешности приближенного равенства:
3
b a M 2
, где М – наибольшее значение | f //(x)| на [a; b].
R
n
12n
2
2