Similar presentations:
Интегральное исчисление функции одной переменной
1.
Интегральное исчислениефункции одной переменной
2.
Неопределенныйинтеграл.
3.
Функция F(x) называется первообразнойфункцией для функции f(x), если F’(x) = f(x).
Совокупность всех первообразных функции
f(x) называется неопределенным
интегралом
f ( x)dx F ( x) C.
f(x) - подынтегральная функция
f(x)dx – подынтегральное выражение
х – переменная интегрирования
4.
Операция нахождения неопределенногоинтеграла от функции называется
интегрированием функции.
5.
Свойства неопределенного интеграла:1). f ( x) g ( x) dx f ( x)dx g ( x)dx.
2). k f ( x)dx k f ( x)dx.
3). dF ( x ) F ( x ) C
4).
f ( x)dx f ( x)
5). d f ( x )dx f ( x )dx
6.
Таблица основных неопределенных интегралов7.
Примеры1/ 3 1
x
33 4
xdx x dx
C
x C.
1/ 3 1
4
1)
2)
3 4 cos xdx 3x 4sin x C.
3
1/ 3
1
3
3)
dx arcsin x 3 ln x C
2
x
1 х
8.
11
3
3
4) 4 x
dx
dx 4 x dx
2
2
cos x
cos x
4x4
tgx C x 4 tgx C
4
5)
x 1
1
x dx 1 x dx x ln x C
9.
Основные методы интегрированияМетод подстановки
Метод подстановки заключается во введении
новой переменной интегрирования так,
чтобы заданный интеграл стал табличным.
Пусть требуется вычислить интеграл от
сложной функции,
f
t
dt
10.
Где t – промежуточный аргумент сложнойфункции, т.е.
t u( x ), где u( x ) функция, имеющия
непрерывную производную.
Тогда
dt u ( х )dх и получаем
f (u( x))u ( х)dx f (t )dt
11.
Следствие:1
Если f ( x)dx F ( x) C , то f (ax b)dx F (ax b) C.
a
Примеры
1.
2.
1
cos(3x 5)dx 3 sin( 3x 5) C
1
1
4 x 1dx 4 ln (4 x 1) C
12.
3.t sin x
1
cos x
cos x
cos x dx cos2 x dx 1 sin 2 x dx dt d sin x
dt cos xdx
dt
1 t 1
1 sin x 1
ln
C ln
C.
2
1 t
2 t 1
2 sin x 1
13.
Метод интегрирования по частямПусть u(x) и v(x) – функции имеющие
непрерывные производные.
Формула интегрирования по частям имеет
вид:
14.
При интегрировании по частямнеобходимо
1. подынтегральное выражение
представляется в виде двух сомножителей
u(x) и dv,
2. находят v (интегрируя dv) и du
(дифференцируя и),
3. Используют формулу интегрирования по
частям.
Иногда эту формулу приходится использовать
несколько раз.
15.
Пример1.
xe
dx
x
u x
dv e dx
du dx
v e
x
x
x e e dx x e e c
x
x
x
x
16.
2.u ln x
dv xdx
x ln xdx
1
x
du dx v
x
2
2
x 1
2
dx
x
ln x 2 x
2
2
2
2
2
x
1
x
x
ln x xdx
ln x
c
2
2
2
4
17.
3.u x dv cos xdx
x cos xdx du dx v sin x
x sin x sin xdx x sin x cos x c
18.
Метод неопределенных коэффициентовМетод неопределенных коэффициентов
применяют при интегрировании
рациональных дробей.
Рациональной дробью называется дробь
вида
,
где P(x) и Q(x) являются многочленами.
19.
Рациональная дробь называется правильной,если степень числителя P(x) ниже степени
знаменателя Q(x); в противном случае
дробь называют неправильной.
Любая правильная рациональная
дробь может быть единственным образом
представлена в виде суммы простых
рациональных дробей.
20.
Простые рациональные дроби:1)
;
2)
, где m - целое число, больше единицы;
3)
, где квадратный трехчлен не имеет
действительных корней;
4)
, где n - целое число, больше единицы,
и квадратный трехчлен
не имеет
действительных корней.
21.
ПримерВыполнить деление многочлена на многочлен
x5 6 x3 2 x 2 4
x2 x 1




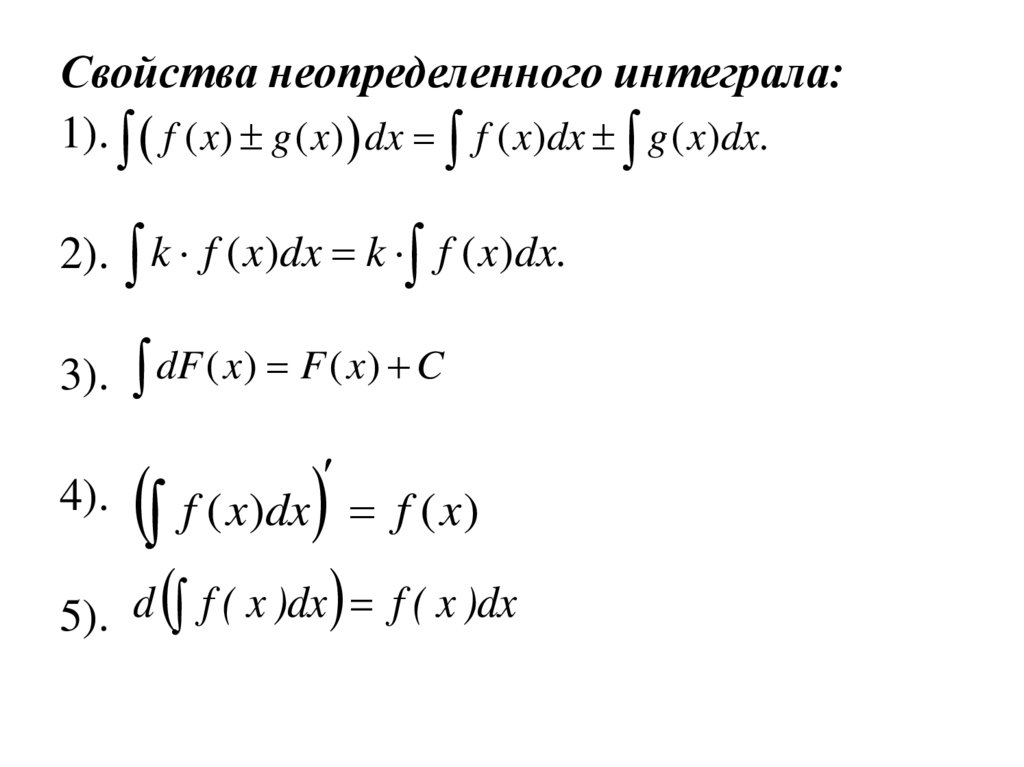


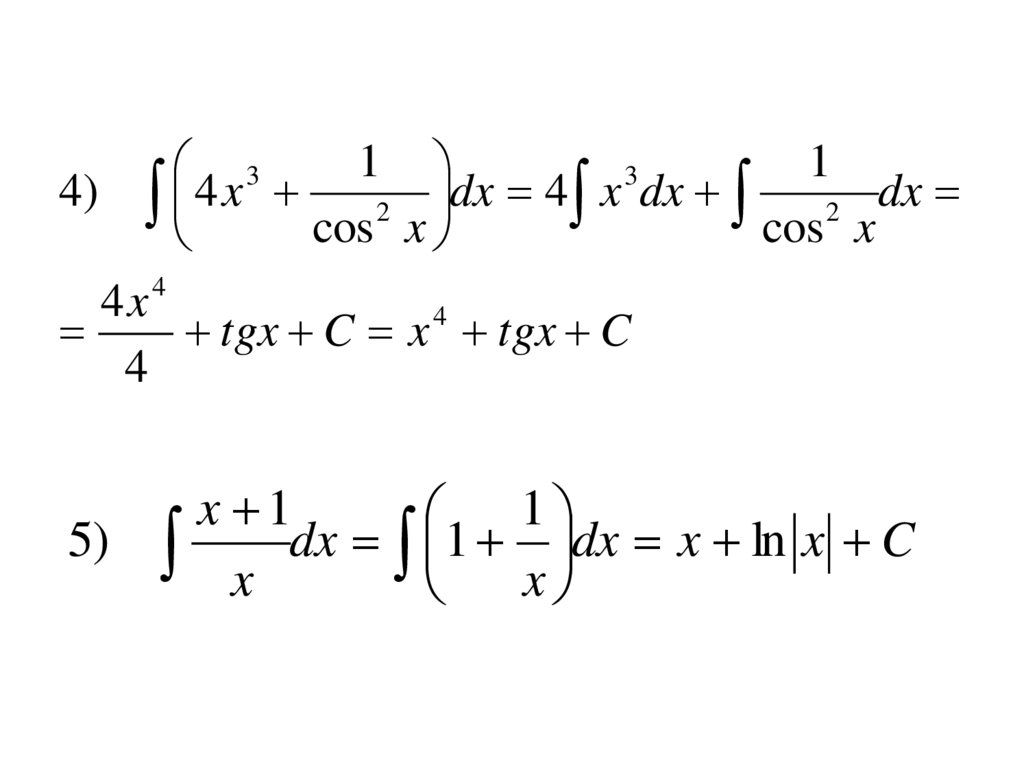



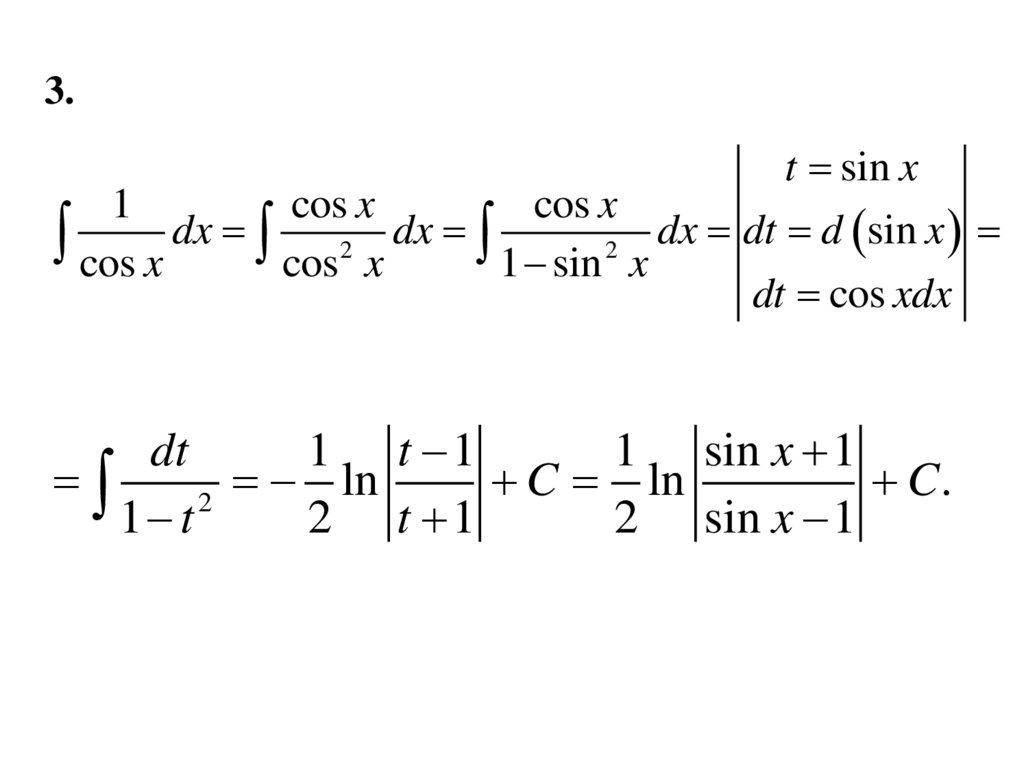


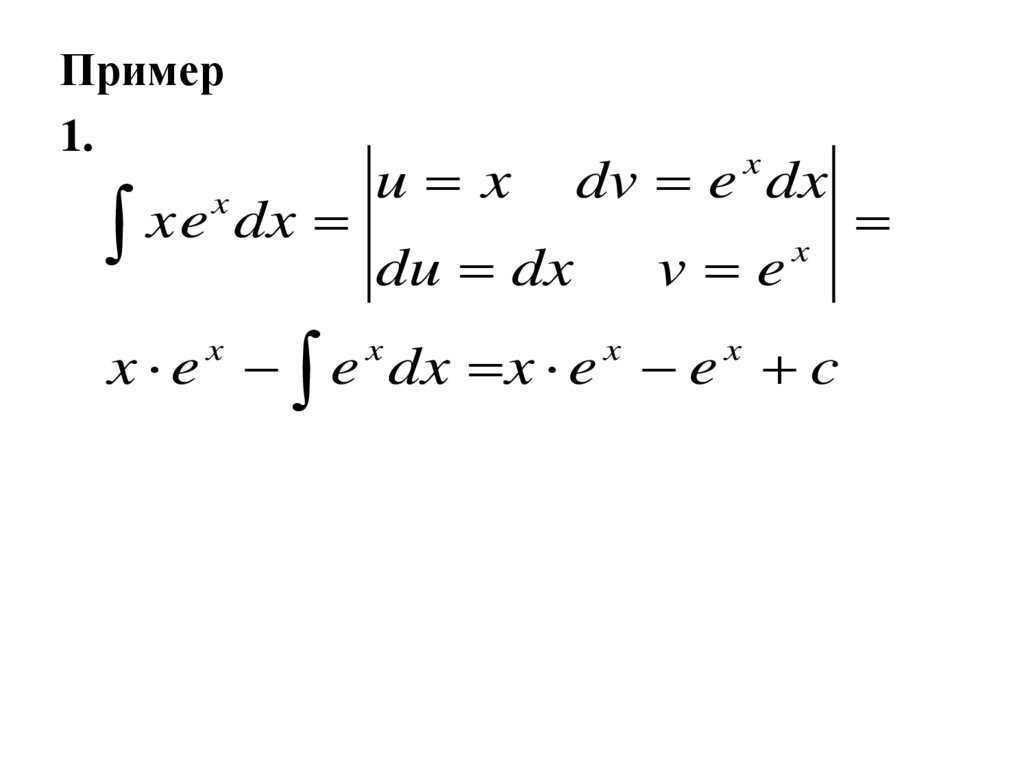
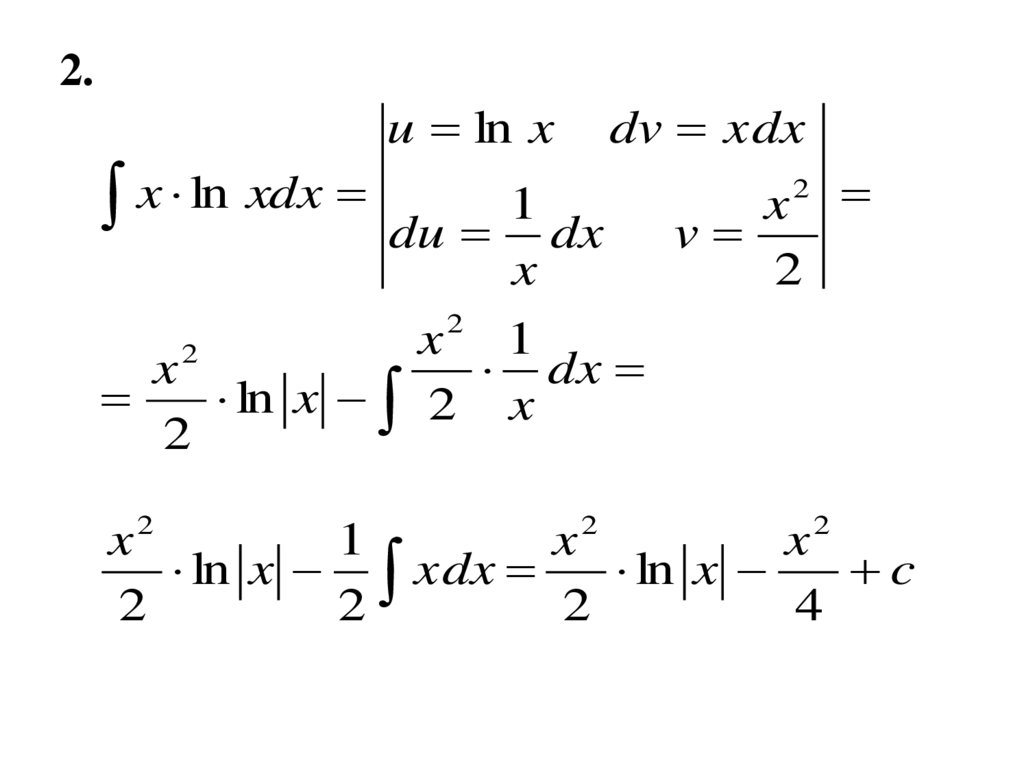
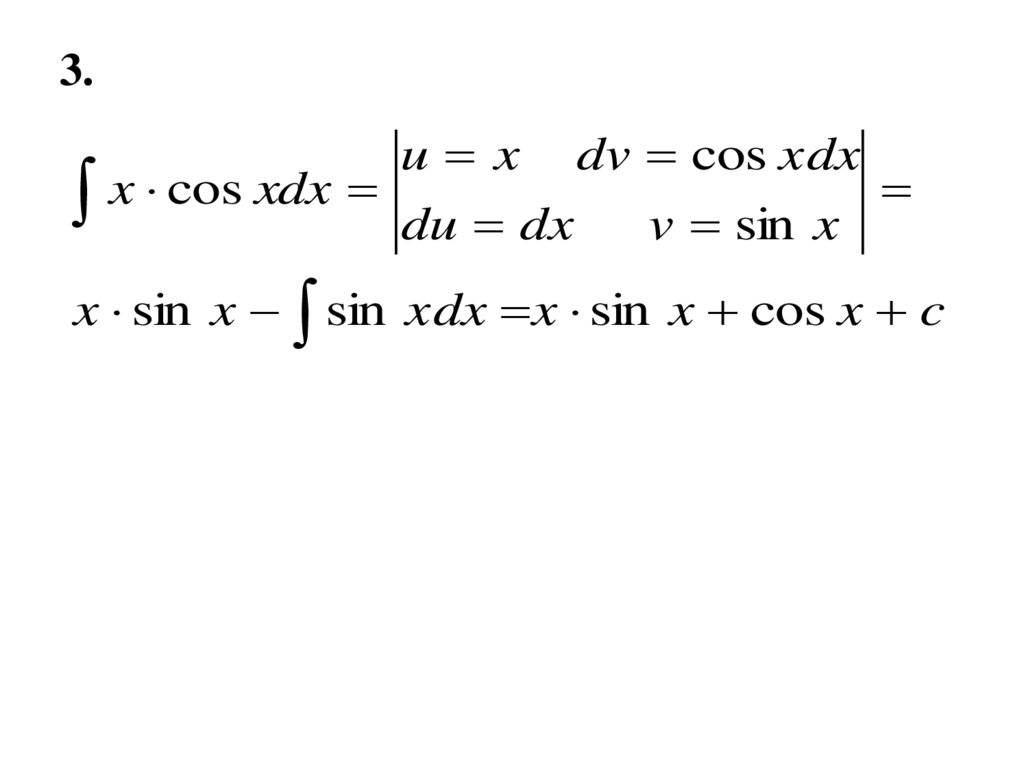






 mathematics
mathematics








