Similar presentations:
Интегральное исчисление функции одной переменной. Первообразная функции. Неопределенный интеграл. Метод замены переменной
1.
Тема. Интегральное исчисление функцииодной переменной. Первообразная функции.
Неопределенный интеграл. Метод замены
переменной. Метод интегрирования по частям.
Основные вопросы/план темы
1.Первообразная функции.
2. Неопределенный интеграл.
3.Основные свойства неопределенного интеграла.
4.Таблица основных интегралов.
5.Метод замены переменной.
6. Метод интегрирования по частям.
2.
Функция F(x) называется первообразнойфункции f(x) на промежутке Х, если в
каждой точке х этого промежутка
F ( x) f ( x)
3.
4x
F ( x)
4
Например, функция
является первообразной для функции
f ( x) x
поскольку
3
x
3
x
4
Для заданной функции f(x) ее первообразная
определена не однозначно.
4
Например, функции
4
x
1;
4
4
4
x
x
2 ; ...
const
4
4
тоже являются
функции х3.
первообразными
для
4.
В общем случае, если F(x) –первообразная для функции f(x), то
функция вида F(x)+С тоже является
первообразной для f(x), поскольку
( F ( x) C ) F ( x) f ( x)
5.
Из геометрического смысла производнойвытекает, что
F (x)
есть угловой коэффициент касательной к
кривой y=F(x) в точке х.
Найти первообразную для функции f(x),
значит найти такую кривую y=F(x),
что угловой коэффициент
касательной к ней в произвольной
точке х равен значению f(x).
6.
Если F1(x) и F2(x) - первообразныефункции f(x) на некотором
промежутке Х, то найдется
такое число С, что будет
справедливо равенство:
F2 ( x) F1 ( x) C
7.
Из этой теоремы следует, что если F(x) –первообразная для функции f(x), то
выражение
F ( x) C
задает все возможные первообразные для
функции f(x).
8.
Совокупность всех первообразных дляфункции f(x) на промежутке Х
называется неопределенным
интегралом от функции f(x).
f ( x)dx F ( x) C
Функция f(x) называется
подынтегральной функцией.
Выражение f(x)dx называется
подынтегральным выражением.
9.
4x
x dx 4 C
3
Интегрирование
является
операцией,
обратной дифференцированию.
Для проверки правильности результата
интегрирования надо продифференцировать
результат и получить подынтегральную
функцию.
10.
1Производная от неопределенного интеграла
равна подынтегральной функции.
f ( x)dx f ( x)
11.
f ( x)dx F ( x) CF ( x) f ( x)
12.
2Дифференциал от неопределенного интеграла
равен подынтегральному выражению.
d
f ( x)dx f ( x)dx
13.
df ( x)dx f ( x)dx dx
f ( x)dx
14.
3Неопределенный интеграл от дифференциала
некоторой функции равен этой функции с
точностью до постоянного слагаемого.
dF
(
x
)
F
(
x
)
C
15.
Представим функцию F(x) как первообразнуюнекоторой функции f(x).
Тогда:
f ( x)dx F ( x) C
Отсюда
:
f ( x)dx dF ( x)
Следовательно:
dF( x) f ( x)dx F ( x) C
16.
4Постоянный множитель можно выносить за
знак неопределенного интеграла.
k f ( x)dx k f ( x)dx
17.
Этосвойство
вытекает
производной функции F(x):
k F ( x)
из
свойства
k F ( x) k f ( x)
18.
5Интеграл от алгебраической суммы
(разности) двух функций равен сумме
(разности) интегралов от этих функций:
( f ( x) g ( x))dx f ( x)dx g ( x)dx
19.
ПустьF(x) и G(x) – первообразные для
функций f(x) и g(x). Тогда
F ( x) G ( x)
F ( x) G ( x) f ( x) g ( x)
20.
1n 1
x
x dx n 1 C
n
n 1
21.
21
dx
ln
x
C
x
22.
3x
a
a
dx
C
ln a
x
a 0, a 1
23.
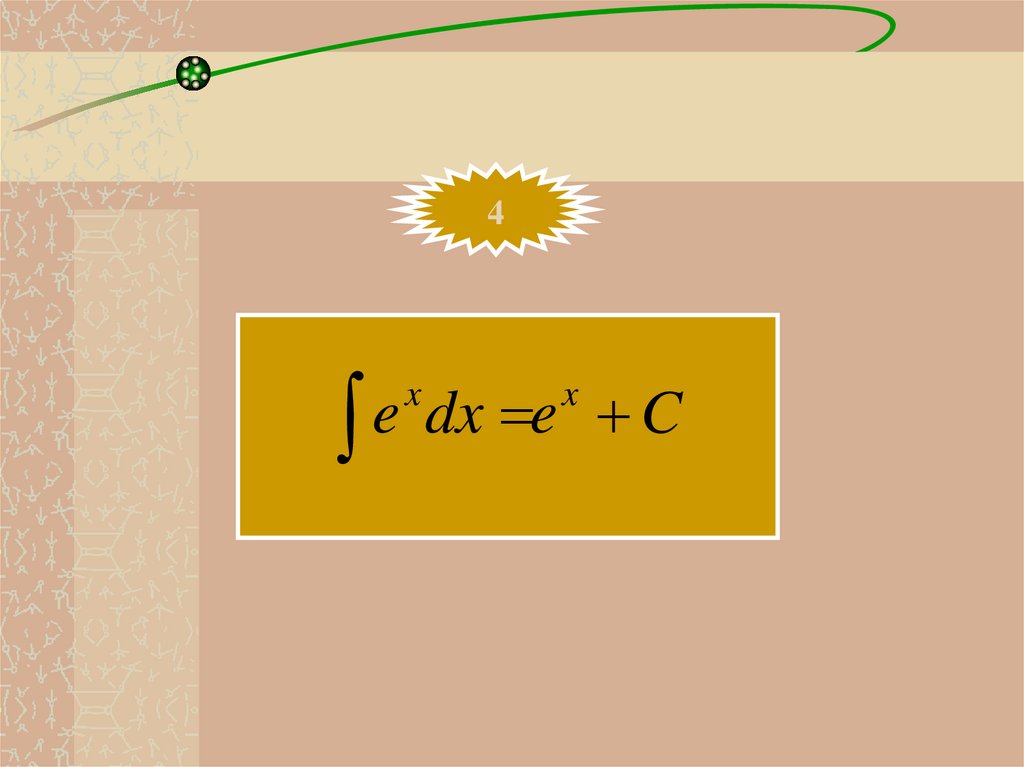
4e dx e
x
x
C
24.
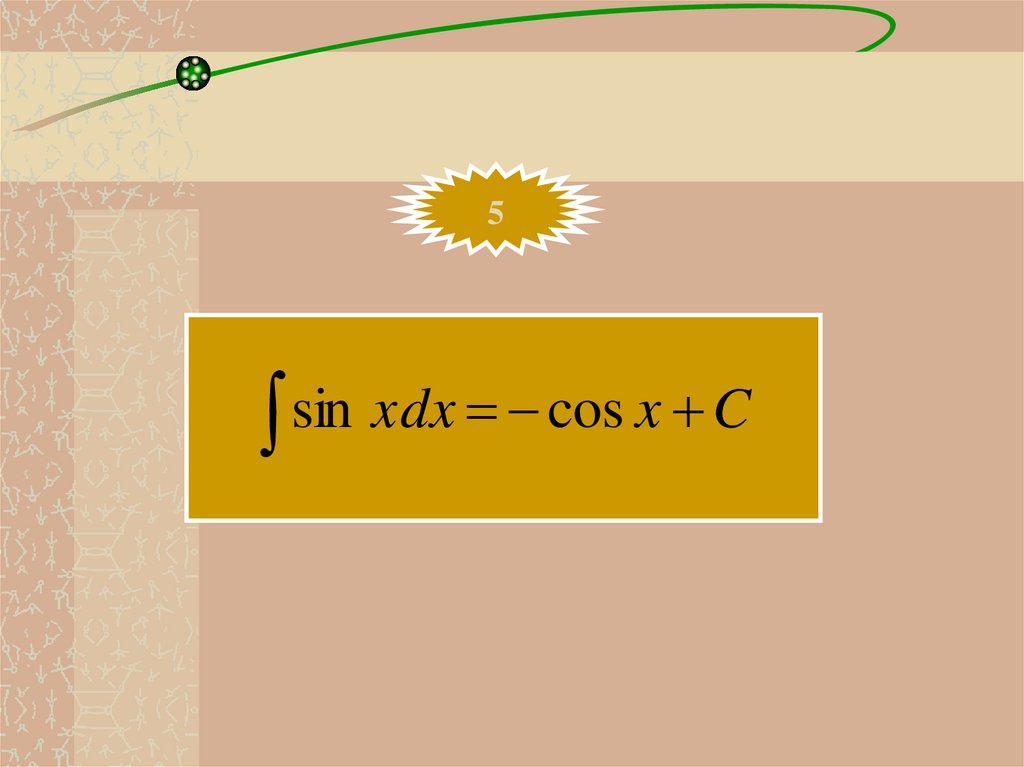
5sin xdx cos x C
25.
6cos xdx sin x C
26.
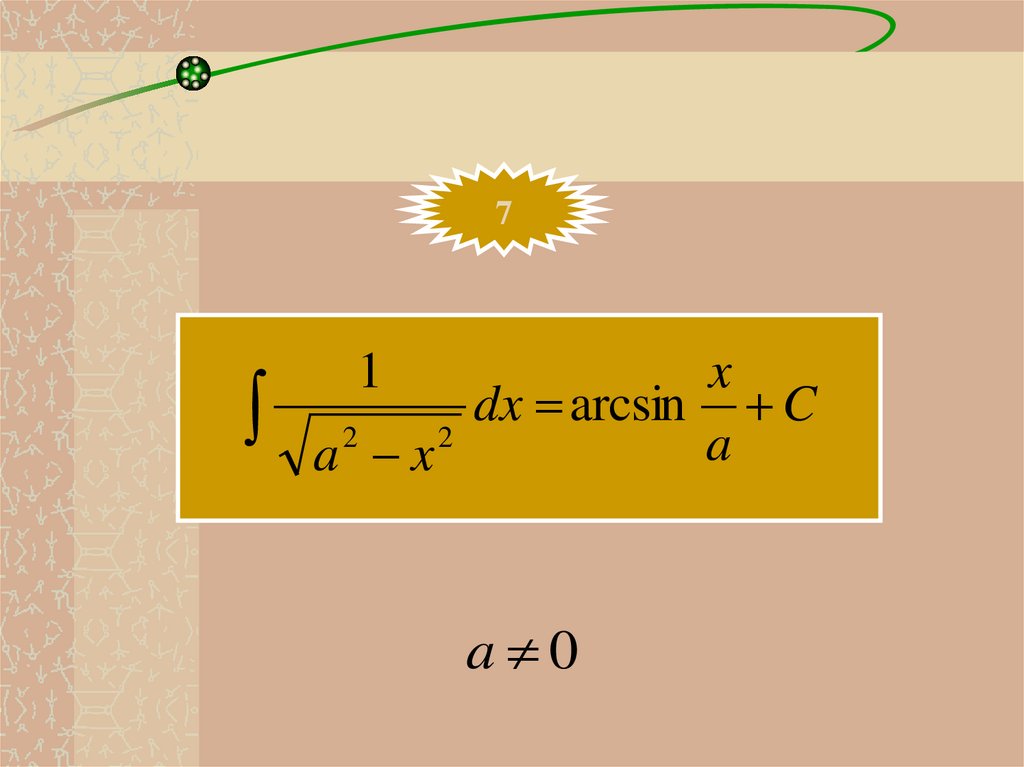
71
x
dx arcsin C
2
2
a
a x
a 0
27.
81
1
x
dx
arctg
C
2
2
a x
a
a
a 0
28.
91
1
x a
x 2 a 2 dx 2a ln x a C
a 0
29.
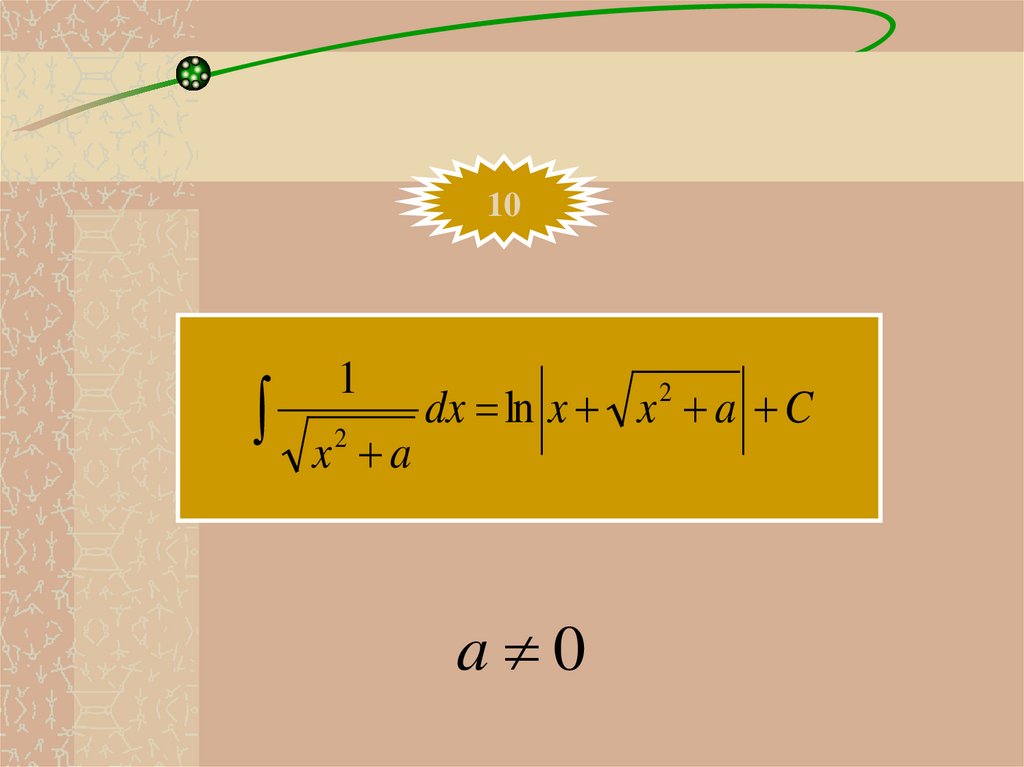
101
x a
2
dx ln x x a C
2
a 0
30.
111
cos 2 x dx tgx C
31.
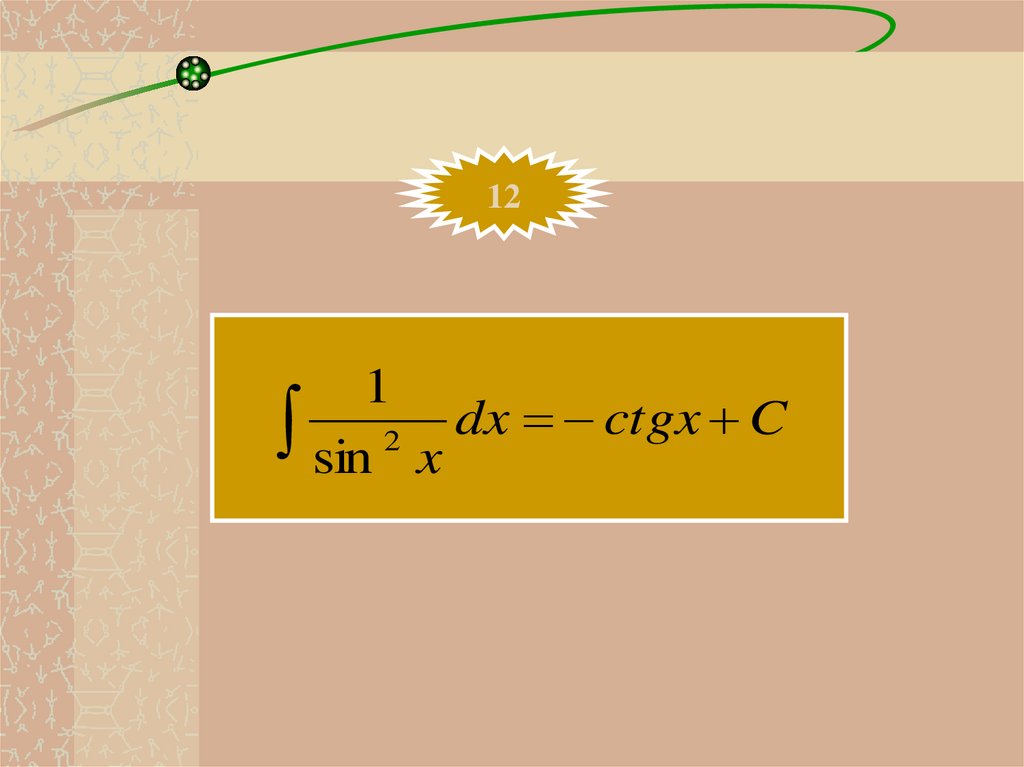
121
sin 2 x dx ctgx C
32.
Вычисление интегралов с помощью основныхсвойств неопределенного интеграла и
таблицы
интегралов
называется
непосредственным
или
элементарным
интегрированием.
33.
Вычислить интегралы:1
2
(6
3
x
2sin x)dx
34.
(2sin x 6 3x2
)dx
6dx 3x dx 2sin xdx
2
6 dx 3 x dx 2 sin xdx
2
6 x x 2cos x C
3
35.
23x x x 2
dx
2
x
4
3
36.
3x 4 x 3 x 2dx
2
x
1
1
2
3 x x 2 2 dx
x
x
1
1
3 x dx xdx dx 2 2 dx
x
x
2
2
x
2
3
x
ln x C
2
x
37.
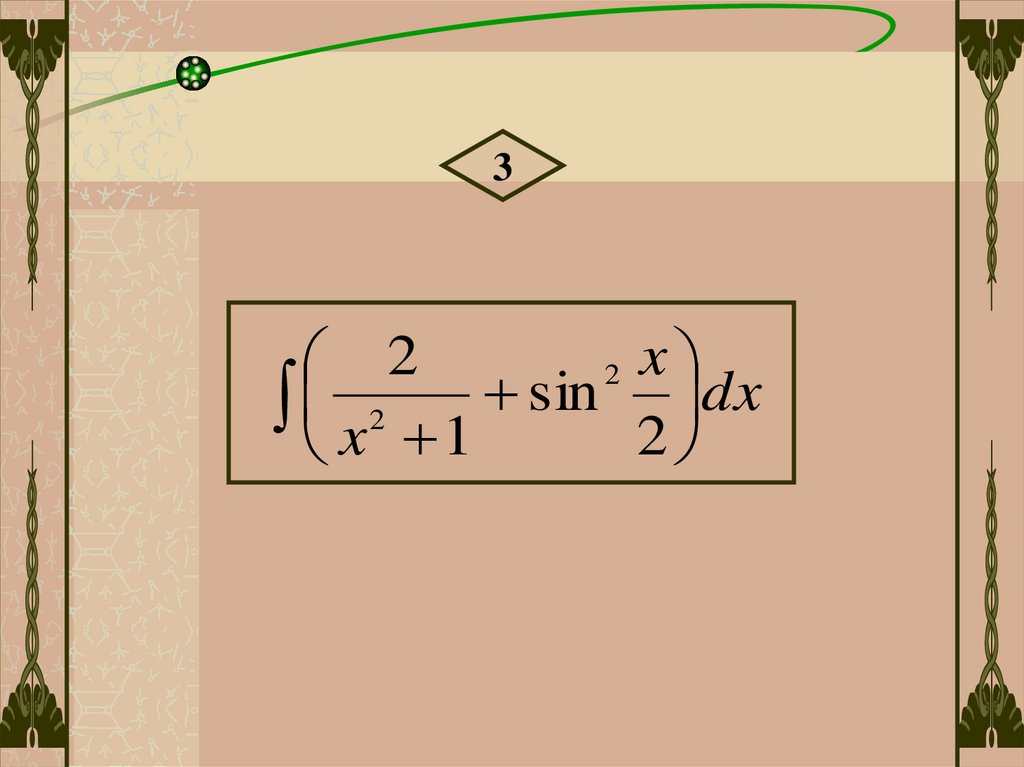
32
2 x
x 2 1 sin 2 dx
38.
22 x
x 2 1 sin 2 dx
1
2 x
2 2
dx sin
dx
x 1
2
1
2arctgx (1 cos x)dx
2
1
1
2arctgx x sin x C
2
2
39.
Метод заменыформулой:
переменной
описывается
f ( x)dx f ( (t )) (t )dt
1
40.
Где х=φ(t) – функция, дифференцируемая нарассматриваемом промежутке.
Покажем справедливость этой формулы.
Найдем производную по t от левой и правой
части выражения (1):
f ( x)dx f ( x)dx
t
x
xt f ( x) (t )
f ( (t)) (t)dt
t
f ( (t )) (t ) f ( x) (t )
41.
Получилиодинаковый
результат,
следовательно по следствию из теоремы
Лагранжа
левая
и
правая
части
выражения (1) отличаются на некоторую
постоянную.
Т.к.
сами
неопределенные
интегралы
определены с точностью до произвольного
постоянного слагаемого, то эту постоянную
можно опустить.
Т.об,
f ( x)dx f ( (t )) (t )dt
42.
Полученнаяформула
показывает,
что
переходя к новой переменной, достаточно
выполнить
замену
переменной
в
подынтегральном выражении.
Удачная замена переменной позволяет
упростить исходный интеграл и в
некоторых
случаях
свести
его
к
табличному.
43.
Вычислить интегралы:1
x( x 1)
12
dx
44.
x 1 tx( x 1)
12
dx x t 1
dx dt
(t 1) t 12dt t 12dt t 13dt
t
t
( x 1)
( x 1)
C
C
13 14
13
14
13
14
13
14
45.
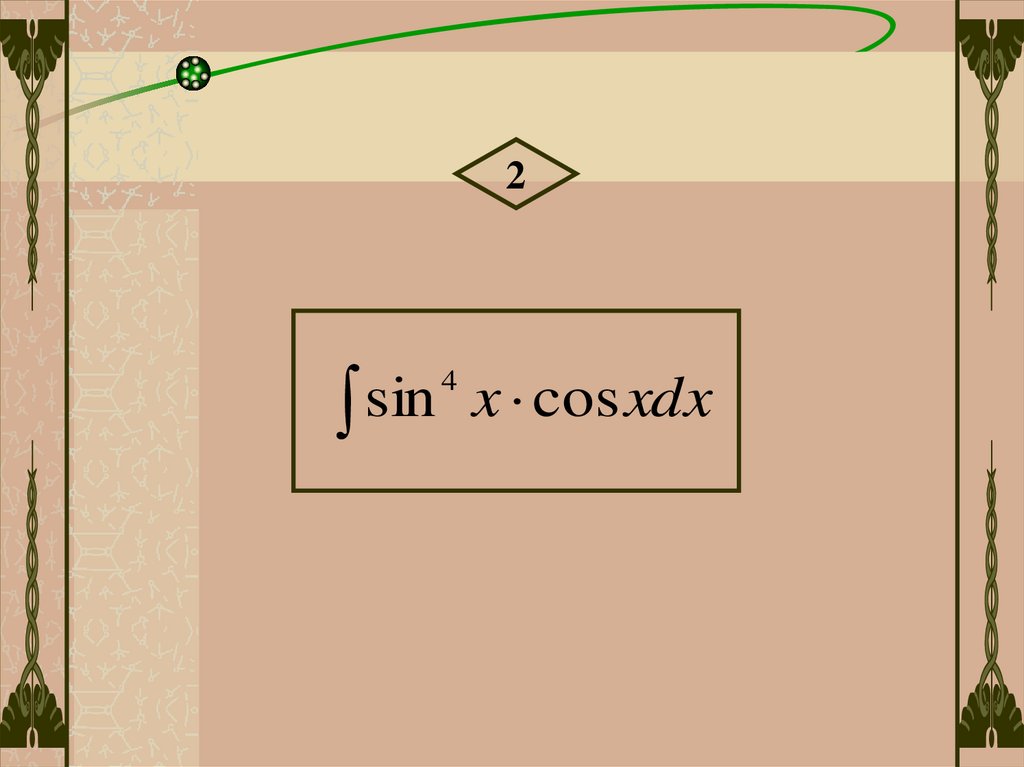
2sin
4
x cos xdx
46.
sin4
x cos xdx
sin x t
dt cos xdx
dt
1 5
1
t dt t C sin 5 x C
5
5
4
47.
Пусть F(x) – некотораяпервообразная для функции f(x).
Тогда
1
f (kx b)dx F (kx b) C
k
48.
Вычислить интегралы:1
3
3 xdx
49.
3k 1
4
3
3
3 xdx
(3 x) C
b 3
4
50.
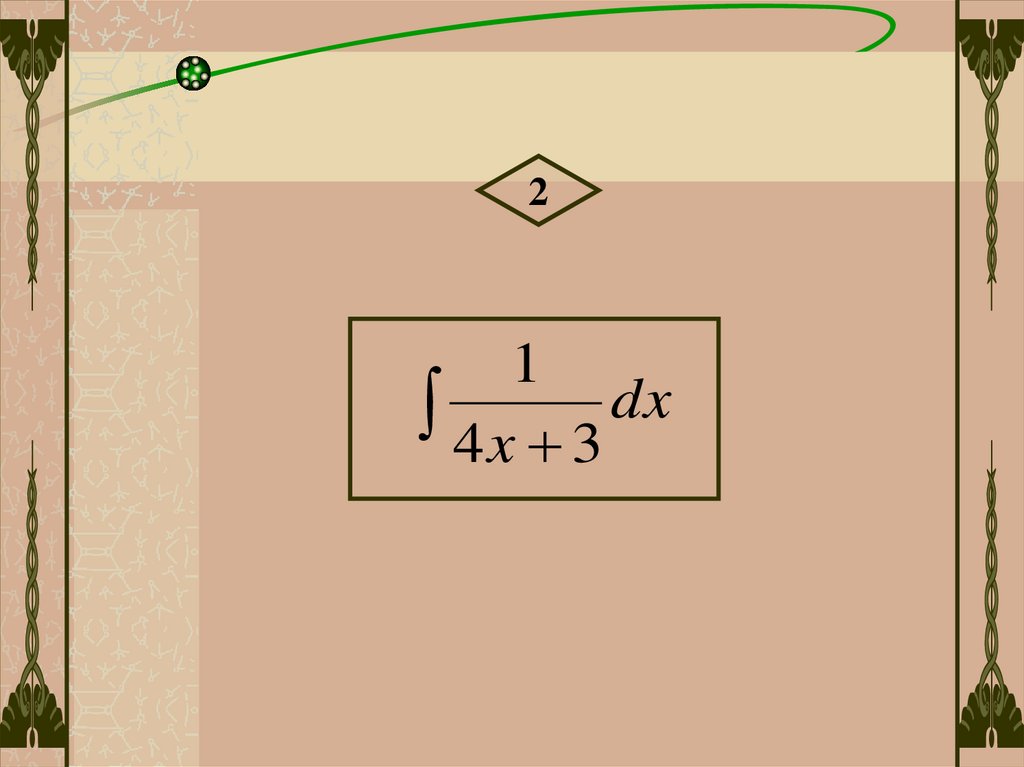
21
4 x 3 dx
51.
k 4 11
4 x 3 dx b 3 4 ln 4 x 3 C
52.
Пусть функции u(x) и v(x)определены и дифференцируемы на
промежутке Х и функция
u ( x) v( x)
имеет первообразную на этом
промежутке.
53.
Тогда функцияv ( x) u ( x)
тоже имеет первообразную на
этом промежутке и справедлива
формула
u( x) v ( x)dx u( x) v( x) v( x) u ( x)dx
54.
Найдем производную произведения данныхфункций:
u( x) v( x)
u ( x) v( x) u ( x) v ( x)
Отсюда выражаем второе слагаемое в правой
части выражения:
u ( x) v ( x) u ( x) v( x) u ( x) v( x)
55.
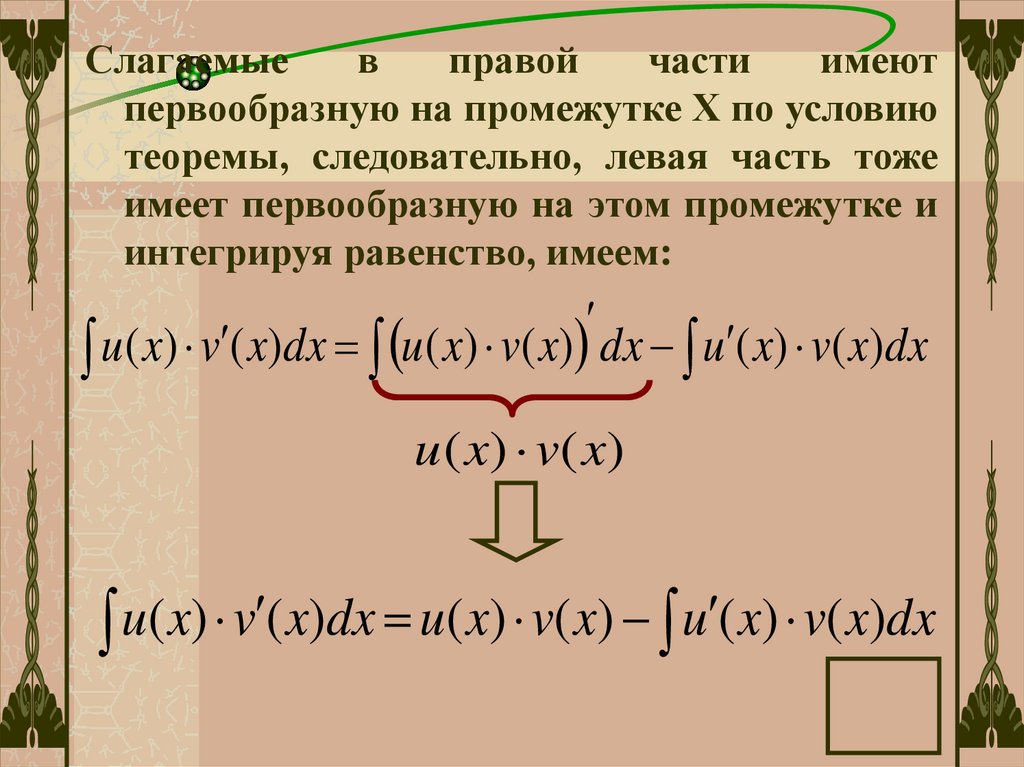
Слагаемыев
правой
части
имеют
первообразную на промежутке Х по условию
теоремы, следовательно, левая часть тоже
имеет первообразную на этом промежутке и
интегрируя равенство, имеем:
u( x) v ( x)dx u( x) v( x) dx u ( x) v( x)dx
u ( x) v( x)
u
(
x
)
v
(
x
)
dx
u
(
x
)
v
(
x
)
u
( x) v( x)dx
56.
Посколькуu ( x)dx du
v ( x)dx dv
То последнее равенство часто записывают в
виде:
u
dv
u
v
v
du
57.
Вычислить интегралы:1
x e
x
dx
u
dv
u
v
v
du
58.
u xx e dx du dx
x
dv e dx
x
v e
x
x e e dx x e e C
x
x
x
x
59.
2ln xdx
60.
u ln x1
ln
xdx
du dx
x
dv dx
v x
x
x ln x dx x ln x x C
x
61.
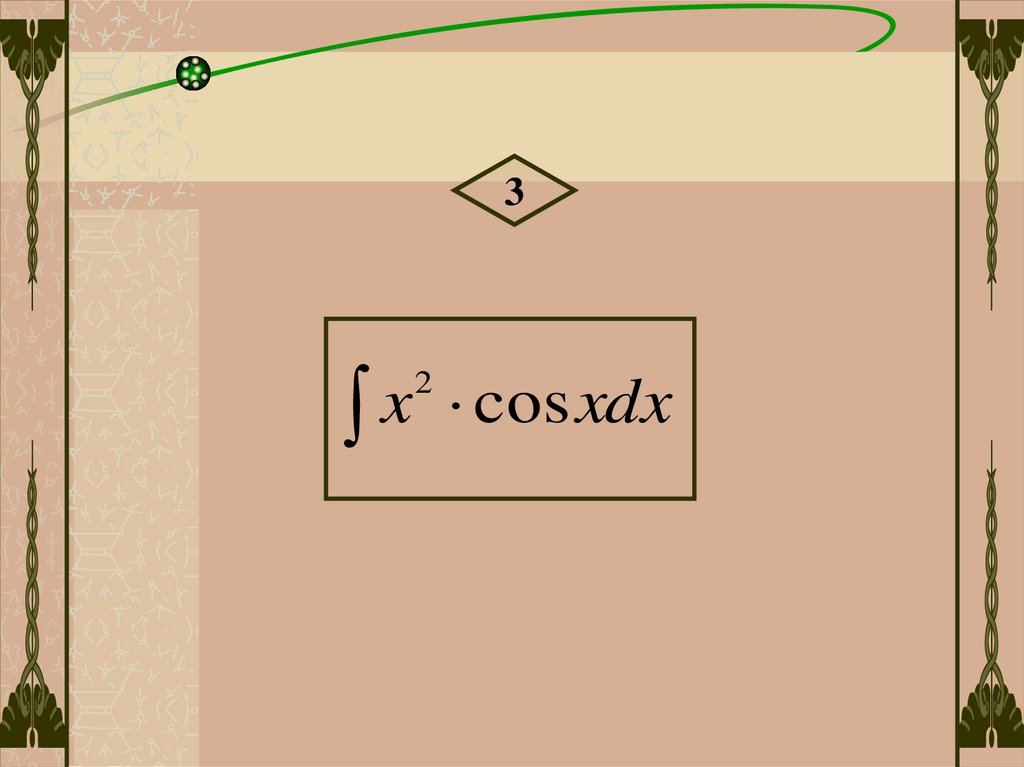
3x
2
cos xdx
62.
x2
cos xdx
u x2
dv cos xdx
du 2 xdx
v sin x
x cos x 2 x sin xdx
2
u x
dv sin xdx
du dx
v cos x
x cos x 2 x cos x 2 cos xdx
2
x cos x 2 x cos x 2 sin x C
2
63.
Можнопоказать,
что
формула
интегрирования по частям применима для
следующих типов интегралов:
x
x
n
n
e dx
ax
cosmxdx
x
n
x
sin mxdx
k
ln xdx
n
64.
xk
arcsin xdx
x
k
arctgxdx
x
k
arccosxdx
x
k
arcctgxdx
Где a, m, k – действительные числа, n – целое
положительное число.












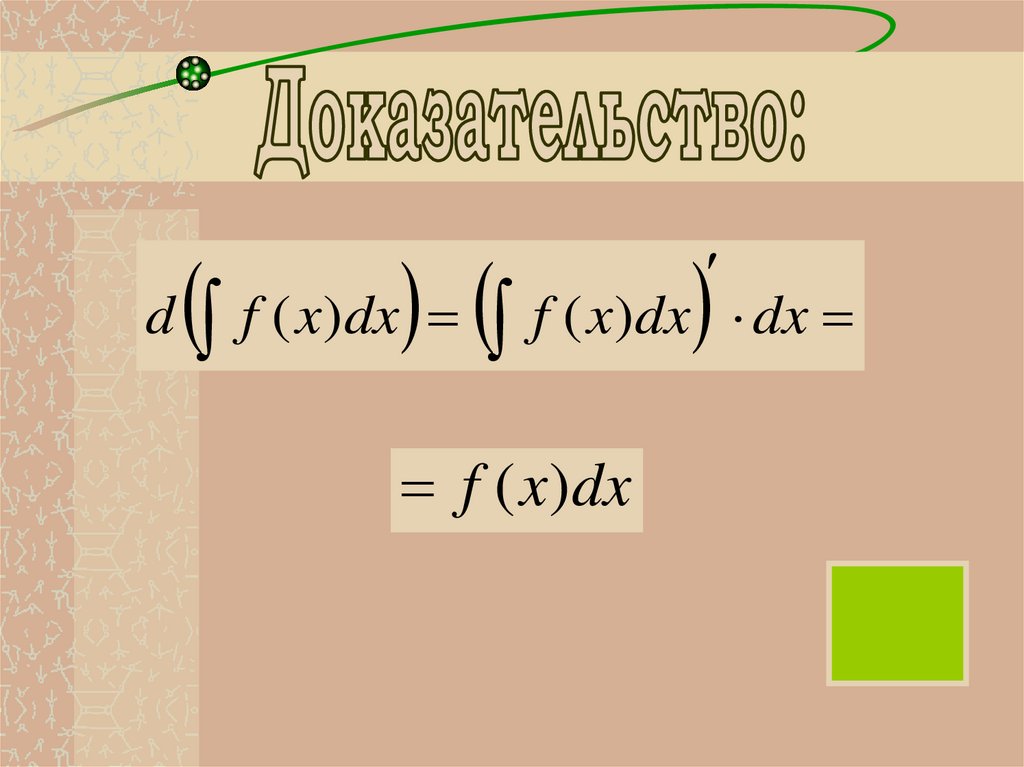

























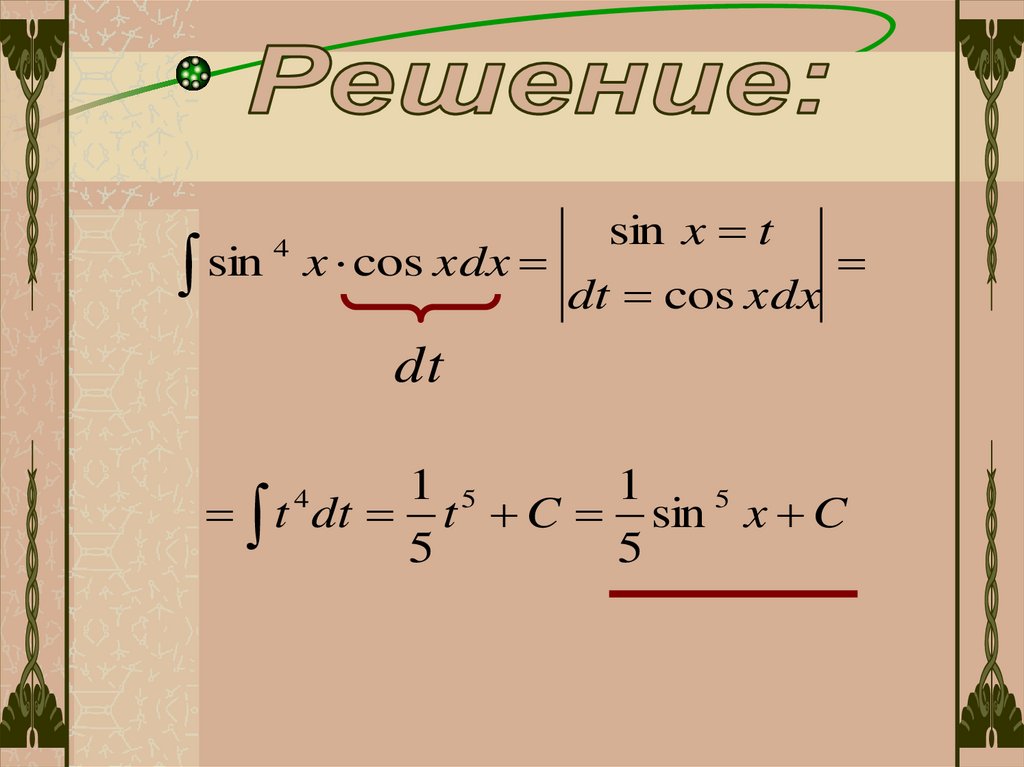


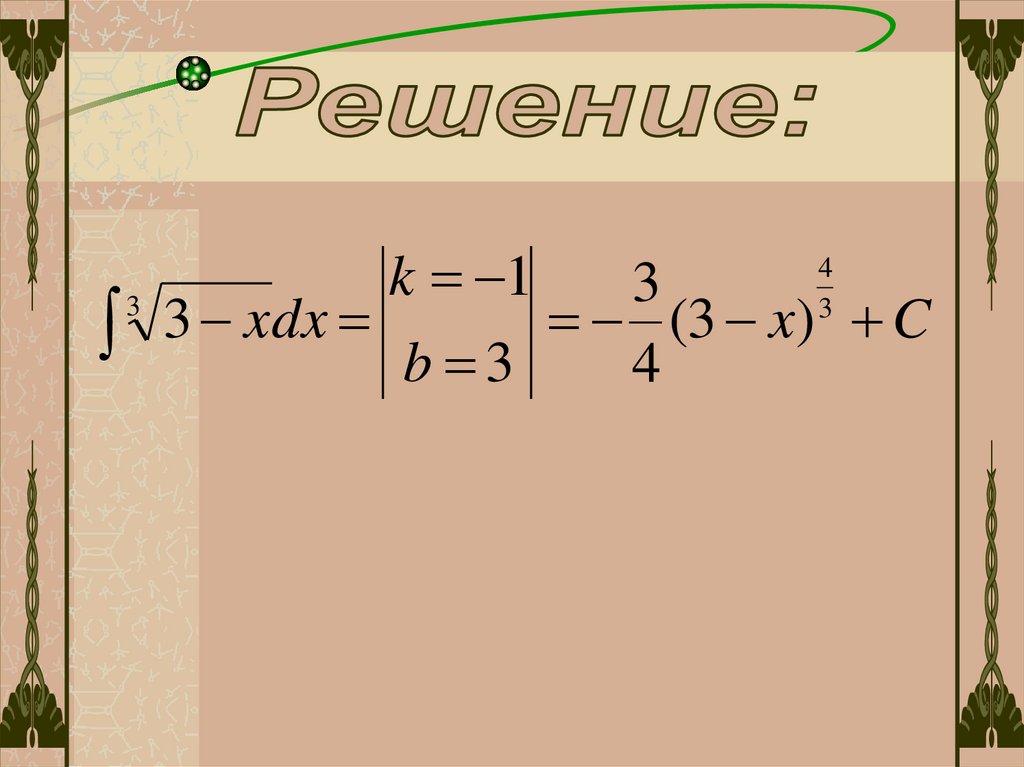






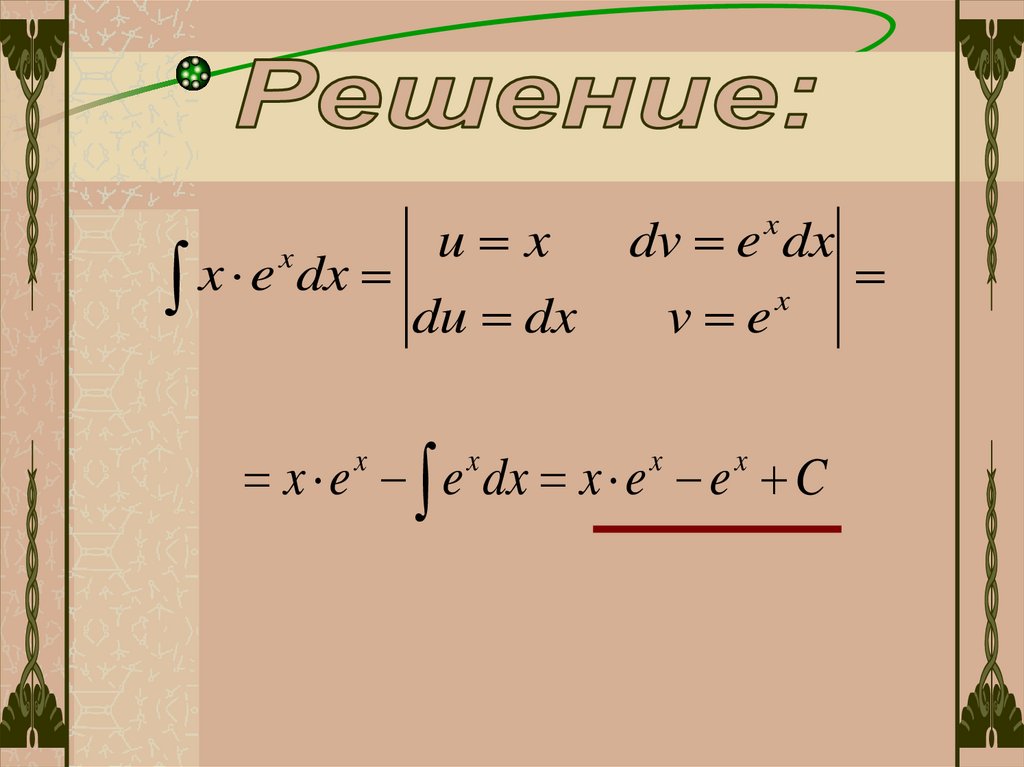





 mathematics
mathematics








