Первообразная. Неопределенный интеграл

1.

ЕН.01 МАТЕМАТИКА

2.

Основные вопросы:
Определение первообразной. Основное
свойство первообразной.
Понятие неопределенного интеграла.
Основные формулы интегрирования.
Непосредственное интегрирование (метод
разложения).
Этапы интегрирования функций методом
подстановки (замены переменной).
Метод по частям.
Интегрирование некоторых
тригонометрических функций

3.

Определение первообразной. Основное
свойство первообразной.
Первообразной функцией по отношению
к данной функции у = f(x) называется такая
функция F(x), производная от которой равна
данной функции, т.е.
Для данной функции у = f(x) первообразных функций
бесчисленное множество, т.к. любая из функций F(x)
+ С, также является первообразной для у = f(x).

4.

Понятие неопределенного интеграла.
Основные формулы интегрирования
Совокупность всех первообразных
F(x) + С для данной функции у = f(x)
называется ее неопределенным интегралом
обозначается символом:
где f(x)dx - называется подынтегральным выражением,
функция f(x) - подынтегральной функцией.

5.

Геометрически, неопределенный интеграл
представляет собой семейство
интегральных кривых на плоскости,
полученных путем параллельного переноса
графика функции у = F(x) вдоль оси ординат

6.

5
x
x dx 5 C
4
поскольку функция
x 5 - первообразная для функции х4.
5
Процесс нахождения неопределенного интеграла
функции называется интегрированием этой функции.

7.

Свойства неопределенного интеграла:
1. Производная неопределенного
интеграла равна подынтегральной
функции:
( f ( x)dx) f ( x)
Это свойство считается очень важным, его используют
для проверки правильности вычисления интеграла.

8.

Свойства неопределенного интеграла:
2. Дифференциал от неопределенного
интеграла равен подынтегральному
выражению:

9.

Свойства неопределенного интеграла:
3. Неопределенный интеграл от
дифференциала функции равен этой
функции плюс произвольная
постоянная:

10.

Свойства неопределенного интеграла:
4.Постоянный множитель можно
выносить за знак неопределенного
интеграла:
kf
(
x
)
dx
k
f
(
x
)
dx

11.

Свойства неопределенного интеграла:
5.Неопределенный интеграл от суммы 2-х
функций равен сумме неопределенных
интегралов от этих функций:

12.

Функция
Степенная
Интеграл

13.

Функция
Показательная
Интеграл

14.

Функция
Тригонометрические
Интеграл

15.

Функция
Обратные
тригонометрические
Интеграл

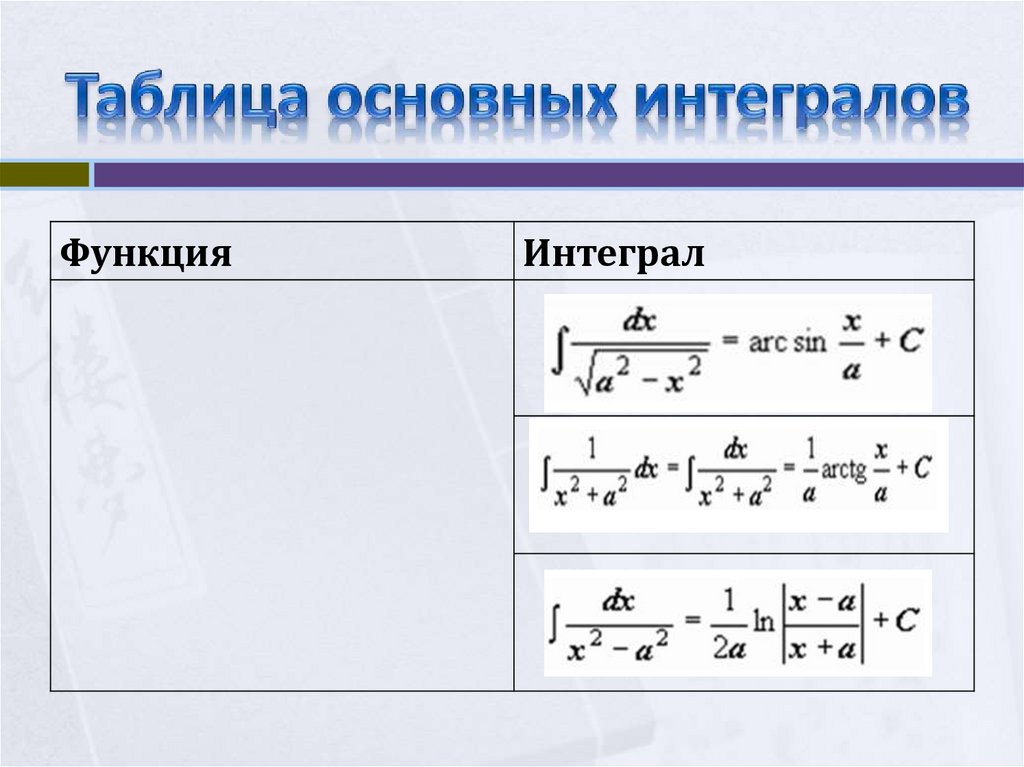
16.

Функция
Интеграл

17.

18.

19.

Непосредственное
интегрирование
– это метод, основанный на
применении тождественных
преобразований подынтегральной
функции, а также основных
свойств неопределенного интеграла
и табличных
интегралов.

20.

Наиболее часто используются
следующие преобразования
подынтегральной функции:
Деление числителя на знаменатель
почленно;
Применение формул сокращенного
умножения;
Применение тригонометрических
тождеств.

21.

Проверка:
Проверка:

22.

Используя свойство неопределенного интеграла, вынесем
за знак интеграла постоянный множитель.
Затем, выполняя элементарные математические
преобразования, приведем подынтегральную функцию к
степенному виду:
1
2
3
2
5
2
2x
4 5
2 x xdx 2 x x dx 2 x dx 2 5 5 x C

23.

3 x 2x
dx
x
3
Решение:
2
3 3 х2 2х
3 3 x2 2x
dx
dx
х
x
х
х
1
1
12
6
2
3 x x 2 x dx
1
2
7
6
3
2
2 3x
6 x
2 2x
1
7
3
66 7 4 3
6 x
x
x C
7
3

24.

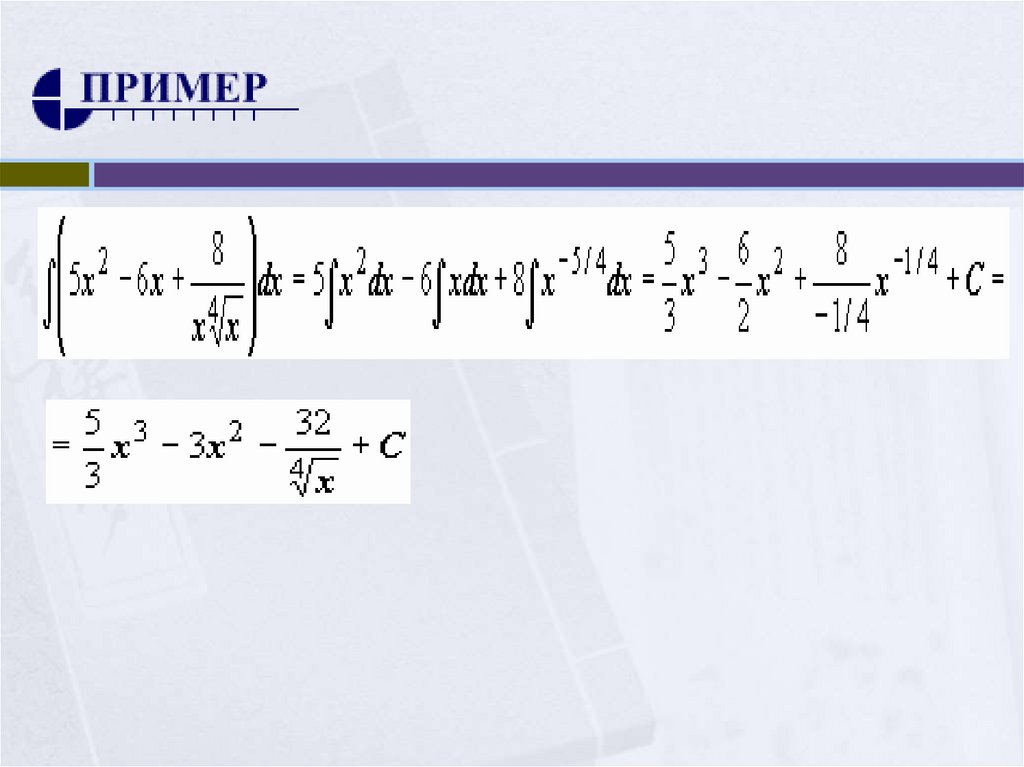
25.

3 2 x dx
2
Решение:
3 2 x dx 9 12
2
3
2
х 4 х dx
2 12 x
4x
3
2
9x
C 9x 8 x 2x C
3
2
2

26.

ctg
2
xdx
Решение:
cos x
1 sin x
ctg
xdx
dx
dx
sin 2 x sin 2 x
1
2 1 dx ctgx x C
sin x
2
2
2

27.

28.

29.

Чаще всего этот метод
используется, если в
подынтегральном выражении
содержится сложная функция,
тогда ее промежуточный аргумент
и надо обозначить как новую
переменную.

30.

Далее необходимо выполнить следующие действия:
• Найти дифференциал новой переменной
;
• Записать прежний интеграл, используя только
переменную t, если подстановка сделана правильно, то
полученный интеграл
должен быть
табличным;
• используя таблицу интегралов, записать решение для
подынтегральной функции
;
• Осуществить обратную подстановку, заменив
переменную
t.

31.

Найти
5
(
5
x
3
)
dx
Решение: введем подстановку u = 5x + 3
дифференциал этого выражения:
d (5x + 3) = du
5dx = du, откуда
dx = 1/5 du
Подставив вместо 5х +3 и dx их значения в
данный интеграл, получим:
6
1 5
1 u
1 6
(5x 3) dx 5 u du 5 6 c 30 u c
5

32.

Заменив u его выражением через x, имеем:
1
6
(5x 3) dx 30 (5x 3) c
5
Проверка:
1
6
6
d (5 x 3) c (5 x 3) 5 5 dx (5 x 3) 5 dx
30
30
Интеграл найден правильно.

33.

3
x
x
1
dx
Решение:
t3 x 1 x t3 1
t 3 x 1
d ( x 1) d (t 3 )
dx 3t dt
2
Заменяя переменную в данном интеграле, имеем:
7
4
t
t
3
2
6
3
3
x
x
1
dx
(
t
1
)
t
3
t
dt
3
(
t
t
)dt 3( c
7 4)
Подставляя вместо t его выражение через x, найдем:
(3 x 1)7 (3 x 1) 4
( x 1) 2 3 x 1 ( x 1) 4 x 1
) c
x x 1 dx 3( 7 4 ) c 3(
7
4
3
( x 1) (4 x 3) 3 x 1 c
28
3

34.

du
1
1
sin(5x 3) dx sin u 5 5 cos u c 5 cos(5x 3) c
5x 3 u
d (5 x 3) du
5dx du
du
dx
5

35.

Сделаем замену переменной t = sin x, тогда
dt = (sin x)′dx = cos x dx.
Исходный интеграл имеет вид:
sin x cos xdx
2
t sin x
dt cos xdx
t 2 dt
Таким образом, мы получили неопределенный интеграл
табличного вида: степенная функция.
Используя правило нахождения неопределенного интеграла от
степенной функции, найдем:

36.

3
t
2
t
dt 3 C
Сделав обратную замену, получим окончательный
ответ:
1 3
sin x cos xdx 3 sin x C
2
1 3
Ответ: sin x C
3

37.

x
Решение:
4
4
2 x dx
2
2 x2 t
2
4
2
x
t
2
4
x
2
x
dx
2
4
2 x dx t dt
2 xdx 4t dt; xdx 2t dt
3
3
5
2
t
2t 3 tdt 2t 4 dt
C 0,4t 5 C
5
0,4 2 х
4
2 5
С

38.

x
e
dx
x2
Решение:
х2 t
x2
2
x e dx x dx t dt
dt
2 xdx dt; xdx
2
1 t
1 t
1 t
x2
e dt e dt e C 0,5e C
2
2
2

39.

40.

– это метод, заключающийся в
использовании формулы:

41.

• Данный метод интегрирования основан на
тождестве:
d uv udv vdu udv d uv vdu
где u = f(x) и v = φ(x) - две функции, имеющие на
данном промежутке производные.
Взяв интеграл от обеих частей данного
тождества, будем иметь:
u
dv
d
uv
v
du
u
dv
uv
v
du

42.

x
2
ln xdx
Решение:
u ln x du ln x dx
dx
x
ln
x
dx
dv
x
dx
du
x
1 3
2
v x dx x
3
2
2

43.

3
3
x
x dx
x ln xdx uv vdu ln x 3 3 x
3
1 3
1 x
1 3
1 3
x ln x x ln x x C
3
3 3 3
9
2
1 3
1 3
Ответ: x ln x x C
3
9

44.

x
cos
6
x
dx
Решение:
u x du dx
x cos 6 xdx dv cos 6 xdx
1
v cos 6 xdx sin 6 x
6
1
1
x cos 6 xdx uv vdu 6 x sin 6 x 6 sin 6 xdx
1
1
x sin 6 x cos 6 x C
6
36
Ответ:
1
1
x sin 6 x cos 6 x C
6
36

45.

46.

Интегралы от произведений синусов и
косинусов с разными аргументами, линейно
зависящими от , упрощаются, если
применить тригонометрические формулы
преобразования произведения в сумму:

47.

Вычислим интеграл
Преобразуем произведение
сумму:
тогда
в

48.

Колесов В.В. Математика для медицинских
колледжей: учебное пособие/В.В.Колесов, М.Н.
Романов. – Ростов н/Д: Феникс, 2015 – 316 с.: ил.(среднее медицинское образование). Гл.10, §10.1 10.2.
Используя материал презентации Занятие
5_НеопределенИнтеграл, выполните из РАБОЧЕЙ
ТЕТРАДИ, ТЕМА 2.2, Занятие 5. Понятие
первообразной функции и неопределенного
интеграла