Similar presentations:
Интегралы функции одной переменной
1.
ТЕМА: Интегралы функции однойпеременной
ВОПРОС 1. Неопределенный интеграл
ВОПРОС 2. Определенный интеграл
ВОПРОС 3. Приложения определенных
интегралов
2.
1.Определение. Функция F (x) называется
первообразной функции f (x) на множестве
X , если для любого x X выполняется
равенство F ( x) f ( x) .
Определение.
Множество
всех
F
(
x
)
C
первообразных
функций
для
f (x )
называется
неопределенным
интегралом от функции f (x) и обозначается
символом
Т.е.
f ( x)dx .
f ( x)dx F ( x) C
3.
Таблица интегралов1
u
u du
C,
1.
1
2.
1 .
du
ln u C
,
u
u
a
a du
C
3.
,
ln a
u
e
du
e
C
4.
,
u
u
sin
udu
cos
u
C
5.
,
cos
udu
sin
u
C
6.
du
tg
u
C
2
7. cos u
,
,
4.
duu
arcsin
C
2 2
a
1.
,
a u
du
u a
2
ln u u a C
2
2
2
,
du
1
u
arctg
C
2 2 a
,
a
u a
du
1
u a
ln
C
2 2 2a u a
,
u a
5.
6.
Метод замены переменнойМетод замены переменной состоит в том,
что в интеграл f ( x)dx , нахождение которого
затруднительно, вводят новую переменную
t,
связанную
соотношением
t
где
функция,
с
переменной
x
x t ,
–
непрерывная монотонная
имеющая
непрерывную
t
производную
интервале изменения t .
на
некотором
7.
Таким образом,f ( x)dx f (t ) (t )dt
После того, как интеграл найден,
возвращаются к первоначальной переменной
1
t
(
x
)
с помощью подстановки
.
Пример:
ln x
dx
t
ln x
dx
t
ln
x
,
dt
tdt
C
C
x
x
2
2
2
2
8.
Метод интегрирования по частямИнтегрирования по частям основано на
применении формулы
udv
u
v
vdu
Случаи применения формулы по частям.
kx
kx
P
(
x
)
e
dx
Pn ( x) a
dx
n
I.
;
;
dv
dv
u
u
Pn ( x) cos
kxdx
;
u
dv
P
(
x
)
sin
kxdx
n
.
u
dv
9.
P(
x
)
arcsin
mxdx
P
(
x
)
arccos
mxdx
II. n
; n
;
P
(
x
)
arctg
mxdx
n
;
P
(
x
)
arcctg
mxdx
n
;
P
(
x
)
ln
mxdx
n
.
10.
dvP
(
x
)
dx
n
За
,
u arcsin mx ,
u arccos mx ,
u arctgmx ,
u arcctgmx ,
u ln mx .
11.
e sin bxdx ,ax
III.
e
cos
bxdx
.
ax
Применяется двукратное интегрирование
по частям.
Пример:
du
dx
u x
x 3x 1 3x
x 3x 1 3x
3x
1
x
e
dx
e
e
dx
e
e
C
3
x
3x
v
e
e dx dv
3
3
3
9
3
.
12.
Интегрирование рациональных функцийНайдем
интегралы
рациональных дробей:
простейших
A
d ( x a)
dx A
A ln x a C .
x a
x a
от
A
dx
A
(
x
a
)
k
x a
.
Ax B dx
x px q
2
k
x a
d ( x a) A
1 k
1 k
I
,
C, k Z , k 1
13.
2p
q 0
где 4
, т.е. квадратный трехчлен
x px q 0
корней.
2
не имеет действительных
A
2 B Ap
2x p
2
I ln x px q
arctg
C
2
2
.
2
4q p
4q p
14.
Пример:в числителе выделим
x 1
dx
2
x 3x 5
производную знаменателя
2
x 3x 5 2 x 3
1
x 1 (2 x 3) 1
2
1 (2 x 3)dx 1
2
2 x 3x 5 2
1
(2 x 3) 1 dx
2
2
x 3x 5
3
d x
2
dx
1 d ( x 3x 5) 1
2
2
2
x 2 3x 5 2
x 2 3x 5
3
11
x
2
4
3
x 2
1
1 2
2
2
ln x 3 x 5
arctg
C
2
2 11
11
1
1
(2 x 3)
2
ln x 3 x 5
arctg
C.
2
11
11
15.
Интегрирование выражений, содержащихтригонометрические функции
Интегралы
1.
sin
x
cos
xdx
,
где
m
,
n
Z
вида:
.
m
а)
Если
n
m 0
нечетное,
то
подстановка
приводит
интегралу от рациональной функции.
к
Если
t cos x
n 0
и
и нечетное, то к тому же
приводит подстановка
t sin x .
16.
mn
б) Если оба показателя
и
положительные и четные, то применяются
формулы:
1
cos x 1 cos 2 x ,
2
1
2
sin x 1 cos 2 x ,
2
sin 2 x
sin x cos x
.
2
2
17.
mn
в) Если оба
показателя
и
отрицательные и сумма их четная, то
t tg x (t ctg x)
подстановка
приводит
к интегралу от рациональной функции.
2
t
2
sin x
2
При этом
,
1 t
1
cos x
2 ,
1 t
2
dx
dt
.
1 t
2
18.
1. Интегралы вида:n
tg xdx
x
tg
t
сводится к
путем подстановки
интегралу от рациональной функции, при
dt
x arctg t , dx
2
1 t
этом
2.
Формулы:
sin x cos xdx :
.
Интегралы вида:
1
sin cos sin sin ,
2
19.
20.
Примеры:1.
sin x 1 cos x
2
sin xdx sin x sin xdx t cos x
2
3
dt sin xdx
2
1 t dt
3
2
3
cos x
t
C .
dt t dt t C cos x
3
3
2
2.
1
1
1
sin 6 x cos xdx 2 sin 5x sin 7 x dx 2 sin 5xdx 2 sin 7 xdx
1
1
cos 5x cos 7 x C
.
14
10
21.
3.t tg x
5
dt
tg
xdx
dx
2
1 t
4
2
t
t
3
dt
t
t
dt
2
2
1 t
t 1
5
t
t
1
1 4
1 2
1
2
2
ln t 1 C tg x tg x ln tg x 1 C
4 2 2
4
2
2
.
22.
2. Определенный интегралf
(
x
)
0
a;
b
Если
на
, то определенный
b
f ( x ) dx
интеграл
представляет
собой
площадь
a
криволинейной
трапеции
–
фигуры,
ограниченной y=f(x)
линиями
y f ( xy ), x a, x b, y 0
0
a
Рис. 1
b
x
(рис. 1).
23.
Формула Ньютона-Лейбница:b
f x dx F x F b F a ,
b
a
a
где
F x – первообразная для f x .
Интегрирование по частям:
b
b
a
b
udv u v vdu
a
a
,
u
u
x
,
v
v
x
где
a;
b
дифференцируемые функции на
.
–
24.
Замена переменной:b
x t
f x dx dx t dt f t t dt ,
a
где
x t –
функция
непрерывная
t
вместе со своей производной
на
t , a , b , f t –
отрезке
функция непрерывная на
;
.
25.
Еслиf x –
нечетная
функция,
то
a
f x dx 0
a
Если
.
f x –
a
a
a
0
четная
функция,
то
f x dx 2 f x dx .
3. Приложения определенных интегралов
1)
криволинейной
графиком
f x 0
Площадь
трапеции,
ограниченной
y f x
функции
x a; b ,
x a, x b
и
вычисляется по формуле
b
прямыми
осью
S f x dx
a
OX
26.
2)Площадь
плоской фигуры, ограниченной графиками
функций
y f1 x ,
:
y f 2 x
прямыми
x a,
f1 x f 2 x x a, b
x b
вычисляется
формуле:
b
S f 2 x f1 x dx
a
(рис.2)
и
по
27.
28.
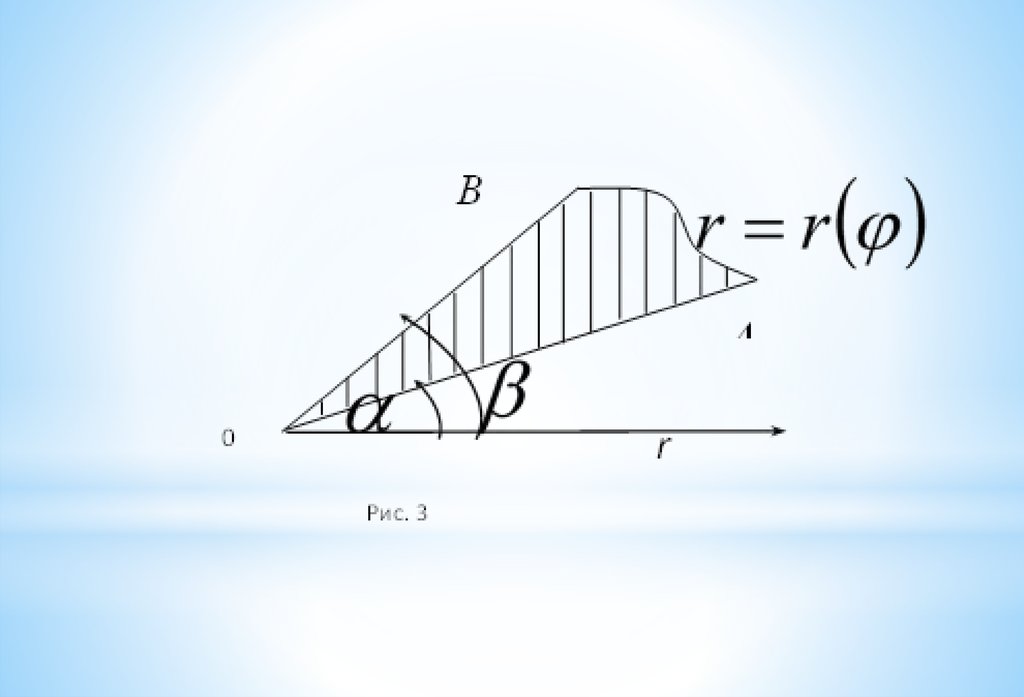
3)В
полярных
координатах
площадь
криволинейного
OAB , ограниченного кривой
сектора
r r
и
лучами
вычисляется по формуле:
,
1 2
S r d
2
(рис.3)
29.
30.
4)Если
тело
образовано вращением вокруг оси OX
криволинейной трапеции, то его объем
b
V f
2
x dx
a
При вращении
5)
OY
вокруг оси
криволинейной трапеции,
образуется тело вращения, объем которого
d
V g y dy
c
2
31.
6)кривая
l
Если
задана уравнением
, то длина ее дуги от точки
плоская
y y x
A a, y(a)
до
B
b
,
y
(
b
)
точки
вычисляется по формуле:
b
l 1 y ( x) dx
2
a
l
Если
задана параметрически:
x x t
t
;
, то длина ее
y y t , где
дуги вычисляется по формуле:
l
xt
2
yt dt
2
32.
lЕсли
задана в полярных координатах
уравнением r r , , то длина ее
дуги определяется по формуле:
l r r ( ) d
2
2
33.
xf
F
,
7) Работа переменной силы
x
f
– непрерывная функция на
где
a; b
OX
на
, действующей в направлении оси
b
a;
вычисляется по формуле:
отрезке
b
b
a
a
A dA f ( x)dx
34.
8) Если материальная точка движетсяv
v
t
прямолинейно со скоростью
, то
пройденный ею за промежуток времени от
t2
t1
до
t2
S v t dt
путь
t1
.




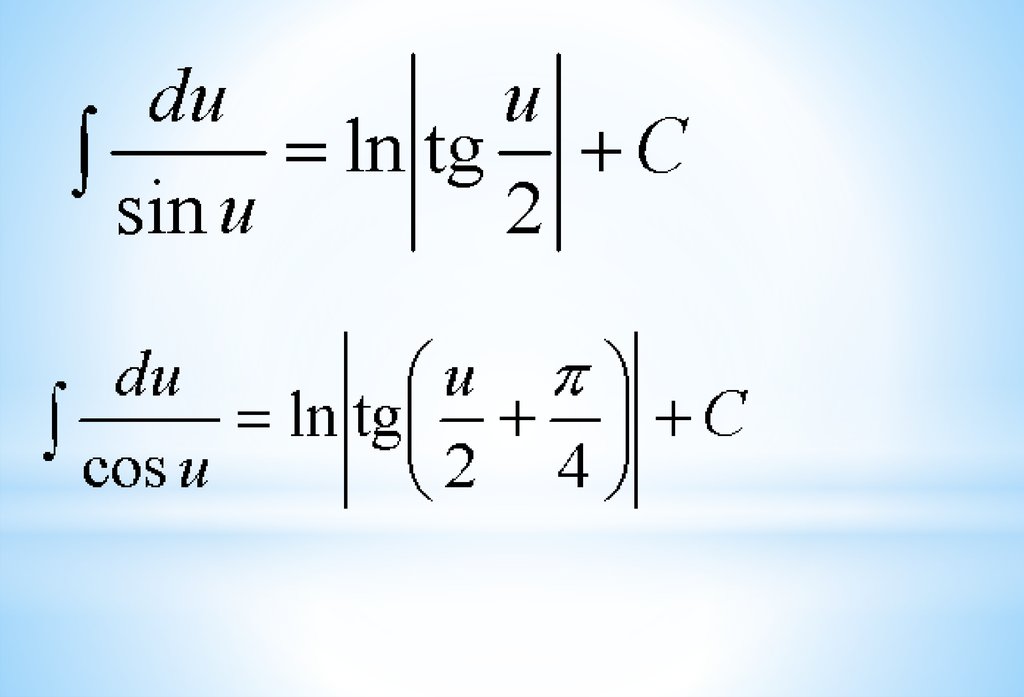




























 mathematics
mathematics








