Similar presentations:
Интегральное исчисление. Неопределенный интеграл
1. Интегральное исчисление
Неопределенный интеграл2. Неопределенный интеграл
Определение 1.Функция F (x ) называется
первообразной для f (x) в ( a, b) ,
если F (x ) определена в ( a, b) и
F ( x) f ( x)
Пример.
f ( x) sin x F ( x) cos x
( так как ( cos x) sin x )
3. Неопределенный интеграл
Теорема (о разности первообразных).F ( x) и G( x) первообраз
ные
для f ( x) в (a, b)
F ( x) G( x) const
Доказательство.
Обозначим через ( x) F ( x) G( x) .
Пусть x1 , x2 ( a, b ) .
Функция (x ) удовлетворяет
условиям теоремы Лагранжа:
а) ( x) непрерывна на x1 , x2
б) ( x) F ( x) G ( x)
f ( x) f ( x) 0 в ( x1 , x2 )
( x2 ) ( x1 ) (c)(x2 x1 ) 0
( x2 ) ( x1 ) x1 , x2 (a, b)
( x) const .
4. Неопределенный интеграл
Следствие.Пусть F (x ) первообразная для
Тогда любая другая первообразная
f (x) в ( a , b. ) .
G( x) F ( x) C
Определение 2.
Неопределенным интегралом от f (x)
называется совокупность всех первообразных
f ( x)dx F ( x) C
Графическая иллюстрация
y
Пример.
y F (x)
sin xdx cos x C
a
b
x
5. Неопределенный интеграл
Таблица основных интегралов.1.
F ( x) f ( x) F ( x)
-первообразная для f (x)
0dx C
2.
x n 1
x dx
C (n 1)
n 1
3.
dx
ln x C
x
4.
5.
n
e dx e
ax
a dx
C
ln a
x
x
x
C
Таблица производных.
(C ) 0
( xn ) n xn 1
(a x ) a x ln a
(e x ) e x
(ln x)
1
x
(log a x)
1
?
x ln a
6. Неопределенный интеграл
cos xdx sinx Csin xdx cos x C
(cosx) sin x
dx
tgx C
2
cos x
dx
ctgx C
sin 2 x
(tg x)
6.
7.
8.
9.
10.
x
arcsin C
a
a2 x2
11.
dx
1
x
arctg
C
2
2
a
a
a x
dx
( a const 0 )
1
cos2 x
7. Неопределенный интеграл
12.Длинный логарифм.
13.
14.
x2 a2
ln x x 2 a 2 C
Высокий логарифм.
dx
(
dx
1
a x
ln
C
2
2
2a a x
a x
dx
1
x a
ln
C )
x 2 a 2 2a x a
8. Неопределенный интеграл
Свойства неопределенных интегралов (правила интегрирования).f ( x)dx f ( x)
f ( x)dx f ( x)dx
1.
2.
3. Линейность неопределенного интеграла.
f ( x)dx f ( x) C
или
d
или
d f ( x) f ( x) C
( f ( x) g ( x))dx f ( x)dx g ( x)dx
C f ( x)dx C f ( x)dx
( C const 0 )
(k f (x) k g (x))dx
k f ( x)dx k g ( x)dx
1
1
2
2
( k1 , k2 const 0 )
9. Неопределенный интеграл
Доказательство формулы( f ( x) g ( x))dx f ( x) g ( x)
1.
2.
( f ( x) g ( x))dx f ( x)dx g ( x)dx
f ( x)dx g ( x)dx
f ( x)dx g ( x)dx f ( x) g ( x)
Ч.т.д.
10. Неопределенный интеграл
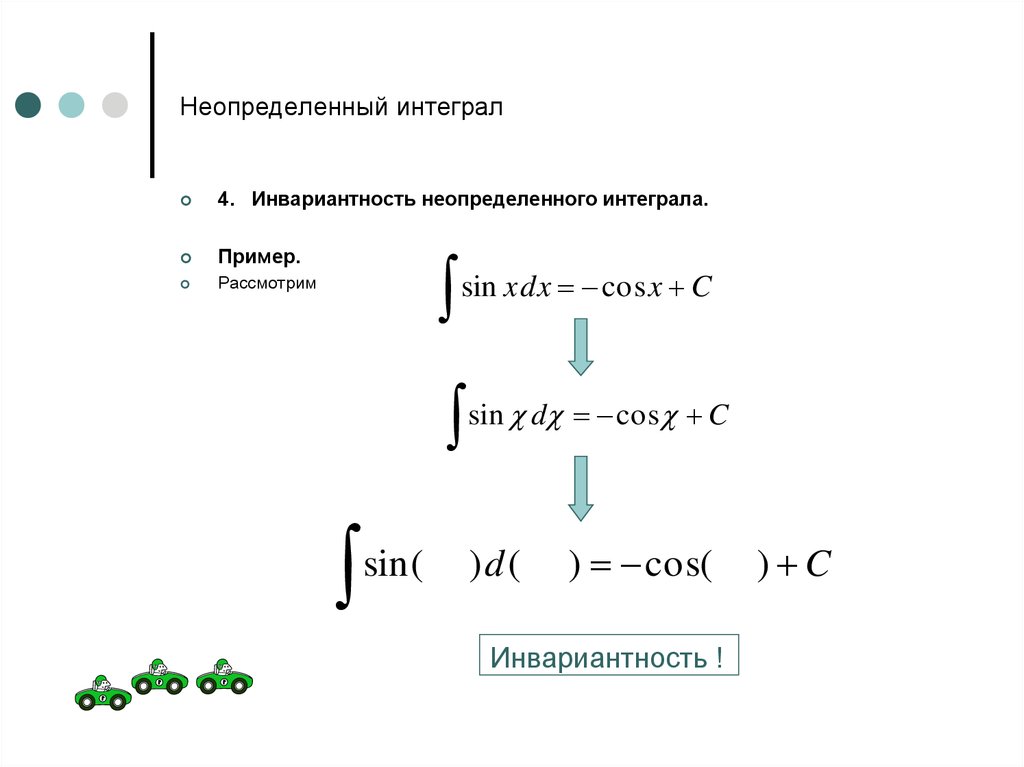
4. Инвариантность неопределенного интеграла.Пример.
Рассмотрим
sin x dx cos x C
sin(
sin d cos C
)d (
) cos(
Инвариантность !
) C
11. Неопределенный интеграл
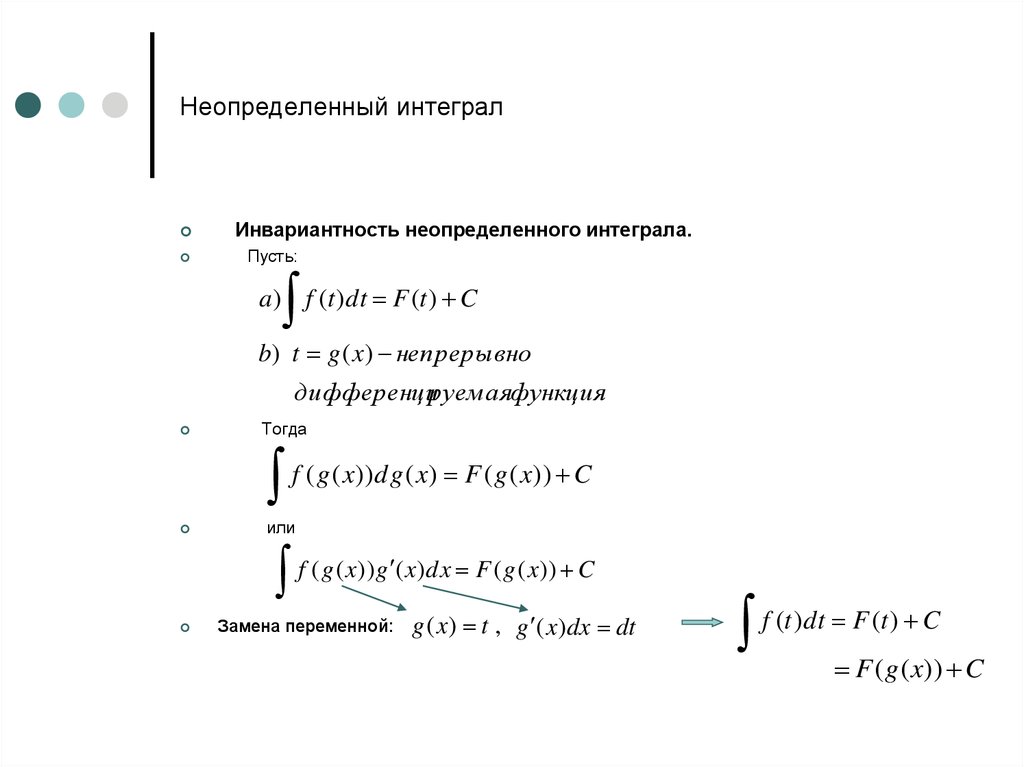
Инвариантность неопределенного интеграла.Пусть:
a) f (t )dt F (t ) C
b) t g ( x) непрерывно
дифференцируемаяфункция
Тогда
f ( g ( x))d g ( x) F ( g ( x)) C
или
f ( g ( x))g ( x)dx F ( g ( x)) C
Замена переменной:
g ( x) t , g ( x)dx dt
f (t)dt F (t) C
F ( g ( x)) C
12. Неопределенный интеграл
Доказательство.F ( g ( x)) F (t ) t g ( x) g ( x) f ( g ( x)) g ( x)
Пример.
sin 5 x cos xdx
t sin x dt cos xdx
t6
sin 6 x
t dt C
C
6
6
5
13. Неопределенный интеграл
5. Интегрирование по частям.u ( x) v ( x) dx u ( x) v( x) v( x) u ( x) dx
или
u d v u v v d u
14. Неопределенный интеграл
Пример.x sin xdx x d ( cos x)
u
v
x( cos x) ( cos x)dx
x cos x sin x C
15. Неопределенный интеграл
Интегрирование по частям.u ( x) v ( x) dx u ( x) v( x) v( x) u ( x) dx
Доказательство.
1.
2.
u ( x) v ( x) dx u ( x) v ( x)
u ( x) v( x) v( x) u ( x) dx
?
u ( x) v( x) v( x) u ( x) u ( x) v ( x)
u v u v u v
Ч.т.д.











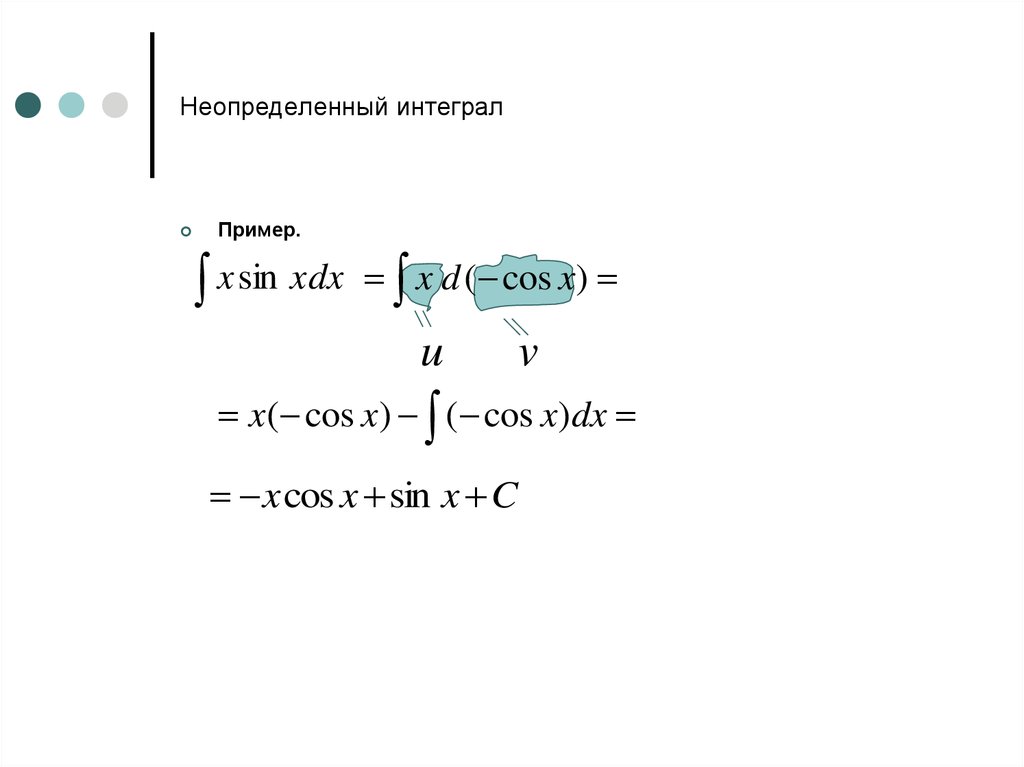

 mathematics
mathematics








