Интегральное исчисление. Неопределенный интеграл

1. Интегральное исчисление

Неопределенный интеграл

2. Неопределенный интеграл

Определение 1.
Функция F (x) называется первообразной для f (x) в ( a, b)
если F (x) определена в ( a, b) и
F ( x) f ( x)
Пример.
f ( x) sin x F ( x) cos x
( так как ( cos x) sin x )

3. Неопределенный интеграл

Теорема (о разности первообразных).
F ( x) и G ( x) первообразные
для f ( x) в (a, b)
F ( x) G( x) const
Доказательство.
Обозначим через ( x) F ( x) G( x) .
Пусть x , x ( a, b ) .
1
2
Функция
(x) удовлетворяет
условиям теоремы Лагранжа:
а) ( x) непрерывна на x , x
1
2
б)
( x) F ( x) G ( x)
f ( x) f ( x) 0 в ( x1 , x2 )
( x2 ) ( x1 ) (c)( x2 x1 ) 0
( x2 ) ( x1 ) x1 , x2 (a, b)
( x) const .

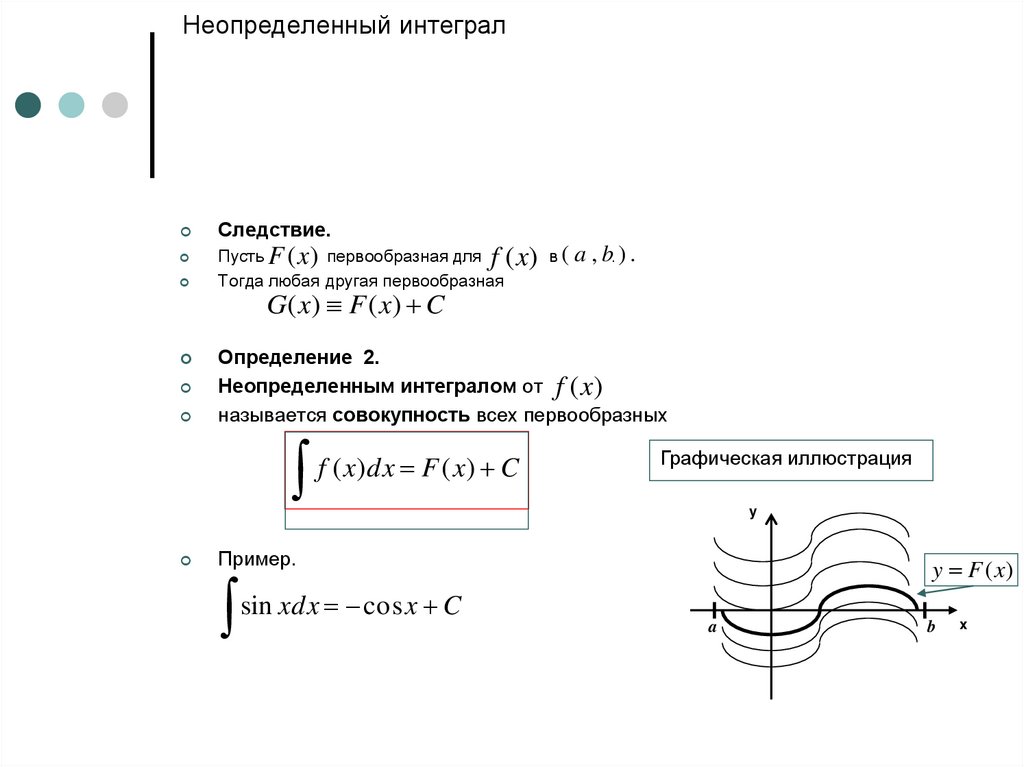
4. Неопределенный интеграл

Следствие.
Пусть F (x ) первообразная для
Тогда любая другая первообразная
f (x) в ( a , b. ) .
G ( x) F ( x) C
Определение 2.
Неопределенным интегралом от f (x)
называется совокупность всех первообразных
f ( x)dx F ( x) C
Графическая иллюстрация
y
Пример.
y F (x)
sin xdx cos x C
a
b
x

5. Неопределенный интеграл

Таблица основных интегралов.
1.
2.
x n 1
x dx
C (n 1)
n 1
3.
dx
ln x C
x
4.
5.
F ( x) f ( x) F ( x)
-первообразная для f (x)
0dx C
n
e dx e C
ax
a dx
C
ln a
x
x
x
Таблица производных.
(C ) 0
( xn ) n xn 1
(a x ) a x ln a
(e x ) e x
(ln x)
1
x

6. Неопределенный интеграл

6.
7.
8.
9.
10.
cosxdx sinx C
sin xdx cos x C
(cosx) sin x
dx
tgx C
2
cos x
dx
ctgx C
sin 2 x
(tg x)
a x
dx
2
11.
arcsin
2
x
C
a
dx
1
x
arctg
C
2
2
a
a
a x
( a const 0 )
1
cos2 x

7. Неопределенный интеграл

12.
Длинный логарифм.
x a
dx
2
13.
ln x x 2 a 2 C
2
Высокий логарифм.
dx
1
x a
ln
x 2 a 2 2a x a C
14.
(
dx
1
a x
ln
C)
2
2
2a a x
a x

8.

Примеры
a x
dx
2
arcsin
2
x
C
a
x2 a
ln x x a C
2
2
2
dx
1
x a
ln
x 2 a 2 2a x a C
4 x
arcsin
2
x
C
2
dx
1
x
arctg
C
25 x 2 5
5
dx
1
x
arctg
C
a2 x2 a
a
dx
dx
dx
x2 5
ln x x 2 5 C
dx
1
x 3
1 x 3
ln
C
ln
C
x2 9 2 3 x 3
6 x 3

9. Доказательство формулы № 3

dx
ln x C
x
Для доказательства воспользуемся определением
f ( x) dx F ( x) C это значит, что F ( x) f ( x)
F ( x) ln | x |,
1
f ( x)
x
Проверим, что F ( x) f ( x)
1
(ln x) , x 0
x
F ( x) (ln | x |)
(ln( x)) , x 0 1 ( 1) 1
x
x
f ( x)
1
x

10. Примеры

dx
x 3 1
x 2
1
3
x
dx
C
C 2 C
x3
3 1
2
x
Примеры
Формула: : x n dx x n 1 C
(n 1)
n 1
x 3 1
x4
x 3 1 C 4 C
3
dx
x 3 1
x 2
1
3
x
dx
C
C
C
x3
2
3 1
2
x
1
2
1
1
2
3
2
2
1
5
3
5
x
x
2 x3
x dx x dx 1 C 3 C 3 C
1
2
2
2
5
x
5 5 x3
5 2 x dx 2 C 3 C 3 C
x
1
5
5
dx
x

11. Неопределенный интеграл

Свойства неопределенных интегралов (правила интегрирования).
f ( x)dx f ( x)
d
f ( x)dx f ( x)dx
1.
2.
d F ( x) F ( x) C или
3. Линейность неопределенного интеграла.
или
F ( x) dx F ( x) C
( f ( x) g ( x))dx f ( x)dx g ( x)dx
C f ( x)dx C f ( x)dx
( C const 0 )
(k f ( x) k g ( x))dx
k f ( x)dx k g ( x)dx
1
1
2
2
( k1 , k 2 const 0 )

12. Доказательство 1, 2 свойств

1). Докажем свойство 1.
f ( x)dx f ( x)
f ( x) dx ( F ( x) C ) f ( x)
2). Докажем свойство 2.
d F ( x) F ( x) C
d F ( x) F ( x) dx F ( x) C

13. Неопределенный интеграл

Доказательство формулы
1.
( f ( x) g ( x))dx f ( x)dx g ( x)dx
( f ( x) g ( x))dx f ( x) g ( x)
f ( x)dx g ( x)dx
f ( x)dx g ( x)dx f ( x) g ( x)
2.
Ч.т.д.

14. Примеры

1.
2.
3.
( 5x 4 )dx

15. Решение

1 1
2
x
5
x
1. (5 x 4)dx 5 xdx 4dx 5 xdx 4 dx 5
4x C
4x C
1 1
2
2.
3.
dx
x 3 1
x 2
1
3
x
dx
C
C
C
2
x3
3 1
2
2x
3
2
x xdx x dx
3
1
2
5
2
x
x
2 5
C
C
x C
3
5
5
1
2
2

16. Примеры

Интеграл от суммы равен сумме интегралов.
Постоянный множитель можно выносить за знак интеграла.
1
3
8x 7
8x
7
x
1
x dx
dx
dx
dx
8
dx
7
dx
8
x
dx
7
1
1
4).
3
3
3
x
x
x
x3
x3
1
2
3
1
1
3
2
1
3
2
3
5
3
2
3
1
3
x
x
x
x
3x
243 x 5 213 x 2
8 x dx 7
8
7 C 8 7
C
C
1
2
2
5
2
5
2
1
1
3
3
3
3
24 x3 x 2 213 x 2
C
5
2

17. Неопределенный интеграл

4. Инвариантность неопределенного интеграла.
Пример.
Рассмотрим
sin x dx cos x C
sin u du cosu C
sin(
)d (
) cos(
Инвариантность !
) C

18. Неопределенный интеграл

Инвариантность неопределенного интеграла.
Пусть:
a) f (t )dt F (t ) C
b) t g ( x) непрерывно
дифференцируемаяфункция
Тогда
f ( g ( x))d g ( x) F ( g ( x)) C
или
f ( g ( x))g ( x)dx F ( g ( x)) C
Замена переменной:
g ( x) t , g ( x)dx dt
f (t)dt F (t) C
F ( g ( x)) C

19. Доказательство.

F ( g ( x)) F (t ) t g ( x) g ( x) f ( g ( x)) g ( x)
f ( u )du F( u ) C
u 4x
1
1
1
1
sin
4
x
dx
sin
4
x
d
(
4
x
)
sin
udu
cos
u
C
cos 4 x C
du 4dx 4
4
4
4
2 x
e
dx
2 x 5
e dx
1 2 x
1 u
1 u
1 2 x
e
d(
2
x
)
u
2
x
e
du
e
C
e C
2
2
2
2
1 2 x 5
1 u
1 u
1 2 x 5
e
d(
2
x
5
)
u
2
x
5
e
du
e
C
e
C
2
2
2
2

20. Таблица интегралов может быть записана для произвольной функции u вместо аргумента x:

Подставим u вместо x:
du u C
u n 1
u du n 1 C
du
u ln | u | C
u
u
e
du
e
C
n
( n 1)
au
a du ln a C (a 0, a 1)
sin udu cosu C
u
cosudu sin u C
du
cos2 u tg u C
du
sin 2 u ctg u C

21. Продолжение таблицы интегралов для функции u вместо x

du
u
arcsin
C
2 2
a
a u
du
1
u
u 2 a 2 a arctg a C
du
2
2
ln
|
u
u
a
| C
2 2
u a
du
1 u a
u 2 a 2 2a ln u a C

22. При решении используется таблица дифференциалов. Основная формула:

y dx d( y )
2xdx d( x 2 )
3 x 2 dx d( x 3 )
4 x dx d( x )
3
4
e x dx d( e x )
1
dx d( l n x )
x
sin xdx d(cos x )
co s xdx d(sin x )
1
dx d( tg x )
2
cos x
1
dx d( ctg x )
2
sin x
1
1 x
2
dx d(arcsin x ) d(arcco s x )
1
dx d(arctg x ) d(arcctg x )
2
1 x

23.

u6
sin6 x
sin xcos xdx sin xd(sin x ) u sin x u du 6 C 6 C
5
5
co s xdx d(sin x )
5

24. Интегрирование по частям

u dv u v v du

25. Неопределенный интеграл

u dv uv v du
xsin xdx x( cos x) ( cos x)dx
u x
dv sin x dx
du u dx dx v sin x dx cos x
x cos x sin x C

26. Пример 2

ln x
x3 dx
u ln x,
dv
dx
x3
1
dx
1
3
du ln x dx dx, v 3 x dx 2
x
x
2x
ln x 1 dx
ln x 1 1
ln x
1
2 3 2 2 C C 2 2
2x
2 x
2x
2 2x
2x 4x