Similar presentations:
Дифференциальные уравнения
1. Дифференциальные уравнения
Общее и частное решение.Алгоритм решения дифференциальных
уравнений первого порядка с
разделяющимися переменными.
2. Дифференциальным уравнением называется уравнение содержащее независимую переменную х, искомую функцию у и ее производные.
f ( y; x; y ; y ;...; y ) 0,
,,
( n)
Примеры:
y x 0 (диф. уравнение 1 го порядка ).
y x y 0 (диф. уравнение 2 го порядка )
Порядок диф. уравнения определяется по порядку высшей производной.
3.
Решением дифференциального уравненияназывается функция, которая обращает
данное диф. уравнение в тождество.
Пример:
Рассмотрим дифференциальное уравнение первого порядка
x y 5 0
Решением этого уравнения является функция
Найдем y’ и подставим в уравнение.
5y
x 5 0
x
Значит
y 5 Lnx
5 5 0
y 5 Lnx
5
y
x
- тождество
– есть решение этого диф. уравнения.
4.
Общимрешением
дифференциального
уравнения называется функция, зависящая от х и
от С, где С – произвольная константа, которая
обращает данное диффуравнение в тождество.
f(x,C).
Пример:
y 2x C
Частным
решением
дифференциального
уравнения называется решение, полученное из
общего при фиксированном С. f(x).
Пример:
y 2x 7
5.
Дифференциальное уравнение 1-го порядканазывается уравнением с разделяющимися
переменными, если его можно представить в
виде:
f ( y )dy g ( x)dx
f ( y)
Примеры:
1) x dx y dy 0
y dy x dx
x
dy
x |·dx
2) y
y
dx
y
dy y dx
dy
y
dx
g ( x)
x
dy dx |·y
y
y dy x dx
6. Алгоритм решения диф.уравнений 1-го порядка с разделяющимися переменными.
dy• Производную представить в виде частного
дифференциалов
dx
• Каждое слагаемое записать в отдельной части
уравнения.
• Каждую переменную собрать в той части
уравнения, где её дифференциал стоит в
числителе. (Разделить переменные)
• Проинтегрировать обе части уравнения, найти
общее решение.
• Если заданы начальные условия, найти значение
константы и записать частное решение.
7. Пример 1. Найти частное решение диф.уравнения:
22 y y 1 3x если y0 3
dy
2 y 1 3x 2
dx
dx
2 y dy (1 3x )dx
2
при
x0 1
y2
2
2
y
dy
2
y
2
x3
3
(1
3
x
)
dx
x
3
x
x
3
2
2
2
y
dy
(1
3
x
)dx
y 2 x x3 C
- общее решение
Подставим начальные значения:
y x x 9
2
3
32 1 13 C
- частное решение
C 9
8. Пример 2. Найти частное решение диф.уравнения:
7 e3 x1 3x
y e 0
1 y
2
если
y0 1
при
7 e3 x dy 1 3 x dx
e
1 y dx 2
7 e3 x
1 3x
3x
dy e dx : (7 e )
1 y
2
3x
1
e
dy
dx
3x
1 y
2(7 e )
1
e3 x
1 y dy 2(7 e3x ) dx
x0 0
9.
1e3 x
1 y dy 2(7 e3x ) dx
3x
3x
3x
1
e
1 e dt
e
dx
1)
dx
3x
3x
3x
2 7 e
2 t 3e
2(7 e )
t 7 e
3x
3x
dt d (7 e ) (7 e ) dx 3e dx
dt
3x
dx 3 x
3e dx dt
3e
1 dt 1 dt 1
1
ln t C1 ln 7 e3 x C1
2 3t
6 t
6
6
3x
3x
1
2)
dy ln 1 y
1 y
10.
1ln 1 y ln 7 e3 x C1
6
C1 и ln C
C1 ln C
1
3x 6
ln 1 y ln 7 e
пробегают значения
ln C
1
3x 6
ln 1 y ln((7 e ) C )
1
3x 6
1 y (7 e ) C
y C 7 e 1
6
3x
- общее решение
( ; )
11.
y C 7 e 16
3x
- общее решение
y0 1
при
x0 0
1 C 6 7 e3 0 1
1 C 6 7 1 1
C6 8 2
2
C 6
8
2 6
y 6
7 e3 x 1
8
- частное решение
12. Линейные дифференциальные уравнения
Дифференциальноеуравнение
1-го
порядка называют линейными, если его
можно представить в виде у’ +P(x)y =Q(x),
где Р(x) и Q(x)-некоторые функции
переменной x, которые, в частности, могут
быть константами.
13.
Линейное диф.уравнение приводится куравнению с разделяющимися переменными
подстановкой у=u∙v ,
u и v-некоторые новые функции переменной x,
одна из которых подбирается таким образом,
чтобы множитель другой был равен 0.
dy y dx (u v) dx (u v v u )dx (
vdu udv
y u v
dy vdu udv
du
dv
v u )dx
dx
dx
14. Пример 3. Найти частное решение диф.уравнения:
(1 x 2 ) y x y 2 xy0 1
если
при
x0 3
(1 x 2 ) y x y 2 x : (1 x 2 )
x
2x
y
y
2
2
1 x
1 x
P( x)
Линейное уравнение
Q( x)
dy
x
2x
y
dx
2
2
dx 1 x
1 x
xdx
2x
dy
y
dx
2
2
1 x
1 x
15.
Выполним подстановкуy (u v )
dy vdu udv
xdx
2x
y
dx
dy
2
2
1 x
1 x
xdx
2x
vdu u (dv
v)
dx
2
2
1 x
1 x
0
xdx
dv
v 0
2
1 x
xdx
dv
v :v
2
1 x
16.
dvxdx
v
1 x2
xdx
1 x2
dt 1 dt 1
1
2
2
ln
1
x
2t 2 t 2 ln t 2 ln(1 x )
t 1 x
2
dt (1 x ) dx 2 xdx
2
dv
v ln v
dt
xdx
2
ln v ln 1 x2
v 1 x
2
17.
xdx2x
vdu u (dv
v)
dx
2
2
1 x
1 x
0
2
v 1 x
2x
1 x du u 0
dx
2
1 x
2
2x
2
:
1
x
1 x du
dx
2
1 x
2x
du
dx
(1 x 2 ) 1 x 2
2x
du
dx
1
2
2 2
(1 x ) (1 x )
2
18.
du (1 x )2x
2
2x
(1 x )
2
3
dx
2
3
dx
2
dt
t
3
2
3
2
t dt
t 2 1 2x 2 2
1
2
2
t
1
x
dt
t 2 (1 x ) dx 2 xdx
du u
u
2
1 x2
C
t
3
1
2
3
1
2
2t
1
2
19.
v 1 xu
2
y u v
y 1 x (
2
2
1 x
y 2 C 1 x
y0 1
1 2 C 1 3
2
2
1 x2
C
C)
- общее решение
при
2
y 2 1,5 1 x
2
x0 3
C 1,5
2
- частное решение
20. Однородное дифференциальное уравнение 1-го порядка.
Многочлен называется однородным относительнопеременных x, у, если все его слагаемые содержат одну
и ту же степень этих переменных.
5x y 7 x y 9 x
2
3
4
5
- однородный 5-ой степени
4 x7 y 7 97
- не однородный
a 4b 2 64 a 3b3 a 5b
- однородный 6-ой степени
21.
Дифференциальное уравнение первогопорядка называют однородным
дифференциальным уравнением, если его можно
привести к виду:
P( x, y )dy Q( x, y )dx,
где P(x,y) и Q(x,y) однородные многочлены
одинаковой степени
Примеры:
( x 2 y x y 2 )dy ( x3 y 3 )dx - однородное диф. ур.
однородное 3 степени
( x 2 y x y 2 )dy ( x 2 y 2 )dx - не однородное диф. ур.
Одн. 3 ст.
Одн. 2 ст.
22. Однородное диф.уравнение приводится к уравнению с разделяющимися переменными подстановкой у=z∙x, где z-некоторая функция
переменной x.dz
dy y dx ( z x) dx ( z x x z )dx ( x z )dx
dx
dz
xdx zdx xdz zdx
dx
y z x
dy xdz zdx
23. Пример 4. Найти частное решение диф.уравнения:
2x y y x 2 y 2если
y0 2
при
x0 1
dy
2
2
2 xy x y dx
dx
2 xydy ( x 2 y 2 )dx
Выполним подстановку
однородное 2 степени
y (z x )
dy ( xdz zdx)
2x y dy (x y )dx
2
2
2 x z ( xdz zdx) x (1 z )dx
2
2
2
24.
2 zxdz 2 z dx (1 z )dx2
2
2 zxdz (1 z )dx 2 z dx
2
2
2 zxdz (1 z 2 2 z 2 )dx
2 z x dz (1 z )dx : x
2
(1 z 2 )
2 zdz
dx
x
1
2z
(1 z 2 ) dz x dx
: (1 z )
2
уравнение с разделенными
переменными
25.
dt2z
2
dz
ln
t
ln
1
z
(1 z 2 ) t
t 1 z2
2
dt (1 z ) dz 2 zdz
2zdz dt
1
x dx ln x C1
ln 1 z ln x ln C
2
C1 lnC
ln 1 z ln C ln x
2
C
ln 1 z ln
x
2
C
1 z
x
2
26.
C1 z
x
y x z
y
z
x
2
2
y C
1
x
x
x
2
y xC x
x y xC
2
2
2
y 2 x2 xC
y0 2
при
- общее решение
x0 1
C 3
22 12 1 C
y x 3x
2
2
2
- частное решение
27. Задания
Найдите общее решение дифференциальногоуравнения:
1) sin x cos y y sin y cos x 0
2
2) x y 2 y x
2
2















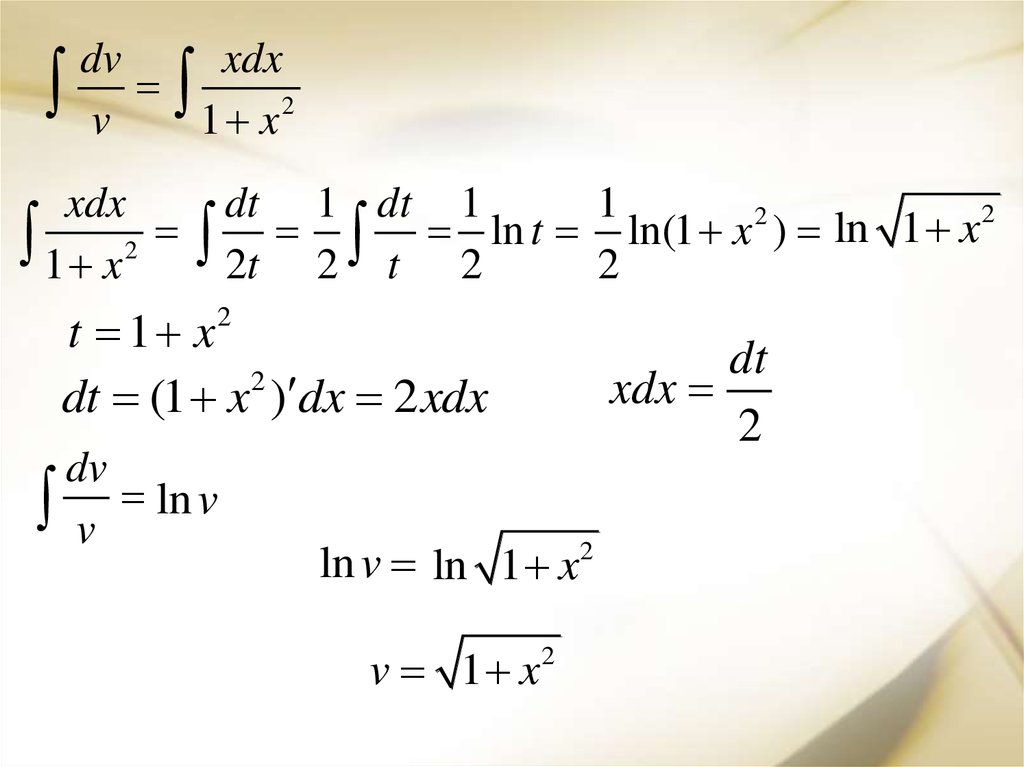








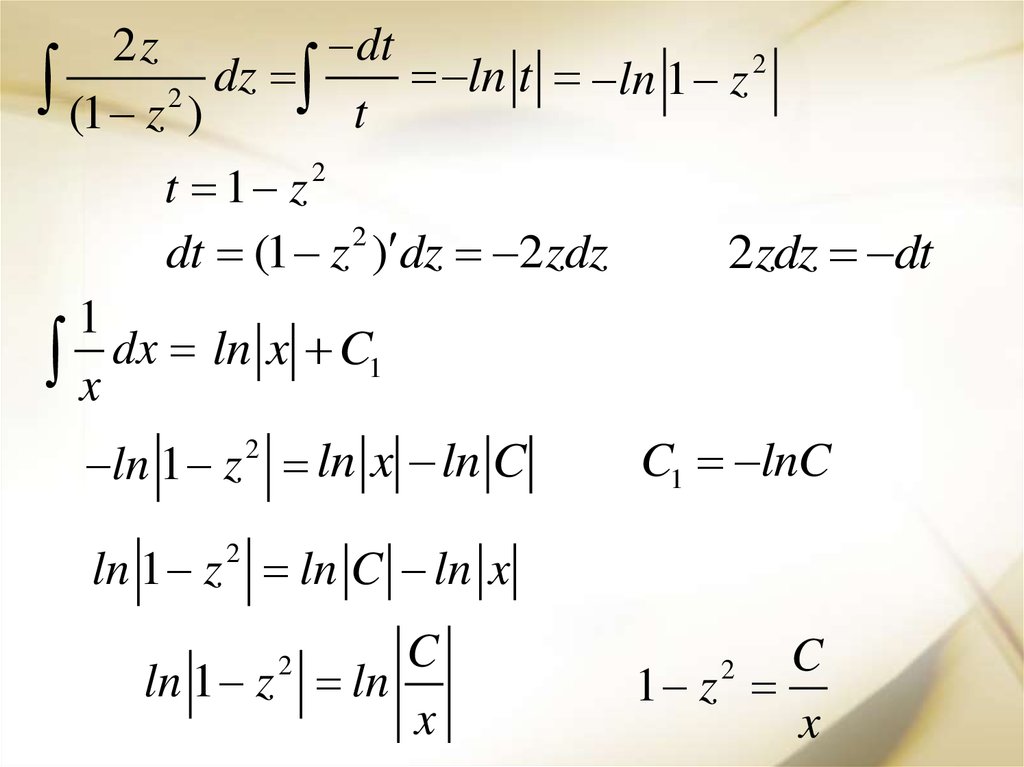


 mathematics
mathematics








