Математические модели систем автоматического управления

1. ТЕМА 6 МАТЕМАТИЧЕСКИЕ МОДЕЛИ СИСТЕМ АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ

Тема 6. «Математические модели САУ»
ТЕМА 6
МАТЕМАТИЧЕСКИЕ
МОДЕЛИ СИСТЕМ
АВТОМАТИЧЕСКОГО
УПРАВЛЕНИЯ

2. Математическую модель САУ используют

Тема 6. «Математические модели САУ»
Математическую модель САУ
используют
для изучения работы систем
автоматического регулирования при
установившемся режиме работы, а
также в переходных режимах.

3. Дифференциальное уравнение САУ

Тема 6. «Математические модели САУ»
Дифференциальное уравнение САУ
Динамику линейных автоматических систем
исследуют на основе неоднородных
дифференциальных уравнений n-го порядка с
постоянными коэффициентами:
n
n 1
2
d y
d y
d y
dy
a0 n a1 n 1 an 1 2 an
dt
dt
dt
dt
d mх
d m 1 х
d 2х
dх
b0 m b1 m 1 bm 1 2 bm
dt
dt
dt
dt
ai, bi - постоянные коэффициенты,
у – управляемая (выходная) величина,
х – входная величина.
Уравнение описывает динамический процесс изменения
выходной величины при наличии возмущающих воздействий.

4. Дифференциальное уравнение САУ

Тема 6. «Математические модели САУ»
Дифференциальное уравнение САУ
В операторной форме это уравнение:
D( p) y M ( p) x;
D( p) a0 p a1 p
n
d
dt
n 1
M ( p) b0 p b1 p
m
an ;
m 1
bm ,
d
p=
- оператор дифференцирования
dt
D(p) – оператор левой части
М(р) – оператор правой части

5. Дифференциальное уравнение САУ

Тема 6. «Математические модели САУ»
Дифференциальное уравнение САУ
Часто используют понятие передаточной
функции, выражение которой получают:
M ( p) b0 p bm
W ( p)
n
D( p) a0 p an
m
Передаточная функция – это отношение операторов правой
и левой частей дифференциального уравнения. Знаменатель
передаточной функции определяет характеристическое
уравнение для исходного уравнения, с помощью которого
описывают свободные движения (например, колебания)
системы.

6. Преобразование Лапласа

Тема 6. «Математические модели САУ»
Для решения дифференциального уравнения системы используют
метод анализа, основанный на преобразованиях Лапласа.
Суть в том, что функция вещественных переменных заменяется ее
изображением, связь между которыми осуществляется через оператор
Лапласа:
pt
F ( p) e
f (t )dt
0
F(p) – изображение функции
p=
d
dt
- оператор дифференцирования или оператор Лапласа
f(t) – функция вещественного переменного
Такая замена позволяет свести решение дифференциальных уравнений к
простейшим алгебраическим операциям для нахождения изображения.
А зная изображение, можно найти искомую функцию по специальным
формулам:

7. Преобразование Лапласа

Тема 6. «Математические модели САУ»
f (t ) F ( p)
f n (t ) p n F ( p)
1
F(p) , то f (t ) 1
p
F(p) a( p 2 a 2 ), то f (t ) sin( at )
1
F(p)
, то f (t ) e t
p
F(p)
p( p )
, то f (t ) 1 e t

8. Преобразование Лапласа

Тема 6. «Математические модели САУ»
Применив преобразование Лапласа к дифференциальному уравнению,
получим связь изображений входной и выходной функций:
y( p) b0 p bm
W ( p)
x( p) a0 p n an
m
Откуда дифференциальное уравнение будет иметь вид:
y ( p ) W ( p ) x( p )
Передаточная функция будет иметь вид:
y ( p)
W ( p)
x( p )

9. Амплитудно-фазовая частотная (АФЧ) характеристика системы

Тема 6. «Математические модели САУ»
Амплитудно-фазовая частотная (АФЧ)
характеристика системы
Если в выражение передаточной функции подставить вместо
оператора р мнимую переменную jw , то полученное уравнение
y ( jw )
W ( jw )
x( jw )
определяет амплитудно-фазовую частотную характеристику системы

10. Линейные системы

Тема 6. «Математические модели САУ»
Линейные системы
Для линейных систем передаточная функция исчерпывающе
характеризует поведение системы при любых возмущениях, так как
значение W(p) не зависит от формы возмущения.
Если принять в качестве внешнего воздействия функцию f(t)=1, т.е.
изображение функции х(р)=1/р, (соответствует единичному скачку
внешней нагрузки - мгновенное приложение нагрузки), то изображение
выходной величины имеет вид:
W ( p)
у ( р)
p
Т.О. зная передаточную функцию системы, можно получить изображение
управляемой величины и по формулам преобразования Лапласа перейти к
динамической характеристике звена или системы.
ЕСЛИ ЗНАМЕНАТЕЛЬ ПЕРЕДАТОЧНОЙ ФУНКЦИИ W(p)
ПРИРАВНЯТЬ К 0, ТО ПОЛУЧИМ ХАРАКТЕРИСТИЧЕСКОЕ
УРАВНЕНИЕ, ОПИСЫВАЮЩЕЕ ЕЕ СВОБОДНОЕ ДВИЖЕНИЕ, Т.Е.
МАТЕМАТИЧЕСКУЮ МОДЕЛЬ СИСТЕМЫ.

11. ПРИМЕР:

Тема 6. «Математические модели САУ»
ПРИМЕР:
Пусть передаточная функция имеет вид: W ( р)
1
Тр 1
Получить уравнение для выходного параметра y(t).
РЕШЕНИЕ:
W ( p)
1
y( р)
р
p(Tp 1)
1
1
T
1
1 p( p )
Tp p p p
T
T
Поскольку изображение функции изменения выходного параметра имеет
полученный вид, то сама функция имеет вид:
y (t ) 1 e
t

12. Замечание

Тема 6. «Математические модели САУ»
Замечание
Для получения математической модели автоматической
системы необходимо все реальные элементы в системе
заменить типовыми динамическими звеньями, преобразовав
функциональную блок-схему в структурную схему системы,
которая представляет собой соединение типовых
динамических звеньев. Для структурной схемы требуется
получить передаточную функцию системы и, приравняв
знаменатель W(p) к 0, получить характеристическое
уравнение системы или ее математическую модель.

13. Типовые динамические звенья и способы их соединения.

Тема 6. «Математические модели САУ»
Типовые динамические звенья и способы их соединения.
Типовое динамическое звено – часть автоматической
системы, динамические свойства которого описываются
дифференциальным уравнением не выше второго порядка.
ЛЮБОЕ ДИНАМИЧЕСКОЕ ЗВЕНО ХАРАКТЕРИЗУЕТСЯ
1.
2.
3.
ДИФФЕРЕНЦИАЛЬНЫМ УРАВНЕНИЕМ ЗВЕНА
ПЕРЕДАТОЧНОЙ ФУНКЦИЕЙ
АМПЛИТУДНО-ФАЗОВОЙ ЧАСТОТНОЙ ХАРАКТЕРИСТИКОЙ
Различают:
1. Безынерционные звенья
2. Инерционные звенья
3. Колебательные звенья
4. Дифференцирующие звенья
5. Интегрирующие звенья.

14. БЕЗЫНЕРЦИОННЫЕ ЗВЕНЬЯ.

Тема 6. «Математические модели САУ»
БЕЗЫНЕРЦИОННЫЕ ЗВЕНЬЯ.
Звенья у которых при скачкообразном изменении
входного сигнала, выходной изменяется в k раз.
ДИФФЕРЕНЦИАЛЬНОЕ УРАВНЕНИЕ (ДУ): y kx
k – коэффициент статического преобразования или коэффициент преобразования
ПЕРЕДАТОЧНАЯ ФУНКЦИЯ (ПФ):
y ( p) kx( p)
y ( p)
W ( p)
k
x( p )
АФЧ-ХАРАКТЕРИСТИКА (АФЧХ):
W (iw ) k

15. БЕЗЫНЕРЦИОННЫЕ ЗВЕНЬЯ.

Тема 6. «Математические модели САУ»
БЕЗЫНЕРЦИОННЫЕ ЗВЕНЬЯ.
К безынерционным звеньям можно отнести передаточные
механизмы, усилители, насосы и др.
w1
ПРИМЕР:
w2
x
Механическая передача
V wr
w1r1 w2r2
r1
w 2 w1 kw1
r2
y
r2
r1
V
- ПЕРЕДАТОЧНАЯ ФУНКЦИЯ (ПФ)
Для насоса x – атмосферное давление, у – давление, создаваемое насосом.

16. ИНЕРЦИОННЫЕ ЗВЕНЬЯ.

Тема 6. «Математические модели САУ»
ИНЕРЦИОННЫЕ ЗВЕНЬЯ.
при скачкообразном изменении входного сигнала,
выходной сигнал стремиться к новому установившемуся
значению по экспоненциальному закону.
ДИФФЕРЕНЦИАЛЬНОЕ УРАВНЕНИЕ (ДУ):
ПЕРЕДАТОЧНАЯ ФУНКЦИЯ (ПФ):
dy
T
y kx
dt
Tpy ( p) y ( p) kx( p)
k
W ( p)
Tp 1
АФЧ-ХАРАКТЕРИСТИКА (АФЧХ):
W ( jw )
k
T jw 1

17. ИНЕРЦИОННЫЕ ЗВЕНЬЯ.

Тема 6. «Математические модели САУ»
ИНЕРЦИОННЫЕ ЗВЕНЬЯ.
К инерционным звеньям можно отнести баки с жидкостью,
электродвигатели пост. тока, генераторы (при определенных
допущениях), термопары, электрические цепи R-C и др.
R
ПРИМЕР:
электрическая цепь R-C
C
UВЫХ
U i
По II закону Кирхгоффа составим
уравнение электрической цепи
i C
iR U ВЫХ U
dU ВЫХ
RC
U ВЫХ U
dt
dy
T
y kx
dt
dU ВЫХ
dt
y
RC T
y 1 e
t
T
t
1 e
t
RC

18. КОЛЕБАТЕЛЬНЫЕ ЗВЕНЬЯ.

Тема 6. «Математические модели САУ»
КОЛЕБАТЕЛЬНЫЕ ЗВЕНЬЯ.
при скачкообразном изменении входного сигнала, выходной
сигнал колеблется относительного нового установившегося
значения (положения равновесия) с амплитудой, затухающей по
экспоненциальному закону.
ДИФФУР (ДУ):
2
d
y
dy
2
T2
T1 y kx
2
dt
dt
ПЕРЕДАТОЧНАЯ ФУНКЦИЯ (ПФ):
k
W ( p) 2 2
T2 p T1 p 1
АФЧ-ХАРАКТЕР. (АФЧХ):
k
W ( jw ) 2
2
T2 jw T1 jw 1
Т1 – коэффициент, характеризует демпфирование (диссипативные силы),
Т2 – коэффициент, характеризует раскачивающие свойства в системе

19. КОЛЕБАТЕЛЬНЫЕ ЗВЕНЬЯ.

Тема 6. «Математические модели САУ»
КОЛЕБАТЕЛЬНЫЕ ЗВЕНЬЯ.
К колебательным звеньям можно отнести объекты, имеющие
подпружиненную массу, т.е. имеющие упругость
L
R
ПРИМЕР:
Колебательный контур R-L-C
По II закону Кирхгоффа составим
уравнение электрической цепи
L
U
i
di
iR U ВЫХ U
dt
d 2U ВЫХ
dU ВЫХ
LC
RC
U ВЫХ U
2
dt
dt
RC T1
C
i C
UВЫХ
dU ВЫХ
dt
y
LC T2
2
d
y
dy
T22 2 T1 y kx
dt
dt
t

20. ДИФФЕРЕНЦИРУЮЩИЕ ЗВЕНЬЯ.

Тема 6. «Математические модели САУ»
ДИФФЕРЕНЦИРУЮЩИЕ ЗВЕНЬЯ.
Выходной сигнал пропорционален скорости
изменения входного сигнала.
ДИФФУР (ДУ):
dy
dx
T
y k
dt
dt
dx
y k
dt
ДЛЯ ИДЕАЛЬНОЙ СХЕМЫ
ДЛЯ РЕАЛЬНОЙ СХЕМЫ СУЩЕСТВУЕТ ИНЕРЦИОННОЕ ЗВЕНО
(КОТОРОМУ СООТВЕТСТВУЕТ ПЕРВОЕ СЛАГАЕМОЕ)
ПЕРЕДАТОЧНАЯ ФУНКЦИЯ (ПФ):
W ( p) kp
АФЧ-ХАРАКТЕР. (АФЧХ):
W ( jw ) k jw
Примером являются: тахогенераторы, цепь R-C с усилителем

21. ИНТЕГРИРУЮЩИЕ ЗВЕНЬЯ.

Тема 6. «Математические модели САУ»
ИНТЕГРИРУЮЩИЕ ЗВЕНЬЯ.
звено, в котором выходная величина пропорциональна интегралу
по времени входной величины или скорость изменения выходного
сигнала пропорциональна входному сигналу.
t
ДИФФУР (ДУ): y k xd
ИЛИ
0
dy
kx
dt
ИДЕАЛЬНАЯ
СХЕМА
d 2 y dy
TИ 2 kx реальная схема, TИ – время разгона
dt
dt
ПЕРЕДАТОЧНАЯ ФУНКЦИЯ (ПФ):
k
W ( p)
p
АФЧ-ХАРАКТЕР. (АФЧХ):
k
W ( jw )
jw
Примером являются: конденсатор, гидроцилиндр, пневмоцилиндр и др.

22. СОЕДИНЕНИЯ ЗВЕНЬЕВ

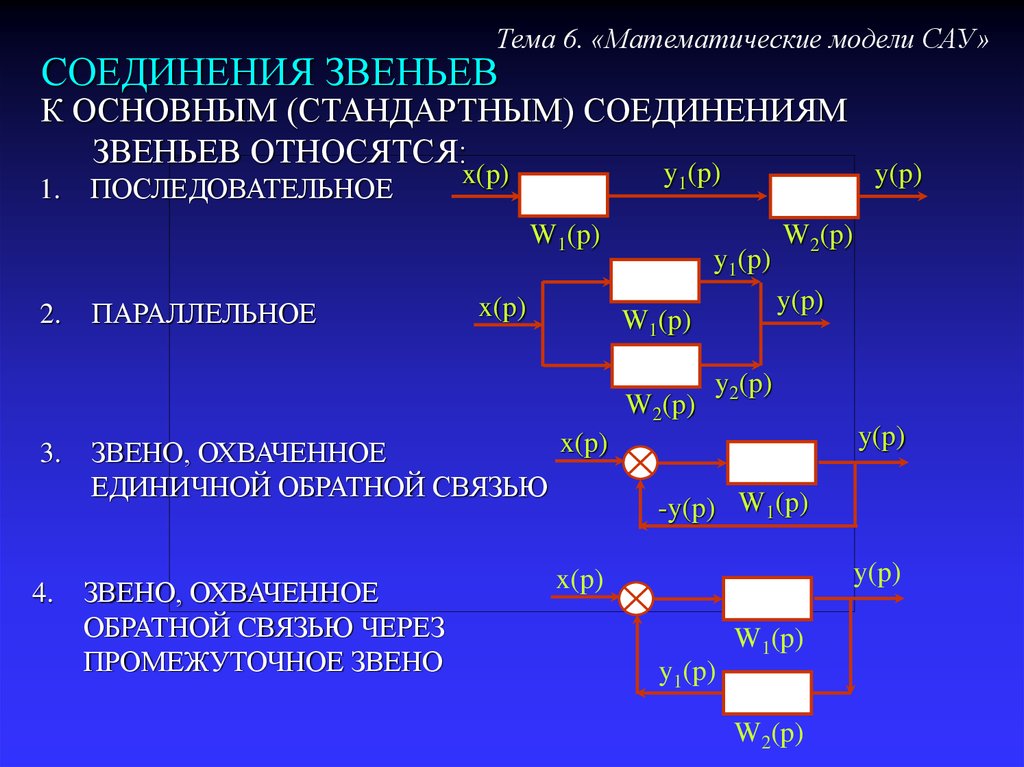
Тема 6. «Математические модели САУ»
СОЕДИНЕНИЯ ЗВЕНЬЕВ
К ОСНОВНЫМ (СТАНДАРТНЫМ) СОЕДИНЕНИЯМ
ЗВЕНЬЕВ ОТНОСЯТСЯ:
1.
ПОСЛЕДОВАТЕЛЬНОЕ
y1(p)
x(p)
W1(p)
2.
ПАРАЛЛЕЛЬНОЕ
x(p)
y1(p)
3.
4.
x(p)
ЗВЕНО, ОХВАЧЕННОЕ
ЕДИНИЧНОЙ ОБРАТНОЙ СВЯЗЬЮ
ЗВЕНО, ОХВАЧЕННОЕ
ОБРАТНОЙ CВЯЗЬЮ ЧЕРЕЗ
ПРОМЕЖУТОЧНОЕ ЗВЕНО
W2(p)
y(p)
W1(p)
W2(p)
y(p)
y2(p)
y(p)
-y(p) W1(p)
y(p)
x(p)
W1(p)
y1(p)
W2(p)

23. ПОСЛЕДОВАТЕЛЬНОЕ СОЕДИНЕНИЕ

Тема 6. «Математические модели САУ»
ПОСЛЕДОВАТЕЛЬНОЕ СОЕДИНЕНИЕ
ОПРЕДЕЛИТЬ ПЕРЕДАТОЧНУЮ ФУНКЦИЮ
y1(p)
x(p)
W1(p)
y(p)
W2(p)
y( p) W2 ( p) y1 ( p)
y1 ( p) W1 ( p) x( p)
y( p) W2 ( p) y1 ( p) W2 ( p) W1 ( p) x( p)
W ( p) W2 ( p) W1 ( p)

24. ПАРАЛЛЕЛЬНОЕ СОЕДИНЕНИЕ

Тема 6. «Математические модели САУ»
ПАРАЛЛЕЛЬНОЕ СОЕДИНЕНИЕ
ОПРЕДЕЛИТЬ ПЕРЕДАТОЧНУЮ ФУНКЦИЮ
y1(p)
x(p)
W1(p)
W2(p)
y1 ( p) W1 ( p) х( p)
y(p)
y2(p)
y2 ( p) W2 ( p) х( p)
y( p) y1 ( p) y1 ( p) x( p) W2 ( p) W1 ( p)
W ( p) W2 ( p) W1 ( p)

25. ОХВАЧЕННОЕ ЕДИНИЧНОЙ ОБРАТНОЙ СВЯЗЬЮ

Тема 6. «Математические модели САУ»
ОХВАЧЕННОЕ ЕДИНИЧНОЙ ОБРАТНОЙ СВЯЗЬЮ
ОПРЕДЕЛИТЬ ПЕРЕДАТОЧНУЮ ФУНКЦИЮ
x(p)
y(p)
-y(p)
W1(p)
y( p) W1 ( p) x( p) y( p)
W1 ( p)
W ( p)
1 W2 ( p)

26. ОБРАТНАЯ СВЯЗЬ ЧЕРЕЗ ПРОМЕЖУТОЧНОЕ ЗВЕНО

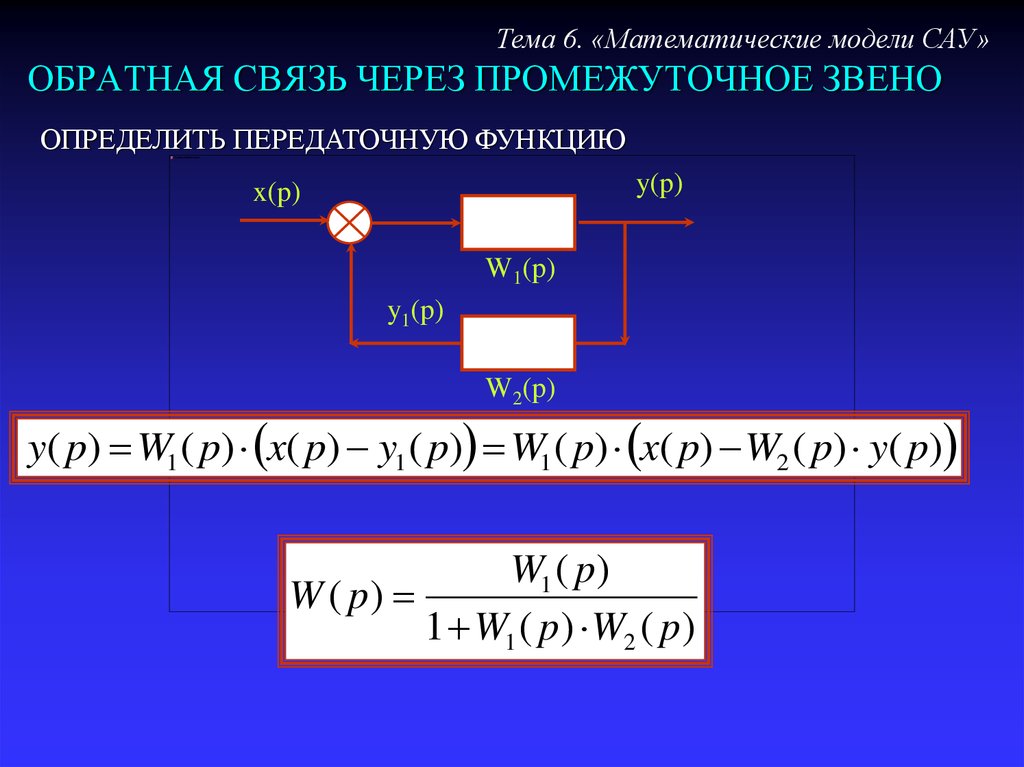
Тема 6. «Математические модели САУ»
ОБРАТНАЯ СВЯЗЬ ЧЕРЕЗ ПРОМЕЖУТОЧНОЕ ЗВЕНО
ОПРЕДЕЛИТЬ ПЕРЕДАТОЧНУЮ ФУНКЦИЮ
y(p)
x(p)
W1(p)
y1(p)
W2(p)
y( p) W1 ( p) x( p) y1 ( p) W1 ( p) x( p) W2 ( p) y( p)
W1 ( p)
W ( p)
1 W1 ( p ) W2 ( p)

27. ТЕХНОЛОГИЯ ПОЛУЧЕНИЯ МАТЕМАТИЧЕСКОЙ МОДЕЛИ АВТОМАТИЧЕСКОЙ СИСТЕМЫ УПРАВЛЕНИЯ

Тема 6. «Математические модели САУ»
ТЕХНОЛОГИЯ ПОЛУЧЕНИЯ МАТЕМАТИЧЕСКОЙ
МОДЕЛИ АВТОМАТИЧЕСКОЙ СИСТЕМЫ
УПРАВЛЕНИЯ
Для получения математической модели автоматической
системы управления необходимо:
1
все реальные элементы в системе заменить типовыми
динамическими звеньями,
2
преобразовать функциональную блок-схему в
структурную схему системы, которая представляет собой
соединение типовых динамических звеньев.
3
получить передаточную функцию системы и,
4
получить характеристическое уравнение системы или
ее математическую модель, приравняв знаменатель W(p) к 0,.

28. ПРИМЕР ПОЛУЧЕНИЯ МАТЕМАТИЧЕСКОЙ МОДЕЛИ АВТОМАТИЧЕСКОЙ СИСТЕМЫ

Тема 6. «Математические модели САУ»
ПРИМЕР ПОЛУЧЕНИЯ МАТЕМАТИЧЕСКОЙ МОДЕЛИ
АВТОМАТИЧЕСКОЙ СИСТЕМЫ
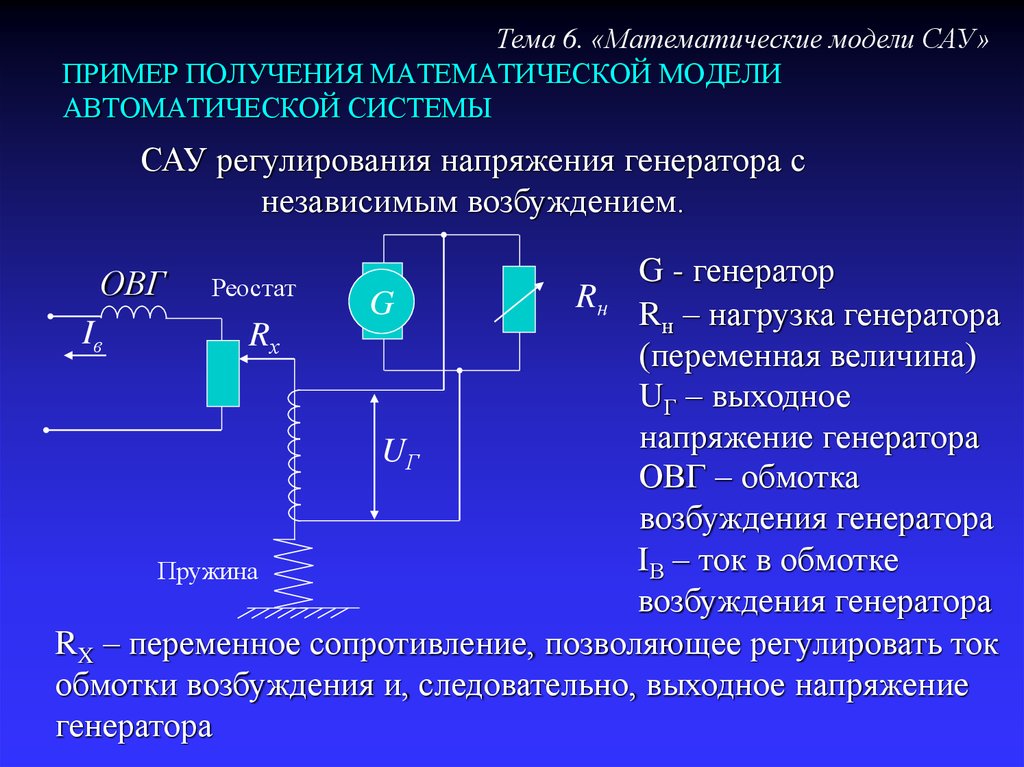
САУ регулирования напряжения генератора с
независимым возбуждением.
G - генератор
Rн
G
Rн – нагрузка генератора
Iв
Rх
(переменная величина)
UГ – выходное
напряжение генератора
UГ
ОВГ – обмотка
возбуждения генератора
IВ – ток в обмотке
Пружина
возбуждения генератора
RX – переменное сопротивление, позволяющее регулировать ток
обмотки возбуждения и, следовательно, выходное напряжение
генератора
ОВГ
Реостат

29. СОСТАВЛЯЕМ БЛОК-СХЕМУ САУ генератора

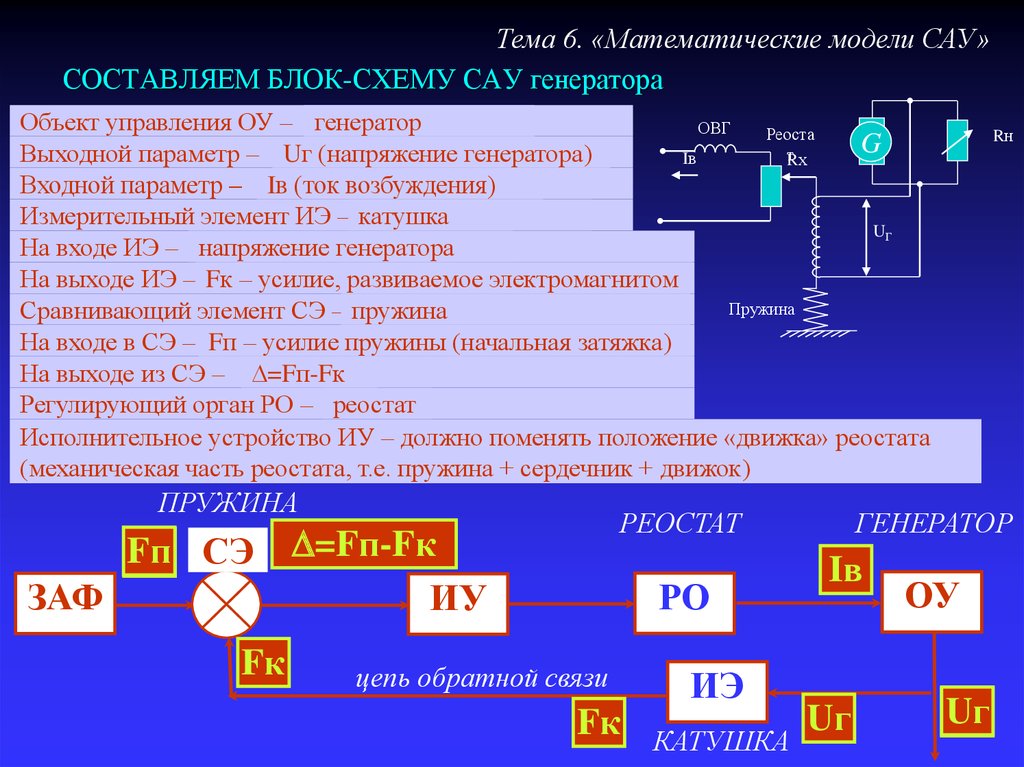
Тема 6. «Математические модели САУ»
СОСТАВЛЯЕМ БЛОК-СХЕМУ САУ генератора
Объект управления ОУ – генератор
ОВГ
Реоста
G
тRх
Выходной параметр – Uг (напряжение генератора)
Iв
Входной параметр – Iв (ток возбуждения)
Измерительный элемент ИЭ – катушка
UГ
На входе ИЭ – напряжение генератора
На выходе ИЭ – Fк – усилие, развиваемое электромагнитом
Пружина
Сравнивающий элемент СЭ – пружина
На входе в СЭ – Fп – усилие пружины (начальная затяжка)
На выходе из СЭ – D=Fп-Fк
Регулирующий орган РО – реостат
Исполнительное устройство ИУ – должно поменять положение «движка» реостата
(механическая часть реостата, т.е. пружина + сердечник + движок)
ПРУЖИНА
Fп
Х СЭ
ЗАФ
Fк
РЕОСТАТ
D=Fп-Fк
ИУ
РО
цепь обратной связи
Fк
ИЭ
КАТУШКА
Rн
ГЕНЕРАТОР
Iв
Uг
ОУ
Uг
У

30. ЗАМЕНЯЕМ ЭЛЕМЕНТЫ АВТОМАТИКИ ТИПОВЫМИ ДИНАМИЧЕСКИМИ ЗВЕНЬЯМИ

Тема 6. «Математические модели САУ»
ЗАМЕНЯЕМ ЭЛЕМЕНТЫ АВТОМАТИКИ ТИПОВЫМИ
ДИНАМИЧЕСКИМИ ЗВЕНЬЯМИ ПРУЖИНА
ГЕНЕРАТОР
Fп
Х
СЭ
D=Fп-Fк
ЗАФ
РО
ИУ
Объект управления ОУ:
Fк
цепь обратной связи
Fк
Генератор – инерционное звено
dU Г
TГ
U Г k1 I В
dt
ПЕРЕДАТОЧНАЯ ФУНКЦИЯ
ТГ
LВ
RВ
k1
k1
W1 ( p )
TГ p 1
Измерительный элемент ИЭ:
Катушка – безынерционное звено (с некоторым допущением)
FК k2U Г
ПЕРЕДАТОЧНАЯ ФУНКЦИЯ
W2 ( p) k2
Iв
ИЭ
КАТУШКА
UГ
IВ
Uг
ОУ
У
Uг

31. ПРОДОЛЖЕНИЕ

Тема 6. «Математические модели САУ»
ПРУЖИНА
ПРОДОЛЖЕНИЕ
Х
Fп
СЭ
ГЕНЕРАТОР
D=Fп-Fк
ЗАФ
Fк
цепь обратной связи
ИЭ
Fк
Исполнительное устройство ИУ:
механическая часть реостата, т.е. пружина + сердечник + движок
DF
2
m
d
d
2
m
Т
m
c DF Т
dt
2
dt
c
c
ПЕРЕДАТОЧНАЯ ФУНКЦИЯ
W 31 ( p)
k3
T22 p 2 T1 p 1
Рабочий орган РО:
Реостат – безынерционное звено (с некоторым допущением)
I В k4
ПЕРЕДАТОЧНАЯ ФУНКЦИЯ
W4 ( p) k4
Iв
РО
ИУ
1
КАТУШКА
c
Uг
ОУ
У
Uг
1
k3
с

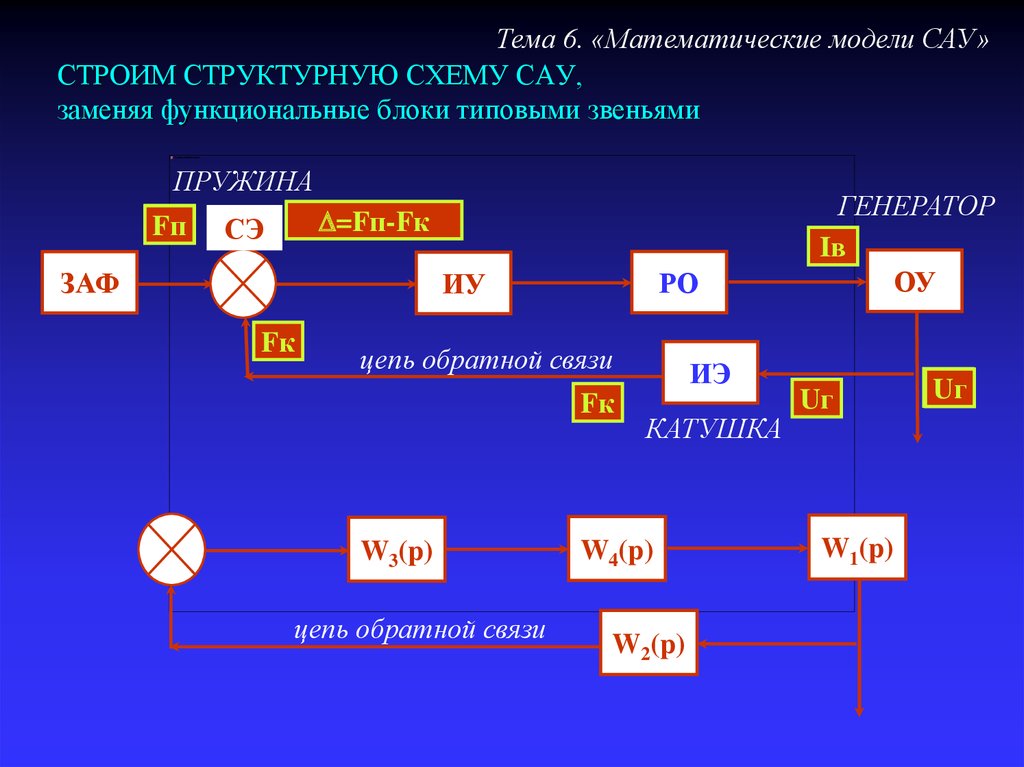
32. СТРОИМ СТРУКТУРНУЮ СХЕМУ САУ, заменяя функциональные блоки типовыми звеньями

Тема 6. «Математические модели САУ»
СТРОИМ СТРУКТУРНУЮ СХЕМУ САУ,
заменяя функциональные блоки типовыми звеньями
ПРУЖИНА
Х
Fп
D=Fп-Fк
СЭ
ЗАФ
РО
ИУ
Fк
цепь обратной связи
Fк
W3(p)
цепь обратной связи
ИЭ
КАТУШКА
W4(p)
W2(p)
ГЕНЕРАТОР
Iв
ОУ
Uг
W1(p)
У
Uг

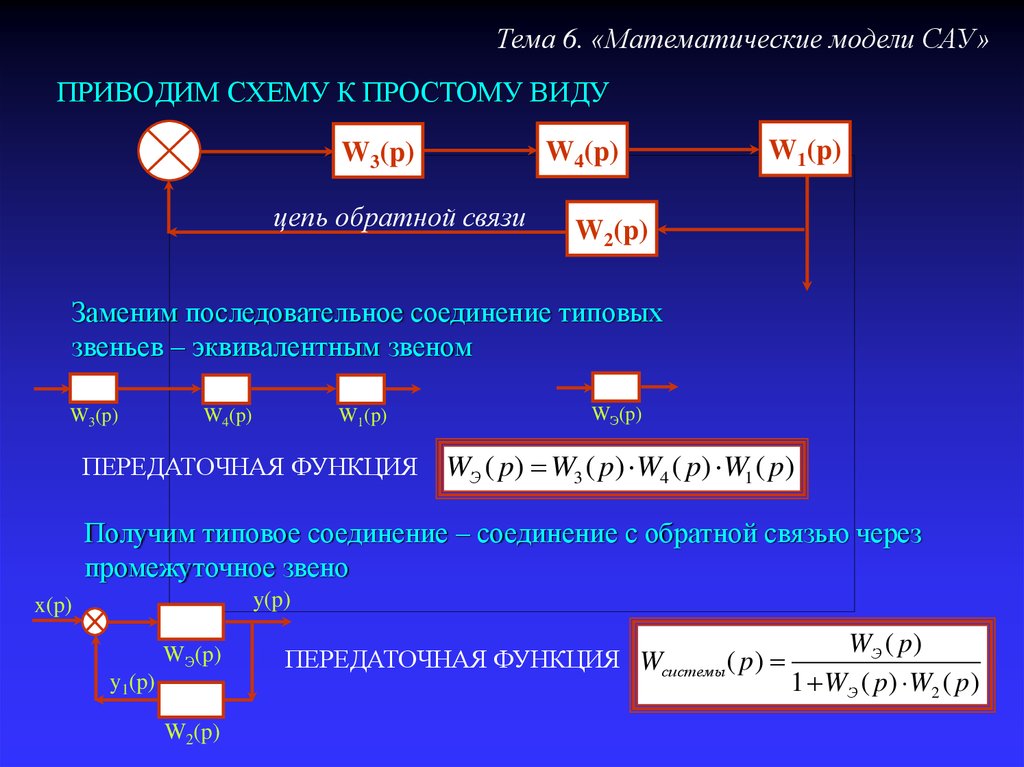
33. ПРИВОДИМ СХЕМУ К ПРОСТОМУ ВИДУ

Тема 6. «Математические модели САУ»
ПРИВОДИМ СХЕМУ К ПРОСТОМУ ВИДУ
W4(p)
W3(p)
цепь обратной связи
W1(p)
W2(p)
Заменим последовательное соединение типовых
звеньев – эквивалентным звеном
W3(p)
W4(p)
W1(p)
ПЕРЕДАТОЧНАЯ ФУНКЦИЯ
WЭ(p)
WЭ ( p) W3 ( p) W4 ( p) W1 ( p)
Получим типовое соединение – соединение с обратной связью через
промежуточное звено
y(p)
x(p)
WЭ(p)
y1(p)
W2(p)
ПЕРЕДАТОЧНАЯ ФУНКЦИЯ Wсистем ы( p)
WЭ ( p)
1 WЭ ( p) W2 ( p)

34. ПОЛУЧАЕМ МАТЕМАТИЧЕСКУЮ МОДЕЛЬ САУ

Тема 6. «Математические модели САУ»
ПОЛУЧАЕМ МАТЕМАТИЧЕСКУЮ МОДЕЛЬ САУ ОВГ
Реоста
Rн
G
тRх
Iв
ИМЕЕМ ПЕРЕДАТОЧНУЮ ФУНКЦИЮ САУ
W3 ( p) W4 ( p) W1 ( p)
Wсистем ы( p)
1 W3 ( p) W4 ( p) W1 ( p) W2 ( p)
UГ
Пружина
ПРИРАВНИВАЕМ ЗНАМЕНАТЕЛЬ К 0
1 W3 ( p) W4 ( p) W1 ( p) W2 ( p) 0
k1 k 2 k3 k 4
1
0
2 2
(TГ р 1)(Т 2 р Т1 р 1)
ПОЛУЧАЕМ ХАРАКТЕРИСТИЧЕСКОЕ
УРАВНЕНИЕ СИСТЕМЫ АВТОМАТИЧЕСКОГО
РЕГУЛИРОВАНИЯ НАПРЯЖЕНИЯ ГЕНЕРАТОРА
– МАТЕМАТИЧЕСКУЮ МОДЕЛЬ САУ
а0 р а1 р а2 р а3 0
3
а0 Т Г Т 22
а1 Т Г Т1 Т 22
2
а2 Т Г Т1
а3 1 k1 k2 k3 k4

35. ПРИМЕНЕНИЕ МАТЕМАТИЧЕСКОЙ МОДЕЛИ

Тема 6. «Математические модели САУ»
ПРИМЕНЕНИЕ МАТЕМАТИЧЕСКОЙ МОДЕЛИ
МАТЕМАТИЧЕСКУЮ МОДЕЛЬ СИСТЕМЫ
УПРАВЛЕНИЯ ПРМИЕНЯЮТ ПРИ ОЦЕНКЕ
УСТОЙЧИВОСТИ РАБОТЫ МАШИНЫ С СИСТЕМОЙ
АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ ЗАМКНУТОГО
ТИПА (НАПРИМЕР СИСТЕМЫ РЕГУЛИРОВАНИЯ
НАПРЯЖЕНИЯ ГЕНЕРАТОРА).

36. Тема 6.1 УСТОЙЧИВОСТЬ АВТОМАТИЧЕСКИХ СИСТЕМ

Тема 6. «Математические модели САУ»
Тема 6.1
УСТОЙЧИВОСТЬ
АВТОМАТИЧЕСКИХ СИСТЕМ

37. Устойчивость –

Тема 6. «Математические модели САУ»
Устойчивость –
свойство возвращаться в состояние устойчивого равновесия после
снятия возмущения, нарушевшего равновесное состояние.
Устойчивая в большом система –
имеет устойчивость при любых отклонениях управляемой
величины
Устойчивая в малом система –
обладает устойчивостью при небольших или строго
определенных отклонениях
Устойчивость – необходимое свойство
функционирования любой системы
МЕТОДЫ ОЦЕНКИ УСТОЙЧИВОСТИ
1.
2.
3.
МЕТОД ДИНАМИЧЕСКИХ (ПЕРЕХОДНЫХ) ХАРАКТЕРИСТИК
МЕТОД КОРНЕЙ ХАРАКТЕРИСТИЧЕСКИХ УРАВНЕНИЙ
СПЕЦИАЛЬНЫЕ КРИТЕРИИ УСТОЙЧИВОСТИ

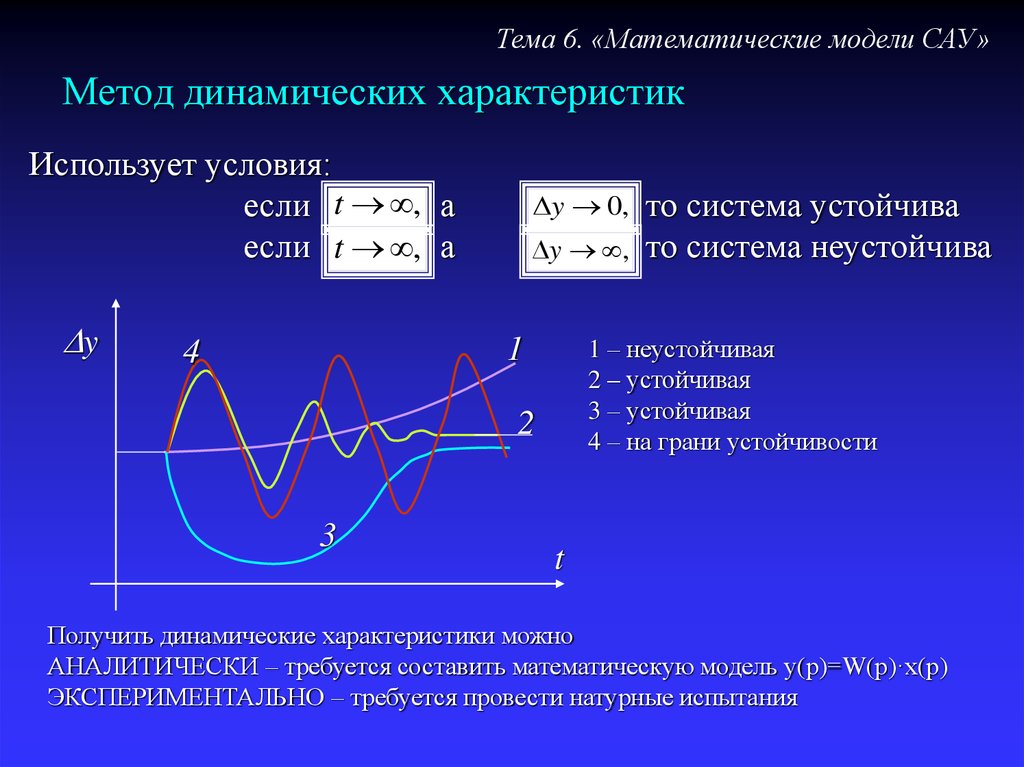
38. Метод динамических характеристик

Тема 6. «Математические модели САУ»
Метод динамических характеристик
Использует условия:
если t , а
если t , а
Dy
то система устойчива
Dy , то система неустойчива
Dy 0,
1 – неустойчивая
2 – устойчивая
3 – устойчивая
4 – на грани устойчивости
1
4
2
3
t
Получить динамические характеристики можно
АНАЛИТИЧЕСКИ – требуется составить математическую модель у(р)=W(р)·х(р)
ЭКСПЕРИМЕНТАЛЬНО – требуется провести натурные испытания

39. Метод корней характеристического уравнения

Тема 6. «Математические модели САУ»
Метод корней характеристического уравнения
ИСПОЛЬЗУЮТ ХАРАКТЕРИСТИЧЕСКОЕ УРАВНЕНИЕ – МАТЕМАТИЧЕСКУЮ
МОДЕЛЬ САУ
ПУСТЬ
ПУСТЬ
а0 р 2 а1 р а2 0
имеем
а0=1, а1=2, а2=0,5
ДЛЯ ПОЛУЧЕНИЯ КОРНЕЙ РЕШАЕМ УРАВНЕНИЕ:
a1 a12 4a0 a2
p
2a0
Корни уравнения: р1= –0,3 р2= –1,7
Для оценки устойчивости по корням уравнения используют теоремы
устойчивости Ляпунова:
Теорема 1.
ЕСЛИ ВЕЩЕСТВЕННЫЕ ЧАСТИ НЕКОТОРЫХ КОРНЕЙ
ХАРАКТЕРИСТИЧЕСКОГО УРАНЕНИЯ МЕНЬШЕ 0 , ТО СИСТЕМА –
УСТОЙЧИВА (необходимое и достаточное условие)
Теорема 2.
ЕСЛИ ВЕЩЕСТВЕННАЯ ЧАСТЬ ХОТЯ БЫ ОДНОГО ИЗ
КОРНЕЙ УРАНЕНИЯ БОЛЬШЕ 0, ТО СИСТЕМА – НЕУСТОЙЧИВА.
Теорема 3.
ЕСЛИ ВЕЩЕСТВЕННАЯ ЧАСТЬ ХОТЯ БЫ ОДНОГО ИЗ КОРНЕЙ
УРАНЕНИЯ РАВНА 0, ТО СИСТЕМА – НА ГРАНИ УСТОЙЧИВОСТИ.

40. Специальные критерии устойчивости систем

Тема 6. «Математические модели САУ»
Специальные критерии устойчивости систем
Алгебраические критерии:
критерий Гурвица,
критерий Раусса
Частотный критерий:
критерий Михайлова

41. Критерий Гурвица

Тема 6. «Математические модели САУ»
ПУСТЬ система имеет уравнение: а0 р 3 а1 р 2 а2 p a3 0
ИЗ КОЭФФИЦИЕНТОВ УРАВНЕНИЯ ФОРМИРУЕМ ДИАГОНАЛЬНЫЙ МИНОР
заполним диагональ минора коэффициентами уравнения, начиная с a1
сверху от главной диагонали размещаем коэффициенты уравнения по мере
увеличения индексов, если коэффициента нет, то ставим 0
снизу от главной диагонали размещаем коэффициенты уравнения по мере
уменьшения индексов, если коэффициента нет, то ставим 0
а1 а3 0
а а
0
0 2
0 а1 а3
ЗНАЧЕНИЕ МИНОРА D3=а3(а1а2-а3а0)
ИЗ МИНОРА ВЫСШЕГО ПОРЯДКА ФОРМИРУЕМ ОСТАЛЬНЫЕ МИНОРЫ
а1 а3
а а
0 2
ЗНАЧЕНИЕ МИНОРА D2=а1а2-а3а0
а1
D1=а1
ДЛЯ ТОГО, ЧТОБЫ СЧИТАТЬ СИСТЕМУ УСТОЙЧИВОЙ НЕОБХОДИМО И
ДОСТАТОЧНО, ЧТОБЫ ВСЕ ДИАГОНАЛЬНЫЕ МИНОРЫ БЫЛИ БОЛЬШЕ 0

42. Критерий Раусса

Тема 6. «Математические модели САУ»
ПУСТЬ система имеет уравнение: а0 р 3 а1 р 2 а2 p a3 0
СОСТАВИМ СПЕЦИАЛЬНУЮ ТАБЛИЦУ
первая строка заполняется коэффициентами с четными индексами
вторая строка заполняется коэффициентами с нечетными индексами
остальные строки заполняют коэффициентами, вычисляемыми по формуле:
ckn bk 1,n 2 rn bk 1,n 1 ,
b
rn
– коэффициенты в двух предшествующих строках,
– расчетный параметр
заполняем таблицу, пока в 1 столбце не останется свободный коэффициент, а все
остальные коэффициенты в строке должны быть равны 0
№ строки
номер столбца, k
rn
n
1
2
3
а2
а0
1
0
а3
а1
0
2
r3 = а0 а2 c13= а2 - r3 а3 c23= 0 - r3 0 c33= 0 - r3 0
3
0
0
r4 = а1 а3 c14= а3 - r4c23
4
ЧТОБЫ СИСТЕМА БЫЛА УСТОЙЧИВОЙ НЕОБХОДИМО И ДОСТАТОЧНО, ЧТОБЫ
ВСЕ КОЭФФИЦИЕНТЫ ПЕРВОГО СТОЛБЦА БЫЛИ БОЛЬШЕ 0

43. Критерий Михайлова

Тема 6. «Математические модели САУ»
Критерий Михайлова
ПУСТЬ система имеет уравнение: а0 р 3 а1 р 2 а2 p a3 0
Запишем уравнение в форме полинома через оператор Лапласса
D( p) а0 р 3 а1 р 2 а2 p a3
Заменим оператор р комплексной переменной jw
D( jw ) а0 ( jw )3 а1 ( jw ) 2 а2 ( jw ) a3
Представим вектор D( jw) в виде
D( jw ) B(w ) jM (w )
В(w)
jM(w)
– действительная часть вектора,
– мнимая часть вектора
B(w ) a3 a1 ( jw ) 2 a3 a1w 2
четные степени дают
нечетные степени дают
jM (w ) a0 ( jw )3 a2 ( jw ) jw (a2 a0w 2 )
ДЛЯ ОЦЕНКИ УСТОЙЧИВОСТИ СИСТЕМЫ НЕОБХОДИМО НАЙТИ ТОЧКИ
ПЕРЕСЕЧЕНИЯ ВЕКТОРА D( jw) С ОСЯМИ КОМПЛЕКСНОЙ ПЛОСКОСТИ

44. Точки пересечения с осями комплексной плоскости

Тема 6. «Математические модели САУ»
Точки пересечения с осями комплексной плоскости
ПУСТЬ система имеет уравнение: а0 р 3 а1 р 2 а2 p a3 0
ПУСТЬ
Пересечение с мнимой осью
B(w ) 0 :
a3 a1w 2 0
а0=1, а1=4, а2=1, а3=1
w1
a3
0,5
a1
M (w1 ) jw1 (a2 a0w12 ) 0,5(1 1 0,52 ) 0,375
Пересечение с действительной осью
M (w ) 0 :
w (a2 a0w 2 ) 0
B(w 2 ) a3 a1w 22 1 2 0 2 1
1
B(w 3 ) a3 a1w 32 1 2 1
1
w2 0
w3
a2
1
a0

45. Имеем три точки пересечения

Тема 6. «Математические модели САУ»
Имеем три точки пересечения
ОТМЕТИМ ТОЧКИ НА МНИМОЙ ПЛОСКОСТИ
Начинаем с точки имеющей наименьшее значение частоты w:
w2=0
M(w2)=0
B(w2)=1
w1=0,5 M(w1)=0,375
B(w1)=0
w3=1
M(w3)=0
B(w3)=-1
СТРОИМ ВЕКТОР D(jw)
ЧТОБЫ СИСТЕМА БЫЛА УСТОЙЧИВОЙ
НЕОБХОДИМО И ДИСТАТОЧНО,
M(
w
)
n=1
n=3
ЧТОБЫ ВЕКТОР D(jw) НАЧАЛ СВОЕ
D1(jw)
ДВИЖЕНИЕ С ПОЛОЖИТЕЛЬНОЙ
ЧАСТИ ДЕЙСТВИТЕЛЬНОЙ ОСИ И
ПРИ ИЗМЕНЕНИИ w ОТ 0 ДО ∞
№2
D2(jw)
+0,375
ПОСЛЕДОВАТЕЛЬНО ПРОШЕЛ
B(w) n КВАДРАТОВ ПЛОСКОСТИ,
№1
№3
ПОВЕРНУВШИСЬ ПРОТИВ ЧАСОВОЙ
0
-1
+1
СТРЕЛКИ НА УГОЛ n=p/2 И НИГДЕ
D(jw)
D3(jw)
НЕ ОБРАТИЛЯ В 0
n=4
ВЫВОД:
n=2
СИСТЕМА, ИМЕЮЩАЯ ВЕКТОР D(jw) - УСТОЙЧИВА
СИСТЕМА, ИМЕЮЩАЯ ВЕКТОР D1(jw) - НЕУСТОЙЧИВА
СИСТЕМА, ИМЕЮЩАЯ ВЕКТОР D2(jw) - УСТОЙЧИВА
СИСТЕМА, ИМЕЮЩАЯ ВЕКТОР D3(jw) - НЕУСТОЙЧИВА