Понятие управления

1.

Часть 1.
Введение

2. Понятие управления

• Управление
—
это
процесс
планирования,
организации, мотивации и контроля, необходимый
для того, чтобы сформулировать и достичь цель.
• Управление — в теории: наука о принципах и
методах управления различными системами.
• Управление технической системой – создание
условий, обеспечивающих требуемое протекание
технологического процесса, то есть поддержание
необходимого технологического режима с точки
зрения качества получаемой продукции.

3.

4.

Современный этап развития промышленного производства
характеризуется переходом к высоким технологиям,
стремлением добиться высокой эффективности производства в
условиях массовой и жесткой конкуренции.
Высокие технологии подразумевают под собой часто
протекание технологических процессов в условиях близких к
критическим , отклонения от которых могут привести к
аварийным ситуациям и тяжелым последствиям. То есть,
современное производство является сложным и
потенциально опасным.
В связи с этим повышаются требования к точности и
эффективности проведения процесса - то есть к управлению им
– возрастает роль автоматизации производства.

5.

• Автоматизация – комплекс технических, методических,
организационных и других мероприятий, позволяющих вести
управление тем или иным объектом автоматически, то есть без
непосредственного участия человека.

6.

Процесс развития автоматизации прошел ряд стадий, связанных
с соответствующим уровнем развития техники и производства.
Первым этапом автоматизации явилось ручное управление.
Человек первоначально решал сам все задачи и приводил в
исполнение свои решения. Вручную открывал/закрывал задвижки
изменяя потоки/количества вещества или энергии, оценивал состояние
процессов/аппаратов «на глаз».
Человек и принимает решения и приводит их в исполнение

7.

Вторым этапом в развитии автоматизации стала механизация.
Производство усложнялось, требовалось более точное и быстрое
управление , появились приборы для определения состояния вещества
(температуры, давления, массы, скорости и пр.). Рутинные действия
(открытие/закрытие задвижек, кранов, перемешивание продуктов и пр.)
стали осуществляться с помощью механических устройств.
В механизированном производстве
человек принимает непосредственное участие
в процессе управления, но освобожден от
тяжелого физического труда.
труда. Основная
Основная его
его
задача – принятие решений.
Механизация облегчает
облегчает труд,
труд, уменьшает
уменьшает
численность персонала, увеличивает
производительность труда.
труда.

8.

С дальнейшим усложнением производства (высокие
температуры, скорости реакций и пр.) человек уже не в состоянии
своевременно принимать верные решения. Часть функций управления
стала возлагаться на автоматические устройства (регуляторы),
которые без непосредственного участия человека не просто открывали
и закрывали задвижки, клапаны, заслонки и пр., но и высчитывали
степень закрытия и открытия.
Современный этап развития автоматизации характеризуется
широким применением вычислительной техники для управления
производством. Однако, любая система управления предполагает
участие человека в процессе управления.

9. 1.1. Системы управления. Системы управления предприятием. Автоматизированные системы управления технологическими процессами.

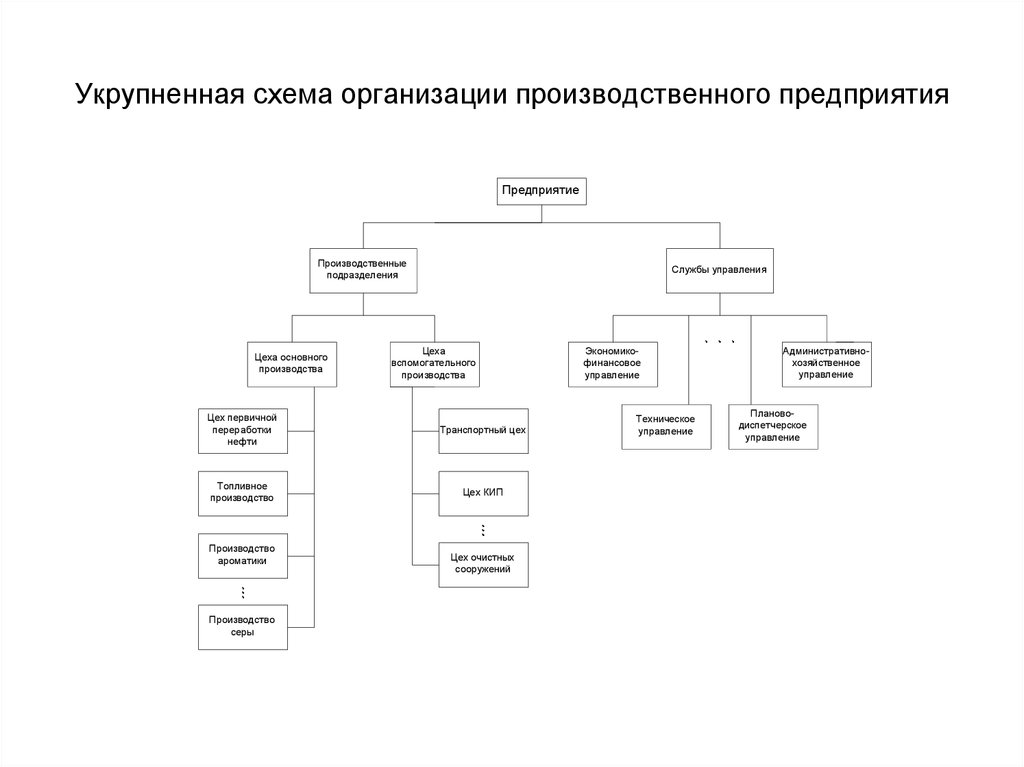
10. Укрупненная схема организации производственного предприятия

Предприятие
Производственные
подразделения
Цеха основного
производства
Службы управления
Цеха
вспомогательного
производства
Цех первичной
переработки
нефти
Транспортный цех
Топливное
производство
Цех КИП
Производство
ароматики
Производство
серы
Цех очистных
сооружений
Экономикофинансовое
управление
Техническое
управление
Административнохозяйственное
управление
Плановодиспетчерское
управление

11. Иерархическая структура системы управления предприятием

АСУП
автоматизированная система
управления предприятием
АСУПП
автоматизированная
система управлением
производственным
подразделением
АСУТП
автоматизированная
система управления
технологическим
процессом
АСУТП
автоматизированная
система управления
технологическим
процессом
САР (АСР)
САР (АСР)
САР (АСР)
системы
автоматического
регулирования
системы
автоматического
регулирования
системы
автоматического
регулирования
АСУПП
автоматизированная
система управлением
производственным
подразделением
АСУТП
автоматизированная
система управления
технологическим
процессом
АСУПП
автоматизированная
система управлением
производственным
подразделением
АСУПП
автоматизированная
система управлением
производственным
подразделением

12.

Технологический процесс – совокупность технологических операций,
проводимых над исходным сырьем в одном или нескольких аппаратах с целью
получения продукта, обладающего заданными свойствами.
Технологический объект – совокупность технологического
оборудования и реализованного на нем по соответствующему регламенту
технологического процесса производства. Технологический объект является
составной частью технологического процесса.
Задача управления технологическим процессом состоит в выработке
оптимальных режимных параметров технологических аппаратов и
оборудования для обеспечение желаемого протекания процесса, качества и
количества продукции.
Задача управления технологическим объектом – поддержание
заданных режимных параметров (давление, температура, уровень,
концентрация и пр.).

13. 1.2. Основные функции АСУ ТП

Основные функции АСУ ТП
информационно-измерительная
управляющая
вспомогательная

14.

информационно-измерительная:
-измерение, отображение и регистрация технологических параметров и
состояния оборудования;
-косвенные измерения;
-обнаружение отклонений;
-регистрация и анализ аварийных ситуаций;
-прогноз протекания технологического процесса.
управляющая:
-поддержание заданных технологических параметров в условиях
действующих возмущений;
-изменение параметров по определенному закону;
-распределение нагрузки между аппаратами;
-управление в режимах пуска-останова;
-управление в нестандартных условиях (аварийная защита и блокировка).
вспомогательная:
-архивирование событий;
-обмен информацией с системами высших уровней иерархии.

15. Программно-техническое обеспечение АСУ ТП

-технические средства и обеспечение (датчики, преобразователи,
усилители, системы передачи сигналов на расстояние, регуляторы,
контроллеры, исполнительные механизмы, клапаны, отсекатели,
задвижки, устройства ввода-вывода сигналов, компьютеры, мониторы,
принтеры и пр.).
-программное обеспечение (общесистемное и специальное
программное обеспечение).

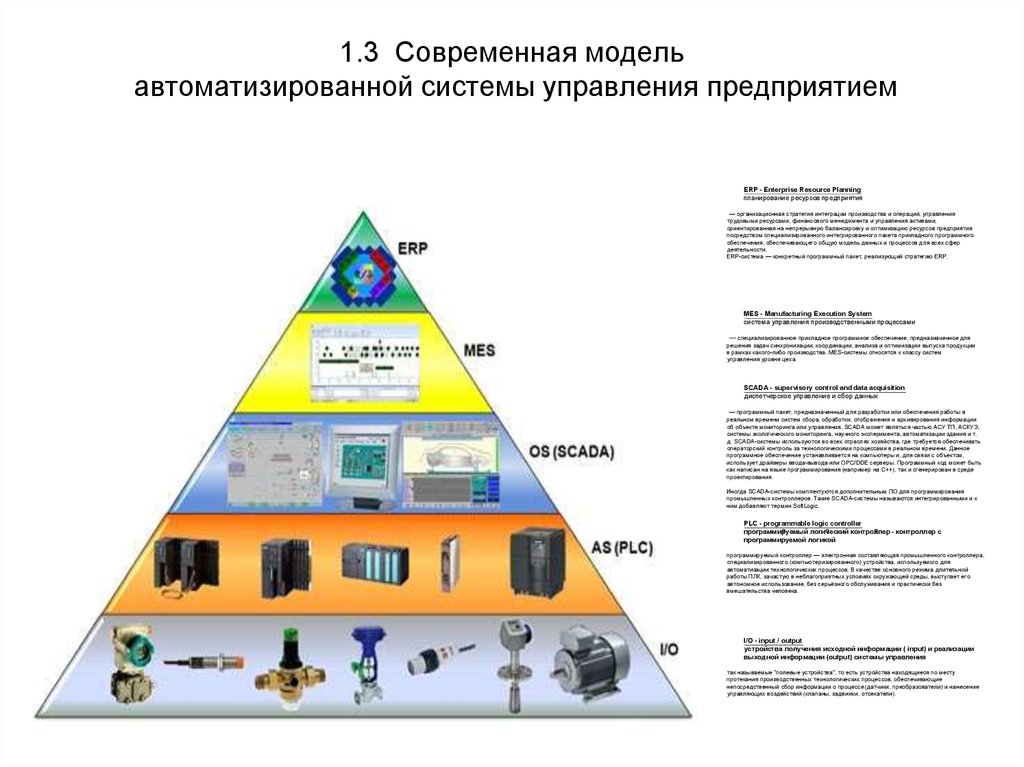
16. 1.3 Современная модель автоматизированной системы управления предприятием

ERP - Enterprise Resource Planning
планирование ресурсов предприятия
— организационная стратегия интеграции производства и операций, управления
трудовыми ресурсами, финансового менеджмента и управления активами,
ориентированная на непрерывную балансировку и оптимизацию ресурсов предприятия
посредством специализированного интегрированного пакета прикладного программного
обеспечения, обеспечивающего общую модель данных и процессов для всех сфер
деятельности.
ERP-система — конкретный программный пакет, реализующий стратегию ERP.
MES - Manufacturing Execution System
система управления производственными процессами
— специализированное прикладное программное обеспечение, предназначенное для
решения задач синхронизации, координации, анализа и оптимизации выпуска продукции
в рамках какого-либо производства. MES-системы относятся к классу систем
управления уровня цеха.
SCADA - supervisory control and data acquisition
диспетчерское управление и сбор данных
— программный пакет, предназначенный для разработки или обеспечения работы в
реальном времени систем сбора, обработки, отображения и архивирования информации
об объекте мониторинга или управления. SCADA может являться частью АСУ ТП, АСКУЭ,
системы экологического мониторинга, научного эксперимента, автоматизации здания и т.
д. SCADA-системы используются во всех отраслях хозяйства, где требуется обеспечивать
операторский контроль за технологическими процессами в реальном времени. Данное
программное обеспечение устанавливается на компьютеры и, для связи с объектом,
использует драйверы ввода-вывода или OPC/DDE серверы. Программный код может быть
как написан на языке программирования (например на C++), так и сгенерирован в среде
проектирования.
Иногда SCADA-системы комплектуются дополнительным ПО для программирования
промышленных контроллеров. Такие SCADA-системы называются интегрированными и к
ним добавляют термин SoftLogic.
PLC - programmable logic controller
программи?
руемый логи?
ческий контро?
ллер - контроллер с
программируемой логикой
программируемый контроллер — электронная составляющая промышленного контроллера,
специализированного (компьютеризированного) устройства, используемого для
автоматизации технологических процессов. В качестве основного режима длительной
работы ПЛК, зачастую в неблагоприятных условиях окружающей среды, выступает его
автономное использование, без серьёзного обслуживания и практически без
вмешательства человека.
I/O - input / output
устройства получения исходной информации ( input) и реализации
выходной информации (output) системы управления
так называемые "полевые устройства", то есть устройства находящиеся по месту
протекания производственных технологических процессов, обеспечивающие
непосредственный сбор информации о процессе (датчики, преобразователи) и нанесение
управляющих воздействий (клапаны, задвижки, отсекатели).

17. 1.4. Пример представления системы управления (регулирования) технологическим объектом.

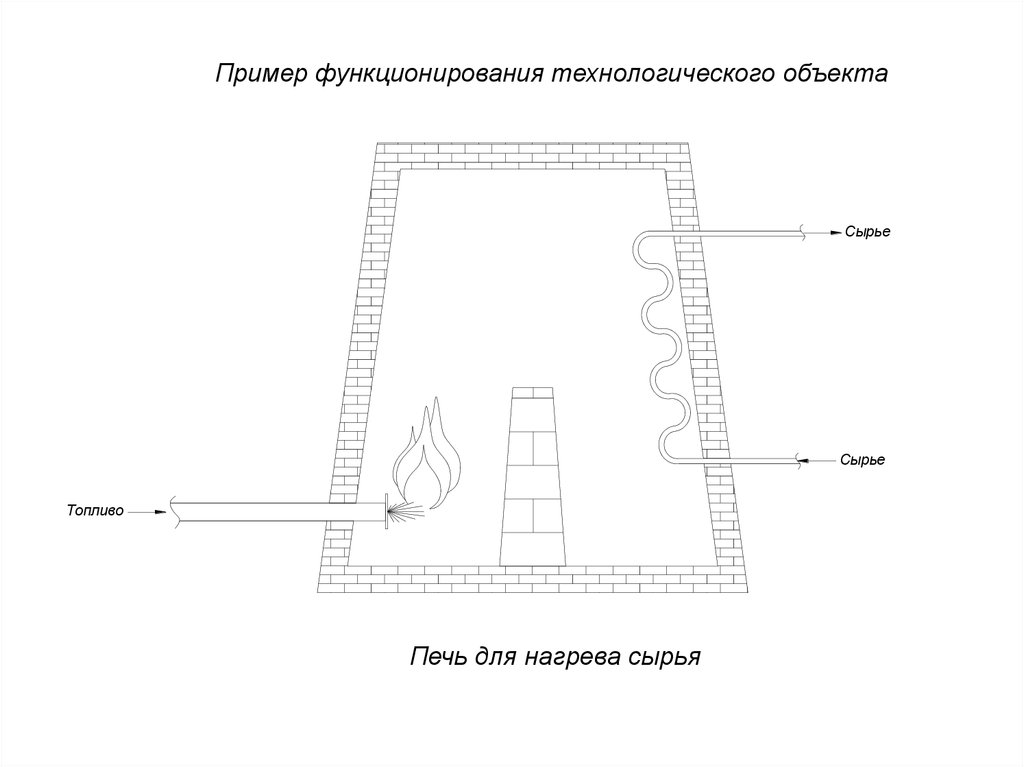
18.

Пример функционирования технологического объекта
Сырье
Сырье
Топливо
Печь для нагрева сырья

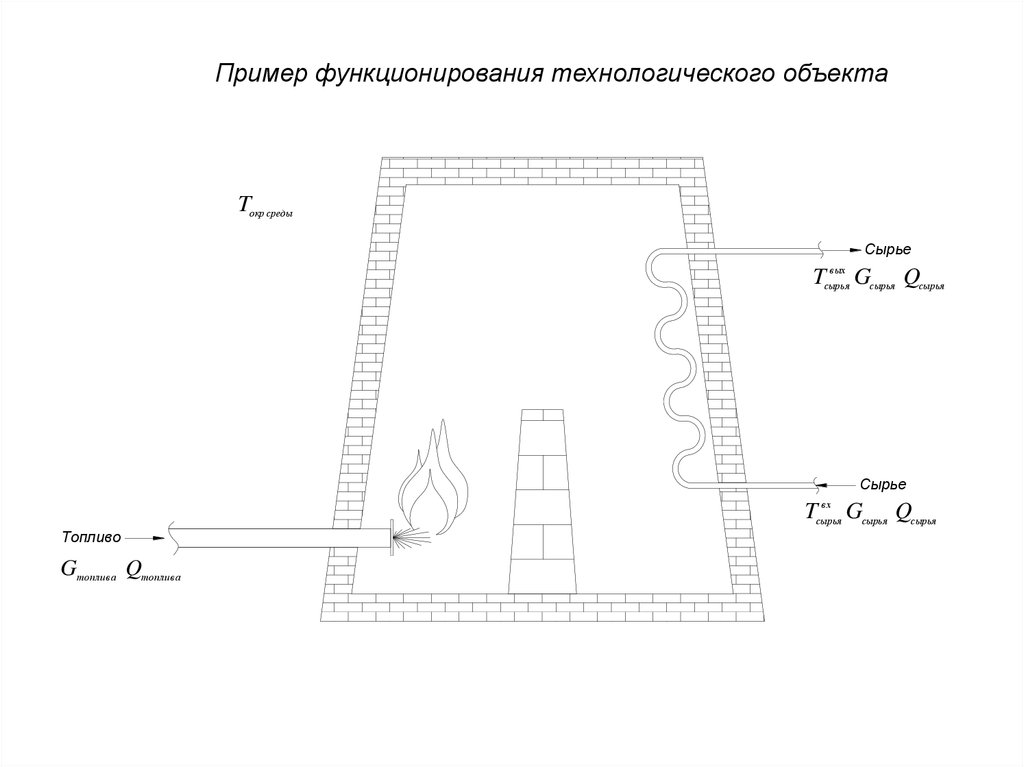
19.

Пример функционирования технологического объекта
Tокр среды
Сырье
вых
Tсырья
Gсырья Qсырья
Сырье
вх
Tсырья Gсырья Qсырья
Топливо
Gтоплив а Qтоплив а

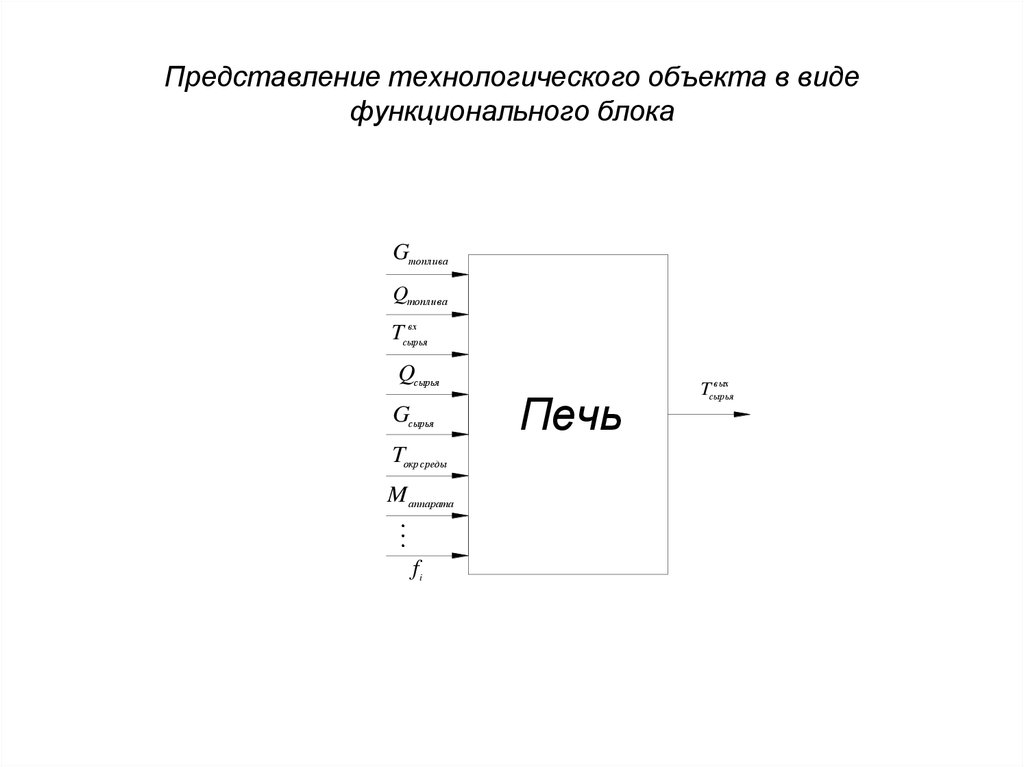
20. Представление технологического объекта в виде функционального блока

Gтоплив а
Qтоплива
вх
Tсырья
Qсырья
Gсырья
Tокр среды
M аппарата
fi
Печь
в ых
Tсырья

21. Переход от физического понятия технологического объекта к понятию «объект управления»

fi
Qтоплив а Tокр среды M аппарата
вх
Tсырья
Qсырья Gсырья
Gтоплив а
Печь
вых
Tсырья
f1
x
fi
f1
fn
Печь
y
x
fi fn
Объект
управления
y

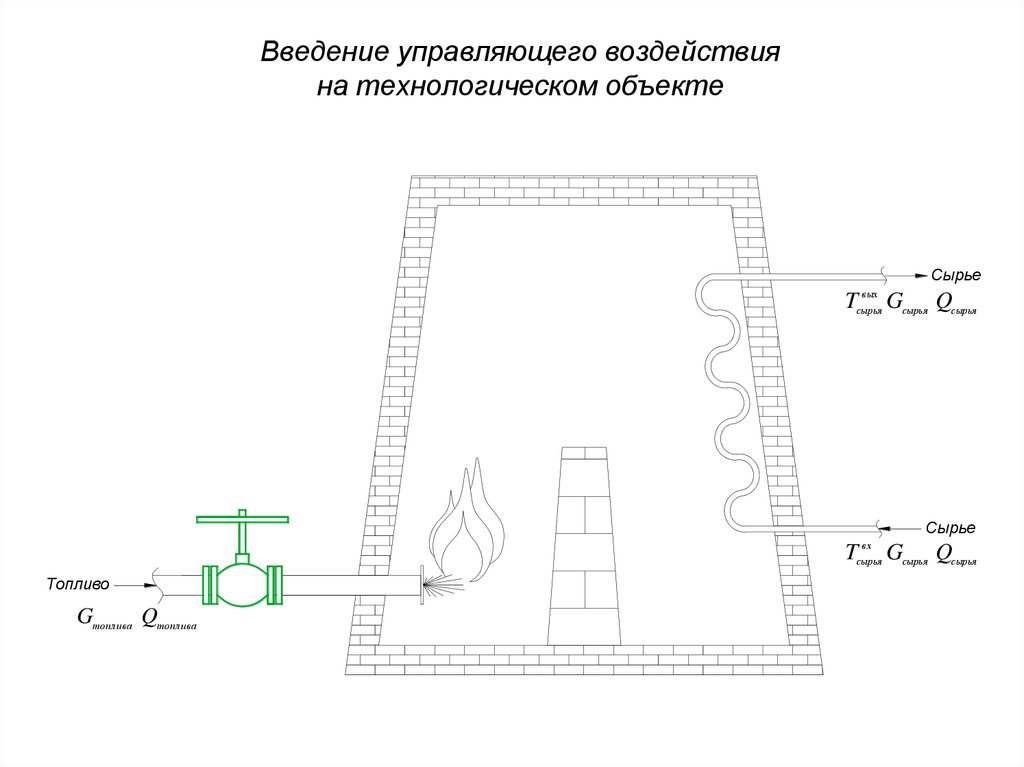
22. Введение управляющего воздействия на технологическом объекте

Сырье
вых
Tсырья Gсырья Qсырья
Сырье
вх
Tсырья Gсырья Qсырья
Топливо
Gтоплив а Qтоплив а

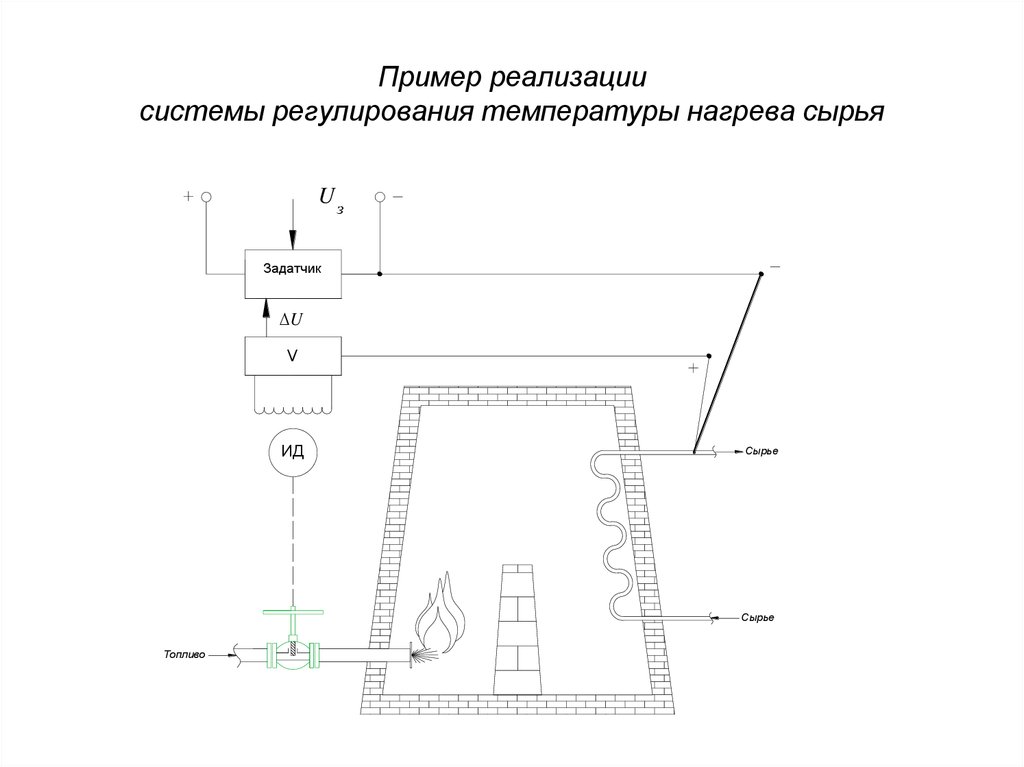
23. Пример реализации системы регулирования температуры нагрева сырья

Uз
Задатчик
U
V
ИД
Сырье
Сырье
Топливо

24. Построение функциональной схемы системы регулирования температуры нагрева сырья

fi
Qтоплив а Tокр среды M аппарата
вх
Tсырья
Qсырья Gсырья
Задатчик
в ых
Tсырья
заданная
в ых
Tсырья
Печь
Gтоплив а
в ых
Tсырья
Датчик
в ых
Tсырья
Сравнительный
элемент
Устройство
принятия
решений
Исполнительный
двигатель
РО
Gтоплив а

25. Преобразование структуры функциональной схемы регулирования

fi
Qтоплива Tокр среды M аппарата
вх
Tсырья
Qсырья
вых
Tсырья
Gсырья
в ых
Tсырья
Печь
заданная
в ых
Tсырья
в ых
Tсырья
Сравнительный
элемент
Датчик
Устройство
принятия
решений
Исполнительный
двигатель
РО
Gтоплива
Gтоплива
fi
Tокр среды M аппарата
вх
Tсырья
вых
Tсырья
заданная
Сравнительный
элемент
в ых
Tсырья
Устройство
принятия
решений
Исполнительный
двигатель
РО
Gтопл
вых
Tсырья
вых
Tсырья
Датчик
вых
Tсырья
Qсырья
Печь
Gсырья
в ых
Tсырья

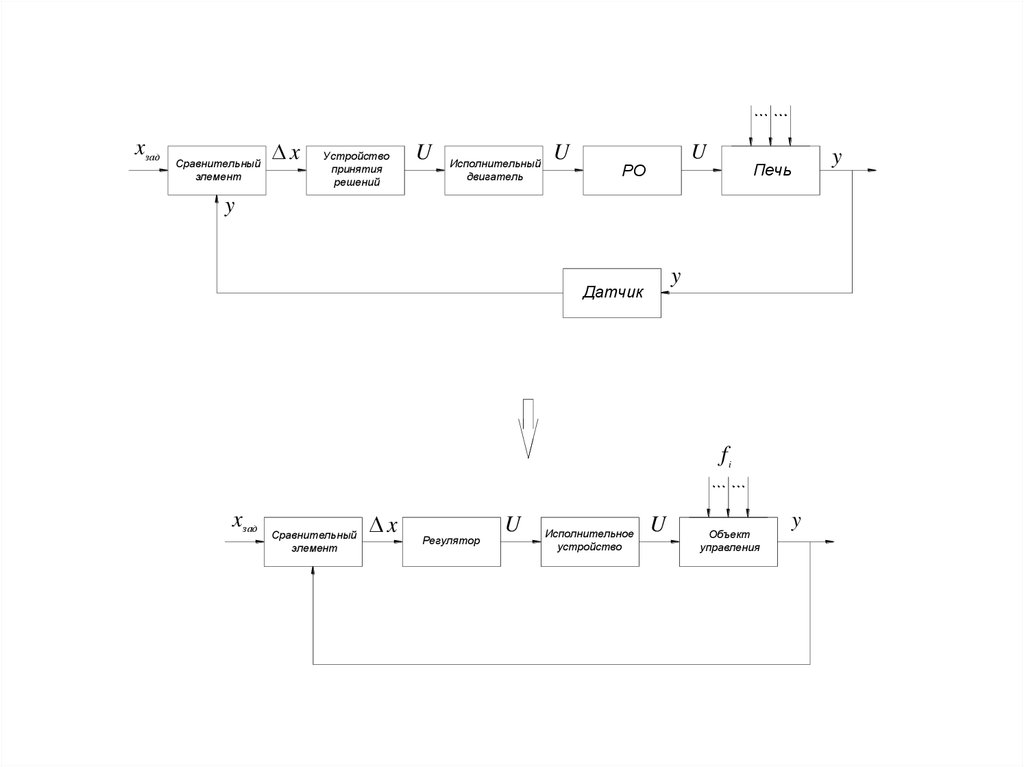
26.

xзад
Сравнительный
элемент
x
Устройство
принятия
решений
U
Исполнительный
двигатель
U
U
РО
y
Печь
y
y
Датчик
fi
xзад
Сравнительный
элемент
x
Регулятор
U
Исполнительное
устройство
U
Объект
управления
y

27.

2. Основные термины ТАУ

28. 2.1. Основные понятия и определения ТАУ

fi
x
е
U
Регулятор
Исполнительное
устройство
U
y
Объект
управления
y
Объект управления (ОУ) – любой аппарат, машина, агрегат в котором протекает
технологический процесс, подвергающийся управлению.
Регулируемая величина y t – физический параметр, характеризующий состояние объекта
управления (ОУ).
Задание (задающие воздействие) x t - желаемое значение регулируемой величины.
Ошибка регулирования e t - отклонение регулируемой величины от заданного значения.
e t x t y t
Возмущающее воздействие (возмущение) f t - внешнее воздействие стремящееся
вызвать нежелательное отклонение регулируемой величины от заданного значения.
Управляющее воздействие u t - воздействие наносимое системой регулирования на объект
с целью выведения регулируемой величины на заданное значение.
Регулятор – совокупность автоматически действующих устройств, обеспечивающих процесс
регулирования без участия человека.
Автоматическое регулирование – поддержание постоянным значения некоторой физической
величины, или изменение ее по некоторому, возможно заранее неизвестному закону, с
помощью автоматически действующих устройств.

29. 2.2.Классификация АСР.

2.2.1.Классификация по принципу регулирования
Процесс управления возможен при достаточной информации:
• - о цели управления;
• - о состоянии объекта управления;
• - о характеристиках объекта;
• - о возмущениях среды.
В зависимости от характера и полноты доступной информации реализуют
различные принципы регулирования
- принцип регулирования по отклонению;
- принцип регулирования по возмущению;
- комбинированное регулирование.

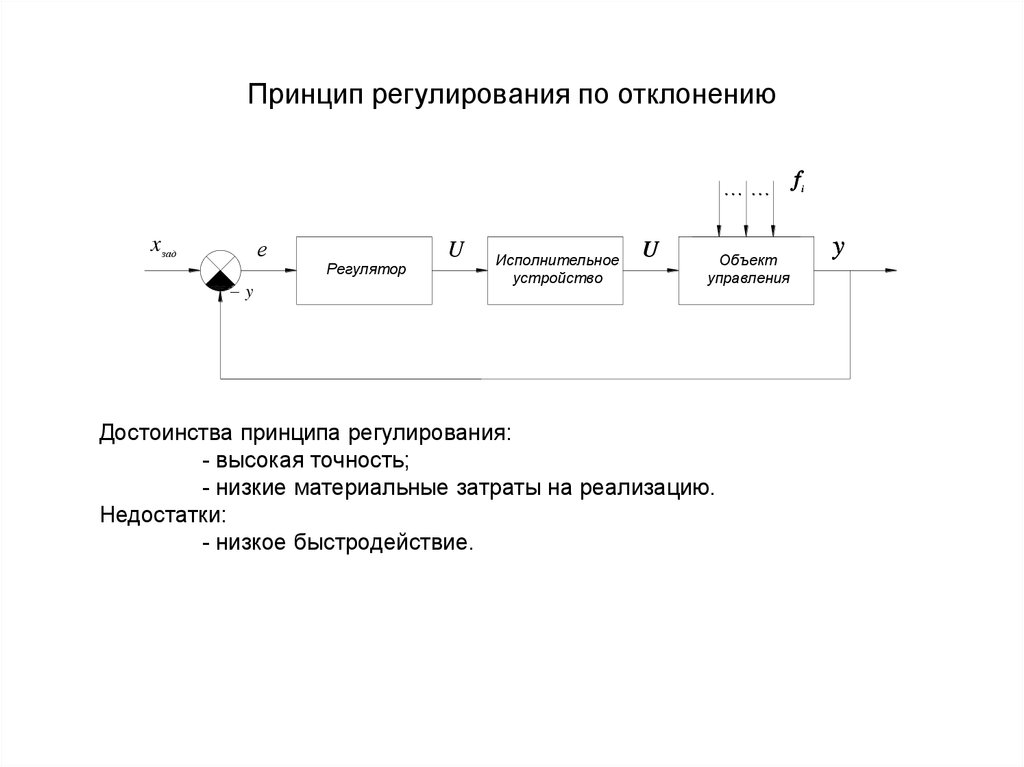
30. Принцип регулирования по отклонению

fi
xзад
е
y
Регулятор
U
Исполнительное
устройство
U
Объект
управления
Достоинства принципа регулирования:
- высокая точность;
- низкие материальные затраты на реализацию.
Недостатки:
- низкое быстродействие.
y

31.

Принцип регулирования по возмущению
f
fi
f
xзад
е
Регулятор
n
Дn
f
Дi
i
Д1
1
U
Исполнительное
устройство
U
Достоинства принципа регулирования:
- высокое быстродействие.
Недостатки:
- низкая точность;
- высокие материальные затраты на реализацию.
Объект
управления
y

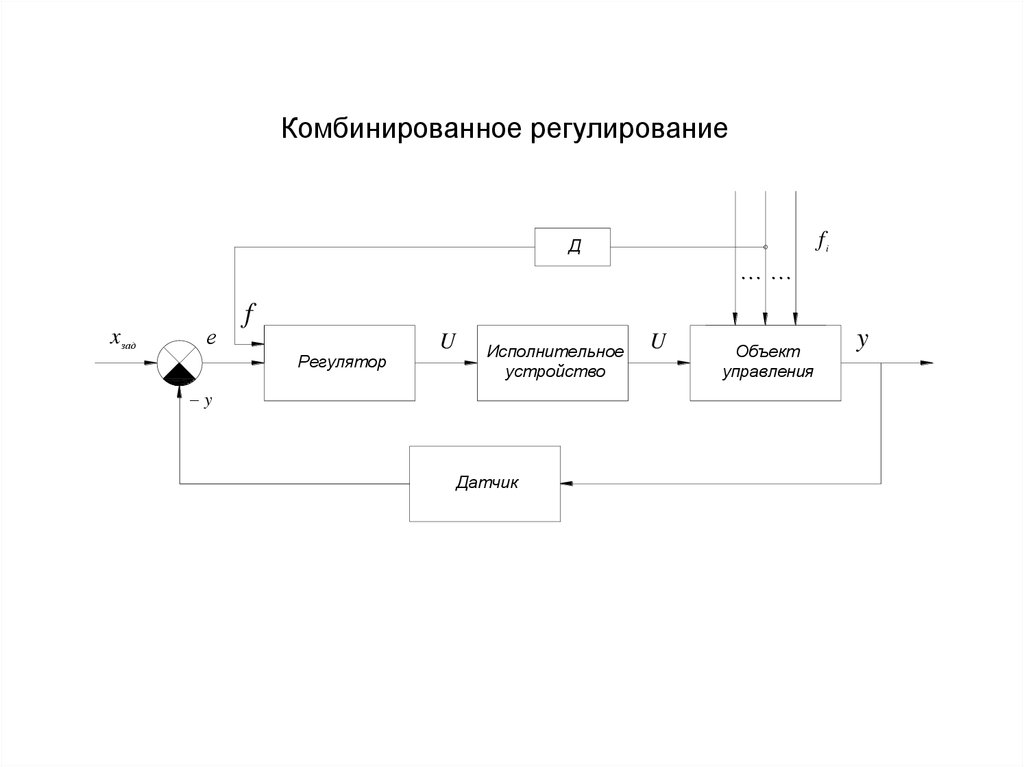
32.

Комбинированное регулирование
fi
Д
xзад
е
f
Регулятор
U
Исполнительное
устройство
y
Датчик
U
Объект
управления
y

33. 2.2.2. Классификация по виду задающего воздействия

По виду задающего воздействия х t АСР делят на:
• - системы стабилизации ;
• - системы программного управления;
• - следящие системы.
2.2.3. Классификация по типу используемых сигналов
По типу используемых сигналов АСР делят на:
• - непрерывные АСР ;
• - дискретные АСР.
2.2.4. Многосвязные и односвязные АСР
Односвязные АСР – каждой регулируемой величине соответствует свой
регулирующий орган и управляющее воздействие.
Многосвязные АСР – изменение одного управляющего воздействия приведет к
изменению нескольких регулируемых величин.

34. 2.2.5. По основным видам уравнений динамики

линейные
с постоянными
коэффициентами
с переменными
коэффициентами
нелинейные
с распределенными
параметрами
системы с
запаздыванием

35.

3.Математический аппарат ТАУ

36.

3.1. Математические модели в АСР.
В теории управления любые физические объекты и явления рассматриваются в
виде математических зависимостей между входными и выходными величинами –
математическими моделями.
Математическая модель – совокупность уравнений, позволяющих определить
(рассчитать) выходной сигнал по известному входному сигналу.
х
y
Основой для анализа и синтеза АСР является математическая модель как АСР в
целом, так и отдельных ее звеньев.
Наиболее широко употребляемой является математическая модель в виде
дифференциального уравнения
dny
d n 1 y
d n 2 y
di y
dy
d mx
d m 1 x
d m 2 x
dix
dx
an n an 1 n 1 an 2 n 2 .... ai i .... a1
a0 y bm m bm 1 m 1 bm 2 m 2 ... bi i ... b1
b0 x
dt
dt
dt
dt
dt
dt
dt
dt
dt
dt

37.

Однако эти модели подразумевают операции интегрирования и
дифференцирования, что значительно усложняет анализ и синтез систем в
смысле расчетов.
3.2. Преобразование Лапласа
В ТАУ для упрощения математических моделей применяют аппарат операционного
исчисления – преобразование Лапласа.
Операционное исчисление – совокупность методов прикладного математического
анализа, позволяющих экономно и непосредственно ведущими к цели
средствами получать решения линейных дифференциальных уравнений.
3.2.1. Прямое преобразование Лапласа
При преобразовании Лапласа функции действительного переменного f t (функцияоригинал) ставится в соответствие функция комплексного переменного
(функция-изображение).
F S
F S f t
F S L f t
f t , t 0
f t
0, t 0
F S f t e dt
f t M e
0
St
α0 t

38.

Во многих случаях при нахождении решения f t можно избежать вычисления этого
оригинала воспользовавшись таблицей оригиналов и их изображений.
3.2.2. Таблица простейших оригиналов и их изображений
f t
t
1 t
F S
1
1
S
t
1
S2
e
at
1
S a
te
at
1
(S a)2
t k 1 at
e
k 1 !
1
(S a)k
tn
n!
S n 1

39.

3.2.3. Свойства преобразования Лапласа
Теория преобразования Лапласа включает в себя ряд теорем (свойств), опираясь
на которые, можно достаточно просто переходить от оригиналов к
изображениям.
Теорема линейности.
L f 1 t f 2 t L f 1 t L f 2 t F1 S F2 S
L C f t C F S
Теорема дифференцирования
L f t S F S f 0 ,
f 0 lim f t
t 0
d n f t
d n 1 f t n 1
0
L
S L
f
n
n 1
dt
dt
при нулевых начальных условиях
L f k t S k F S

40.

Теорема интегрирования
t
F S
L f t dt
f 1 0 ,
S
0
f 1 0 начальные значения интеграла
при нулевых начальных условиях
t
1
L ... f t dt k F S
0
S
k
Теорема запаздывания (смещения)
L f t τ e- S F S
Теорема о начальных и конечных значениях
lim f t lim S F S
t 0
S
lim f t lim S F S
t
S 0

41. 3.2.4. Обратное преобразование Лапласа

Переход от изображения к оригиналу осуществляется по формуле обратного
преобразования Лапласа.
f t F S
1
f t L F S
j2π
-1
c jw
F S e
St
dS
c jw
На практике для нахождения оригинала по известному изображению часто
используют метод разложения сложной дроби на сумму простых дробей.
Пусть f t F S , и F S является рациональной функцией:
m
F S
m 1
bm S bm 1 S ... bi S ...b1 S b0
an S n an 1 S n 1 ... ai S i ...a1 S a0
m
i
b S
i
a S
i
i 0
n
i 0
i
B S
A S
m n
i
Из курса математики сложную дробь можно разложить на сумму простых дробей
bm S m bm 1S m 1 ... bi S i ...b1 S b0
Mi
Mn
M1
M2
F S
...
...
n
n 1
i
an S an 1S ... ai S ...a1 S a0
S S1 S S 2
S Si
S Sn
где
S1 , S 2 , S n корни полинома
A S 0 , M i S lim
S Si
B S S Si
B Si
,
A S
A Si
n
Mi
S S
i 1
где A S
i
d
A S S Si
dS

42.

Тогда, переходя к оригиналу
n Mi
f t L 1 F S L 1
S
S
i
i 1
n
M
i 1
i
1
L 1
S Si
Из таблицы оригиналов и изображений:
1 Si t
L 1
e
S
S
i
Можно записать
f t
n
1
S t
1
M
L
Mi e i
i
i 1
S Si i 1
n
Таким образом, можно говорить о том, что функция-оригинал может быть найдена
как сумма экспонент. При этом степень каждой экспоненты определяется
соответствующим корнем знаменателя функции-изображения (или корнем
полинома А(S) ).

43.

3.2.5.* Решение дифференциальных уравнений с помощью теории
преобразования Лапласа
С помощью преобразования Лапласа существенно облегчается решение ДУ:
1.Для заданного ДУ и известного входного сигнала определяют изображение
(прямое преобразование Лапласа).
2.Решают уравнение в изображениях и переходят к оригиналу (обратное
преобразование Лапласа).

44.

4.Понятие устойчивости в ТАУ

45. 4.1. Дифференциальное уравнение. Характеристический полином.

В дальнейшем будем понимать исходным математическим описанием систем и отдельных
устройств линейные дифференциальные уравнения с постоянными коэффициентами.
dny
d n 1 y
d n 2 y
di y
dy
d mx
d m 1 x
d m 2 x
dix
dx
an n an 1 n 1 an 2 n 2 .... ai i .... a1
a0 y bm m bm 1 m 1 bm 2 m 2 ... bi i ... b1
b0 x
dt
dt
dt
dt
dt
dt
dt
dt
dt
dt
Или
n
a
i 0
i
y
i
m
bi x i
i 0
Если ввести оператор дифференцирования
dx
dkx
P x,
Pk x
k
dt
dt
исходное ДУ примет вид
(an P n an 1 P n-1 .... ai P i .... a1 P a0 ) y (bm P m bm 1 P m-1 .... bi P i .... b1 P b0 ) x
обозначим
A P (an P n an 1 P n-1 .... ai Pi .... a1 P a0 )
B P (bm P m bm 1 P m-1 .... bi Pi .... b1 P b0 )
A P y B P x

46.

Решение этого ДУ имеет вид
y t yсв t yвын t
где yсв t - свободная (переходная) составляющая, определяемая как решение однородного
уравнения
dny
d n 1 y
d n 2 y
di y
dy
an n an 1 n 1 an 2 n 2 .... ai i .... a1
a0 y 0
dt
dt
dt
dt
dt
или
A P y 0
Это однородное уравнение описывает свободное (автономное) движение системы при
отсутствии внешних воздействий.
Составляющая yвын t - вынужденная составляющая (установившийся процесс), определяется
внешними воздействиями и является частным решением неоднородного дифференциального
уравнения.

47.

Решение однородного дифференциального уравнения
dny
d n 1 y
d n 2 y
di y
dy
an n an 1 n 1 an 2 n 2 .... ai i .... a1
a0 y 0
dt
dt
dt
dt
dt
или
(a n P n a n 1 P n-1 .... ai P i .... a1 P a0 ) y 0
определяется как
n
n
i 1
i 1
А P 0
y t Ci e Pi t y i , где Pi корни уравнения A P 0
Тогда решение исходного дифференциального уравнения можно представить в виде
y t y св t
n
C
i 1
i
e
Pi t
n
y t ,
i 1
св i
где Pi корни уравнения A P 0.
На основании этого можно сделать вывод, что свободное движение в системе (или звене) может
быть представлено в виде суммы экспонент и зависит от показателей степени – корней
полинома
Поэтому, полином
называют характеристическим полиномом. Так как он
D P A P
«характеризует» (дает описание) собственные внутренние свойства системы или отдельного
звена.

48. 4.2. Понятие устойчивости.

Звено или система называются устойчивыми если свободная составляющая y св t
с ростом времени стремится к нулю.
Звено или система называются неустойчивыми если свободная составляющая y св t
с ростом времени неограниченно растет.
Звено или система находятся на границе устойчивости если предел свободной
составляющей y св t с ростом времени равен константе или не существует.
lim yсв t
t
0 ; устойчивая
; неустойчивая
const /еесущ; граница устойчивости

49. Рассмотрим возможное расположение корней характеристического полинома

4.3. Определение устойчивости
по корням характеристического полинома.
Рассмотрим возможное расположение корней характеристического полинома
D P an P n an 1 P n-1 .... ai P i .... a1 P a0 0
Im(P)
P1 α
P7
P2
P2,3 α jω
P5
P9
P4
P1
Re(P)
P4 0
P5,6 jω
P7,8 α jω
P3
P9 α
P6
P8

50.

Для каждого из возможных корней рассмотрим соответствующую ему составляющую свободного
движения
Pi α
yсв i Ci e α t
Pi,i 1 α jω
yсв i,i 1 Ci e α t sin ω t
Pi 0
yсв i Ci e0 t Ci
Pi,i 1 jω
yсв i,i 1 Ci e0 t sin ω t Ci sin ω t
Pi,i 1 α jω
yсв i,i 1 Ci e α t sin ω t
Pi α
yсв i Ci e α t

51.

Анализ рассмотренных случаев расположения корней характеристического полинома и
соответствующих ему переходных составляющих позволяет сделать следующие выводы:
если
Re Pi 0
если
Re Pi 0
- свободное движение или переходная составляющая неустойчива;
если Re Pi 0
- свободное движение или переходная составляющая находится на
границе устойчивости
- свободное движение или переходная составляющая устойчива;
Re Pi
0 , yсв i t ,
0 , yсв i t const / не сущ. ,
0 , yсв i t 0 .

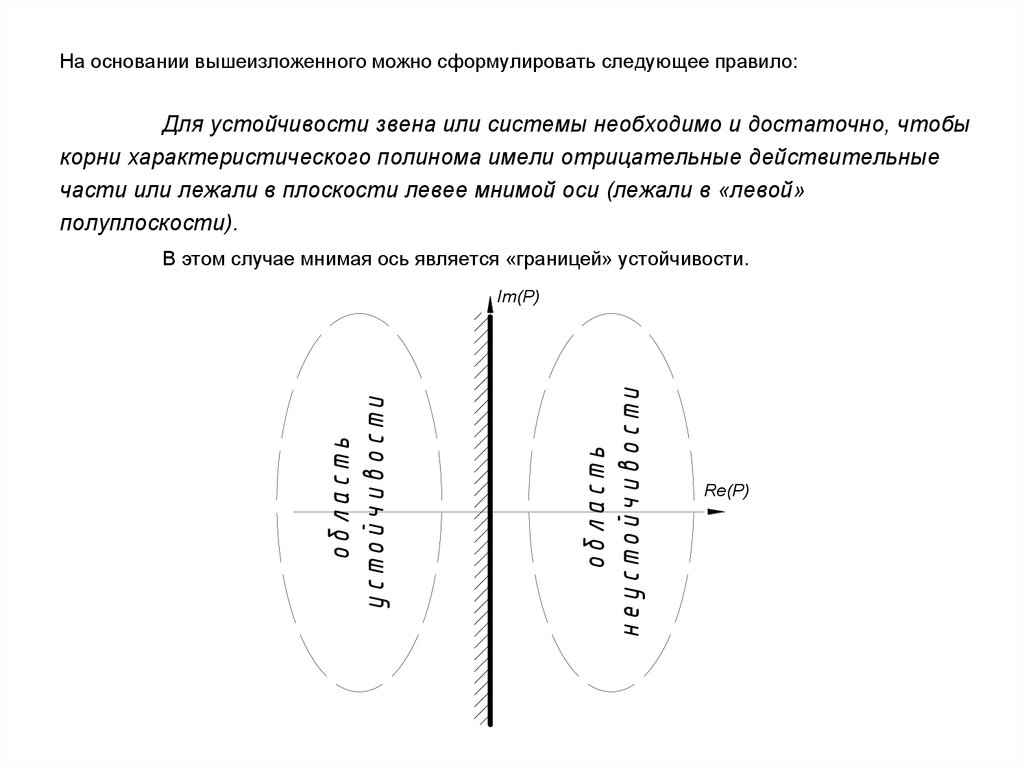
52.

На основании вышеизложенного можно сформулировать следующее правило:
Для устойчивости звена или системы необходимо и достаточно, чтобы
корни характеристического полинома имели отрицательные действительные
части или лежали в плоскости левее мнимой оси (лежали в «левой»
полуплоскости).
В этом случае мнимая ось является «границей» устойчивости.
Im(P)
Re(P)

53.

5. Понятие
передаточной функции

54.

Рассмотрим некоторый объект (звено) описываемый дифференциальным уравнением общего
вида.
an
dny
d n 1 y
d n 2 y
di y
dy
d mx
d m 1 x
d m 2 x
dix
dx
a
a
....
a
....
a
a
y
b
b
b
...
b
... b1
b0 x
n 1
n 2
i
1
0
m
m 1
m 2
i
n
n 1
n 2
i
m
m 1
m 2
i
dt
dt
dt
dt
dt
dt
dt
dt
dt
dt
Преобразуя это уравнение по Лапласу, получаем выражение через полиномы
an S n Y an 1 S n-1 Y .... ai S i Y .... a1 S Y a0 Y
bm S m X bm 1 S m-1 X .... bi S i X .... b1 S X b0 X
Y an S n an 1 S n-1 .... ai S i .... a1 S a0 X bm S m bm 1 S m-1 .... bi S i .... b1 S b0
Y A S X B(S)
Исходя из этого выражения можно определить изображение выходной величины Y S
Y S
bm S m bm 1 S m-1 .... bi S i .... b1 S b0
B(S)
X(S
)
X S
an S n an 1 S n-1 .... ai S i .... a1 S a0
A S
Передаточная функция – это отношение изображения выходной величины
Y S к изображению входной величины X S при нулевых начальных
условиях.
Y S
W S
X S

55.

Свойства передаточной функции.
Передаточная функция является полным аналогом дифференциального уравнения в области
изображений.
ДУ
ПФ
Знаменатель передаточной функции есть характеристический полином.
bm S m bm 1 S m-1 .... bi S i .... b1 S b0
B(S)
W S
an S n an 1 S n-1 .... ai S i .... a1 S a0
D S
D P an S n an 1 S n-1 .... ai S i .... a1 S a0
Для звена или системы с несколькими входами передаточная функция определяется по каждому
входному воздействию в отдельности.
X 1(S)
W1 S
X 2(S)
W2 S
X 3(S)
W3 S
Y1 S W1 S X 1(S)
Y2 S W2 S X 2(S)
Y1 S
Y2 S
Y3 S
Y S
Y3 S W3 S X 3(S)
Y S Y1 S Y2 S Y3 S

56.

Так же передаточная функция является инструментом для определения динамических
характеристик звеньев и систем.
ДУ
ПФ
Временные
характеристики
Частотные
характеристики

57.

6. Динамические характеристики

58.

Для оценки динамических свойств объектов, устройств, систем в целом
широко используют динамические характеристики.
Динамическая характеристика – реакция звена или системы
на некоторое стандартное или типовое входное воздействие.
По экспериментально полученным динамическим характеристикам можно
определить с достаточной степенью точности передаточную функцию.
Динамические характеристики делят на временные и частотные.

59. 6.1. Временные характеристики. 6.1.1. Импульсная (весовая) характеристика.

Импульсной (импульсной переходной) характеристикой t
называется реакция звена (или системы) на δ функцию при нулевых
начальных условиях.
Импульсная характеристика может быть найдена с помощью обратного преобразования
Лапласа:
ω t L 1 Y S L 1 W S X S
x t δ t
X S 1
Тогда, изображение выходного сигнала есть сама передаточная функция, а импульсная
характеристика является оригиналом передаточной функции.
ω t L 1 W S X S L 1 W S

60. 6.1.2. Переходная характеристика.

Переходной характеристикой h t называется реакция звена (или
системы) на единичное скачкообразное воздействие 1 t при нулевых
начальных условиях.
Переходная характеристика может быть найдена с помощью обратного преобразования
Лапласа:
h t L 1 Y S L 1 W S X S
x t 1 t
1
X S
S
W S
h t L 1 W S X S L 1
S
Если сравнить между собой изображение импульсной характеристики и переходной
W S
t L 1 W S
h t L 1
S
можно сказать: для того чтобы получить изображение импульсной характеристик, нужно
изображение переходной умножить на S . В области оригиналов умножение на S
соответствует операции дифференцирования. Можно сделать вывод , что импульсная
характеристика есть дифференциал переходной.
d h t
ω t
dt

61. 6.2. Частотные характеристики.

Частотными характеристиками называются формулы и графики,
характеризующие реакцию звена или системы на синусоидальное входное
воздействие в установившемся режиме, то есть вынужденные синусоидальные
колебания.
С помощью преобразования Фурье можно показать, что реакция
линейного звена или системы на синусоиду есть так же синусоида той же
частоты, что и входные колебания.
Установившаяся выходная синусоида отлична от входных колебаний по
амплитуде и имеет фазовый сдвиг.
Эти изменения амплитуды и фазы выходной синусоиды относительно входной в
зависимости от частоты (входной синусоиды) и описывают частотные
характеристики.

62.

Выражение
W jw A w e j w
носит название комплексной частотной характеристики или частотной
передаточной функции и представляет из себя амплитудно-фазо-частотную
характеристику (АФЧХ или АФХ) звена или системы.
Комплексная частотная характеристика может быть получена путем подстановки в
передаточную функцию S jω .
W j W S
S j

63.

Графически АФЧХ изображается на комплексной плоскости в координатах
годограф функции W j .
A, как
Формально, АФЧХ есть вектор на комплексной плоскости с длиной А и углом поворота
относительно действительной положительной полуоси.
С изменением частоты 0 ω
и называют АФЧХ.
конец вектора описывает некоторую кривую, которую
W j A e j Re ω j Im ω
Амплитудно-частотная характеристика
A – это модуль W j .
Представляет собой зависимость отношения амплитуды входной синусоиды к амплитуде
входной от частоты.
A ω W jω Re 2 ω Im2 ω
Фазово-частотная характеристика
- это аргумент
W j .
Представляет собой зависимость фазового сдвига между синусоидами от входной частоты.
arctg
ω arg W jω
arctg
Im ω
,
если Re ω 0
Re ω
Im ω
π , если Re ω 0
Re ω

64.

Связь частотных характеристик с декартовыми координатами:
Re ω A ω cos ω
Im ω A ω sin ω

65.

66.

8. Эквивалентные
преобразования соединения
звеньев

67.

Сложное соединение простых звеньев может быть преобразовано в более простые
соединения более сложных звеньев.
Предполагаем, что звенья являются направленными и их передаточные функции
независимы от их соединения.
Рассмотрим три вида соединения звеньев:
-последовательное;
-параллельное (параллельное согласное);
-с местной обратной связью (параллельное встречное).

68.

8.1 Последовательное соединение звеньев.
x t 1 t
1
X S
S
Y S
Wэкв S
X S
x t 1 t
1
X S
S
x t 1 t
1
X S
S
Y S W3 S Q S
Q S W2 S M S
M S W1 S X S
n
Y S W3 S W2 S W1 S X S
Y S П Wi S X S
i 1
n
Wэкв S П Wi S
i 1
x t 1 t
1
X S
S

69.

8.2 Параллельное соединение звеньев.
x t 1 t
1
X S
S
x t 1 t
1
X S
S
Y S
Wэкв S
X S
x t 1 t
1
X S
S
Y S Y1 S Y2 S Y3 S
Y1 S W1 S X S
Y2 S W2 S X S
Y3 S W3 S X S
Y S W1 S X S W2 S X S W3 S X S
Y S X S (W1 S W2 S W3 S )
n
Y S Wi S X S
i 1
n
Wэкв S Wi S
i 1
x t 1 t
1
X S
S

70.

8.3 Соединение с местной обратной связью.
x t 1 t
1
X S
S
x t 1 t
1
X S
S
Y S
Wэкв S
X S
x t 1 t
1
X S
S
Y S E S W1 S
E S X S Q S
Q S Wо.с. S Y S
Y S W S ( X S Wо.с. S Y S )
Y S W S X S W Wо.с. S Y S
1
1
1
Y S W1 Wо.с. S Y S W1 S X S
Y S (1 W1 Wо.с. S ) W1 S X S
Y S
W1 S
X S
1 W1 Wо.с. S
Wэкв S
W1 S
1 W1 Wо.с. S
x t 1 t
1
X S
S

71.

9. Характеристики
замкнутой линейной АСР

72.

Вычисление характеристик одноконтурной системы.
Замкнутая система является одноконтурной, если при ее размыкании в любой точке можно
получить цепочку из последовательно соединенных звеньев (не содержащую параллельных
и обратных связей.
Часто многоконтурную АСР можно привести к одноконтурной с помощью перестановки и
переноса узлов и сумматоров, эквивалентных преобразований.
Рассмотрим одноконтурную систему, сводящуюся к следующей структуре

73.

В этой системе два входных сигнала
x t - задание, и f t - возмущение.
Определим реакцию АСР на входной сигнал задания.
x t x t
f t 0
Y S ФЗ S X S
Выражение ФЗ S называется передаточной функцией замкнутой системы по заданию
ФЗ S
W S
W S
1 W S
B S
A S
W S Wрег S Wобупр S
B S
B S
A S
A S
B S
ФЗ S
Β S
A S Β S A S S
1
Α S
Α S

74.

Определим реакцию АСР на входной сигнал возмущения.
x t 0
f t f t
Y S Yу S Yв S
Y S Wобвозм S F S W S ( Y S )
Y S W S Y S Wобвозм S F S
Y S (1 W S ) Wобвозм S F S
Y S ФЗ X S
Y S
Wобв озм S
Фв S
F S
1 W S

75.

Кроме этих двух основных передаточных функций замкнутой системы часто используют
передаточную функцию замкнутой АСР по ошибке ФЕ S .
x t x t
f t 0
ФЕ S
E S
X S
E S X S Y S
E S X S E S W S
E S E S W S X S
E S (1 W S ) X S
ФЕ S
B S
W S
A S
E S
1
X S 1 W S
ФE S
1
1
A S
Β S
A S Β S A S S
1
Α S
Α S

76.

E S X S Y S X S (Yу S Yв S )
E S X S (ФЗ S X S Фв S F S )
E S ( X S ФЗ S X S ) Фв S F S
E S X S (1 ФЗ S ) Фв S F S
E S X S (1
E S X S
W S
) Фв S F S
1 W S
1
Фв S F S
1 W S
E S ФЗ X S Фв S F S