Similar presentations:
Электромеханические переходные процессы в энергосистемах и узлах нагрузки. Математические модели. Методы
1. Электромеханические переходные процессы в энергосистемах и узлах нагрузки
Математические моделиМетоды
доц., ктн. Шаргин Ю.М.
2. Моделирование вращающихся машин
23.
34. Системы координат
Фазные координаты a, b, c удобны для ввода исходных данныхи анализа результатов расчета статики и динамики в трехфазных
сетях. Однако системы уравнений, описывающие вращающиеся
машины (математические модели элементов), в этой системе
координат получаются весьма громоздкими, сложными, с
коэффициентами, являющимися функциями времени.
Поэтому при моделировании многомашинных схем вместо
фазных используют другие системы координат, которые позволяют
упростить запись уравнений вращающихся машин.
4
5. Системы координат
Переход от одних координатных осейк другим осуществляется при
.
помощи линейных преобразований.
Линейные преобразования уравнений состоят в том, что исходные
переменные в уравнениях заменяются новыми переменными,
линейно связанными с исходными. Число новых переменных равно
числу заменяемых переменных, поэтому для трехфазных
электрических схем число переменных в любых координатах
должно равняться трем. Например, для фазных токов
i x xa ia xb ib xc ic ,
i y ya ia yb ib ya ic ,
i z zaia zbib zcic .
xa xb xc
ya yb yc 0
za zb zc
где - коэффициенты линейного преобразования,
могут быть функциями времени, лишь бы определитель системы
уравнений в любой момент времени не равнялся нулю.
5
6. Системы координат
Системы фазных величин могут быть:симметричными,
несимметричными уравновешенными,
несимметричными неуравновешенными.
Сумма мгновенных значений уравновешенной системы фазных
величин равна нулю, а неуравновешенной – не равна нулю.
Симметричная система величин является уравновешенной.
На векторных диаграммах
уравновешенная и
неуравновешенная системы
фазных величин могут быть
изображены в виде тройки
векторов (токов, напряжений
потокосцеплений и др.),
проецируемых на линию
времени.
6
7. Системы координат
Система фазных величин, как угодно изменяющаяся во времени,но уравновешенная, может быть представлена проекциями
одного изображающего вектора на три фазные координатные оси,
сдвинутые на 120 эл. град., поскольку алгебраическая сумма
проекций вектора на такие оси всегда равна нулю.
Для установившихся режимов модуль и скорость вращения
изображающего вектора постоянны.
7
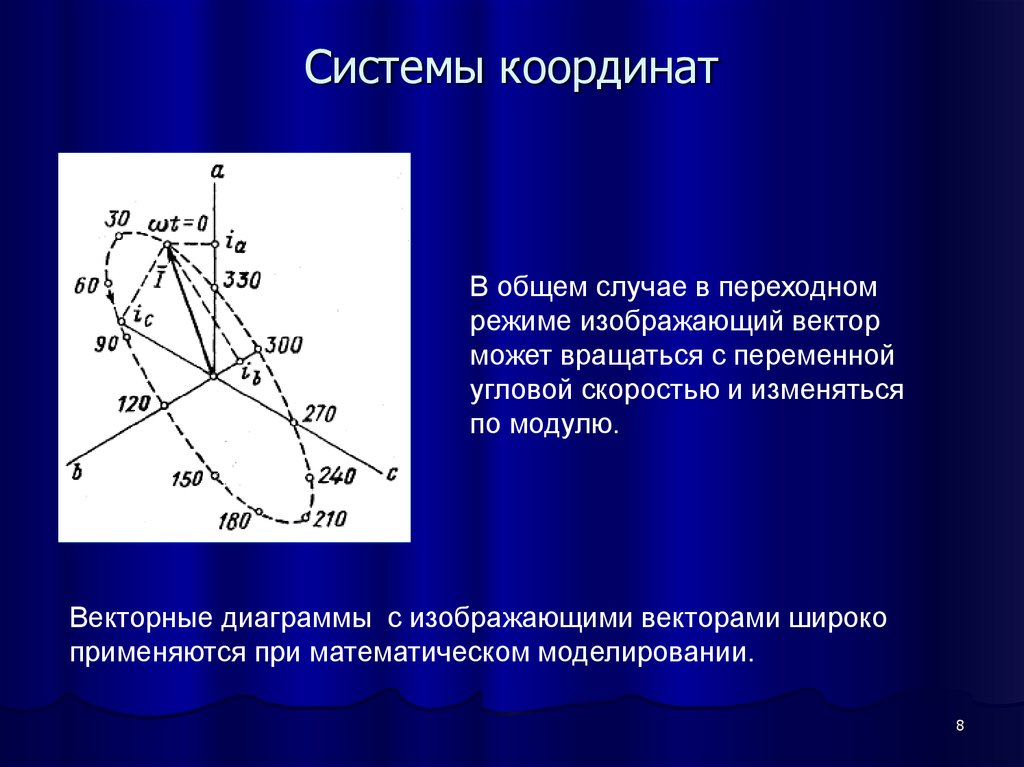
8. Системы координат
В общем случае в переходномрежиме изображающий вектор
может вращаться с переменной
угловой скоростью и изменяться
по модулю.
Векторные диаграммы с изображающими векторами широко
применяются при математическом моделировании.
8
9. Системы координат
Неуравновешенную систему фазных величин можно привестик уравновешенной путем выделения нулевой составляющей.
Нулевая составляющая является новой независимой
переменной, при этом одна из фазных переменных должна быть
исключена, поскольку является зависимой от двух других и
нулевой составляющей. Например, нулевая составляющая
неуравновешенной системы фазных токов равна
i0
1
ia ib ic
3
ia ia i0 , ib ib i0 , ic ic i0
Уравновешенная система
фазных токов, ia’, ib’, ic’, т. к.
ia ib ic ia ib ic 3i0 0
Одну из этих новых переменных, зависимую от двух других
и нулевой составляющей в соответствии с условием
уравновешенности системы, необходимо исключить,
обычно исключают ic’.
9
10. Системы координат
Выделение нулевой составляющей является линейнымпреобразование токов из фазной системы координат a, b, c
в косоугольную систему координат a’, b’, 0
2
1
1
ia ia ib ic ,
3
3
3
1
2
1
ib ia ib ic ,
3
3
3
1
i0 ia ib ic .
3
Теперь можно рассматривать новые
переменные ia’, ib’, i0 как проекции
изображающего вектора тока на оси
I
a’, b’, расположенные под углом
120 эл. град.
Выделение нулевой составляющей лежит в основе
преобразования переменных из фазной системы координат в
неподвижную или вращающуюся прямоугольную систему координат.
Вместо косоугольных осей удобно ввести прямоугольную систему
координат и новые переменные, которые являются проекциями
изображающего вектора на ортогональные оси.
10
11. Системы координат
Линейное преобразование переменных с выделением нулевойсоставляющей имеет следующие свойства:
• нулевая составляющая равна нулю в случае, если рассматриваемая
система фазных величин является уравновешенной. Следовательно, для
уравновешенных систем число независимых переменных сокращается до
двух, т. к. если сумма трех величин равна нулю, то, зная две переменные,
всегда можно найти третью;
• нулевые составляющие токов и потокосцеплений не участвуют в
формировании электромагнитного момента вращающихся машин.
В задачах, связанных с исследованием движения синхронных и
асинхронных машин, при определении электромагнитного момента
машины можно не рассматривать нулевые составляющие переменных.
Однако для преобразования переменных к фазным координатам нулевую
составляющую необходимо определить;
• для уравновешенной системы величин в качестве переменных можно
рассматривать не только проекции изображающих векторов на
координатные оси, а пойти дальше, и рассматривать в качестве
переменных сами изображающие векторы. Если система переменных не
уравновешена, можно рассматривать совместно векторное уравнение и
уравнение для нулевых составляющих переменных.
11
12. Системы координат
Выбор координат при записи уравнений элементов энергосистемопределяется удобством решения тех или иных задач.
Если схема не содержит вращающихся машин, уравнения линий
и трансформаторов наиболее просто записываются в
прямоугольной неподвижной системе координат α, β, ось α
совмещается с осью а.
Для моделирования схем, содержащих вращающиеся машины,
применяют вращающиеся прямоугольные системы координат:
• оси d, q, жестко связанные с ротором машины (собственные оси),
• оси ds, qs - синхронные координатные оси , вращающиеся с
синхронной угловой скоростью s = 2 f = 314,159 эл. радиан/с,
• оси dv, qv, вращающиеся с произвольной угловой скоростью v и
имеющие относительно синхронных осей скольжение sv.
В названии систем координат про нулевую составляющую обычно не
упоминают, ее существование подразумевается.
12
13.
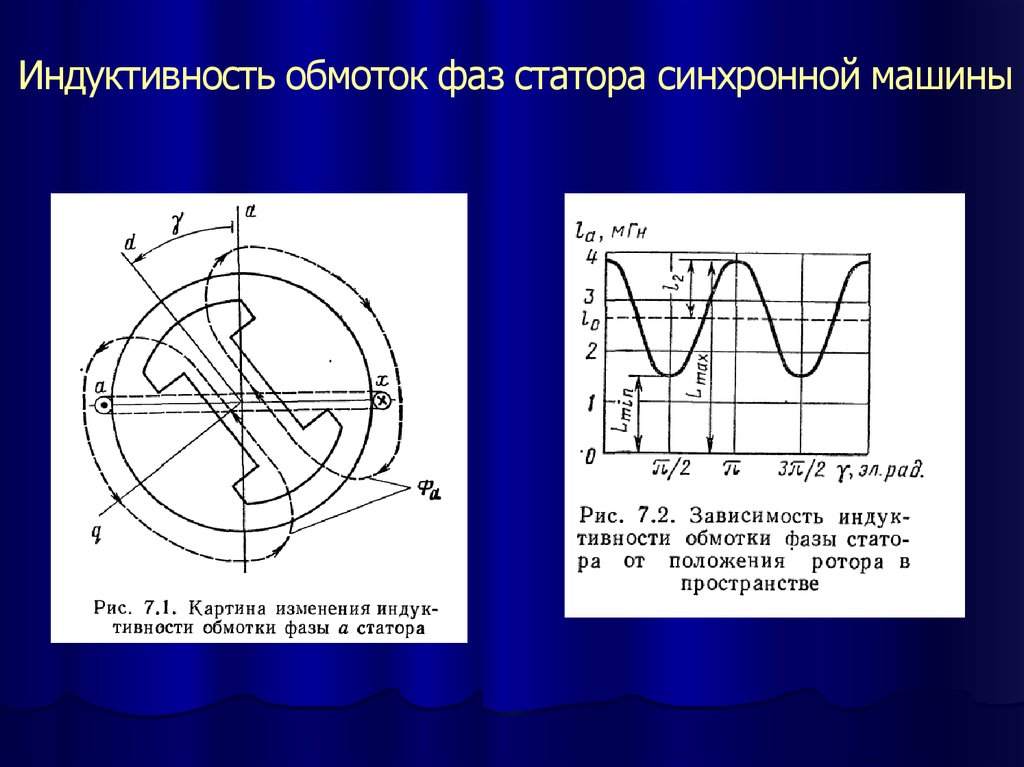
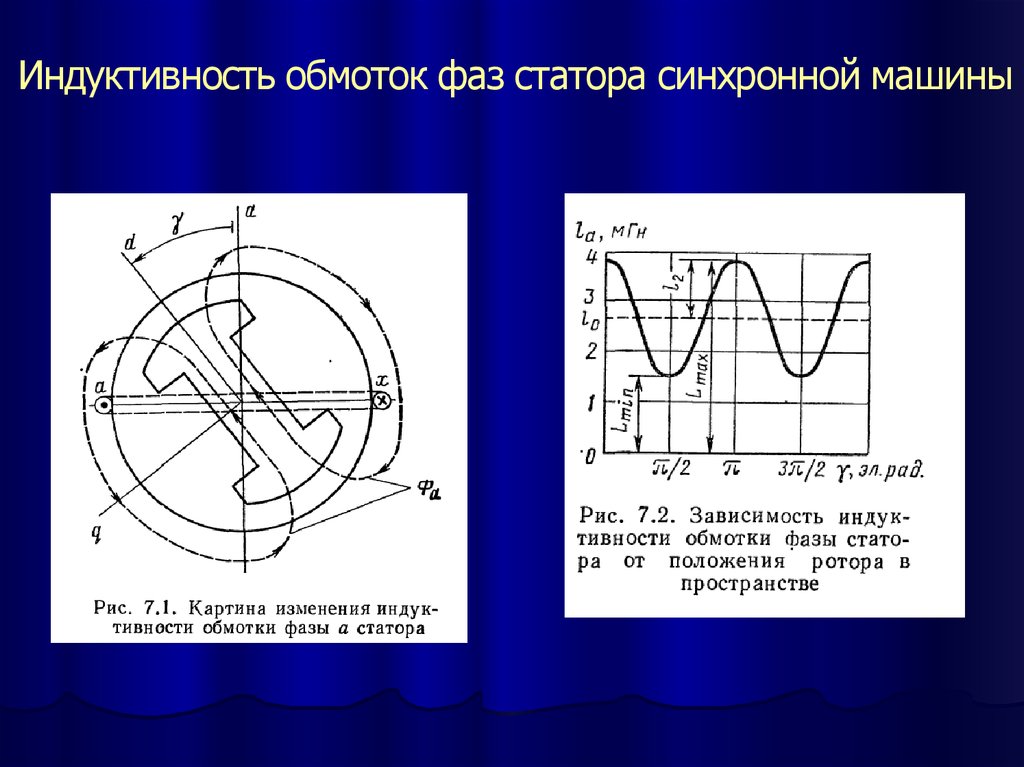
Индуктивности обмоток фаз статора синхронной машины14.
Индуктивность обмоток фаз статора синхронной машины15.
Взаимные индуктивности обмоток фаз статора.16.
Преобразование переменных и уравнений(Преобразование Блонделя)
17. Системы координат
При моделировании многомашинных схем возникаетнеобходимость преобразования переменных из одной системы
координат в другую при помощи линейных преобразований.
Например, при расчете электрического режима в схеме
осуществляется переход к осям, общим для всех элементов
рассматриваемой схемы, с возвратом к собственным осям при
расчете режима самой машины.
В качестве общих осей можно выбрать синхронные оси ds, qs
или оси dv, qv.
Чтобы осуществить преобразование переменных к общим осям
и обратно, необходимо знать угол между координатными осями,
поэтому математическая модель машины должна иметь уравнение
для определения углов между осями, в которых записаны
уравнения машины, и общими координатными осями. Если
уравнения машины записаны в общих осях, необходимость в таких
преобразованиях отпадает.
17
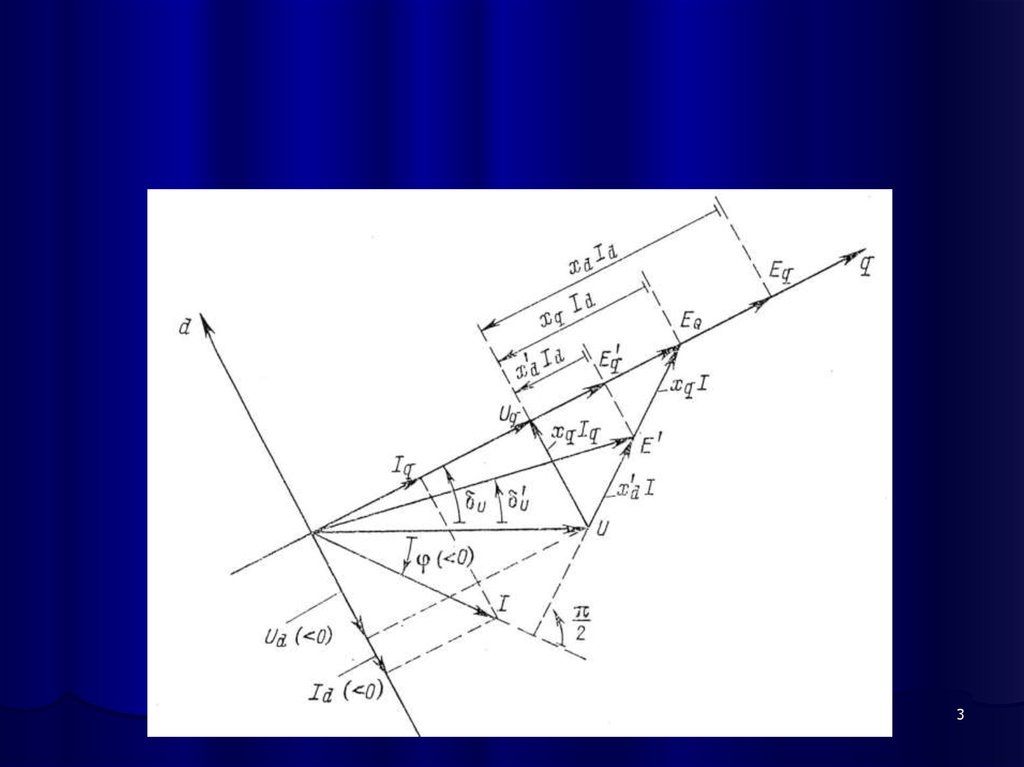
18. Системы координат
Вращающиеся оси можно совместить с осями комплекснойплоскости, причем ось q совмещается с осью вещественных, а ось
d – с осью мнимых. При этом изображающие векторы являются
также комплексами, что позволяет проводить вычисления в
комплексном виде.
Совмещение осей позволяет связать переменные,
используемые в алгоритмах расчета установившихся режимов с
переменными, фигурирующими в расчетах переходных процессов,
при помощи векторных диаграмм.
18
19. Соглашения при записи уравнений
При записи уравнений принимаем, что:• положительным направлением вращения изображающих
векторов и координатных осей является направление вращения
против часовой стрелки;
• положительным направлением отсчета углов является
направление против часовой стрелки;
• ось d упреждает ось q при вращении осей против часовой
стрелки;
• знак плюс имеют переменные, являющиеся проекциями
изображающего вектора на положительное направление осей
d или q, знак минус имеют переменные при проецировании
вектора на отрицательное направление осей;
• углы между вращающимися d, q осями определяются между
одноименными осями;
• знак скольжения имеет знак первой производной угла по
времени;
• время и инерционные постоянные выражаются в секундах;
• используется система относительных единиц А.А. Горева.
19
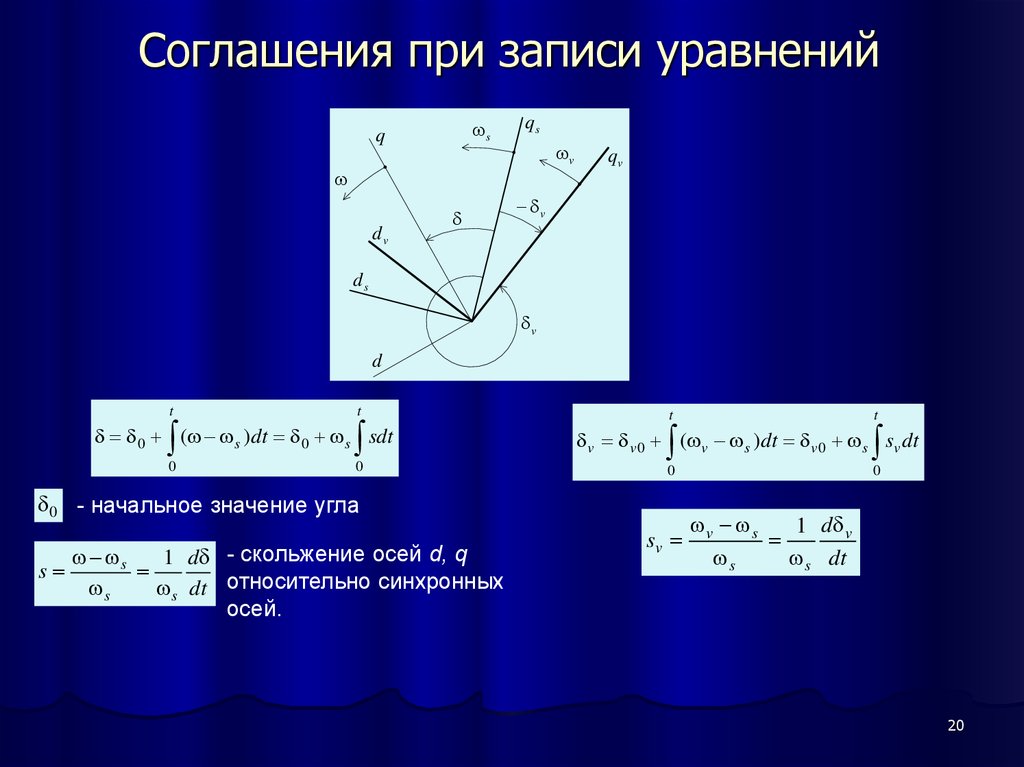
20. Соглашения при записи уравнений
sq
qs
v
dv
qv
v
ds
v
d
t
t
0
0
0 ( s )dt 0 s sdt
t
0
0
v v 0 ( v s )dt v 0 s sv dt
0 - начальное значение угла
s
s
1 d - скольжение осей d, q
s
s dt относительно синхронных
t
sv
v s
1 d v
s
s dt
осей.
20
21. Линейное преобразование переменных
A A , E,U , I , Jq
v
qv
A
dv
Aqv
Aq
Ad
d
Adv
t
t
0
0
0 ( v )dt 0 s ( s sv )dt
Adv Ad cos Aq sin ,
Aqv Aq cos Ad sin .
Ad Adv cos Aqv sin ,
Aq Aqv cos Adv sin .
Переменные в данной системе координат являются проекциями на оси
изображающего вектора или суммой проекций на рассматриваемые оси
составляющих вектора в другой системе координат.
21
22. Уравнение движения генератора
Принятые соглашения, формулы для определения скольжений ипреобразования координат соответствуют генераторной форме записи
уравнений якоря машины.
Уравнение движения ротора машины должно быть согласовано с
генераторной формой записи уравнений якоря.
d
m
F
J
i
dt
(i )
J – момент инерции ротора
– момент внешней силы
m Fi
Fi
– абсолютная угловая скорость
Mт Me M0 J
d
dt
M т 0 момент механической силы, создается первичным двигателем
M e 0 электромагнитный момент
M 0 0 момент сил трения
22
23. Запись уравнений АД и СД
1 вариант. Нормальным режимом работы синхронных иасинхронных двигателей является режим потребления активной
мощности из сети, поэтому обычно двигатели рассматривают как
приемники электрической энергии, положительными становятся
активная мощность, потребляемая из сети, и момент. При этом
необходимо также изменить формулу расчета скольжения двигателя,
чтобы скольжение было положительным при угловой скорости ротора
меньше синхронной
s
s
s
при сохранении положительного направления отсчета углов
отсчитывать углы между координатными осями от собственных осей к
общим осям, а внутренний угол синхронного двигателя
U ^ E Q
отсчитывать против часовой стрелки от вектора ЭДС к вектору
напряжения, чтобы активная мощность, потребляемая из сети, была
положительной.
23
24. Запись уравнений АД и СД
Уравнение движения записывается таким образом, чтобы знакэлектромагнитного момента соответствовал знаку активной
мощности
M e M мх M 0 J
d
dt
Me 0
электромагнитный момент на валу, создаваемый двигателем
M мх 0
механический момент на валу, создаваемый механизмом
M0 0
момент сил трения
Если момент двигателя станет меньше момента механизма, появится
отрицательное угловое ускорение, увеличится положительное значение
скольжения и угла, возрастет положительная активная мощность,
потребляемая из сети, и наоборот.
Знак углового ускорения не соответствует знаку второй производной угла
по времени, поскольку в двигательном режиме внутренний угол принят
положительным. Указанную противоречивость знаков нужно учитывать при
обработке модели двигателя в алгоритмах и программах расчета переходных
процессов.
24
25. Запись уравнений АД и СД
2 вариант. Можно применить генераторную форму записиуравнений статора двигателей. Тогда в основном двигательном
режиме активная мощность, электромагнитный момент на валу, угол
и скольжение будут отрицательными величинами.
Чтобы получить правильный знак углового ускорения,
соответствующий второму закону динамики для вращательного
движения, скольжения и угла, в уравнении движения необходимо
механический момент на валу, создаваемый механизмом, тоже
считать отрицательным. Форма записи уравнения движения
двигателя по сравнению с генератором не изменяется
M мх
d
Me M0 J
dt
M e 0 M мх 0
M0 0
Если по абсолютной величине момент двигателя станет меньше момента механизма,
появится отрицательное угловое ускорение, увеличится отрицательное значение
скольжения и угла, возрастет мощность, потребляемая из сети (увеличится
абсолютное значение отрицательного значения мощности), и наоборот. Этот способ
записи уравнений является нетрадиционным, но не имеет внутренней
противоречивости.
25
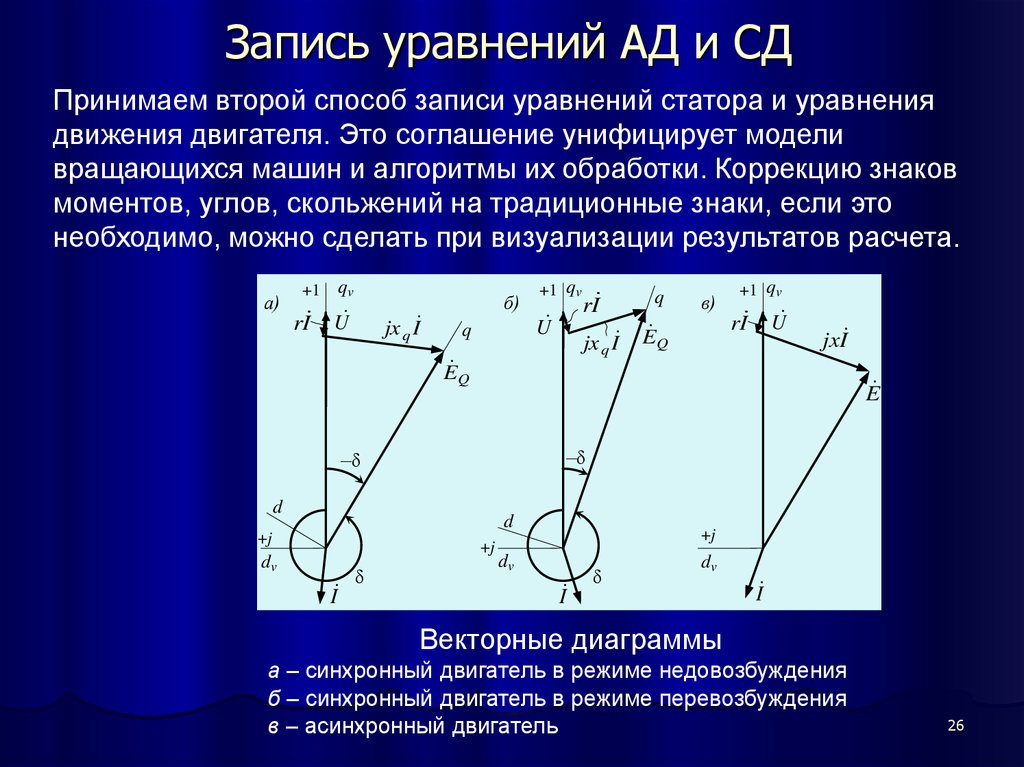
26. Запись уравнений АД и СД
Принимаем второй способ записи уравнений статора и уравнениядвижения двигателя. Это соглашение унифицирует модели
вращающихся машин и алгоритмы их обработки. Коррекцию знаков
моментов, углов, скольжений на традиционные знаки, если это
необходимо, можно сделать при визуализации результатов расчета.
а)
+1
qv
rI U
jx q I
б)
q
+1 qv
U
rI
d
+j
I
rI U
jxI
–δ
d
δ
+1 qv
E
–δ
dv
в)
jx q I EQ
E Q
+j
q
+j
dv
I
δ
dv
I
Векторные диаграммы
а – синхронный двигатель в режиме недовозбуждения
б – синхронный двигатель в режиме перевозбуждения
в – асинхронный двигатель
26
27.
Индуктивности обмоток фаз статора синхронной машины28.
Индуктивность обмоток фаз статора синхронной машины29.
Взаимные индуктивности обмоток фаз статора.30.
Преобразование переменных и уравнений(Преобразование Блонделя)
31. Уравнения Парка-Горева и их использование
Уравнения Парка-Горева описывают идеализированную машину вовращающихся собственных d, q осях и базируются на следующих
основных допущениях:
1. Магнитная проницаемость стали машины принимается равной
бесконечности. Это позволяет однозначно определить картину
магнитного поля от какой-либо обмотки машины и использовать
принцип наложения при определении магнитного поля в зазоре
машины.
31
32. Уравнения Парка-Горева и их использование
2. Распределение магнитных полей самоиндукции трехфазныхобмоток и взаимоиндукции обмоток статора и ротора вдоль
окружности машины считается синусоидальным с
пространственным полупериодом, равным полюсному делению.
Таким образом, принимается в расчет лишь первая (основная)
гармоника указанных полей и не учитывается влияние зубцовых
полей в зазоре, обусловленных зубчатостью статора и ротора, а
также высших и субгармоник поля, вызванных соответствующими
гармониками магнитодвижущих сил обмоток статора и ротора.
Основанием для подобного упрощения является способность
трехфазной обмотки «фильтровать» высшие гармоники поля в
зазоре. В нормально спроектированной машине удается получить
высшие гармоники ЭДС, обусловленные рядом высших гармоник
поля, весьма малой амплитуды. Рассматриваемое допущение
означает также пренебрежение участием высших гармоник в
образовании электромагнитного момента.
32
33. Уравнения Парка-Горева и их использование
3. Принятая идеализация картины магнитного поля предполагает,что магнитопровод и обмотки машины симметричны. Это значит, что
магнитопровод имеет одинаковые очертания на всех полюсных
делениях, а в пределах полюсного деления симметричен
относительно осей d и q. Это также значит, что в трехфазной
обмотке все фазные обмотки имеют одинаковое число витков,
активные сопротивления и взаимный сдвиг магнитных осей,
стержни демпферной системы симметричны относительно осей
d и q, а обмотка возбуждения идентична на всех полюсах ротора.
33
34. Уравнения Парка-Горева и их использование
4. Демпферная система явнополюсных машин или бочка роторанеявнополюсных машин замещается двумя эквивалентными
контурами, по одному в оси d и в оси q, с постоянными
параметрами.
5. Предполагают, что в продольной и поперечной осях машины
кроме потоков рассеяния существуют единые потоки взаимной
индукции, пронизывающие все контуры, расположенные по
соответствующим осям машины.
34
35. Уравнения Парка-Горева и их использование
Второе, третье и пятое допущения для энергетических машинявляются общепринятыми и практически не влияют на точность
модели. Пятое допущение заметно упрощает запись уравнений и
лежит в основе методов определения параметров модели по
каталожным данным генераторов.
Первое и четвертое допущения налагают ограничения на
использование классических уравнений Парка-Горева для
математического моделирования многомашинных электрических
схем, поскольку модель вращающихся машин не полностью
отображает свойства самих объектов, что может приводить к
заметным и недопустимым погрешностям.
35
36. Математическая модель синхронного генератора
Для синхронной машины, имеющей на роторе обмотку возбуждения,произвольное количество 0…nd эквивалентных короткозамкнутых контуров
в оси d и произвольное количество 0…nq эквивалентных короткозамкнутых
контуров в оси q, уравнения Парка-Горева в именованных единицах можно
записать в следующем виде.
Статор (якорь)
Ротор
d d
q rid u d
dt
d
d q
dt
riq uq
d r
rr ir E r
dt
d rdi
rrdiirdi 0
dt
d rqk
dt
rrqk irqk 0
i 0...nd
k 0...nq
36
37. Математическая модель синхронного генератора
ndd Ld id M ad ir M ad irdi
i 1
nq
q Lq iq M aq irqk
k 1
nd
3
r M ad id Lr ir M ad irdi
2
i 1
rdi
3
M ad id Lrdiirdi M ad ir M ad
2
rqk
q
3
M aqiq Lrqk irqk M aq irqj
2
j 1,
nd
irdj
j 1,
j i
i 0...nd
n
k 0...nq
j k
J
d
3
M т d iq q I d
dt
2
37
38. Система относительных единиц А.А. Горева
Статор (якорь)I б 2I ф.н
U б 2U ф.н
3
S б S н 3U ф.н I ф.н U б I б
2
б s 2 f н 314 ,159 эл. рад./с
zб
Uб
Iб
Mб
Lб
zб
б
б Lб I б
Sб p
б
Uб
б
38
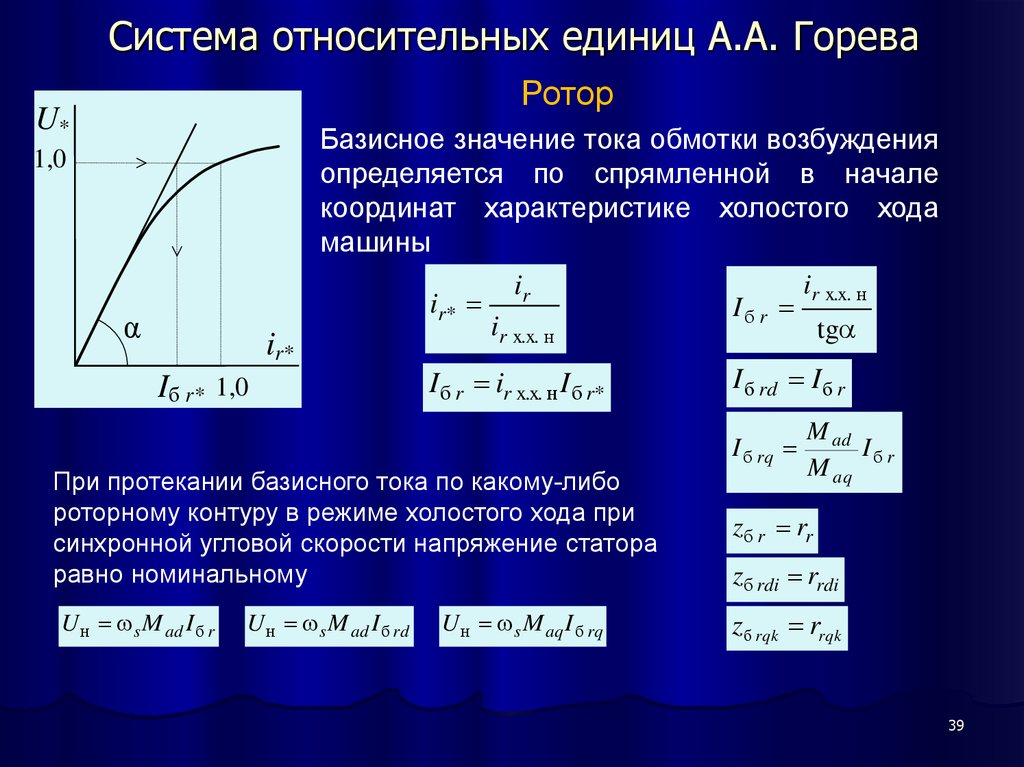
39. Система относительных единиц А.А. Горева
РоторU*
1,0
α
ir*
Базисное значение тока обмотки возбуждения
определяется по спрямленной в начале
координат характеристике холостого хода
машины
ir x.x. н
ir
ir *
Iб r
ir x.x. н
tg
Iб r* 1,0
I б r ir x.x. н I б r*
I б rd I б r
I б rq
При протекании базисного тока по какому-либо
роторному контуру в режиме холостого хода при
синхронной угловой скорости напряжение статора
равно номинальному
U н s M ad I б r
U н s M ad I б rd
U н s M aq I б rq
M ad
Iб r
M aq
zб r rr
zб rdi rrdi
zб rqk rrqk
39
40. Математическая модель синхронного генератора
1 d d(1 s) q rid u d
s dt
1 d q
(1 s ) d
riq u q
s dt
d r
1
Er Eq
dt
Tr
d rdi
dt
d rqk
dt
1
Erqi
Trdi
1
Trqk
Erdk
i 0...nd
k 0...nq
ds 1
M т M e
dt TJ
d
s s sv
dt
40
41. Математическая модель синхронного генератора
xd xad xsnd
d xd id Eq Erqi
i 1
xq xaq xs
xad , xaq
xs
xr xad xsr xrdi xad xsrdi xrqk xaq xsrqk
nq
q xq iq Erdk
xsr , xsrdi , xsrqk
k 1
2
xad
x
r
id Eq ad
xr
xr
rdi
nd
Erqi
i 1
Eq
s M ad ir
s M ad I б r
nd
xad
id E rqi
E q E rqj i 0...nd
xrdi
xrdi
j 1
j
i
rqk
2
xad
2
xaq
xrqk
iq Erdk
M e d iq q id
xaq
xrqk
nq
Erdj
j 1
j k
k 0...nq
E rqi
s M ad irdi
s M ad I б rd
Tr
Erdk
s M aqirqk
s M aq I б rq
Lr
x
r
rr
s rr
Trdi
Lrdi
x
rdi
rrdi s rrdi
Trqk
Lrqk
TJ J
rrqk
xrqk
s rrqk
2s
Sб p 2
41
42. Модификация уравнений роторных контуров
2xad
d
xr xd
r
rdi
rr
1
xr sTr
2
xad
xrdi xd
rdi
rqk
rr
1
xrdi sTrdi
gr
xad
xr
d rdi
s rdi Erqi
dt
dt
s rqk Erdk
xrqk x q
rqk
g rdi
d r
s r ( Er Eq )
dt
d rqk
2
xaq
xad
xrdi
коэффициенты магнитной связи обмотки
возбуждения и эквивалентных демпферных
контуров со статорными контурами
rr
1
xrqk sTrqk
g rqk
xaq
декременты роторных контуров
магнитные параметры
xrqk
nd
r d xd id Eq g r Erqi
i 1
rdi
nd
rdi xd id E rqi g rdi E q E rqj
j 1
j
i
nq
rqk rqk xq iq Erdki g rqk Erdj
j 1
j k
42
43. Учёт насыщения стали
Для учета зависимости коэффициентов взаимной индукции исоответствующих реактивностей от насыщения стали в
исходные
уравнения
машины
вводятся
специальные
переменные параметры d и q, учитывающие насыщение
стали по осям d и q. Сами же коэффициенты и реактивности
взаимной индукции являются постоянными параметрами, не
зависящими
от
насыщения,
и
определяются
для
идеализированной, ненасыщенной машины.
Параметры насыщения d и q являются функцией ЭДС за
реактивностью рассеяния статора
Характеристика насыщения
E E q jE d
nd
E q xad id Eq Erqi
i 1
E d
nq
xaqiq E rdk
k 1
Неявнополюсная машина
d q ( E )
E E 2q E 2d
Явнополюсная машина
d d ( E q )
43
44. Учёт насыщения стали
Дляучета
насыщения
стали
необходимо
преобразовать
алгебраические уравнения для потокосцеплений таким образом, чтобы в
них фигурировали продольная и поперечная составляющие ЭДС за
реактивностью рассеяния статора, и ввести в уравнения машины
параметры насыщения
nd
d xs id xad id Eq Erqi xs id E q
i 1
nq
q xs iq xaqiq Erdk xs iq E d
k 1
2
xad
x
r
id Eq ad
xr
xr
nd
Erqi
i 1
x
ad
xr
nd
xsr
xad
x
r
xad id
E
Eq
Eq Erqi Eq Eq
q
x
xr
xr
i 1
ad
rdi
nd
xad
xrdi
E rqi E q E rqj Erqi E rqi
xad id
xrdi
xad
j 1
j i
rqk
nq
xaq
xsrqk
xaq
xrqk
E d
Erdk
Erdk Erdj Erdk E rdk
xaqiq
xrqk
xaq
x
x
j 1
rqk
rqk
j k
xad
x
E q srdi Erqi
xrdi
xrdi
44
45. Учёт насыщения стали
Ввод параметров насыщения в уравнения машины рассмотрим напримере обмотки возбуждения.
nd
3
r M ad id Lr ir M ad irdi
2
i 1
d
M ad
M ad
M ad d M ad
Lr Lsr M ad Lsr d M ad
nd
d 3
d M ad id Lsr ir d M ad ir d M ad irdi rr ir Er
dt 2
i 1
Умножим на
s M ad
Lr
, введём
Eq s M ad ir
, приведём к о. е. А.А. Горева
d r 1
1
Eq Er
dt
Tr
Tr
U б s M ad
Uб r
rr
Uб
nd
x
xad
x
x
r
d xad id Eq Erqi sr Eq ad E q sr Eq
x
xr
xr
xr
i 1
r
E q
nd
d xad id Eq Erqi
i 1
Выражение для потокосцепления не изменились. Изменилось лишь
выражение для поперечной составляющей ЭДС за реактивностью рассеяния
статора, в него теперь входит параметр насыщения.
45
46. Учёт насыщения стали
Модель генератора в собственных d, q осях, в о.е. А.А Горева, с учётомнасыщения стали по пути магнитного потока взаимной индукции, с многоконтурной схемой замещения ротора, пригодная для проведения расчетов переходных процессов в энергосистемах и в узлах нагрузки, принимает вид:
1 d d
( 1 s ) q rid u d
s dt
(1 s ) d
1 d q
riq u q
s dt
d r
1
( Er Eq )
dt
Tr
d rdi
1
Erqi
dt
Trdi
d rqk
dt
1
Trqk
Erdk
i 0...nd
k 0...nq
ds 1
M т M e
dt TJ
d
s s sv
dt
46
47. Учёт насыщения стали
d xs id E qq xs iq E d
r
xad
x
E q sr Eq
xr
xr
rdi
xad
x
E q srdi Erqi
xrdi
xrdi
rqk
xaq
xrqk
E d
xsrqk
xrqk
i 0...nd
Erdk k 0...nq
E q d xad id Eq Erqi
i 1
nd
E d
nq
q xaqiq E rdk
k 1
M e d iq qid E qiq E d id
Неявнополюсная машина
d q ( E )
E E 2q E 2d
Явнополюсная машина
q 1
d d ( E q )
47
48. Характеристика насыщения
Характеристику насыщения стали машины можно построить по заданнойхарактеристике холостого хода.
В установившемся режиме холостого хода ток статора и токи демпферных контуров
равны нулю, ЭДС, индуктируемые в контурах статора магнитным полем токов
демпферных контуров, тоже равны нулю, поэтому
d E q Eq
q 0
Статорные уравнения машины в установившемся режиме холостого хода принимают вид
d Eq U q U
U
Eq
Ud 0
Eq
Eq[и.е.]
Uб
s M ad ir
ir
tg ir*
s M ad I б r ir х.х . н
tg
Следовательно, зная характеристику холостого хода, заданную как таблицу пар
значений , можно построить характеристику насыщения , представляющую собой
таблицу пар значений , по формулам
U*
U
E q tg ir *
E Eq tg ir*
48
49. Упрощённые уравнения синхронного генератора
При решении практических задач уравнения синхронной машины можно упростить. Вможно исключить трансформаторные ЭДС .
d q
d d
dt
dt
При этом нагрузка и статические сетевые элементы электрической схемы тоже
должны моделироваться упрощенно, из их уравнений также исключаются
трансформаторные ЭДС. Современные исследования подтверждают правомерность
применения упрощенных уравнений Парка-Горева в расчетах динамики энергосистем.
1 s q rI d
U d
r 0
1 s d rI q U q
Пренебрегают также ЭДС скольжения
1 s q U d
1 s d U q
s d
s q
q U d
d U q
49
50. Замещение синхронной машины источником ЭДС
Для представления генератора источником ЭДС нужно выполнитьследующие преобразования:
1. Из уравнений для потокосцеплений контуров ротора выразить ЭДС E q Erqi Erdk
и подставить их в уравнения для E q и E d .
2. Полученные выражения для поперечной и продольной составляющих ЭДС
подставить в уравнения для d и q .
3. Развернутые выражения для d, q –составляющих потокосцеплений
подставить в упрощенные статорные уравнения и преобразовать эти уравнения
к форме записи уравнений для источника ЭДС.
Из-за несимметрии генератора по осям d и q источник ЭДС, замещающий
генератор, можно представить в общем виде матричным уравнением
Eqe
jE de
Uq
jU d
r
jx de
jx qe
r
Iq
jI d
Eqe U q rI q xde I d
Ede U d xqe I q rI d
50
51. Упрощенные уравнения синхронного генератора
Однако упрощенная модель вращающихся машин не полностью отображаетсвойства самих объектов. Упрощенная модель теряет способность
воспроизводить электромагнитные переходные процессы, возникающие при
коммутациях в схеме, поэтому токи статора генераторов, двигателей и токи
сетевых элементов, а также напряжения в узлах схемы при возникновении
коротких замыканий, включении/отключении линий теперь могут изменяться
скачком.
В решении упрощенной системы уравнений генератора при коммутациях в сети
отсутствуют свободные составляющие токов статора и, следовательно, не
воспроизводятся ударные токи и моменты на валу, а также не учитывается
асинхронный момент, возникающий при вращении ротора относительно
неподвижного в пространстве магнитного поля, созданного апериодическими
токами статора. Ввиду значительной инерции вращающихся масс генерирующих
агрегатов и быстрого затухания свободных составляющих токов статора эти
моменты не оказывают заметного влияния на движение агрегата. Апериодическую
составляющую электромагнитного момента рекомендуется учитывать для
капсульных гидрогенераторов при возникновении близких коротких замыканий.
51
52. Замещение синхронной машины источником ЭДС
Преобразования дают следующие выражения для d, q составляющихэквивалентной ЭДС, индуктируемой в контурах статора магнитным полем токов
роторных контуров:
E qe
i nd
xr
xad
xrdi
1 s
r
rdi ,
xad x sr
x
i 1 srdi
Ede 1 s
xaq
xaq
k nq
xrqk
x
k 1
rqk ,
srqk
xde 1 s xs xad
xqe 1 s xs xaq
xad
1
1
1
d xad xsr
nd
x
i 1
xaq
1
srdi
1
nq
1
1
q xaq k 1 x srqk
52
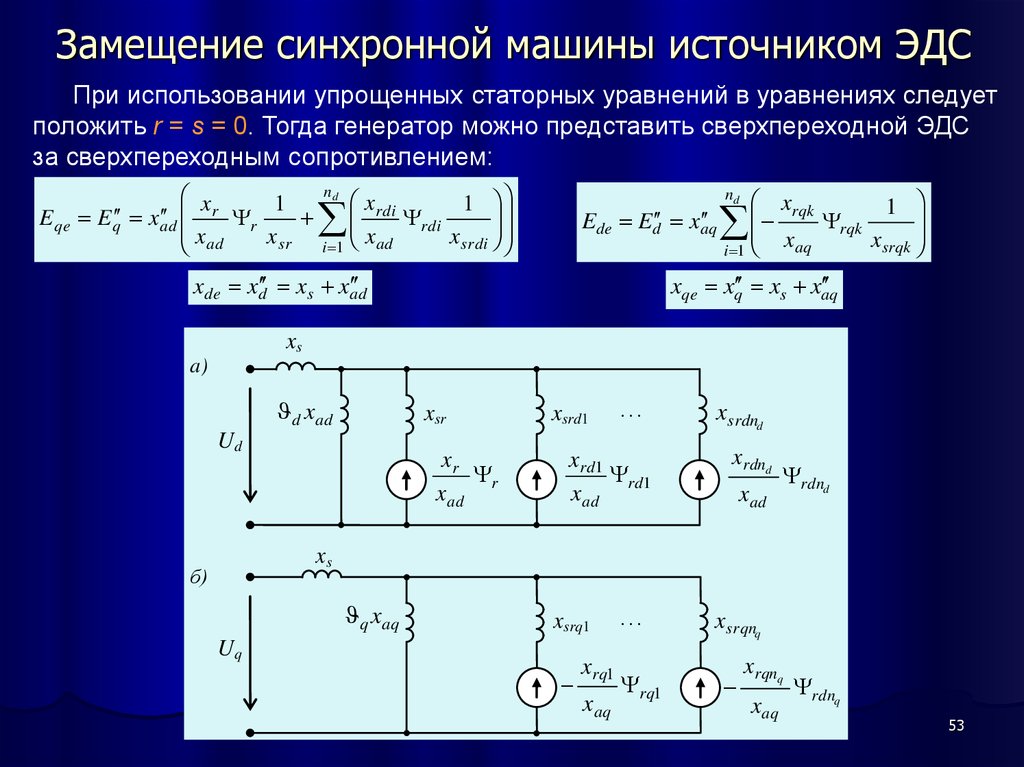
53. Замещение синхронной машины источником ЭДС
При использовании упрощенных статорных уравнений в уравнениях следуетположить r = s = 0. Тогда генератор можно представить сверхпереходной ЭДС
за сверхпереходным сопротивлением:
Eqe
x
1
r r
Eq xad
xad
x sr
xrdi
1
x rdi x
srdi
i 1 ad
nd
xrqk
1
Ed xaq
xaq rqk xsrqk
i 1
nd
Ede
xqe xq xs xaq
xde xd xs xad
xs
a)
d xad
xsr
Ud
xr
r
x ad
xsrd1
…
xrd1
rd1
xad
xsrdnd
xrdnd
xad
rdnd
xs
б)
q xaq
xsrq1
Uq
xrq1
xaq
…
rq1
xsrqnq
xrqnq
xaq
rdnq
53
54. Замещение синхронной машины источником ЭДС
При переходе к упрощенным статорным уравнениям вращающихся машинвозникает проблема симметризации источника ЭДС, замещающего генератор,
так как несимметричный по осям d и q источник ЭДС нельзя непосредственно
использовать в расчете мгновенного электрического режима схемы.
x
xd xq
2
E e U r jx I
Имеется возможность сохранить несимметрию генератора по продольной
и поперечной осям и не искажать демпферную систему генератора, если в
расчете мгновенного электрического режима схемы представить генератор
ЭДС за реактивностью рассеяния статора.
54
55. Замещение синхронной машины источником ЭДС
Из упрощённых статорных уравнений генератора (пренебрегли толькотрансформаторными ЭДС), в которые подставлены выражения для
потокосцеплений статорных контуров, можно выразить
1 s E q U q 1 s xs I d rI q
1 s E d U d 1 s xs I q rI d
Следовательно, при расчёте мгновенного электрического режима генератор
можно рассматривать как источник ЭДС
U Z s I
E
1 s
E q
E d
Eqe
1 s
Z s r jx s 1 s
I d
xad
Ede
I q
xaq
1 s
55
56. Упрощенные уравнения синхронного генератора
5657. Начальные условия
После расчёта исходного установившегося режима известны токгенератора и напряжение в узле включения генератора, определено
положение векторов напряжения узла и тока генератора на комплексной
плоскости.
Заданное скольжение sv общих осей dv, qv относительно синхронных
осей определяет частоту в энергосистеме в относительных единицах, при
которой сбалансирован исходный режим:
f 1 sv
Начальное значение скольжения ротора генератора относительно
синхронных осей в уравнении
s sv
Определение начальных значений остальных интегрируемых переменных
основано на построении векторной диаграммы генератора. Оси dv, qv, общие
для всех элементов схемы, совмещаются с осями комплексной плоскости.
57
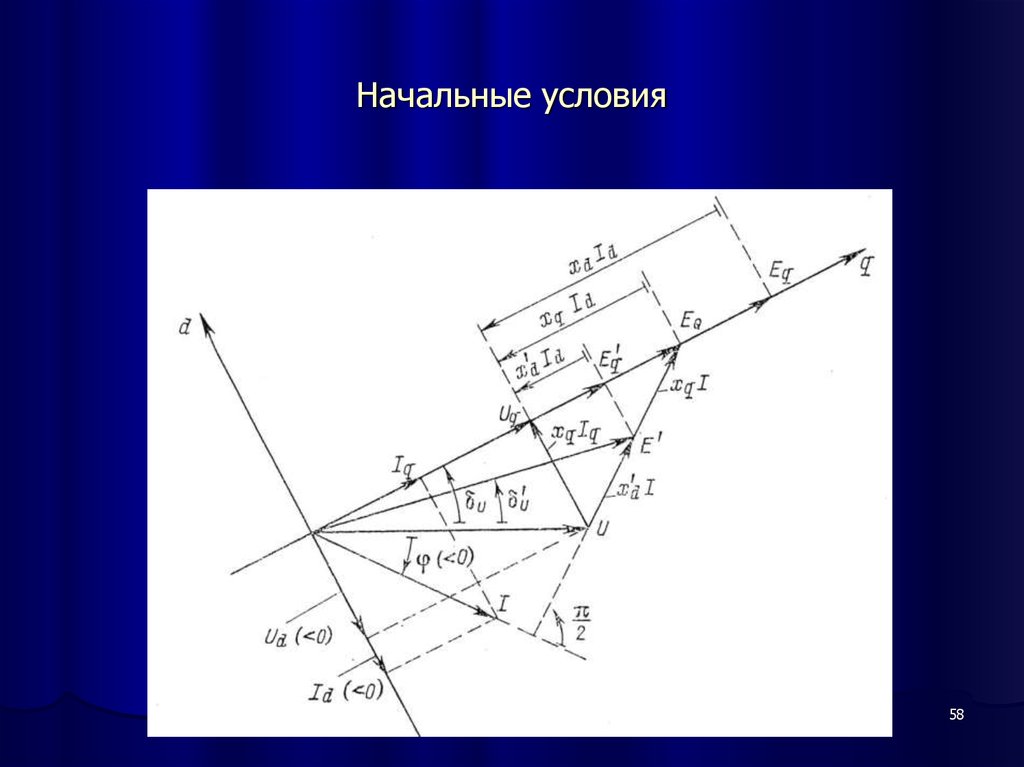
58. Начальные условия
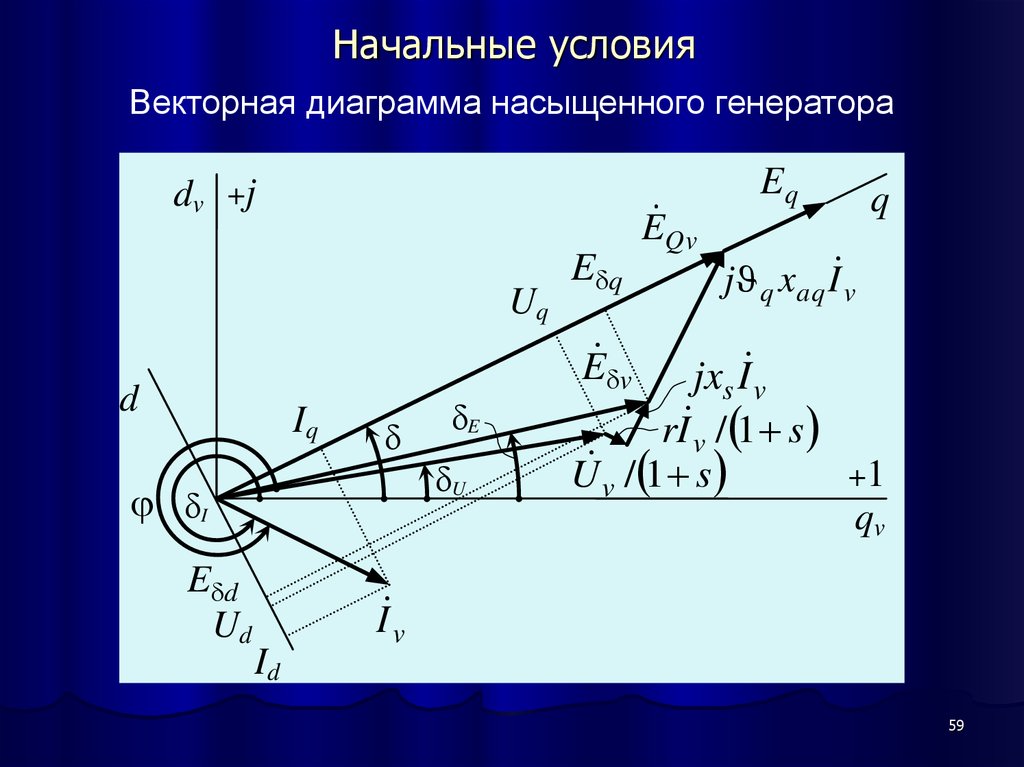
5859. Начальные условия
Векторная диаграмма насыщенного генератораd v +j
Uq
E q
E Qv
Eq
q
Ud
j q xaq I v
Ud
E v
d
Iq
δ
δU
δI
E d
UdUd
δE
jxs I v
Ud
rI v / 1 s
U v / 1 s
+1
qv
Id
I v
Ud
59
60. Начальные условия
1d q 1,0
U v Z q I v
E v E 2dv E 2qv
Z q r j 1 s xs q xaq
2
E Qv
3
U d U dv cos U qv sin
(1 s)
d q
U q U dv sin U qv cos
I d I dv cos I qv sin
I q I dv sin I qv cos
или определить углы
U qv Re U v
I qv Re I v
U arctg
U dv
U qv
EQdv
Im E Qv
arctg
arctg
Re EQv
EQqv
U dv Im U v
I dv Im I v
I arctg
I dv
I qv
и спроецировать концы векторов напряжения и тока на
собственные оси машины
U d U sin U
I d I sin I
U q U cos U
I q I cos I
60
61. Начальные условия
4E q
U q rI q
(1 s)
xs I d
E d
U d rI d
xs I q
(1 s)
или определить угол E arctg
E dv
E qv
и спроецировать конец вектора E v на собственные оси
E q E cos E
E d E sin E
5
Если генератор явнополюсный и насыщение стали учитывается
только в продольной оси, пересчитать параметр насыщения
d f ( E q )
61
62. Начальные условия
6Eq
E q
xad I d
d
Er Eq
7
r
xad
x
E q sr Eq
xr
xr
rdi
xad
E q
xrdi
rqk
8
xaq
xrqk
E d
M e d iq q id E q iq E d id
Mт Me
62
63. Математическая модель комплексной нагрузки
Комплексная нагрузка в общем содержит следующие составляющие:статическая (шунт, P и Q const, СХН)
kсн kад kсд 1,0
динамическая (АД и СД)
1 способ. Разбивают на составляющие текущую нагрузку узла,
которая получается в результате балансирования исходного
установившегося режима Pнг 0 jQнг 0
Полученная расчетом активная мощность нагрузки делится на
составляющие в соответствии с их долями.
Баланс реактивной мощности комплексной нагрузки узла в исходном
режиме замыкается коррекцией реактивной мощности статической
составляющей нагрузки
Qсн Qнг 0 Qад Qсд
2 способ. Разбивается на составляющие заданная нагрузка узла
Pнг jQнг
После расчета установившегося режима
Pнг 0 Рсн Рад Рсд Qнг 0 Qсн Qад Qад
63
64. Математическая модель комплексной нагрузки
Если комплексная нагрузка включена в узлы напряжением 35 кВи выше, потери в сети между узлом расчетной схемы и
действительным узлом подключения нагрузки включаются в
мощность нагрузки, а сама сеть исключается.
В задачах динамики это может быть неприемлемо, поскольку не
учитывается влияние сети на уровень напряжения на выводах
двигателей, что заведомо искажает характер переходного процесса.
Возникает задача учета влияния сети (линий, трансформаторов)
между узлом расчетной схемы и действительным узлом
подключения нагрузки.
64
65. Математическая модель комплексной нагрузки
a)б)
в)
Pнг Pс j Qнг Qс
Сеть СН
Pнг jQнг
Cхемы а и в
эквивалентны, если
в установившемся
режиме ток нагрузки
в схеме а равен току
трансформатора в
схеме в.
Сеть нагрузки
Pнг jQнг
Результирующий коэффициент трансформации можно назначить из условия, что
нормально допустимые отклонения напряжения на нагрузке в максимальном и
минимальном режимах равны ±5 %, а предельно допустимые отклонения не должны
превышать ±10 %.
Активное сопротивления ветви можно оценить по среднестатистическим
значениям потерь активной мощности в сети, а индуктивное – на основе соотношения
r/x сетей разных классов напряжения.
Полученные параметры затем проверяются и уточняются по результатам расчета
установившегося режима.
65
66. Моделирование СН, АД, СД
Статическая нагрузка моделируется или шунтом, или СХН.Динамическая нагрузка в узлах энергосистем замещается
эквивалентными АД и СД, описываемыми упрощенными
уравнениями Парка-Горева. Требования к моделям двигателей
определяются характером решаемых задач.
В задачах расчета электромеханических переходных процессов
в узлах нагрузки для получения достоверных результатов
необходимо индивидуальное моделирование агрегатов двигательмеханизм.
При индивидуальном моделировании к моделям двигателей
предъявляются следующие требования:
воспроизведение зависимостей тока и электромагнитного момента
различных типов двигателей в широком диапазоне изменения
скольжения ротора от пускового до рабочего или входного скольжения
(воспроизведение пусковых характеристик двигателей);
воспроизведение переходов двигателей из двигательного в
генераторный режим и обратно при коротких замыканиях в сети и при
перерывах питания в процессе группового выбега с последующим
переходом к индивидуальному выбегу.
66
67. Модель асинхронных двигателей
Классические уравнения Парка-Горева с однимэквивалентным контуром в каждой из осей d и q с
параметрами, не зависящими от режима машины, не
пригодны для моделирования АД, поскольку пусковые
характеристики двигателей формируются именно за
счет изменения параметров при изменении скольжения
ротора. Необходима доработка модели, чтобы
удовлетворить требования, предъявляемые к модели
АД для решения практических задач.
В практике моделирования для воспроизведения
пусковых характеристик двигателей ротор замещается
либо многоконтурной схемой с постоянными
параметрами контуров, либо одним контуром в каждой
оси d и q с переменными параметрами.
67
68. Рекомендации по учету нагрузки в расчетах
6869. Модель АД с многоконтурной схемой замещения ротора с постоянными параметрами роторных контуров
Асинхронный двигатель не имеет обмотки возбуждения исимметричен по осям d и q, поэтому d, q оси можно ориентировать
произвольно, исходя из удобства построения алгоритма.
Для АД справедливы следующие соотношения:
M ad M aq M a
Ld Lq L Ls M a
Lrdi Lrqi Lri Lsri M a
rrdi rrqi rri
d q
xad xaq xa
x d xq x x s xa
xrdi xrqi xri xsri xa nd nq n
Trdi Trqi Tri
Lri
x
1
ri
rri s rri s ri
69
70. Модель АД с многоконтурной схемой замещения ротора с постоянными параметрами роторных контуров
Система уравнений в собственных d, q осях, описывающаяасинхронный двигатель, приобретает вид
1 d d
1 s q riq u d
s dt
1 s d
1 d q
riq u q
s dt
d rdi
1
Erqi
dt
Tri
d rqi
dt
1
Erdi
Tri
ds 1
M мх M e
dt TJ
d
s s sv
dt
d xs id E q
q xs iq E d
rdi
xa
x
E q sri Erqi
xri
xri
rqi
i = 1,2,…,n
E q
E d
xa
x
E d sri Erdi
xri
xri
xa id
n
i 1
xa iq
E rqi
n
i 1
E rdi
i = 1,2,…,n
f E
E E 2q E 2d
M e d iq qid E qiq E d id
70
71. Модель АД с переменными параметрами
В модели двигателя с переменными параметрами и замещениемреальной системы роторных контуров двумя эквивалентными
контурами, по одному в оси d и q, воспроизведение пусковых
характеристик можно обеспечить, изменяя непосредственно
параметры модели, зависящие от режима машины, либо, по
аналогии с учетом насыщения генератора, можно ввести в
уравнения специальные переменные параметры, учитывающие
зависимость параметров идеализированной машины от ее режима.
Второй способ позволяет построить модель, для расчета
параметров которой можно разработать алгоритм, использующий
только каталожную информацию о двигателе.
71
72. Модель АД с переменными параметрами
Исходные уравнения асинхронного двигателя в именованныхединицах в собственных d, q осях можно записать в виде:
d
L id M aird L iq M airq rid ud ,
dt
d
L id M a ird L iq M a irq riq uq ,
dt
d 3
M a id Lr ird rr ird 0,
dt 2
d 3
M a iq Lr irq rr irq 0,
dt 2
J
d
M мх M e .
dt
L Ls M a
Lr Lsr M a
72
73. Модель АД с переменными параметрами
Введем в уравнения машины переменные параметры,учитывающие насыщение стали по пути магнитных потоков
рассеяния и взаимной индукции и распределение тока в стержнях
обмотки ротора:
M a xa
i, ir ,
M a xa
Ls xs
i,
Ls xs
Lsr xsr
ir , , f ir
Lsr xsr
rr rr f ir
Параметры M a , xa, Ls, xs , Lsr , xsr , r являются постоянными, не зависят
от электромагнитного состояния двигателя и определяются для
идеализированной машины.
73
74. Модель АД с переменными параметрами
Насыщенные коэффициенты само- и взаимоиндукции машинысвязаны с постоянными коэффициентами идеализированной
машины
M a M a ,
Lr Lsr M a
L Ls M a
Поэтому исходную систему уравнений можно переписать в виде:
d
dt
Ls M a id M aird Ls M a iq M airq rid ud
Ls M a id M a ird
d
Ls M a iq M airq riq uq
dt
d 3
M a id Lsr M a ird rr ird 0
dt 2
s M a
Lr
d 3
M aiq Lsr M a irq rr irq 0
dt 2
Erq s M a ird
J
d
M мх M e
dt
Erd s M airq
введём в уравнение
движения s
r
rr
r f ir
xr
приведем уравнения к относительным единицам А.А. Горева
74
75. Модель АД с переменными параметрами
xa2x xa
x
x
id sr
Erq a E q sr Erq
xr
xr
xr
xr
1 d d
(1 s) q rid u d
s dt
rd
1 d q
(1 s) d
riq u q
s dt
xa2
x xa
x
x
rq
iq sr
Erd a E d sr Erd
xr
xr
xr
xr
d rd
s r Erq
dt
d rq
dt
s r E rd
ds
1
M мх M e
dt TJ
d
s s sv
dt
d xs xa id Erq xsid E q
q xs xa iq Erd xsiq E d
E q xaid Erq
M e d iq qid E qiq E d id Erqiq Erd id
E d xaiq Erd
E E 2q E 2d
2
2
Er Erq
Erd
i, E
Er , E , s su
r r s su
i, Er , E
f ir s su
75
76. Модель АД с переменными параметрами
Эту модель можно упростить без ущерба для ее точности.В диапазоне скольжений sкр s sкр , где sкр – критическое
скольжение, параметры машины можно считать постоянными.
Для формирования пусковых характеристик достаточно
учитывать изменение параметров в диапазоне скольжений от
пускового до критического.
Состояние стали зубцовых слоев статора и ротора с одной
стороны и стали массива ротора и спинки статора с другой стороны,
по которым проходит магнитный поток взаимной индукции, в
процессе пуска и при переходе от пускового к рабочему режиму
изменяется во взаимно противоположных направлениях. Это
позволяет принять допущение о постоянстве параметра насыщения
по пути магнитного потока взаимной индукции . Кроме того,
пусковые характеристики машины от значения этого параметра
практически не зависят, поэтому для всех типов двигателей
допустимо принимать одно и то же среднее значение н .
76
77. Модель АД с переменными параметрами
Глубокое насыщение стали зубцовых слоев статора и роторапроисходит за счет увеличения токов обмоток статора и ротора,
поэтому в диапазоне скольжений от пускового до критического
можно пренебречь весьма слабой зависимостью параметров и
от магнитного потока взаимной индукции, полагая, что
i
Er , s su
Принятые допущения позволяют исключить из модели двигателя
функциональную зависимость i, Er , E , уравнения для
определения E q , E d и упростить зависимости переменных
параметров и от режима машины.
77
78. Модель АД с переменными параметрами
Переход к форме записи уравнений с использованиемкоэффициентов магнитной связи и рассеяния контуров статора и
ротора позволяет еще больше упростить запись уравнений
двигателя.
Коэффициенты магнитной связи и рассеяния для идеализированной
машины:
x
s s
x
sr
xsr
xr
x
s 1 s a
x
sr 1 sr
xa
xr
xs s x
xa s x
xa2
s sr
xxr
xsr sr xr
xa sr xr
1
Уравнения для потокосцеплений
контуров статора и ротора
принимают вид
d s s xid Erq
q s s xiq Erd
rd xid sr sr Erq
rq xiq sr sr Erd
Параметры насыщения
s s s s i
sr sr sr sr Er , s su
Пусковые характеристики формируются
r r s su
s i
sr Er , s su
78
79. Модель АД с переменными параметрами
АД с короткозамкнутым ротором в собственных d, q осяхописывается следующей системой уравнений:
1 d d
(1 s) q rid u d
s dt
1 d q
(1 s ) d
riq u q
s dt
d rd
s r Erq
dt
d rq
dt
s r E rd
ds 1
M мх M e
dt TJ
d
s s sv
dt
d s xid Erq
q s xiq Erd
rd xid sr Erq
rq xiq sr Erd
M e d iq qid Erqiq Erd id
s s i
sr sr Er , s su
2
2
Er Erq
Erd
r r s su
н const
79
80. Модель АД с переменными параметрами
Уравнения симметричных по осям d и q асинхронных машинцелесообразно записывать не в собственных, а в общих dv, qv осях.
ud udv cos uqv sin
uq udv sin uqv cos
id idv cos iqv sin
iq idv sin iqv cos
d dv cos qv sin
q dv sin qv cos
rd rdv cos rqv sin
rq rdv sin rqv cos
Erd Erdv cos Erqv sin
Erq Erdv sin Erqv cos
Подставим выражения для
d q
id iq
u d uq
в статорные уравнения АД. После дифференцирования и
преобразований получим
80
81. Модель АД с переменными параметрами
1s
d qv
d dv
1 sv dv sin qv cos r idv cos iqv sin udv cos uqv sin
cos
sin
dt
dt
1 sv dv cos qv sin
1
s
d qv
d dv
r idv sin iqv cos udv sin uqv cos
sin
cos
dt
dt
Умножая первое уравнение на cos δ, второе – на sin δ, и вычитая из первого
уравнения второе, умножая первое уравнение на sin δ, второе – на cos δ и
складывая, получим уравнения для статора двигателя в общих осях:
1 d dv
(1 sv ) qv ridv u dv
s dt
(1 sv ) dv
1 d qv
riqv u qv
s dt
Аналогично преобразуются уравнения для пары для роторных контуров
d rdv
s r Erqv s s sv rqv
dt
d rqv
dt
s r Erdv s s sv rdv
Аналогично преобразуются пары алгебраических уравнений
для потокосцеплений.
81
82. Модель АД с переменными параметрами
Уравнения статора двигателя целесообразно объединить с уравнениямилинии питания, которой он подключен к узлу, общему для нескольких
двигателей, чтобы уменьшить число узлов в расчетной схеме.
U v
I v
U 1v
Z к rк jx к
1 d dv
(1 sv ) qv rк idv udv u1dv
s dt
Zк
1 d qv
(1 sv ) dv
rк iqv uqv u1qv
s dt
M
где
Статорные уравнения
принимают вид
где
dv xк idv
qv xкiqv
1 d dv
1 sv qv r rк idv udv
s dt
1 sv dv
1 d qv
r rк iqv uqv
s dt
dv s x xк idv Erqv
qv s x xк iqv Erdv
82
83. Модель АД с переменными параметрами
Модель АД с переменными параметрами в общих dv, qv осях1 d dv
1 sv qv r rк idv udv
s dt
1 sv dv
1 d qv
r rк iqv uqv
s dt
dv s x xк idv Erqv
qv s x xк iqv Erdv
rdv xidv sr Erqv
rqv xiqv sr Erdv
d rdv
s r Erqv s s sv rqv
dt
s s iv
d rqv
2
2
sr sr Erv , s su Erv Erqv Erdv
dt
s r Erdv s s sv rdv
ds 1
M мх M е
dt TJ
r r s su
н
M e dviqv qvidv Erqviqv Erdvidv
83
84. Модель АД с переменными параметрами
Учет и рассеивание потерь в асинхронном двигателеПри индивидуальном моделировании асинхронных двигателей
возникает задача учета и рассеивания потерь в двигателях для
формирования адекватных внешних характеристик двигателя со
стороны сети и со стороны вала.
U v
I v
U 1v
н 80 96 %
Sн
Zк
M
Iн
Pн
cos н н
Sн
3U н
Модель двигателя с переменными параметрами обеспечивает учет и
рассеивание потерь в двигателе при пуске и самозапуске в диапазоне
скольжений от пускового до критического за счет изменения параметров.
Кратность пускового тока определяется по отношению к номинальному
току и содержит составляющую потерь. Если модель воспроизводит
пусковой ток двигателя, то в потребляемом из сети токе присутствует
составляющая потерь. Если при этом модель воспроизводит зависимость
момента на валу от скольжения, это означает, что модель рассеивает
84
потери в двигателе.
85. Учет и рассеивание потерь в асинхронном двигателе
В диапазоне рабочих скольжений модель двигателя на основеуравнений Парка-Горева не рассеивает потери в стали статора,
механические, добавочные потери, а также потери в активном
сопротивлении обмотки статора, если полагают активное
сопротивление равным нулю. Это искажает внешние
характеристики модели двигателя со стороны сети или со стороны
вала.
Если параметры модели определены так, чтобы в номинальном
режиме из сети потреблялась номинальная мощность и ток
двигателя был равен номинальному, то это приведет к завышению
момента на валу, скольжение ротора будет меньше номинального.
Если параметры модели определены так, чтобы в номинальном
режиме на валу получался номинальный момент, то потребляемый
из сети ток будет меньше номинального, а это приведет к
погрешностям в определении напряжения в узлах схемы.
Эти погрешности проявляются не только в рабочем режиме, они
могут исказить результаты расчетов электромеханических
переходных процессов.
85
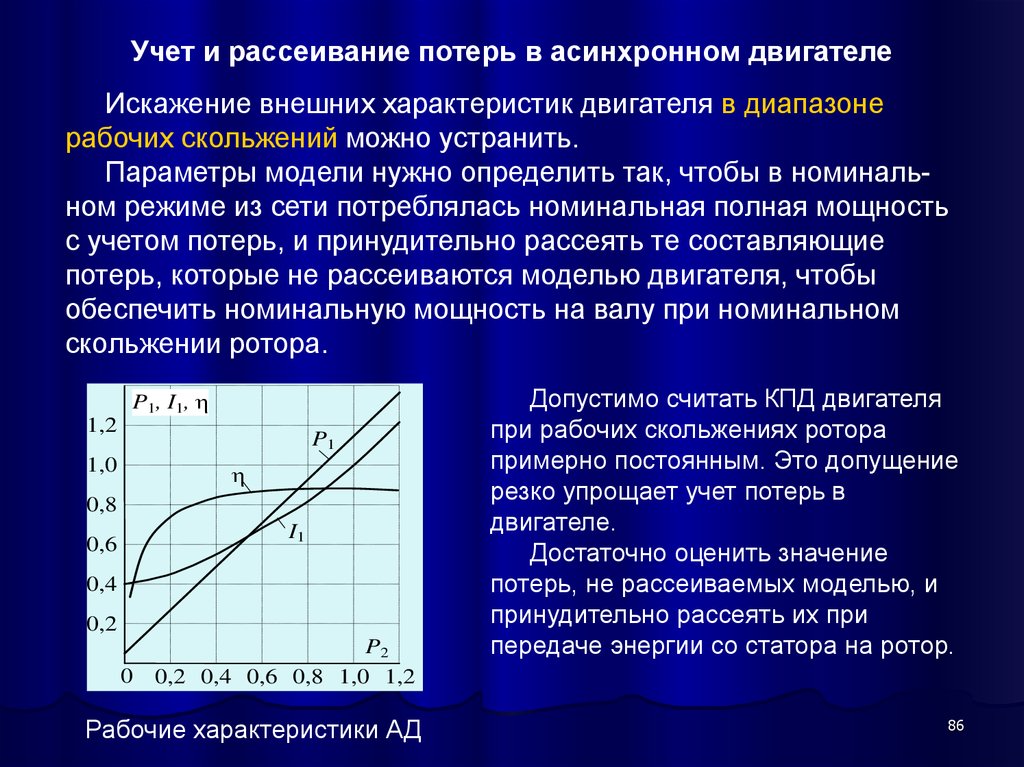
86. Учет и рассеивание потерь в асинхронном двигателе
Искажение внешних характеристик двигателя в диапазонерабочих скольжений можно устранить.
Параметры модели нужно определить так, чтобы в номинальном режиме из сети потреблялась номинальная полная мощность
с учетом потерь, и принудительно рассеять те составляющие
потерь, которые не рассеиваются моделью двигателя, чтобы
обеспечить номинальную мощность на валу при номинальном
скольжении ротора.
P1, I1, η
1,2
P1
1,0
η
0,8
I1
0,6
0,4
0,2
0
P2
0,2 0,4 0,6 0,8 1,0 1,2
Рабочие характеристики АД
Допустимо считать КПД двигателя
при рабочих скольжениях ротора
примерно постоянным. Это допущение
резко упрощает учет потерь в
двигателе.
Достаточно оценить значение
потерь, не рассеиваемых моделью, и
принудительно рассеять их при
передаче энергии со статора на ротор.
86
87. Учет и рассеивание потерь в асинхронном двигателе
Энергетические диаграммы асинхронного двигателя (а)и его модели (б) в номинальном режиме
б)
а)
Р1н
Р1н
pм1
Рэм
pст
pм1
Рe=P1нηнs–рм1
Рмх
pм2
pст+рд+рмх
pд
Р2н
pмх
Р2н= Рмх
pм2
нs
P1н pст рмх рд - коэффициент полезного действия, учитывающий
Р1н
потери, не рассеиваемые моделью
н s
p м1
r1*(н )
н
н
1 sн Р1н 1 sн cos н
где r1*(н) r1[Ом]
Sн
U н2
н s
н
, если r = 0
1 sн
M e d iq q id н s Erq iq Erd id н s
87
88. Модель АД с переменными параметрами
Упрощенные уравнения асинхронного двигателя1 sv q r rк I d U d
1 sv d r rк I q U q
Асинхронный двигатель как источник ЭДС
E E q jE d U ZI
Eq U q I d X I q R
Ed U d I d R I q X
Eq
1 sv
rd
sr
Ed
1 sv
rq
sr
Z R jX
R r rк
X (1 sv ) s
sr
x xк
88
89. Модель АД с переменными параметрами
Статическая модель асинхронного двигателя(Самостоятельно )
89
90. Модель АД с переменными параметрами
Расчет параметров модели АД по каталожным данным(самостоятельно)
Удовлетворительные результаты в воспроизведении
пусковых характеристик различных типов двигателей дают
обобщенные функции αs, αsr и ρr вида
s b0
b1
I
sr sr 0 1 sr1 1 F ( s)
sr 0
r r 0 1 r1 1 F ( s)
r 0
где
F (s) a0 s su a1 a2 s su
90
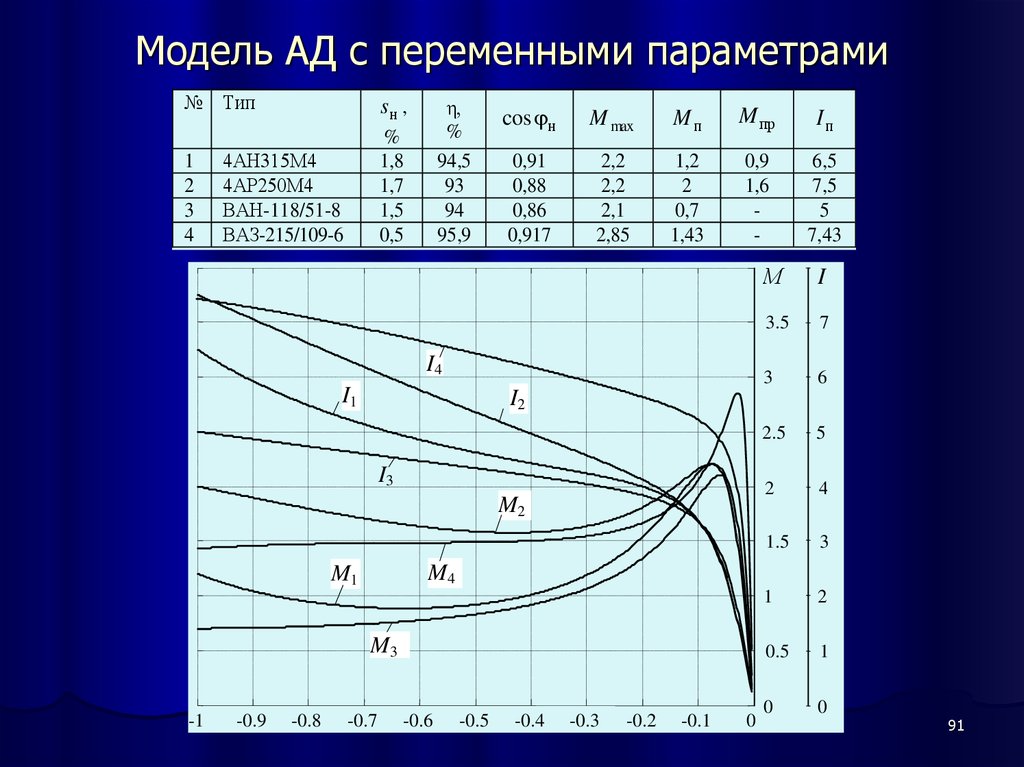
91. Модель АД с переменными параметрами
№ Тип1
2
3
4
η,
%
94,5
93
94
95,9
sн ,
%
1,8
1,7
1,5
0,5
4АН315М4
4АР250М4
ВАН-118/51-8
ВАЗ-215/109-6
cos н
M max
Mп
M пр
Iп
0,91
0,88
0,86
0,917
2,2
2,2
2,1
2,85
1,2
2
0,7
1,43
0,9
1,6
-
6,5
7,5
5
7,43
I4
I1
M2
M3
-0.8
3.5
7
3
6
2.5
5
2
4
1.5
3
1
2
0.5
1
0
0
M4
M1
-0.9
I
I2
I3
-1
М
-0.7
-0.6
-0.5
-0.4
-0.3
-0.2
-0.1
0
91
92. Модель АД с переменными параметрами
Расчёт начальных условий (самостоятельно)92
93. Моделирование синхронных двигателей
На практике для воспроизведения пусковых характеристик СДприменяют две модели – с многоконтурной схемой замещения
ротора (МКСЗР) с постоянными параметрами контуров и модель с
переменными параметрами.
Уравнения записывают в собственных d,q осях с
преобразованием переменных в общую систему координат при
расчете электрического режима схемы и обратно в собственную
систему координат при расчете режима двигателя.
Обычно МКСЗР применяется при индивидуальном
моделировании мощных уникальных двигателей, для которых
синтезированы параметры МКСЗР.
При отсутствии параметров многоконтурной схемы замещения
ротора можно использовать модель с переменными
параметрами. В частности, ее целесообразно применить для
эквивалентных синхронных двигателей комплексной нагрузки
узлов.
93
94. Модель СД с переменными параметрами
Модель синхронного двигателя с переменными параметрамиможно построить по аналогии с моделью асинхронного двигателя.
Но для синхронного двигателя нецелесообразно вводить в
уравнения специальные переменные параметры, учитывающие
зависимость реактивностей рассеяния контуров статора и
эквивалентных роторных контуров идеализированной машины от
ее режима.
Вследствие несимметрии машины по осям d и q не удается
существенно упростить запись уравнений. Поэтому лучше
изменять непосредственно сами параметры, зависящие от
режима машины.
94
95. Модель СД с переменными параметрами
Систему уравнений для СД с двумя эквивалентными роторнымиконтурами с переменными параметрами, замещающими пусковую
обмотку явнополюсного или бочку ротора неявнополюсного
двигателя, можно записать в виде
Изменение параметров:
1 d d
(1 s) q rid u d
s dt
(1 s ) d
1 d q
riq u q
s dt
d r
s r Er E q
dt
d rd
s rd Erq ,
dt
d rq
s rq Erd ,
dt
rrd rrd s su , xsrd xsrd s su ,
q xs iq E d ,
xrd xad xsrd ,
r
rd
rrq rrq s su , xsrq xsrq s su ,
xad
x
E q sr Eq ,
xr
xr
xrq xaq xsrq ,
xad
x
E q srd Erq ,
xrd
xrd
rq
xaq
xrq
E d
xsrq
xrq
Erq ,
E q d xad id Eq Erq
E d q xaq iq Erd
ds 1
M мх M е
dt TJ
d
s s sv
dt
d xs id E q ,
M e d iq q id E q iq E d id
НЯПСД d q f E
ЯПСД
d f E q q 1,0.
E E 2d E 2q .
rd
rrd
,
xrd
rq
rrq
r
xrq
.
rr
const ,
xr
d q 1,0 const
95
96. Статическая модель СД
Статическая модель с использованием комплексныхамплитуд переменных и расчёт параметров модели по
каталожным данным - самостоятельно
96
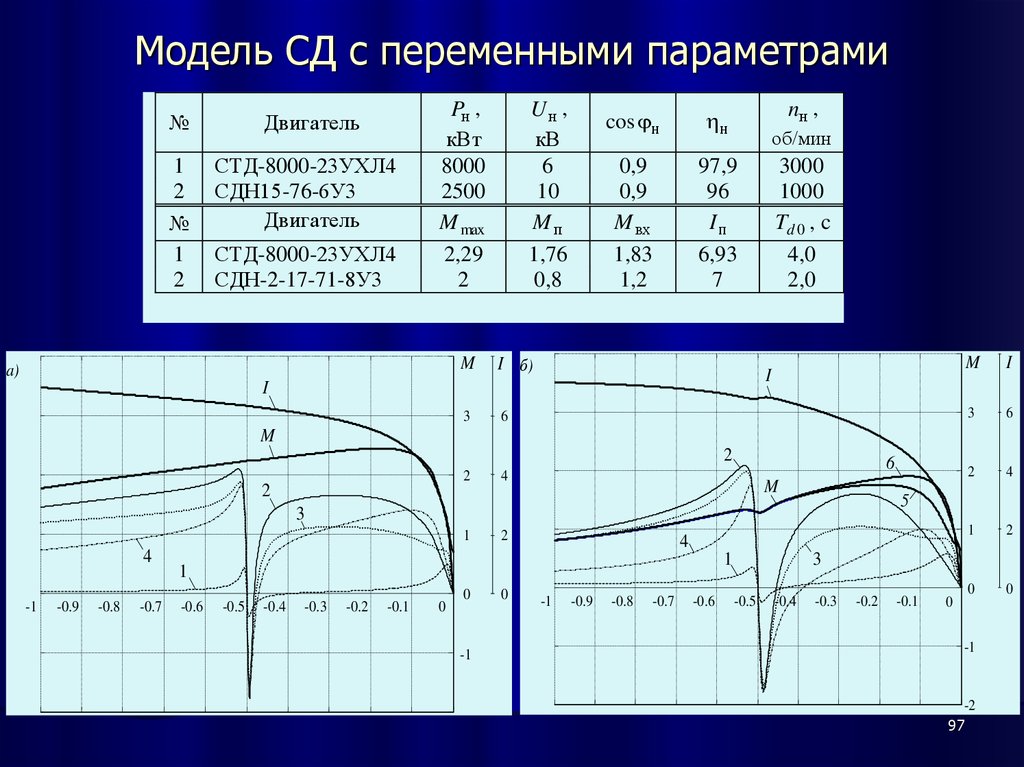
97. Модель СД с переменными параметрами
№Двигатель
1
2
№
1
2
СТД-8000-23УХЛ4
СДН15-76-6У3
Двигатель
СТД-8000-23УХЛ4
СДН-2-17-71-8У3
Pн ,
кВт
8000
2500
M max
2,29
2
a)
Uн ,
кВ
6
10
Mп
1,76
0,8
M
I б)
3
6
2
4
nн ,
cos н
н
0,9
0,9
M вх
1,83
1,2
97,9
96
Iп
6,93
7
об/мин
3000
1000
Td 0 , c
4,0
2,0
I
I
M
I
3
6
2
4
1
2
0
0
M
2
2
6
M
5
3
1
4
-1
-0.9
-0.8
-0.7
2
4
1
1
-0.6
-0.5
-0.4
-0.3
-0.2
-0.1
0
0
-1
0
-1
-0.9
-0.8
-0.7
-0.6
3
-0.5
-0.4
-0.3
-0.2
-0.1
0
-1
-2
97
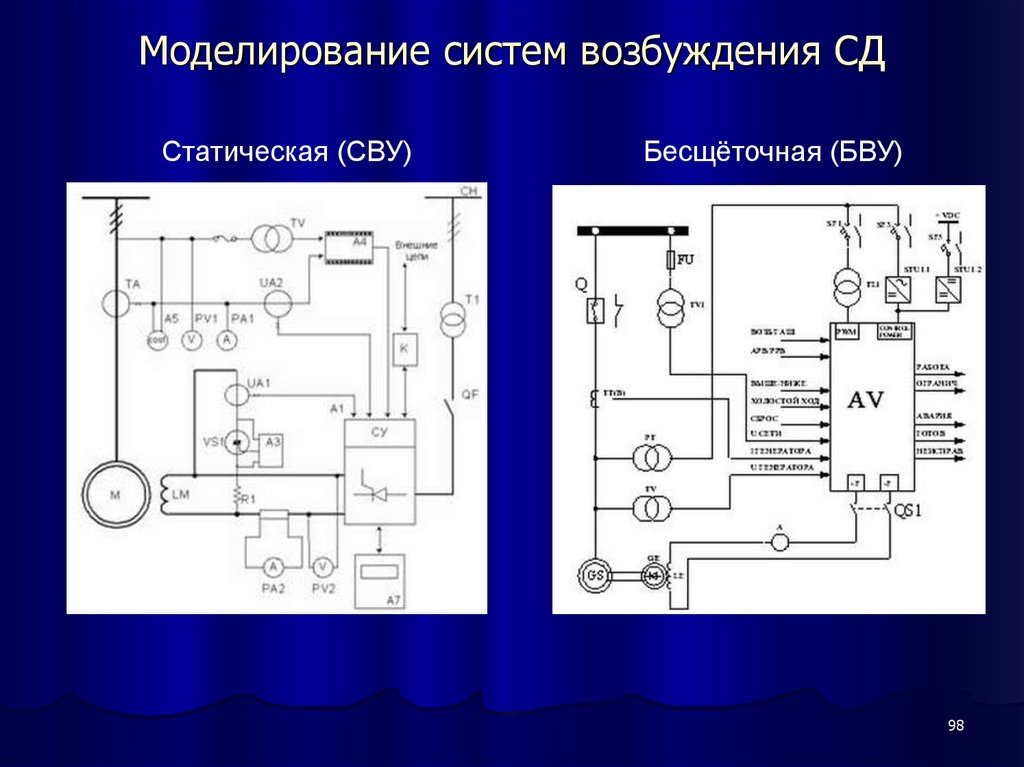
98. Моделирование систем возбуждения СД
Статическая (СВУ)Бесщёточная (БВУ)
98
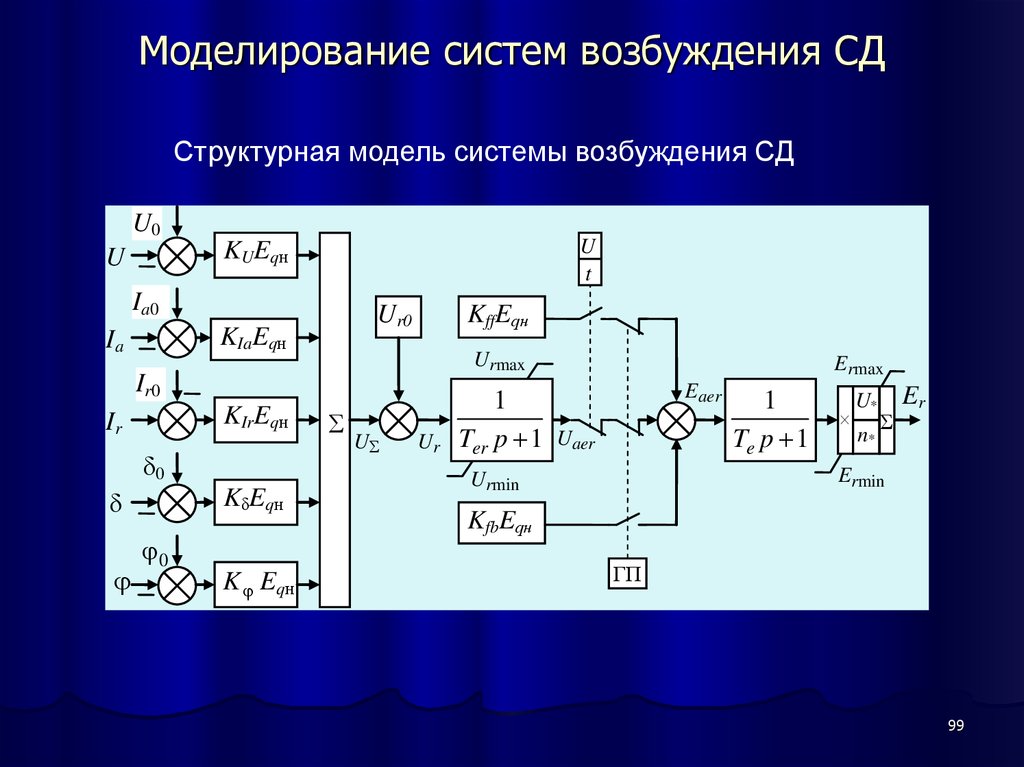
99. Моделирование систем возбуждения СД
Структурная модель системы возбуждения СДU0
U
t
KUEqн
U
Ia0
Ur0
KIaEqн
Ia
Urmax
Ir0
KIrEqн
Ir
δ0
KδEqн
δ
0
K Eqн
KffEqн
Σ
UΣ
Ermax
Eaer
1
Ur Ter p 1 Uaer
1
Te p 1
U*
n*
Σ
Er
Ermin
Urmin
KfbEqн
ГП
99
100. Рекомендации по учету нагрузки в расчетах
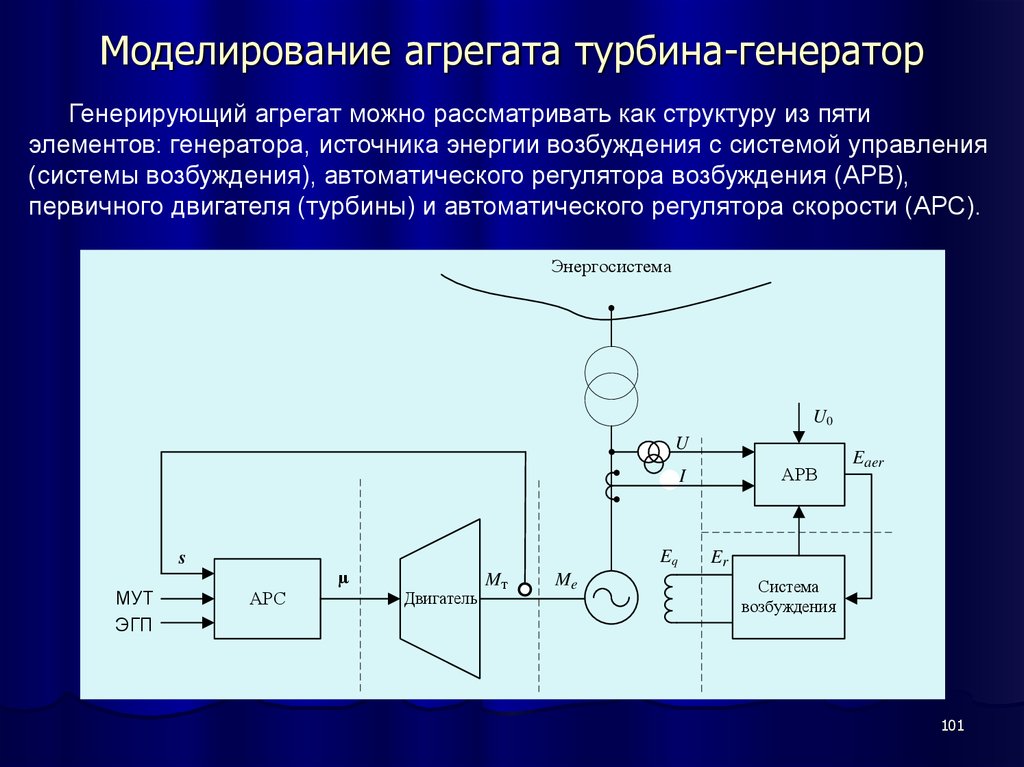
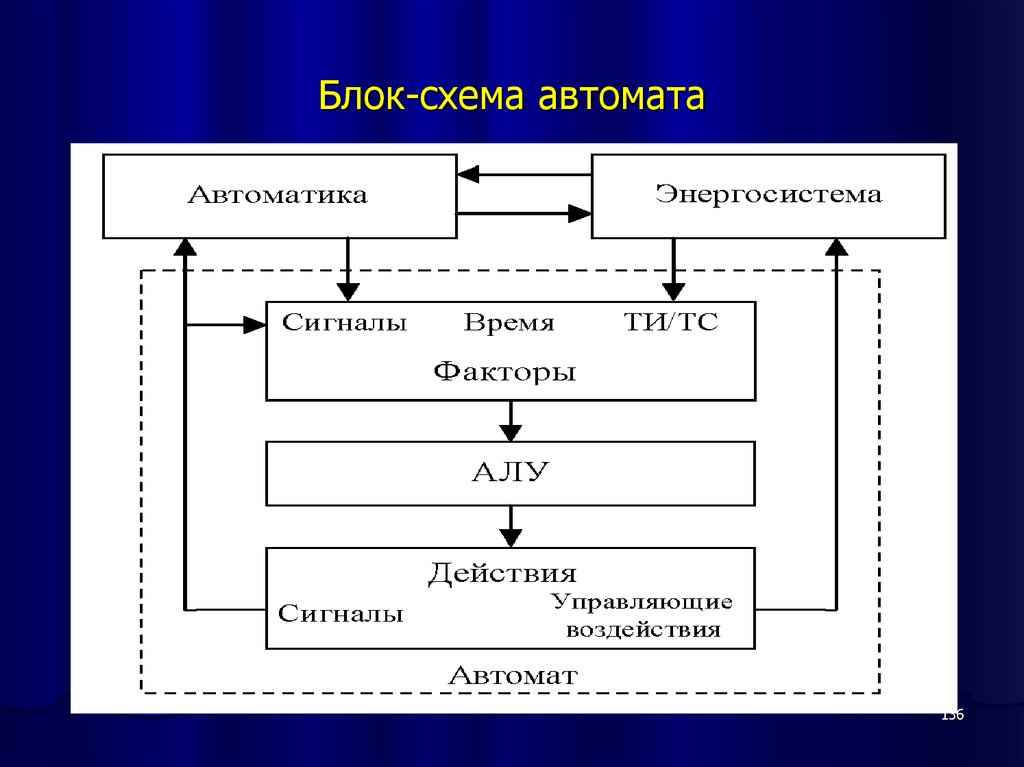
100101. Моделирование агрегата турбина-генератор
Генерирующий агрегат можно рассматривать как структуру из пятиэлементов: генератора, источника энергии возбуждения с системой управления
(системы возбуждения), автоматического регулятора возбуждения (АРВ),
первичного двигателя (турбины) и автоматического регулятора скорости (АРС).
Энергосистема
U0
U
АРВ
I
s
МУТ
ЭГП
Eq
µ
АРС
Двигатель
Mт
Me
Eaer
Er
Система
возбуждения
101
102. Моделирование агрегата турбина-генератор
При записи уравнений каждого из структурных элементов агрегатавозникают вопросы выбора единиц измерений величин,
фигурирующих в уравнениях, и согласования выходов и входов
структурных элементов.
Уравнения структурных элементов агрегата целесообразно
записывать в относительных единицах при номинальных условиях,
выбирая за базисные величины соответствующие номинальные
значения величин. Это упрощает запись уравнений и контроль
допустимого диапазона изменения величин, позволяет сравнивать
параметры различных типов элементов.
При «стыковке» моделей элементов агрегата входные и выходные
величины, фигурирующие в уравнениях, должны быть приведены к
одной системе единиц.
102
103. Моделирование агрегата турбина-генератор
Уравнения первичного двигателя и АРС рационально записыватьв относительных единицах, принимая за базисные количества
номинальные мощность и момент турбины (о.е.т.).
Тогда в установившемся режиме относительное перемещение
регулирующего органа первичного двигателя равно моменту
турбины в относительных единицах:
ds
1
M т M e
dt TJ
Mт
P
M т[ о.е.т. ]
т
M т.н Pт.н
2s
T J
J
Sб p 2
При подстановке момента первичного двигателя в уравнение
движения агрегата, где инерционная постоянная отнесена к ном.
полной мощности генератора и момент генератора Ме выражен в
долях номинального момента генератора, момент турбины тоже
нужно привести к относительным единицам генератора (о.е.г.) :
M т [о.е.г .]
M т [о.е.т. ] М т.н
M e.н
M т [ о.е.т ] Pт.н
S г.н
М т[о.е.т ] K пр
K пр
Рт.н
cos н
Рг.н
103
104. Моделирование агрегата турбина-генератор
При записи уравнений генератора в о.е. А.А. Горева ЭДС Eqгенератора, отнесенная к номинальному напряжению статора,
численно равна напряжению возбуждения Er, отнесенному к
базисному напряжению контура возбуждения СГ. Уравнения контура
возбуждения и системы возбуждения в относительных единицах
оказываются согласованными.
Коэффициенты передачи каналов регулирования АРВ принято
выражать в специальных единицах возбуждения холостого хода
(е.в.х.х.) или единицах возбуждения номинальных (е.в.н.) на
единицу регулируемого параметра режима.
Для приведения коэффициентов передачи к е.в.х.х. за базисные
значения тока и напряжения возбуждения принимаются их значения
при номинальном напряжении на выводах статора на холостом ходе
машины с номинальной угловой скоростью.
Следовательно, при использовании системы о.е. А.А. Горева
базисные величины контура возбуждения совпадают с базисными
величинами для АРВ и системы возбуждения. Входные и выходные
величины в уравнениях системы возбуждения и АРВ являются
104
согласованными.
105. Моделирование агрегата турбина-генератор
При записи уравнений АРВ чаще используют е.в.н. За базисноезначение тока и напряжения возбуждения принимаются их значения
при номинальном напряжении на выводах статора, номинальной
мощности и номинальной угловой скорости машины.
Следовательно, отношение этих специальных о.е. равно:
е.в.н.
Er н[е.в.х.х. ] Eq н[е.н.с.]
е.в.х.х.
Для согласования уравнений АРВ и системы возбуждения
необходимо выход каналов АРВ, выраженный в е.в.н., пересчитать в
е.в.х.х. Для этого достаточно коэффициенты передачи каналов АРВ
умножить на Eq н .
105
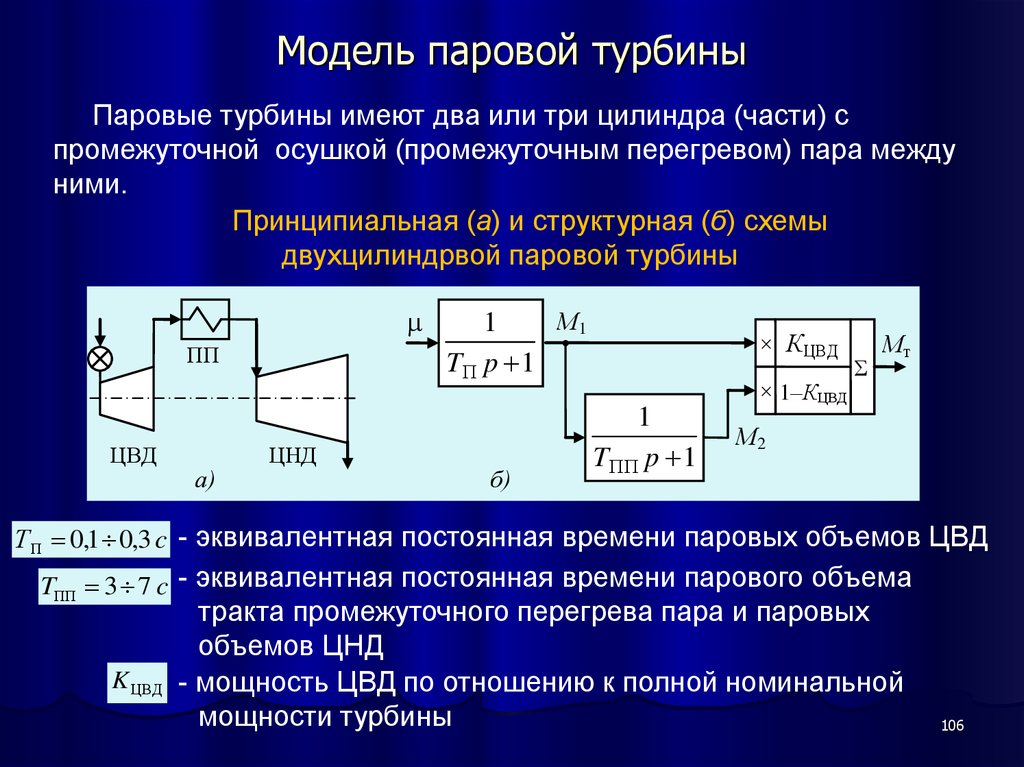
106. Модель паровой турбины
Паровые турбины имеют два или три цилиндра (части) спромежуточной осушкой (промежуточным перегревом) пара между
ними.
Принципиальная (а) и структурная (б) схемы
двухцилиндрвой паровой турбины
ПП
ЦВД
а)
ЦНД
М1
1
TП p 1
б)
КЦВД
1–КЦВД
1
TПП p 1
Σ
Мт
М2
Т П 0,1 0,3 c - эквивалентная постоянная времени паровых объемов ЦВД
TПП 3 7 c - эквивалентная постоянная времени парового объема
K ЦВД
тракта промежуточного перегрева пара и паровых
объемов ЦНД
- мощность ЦВД по отношению к полной номинальной
мощности турбины
106
107. Модель паровой турбины
Структурной схеме соответствует следующая система уравнений:dM 1 1
M1
dt
TП
dM 2
1
M1 M 2
dt
TПП
M т K ЦВД M 1 1 K ЦВД M 2
Начальные условия определяются по балансу моментов турбины
и генератора на валу агрегата в исходном установившемся режиме
M1 M 2 M т
Me
K пр
Mт
107
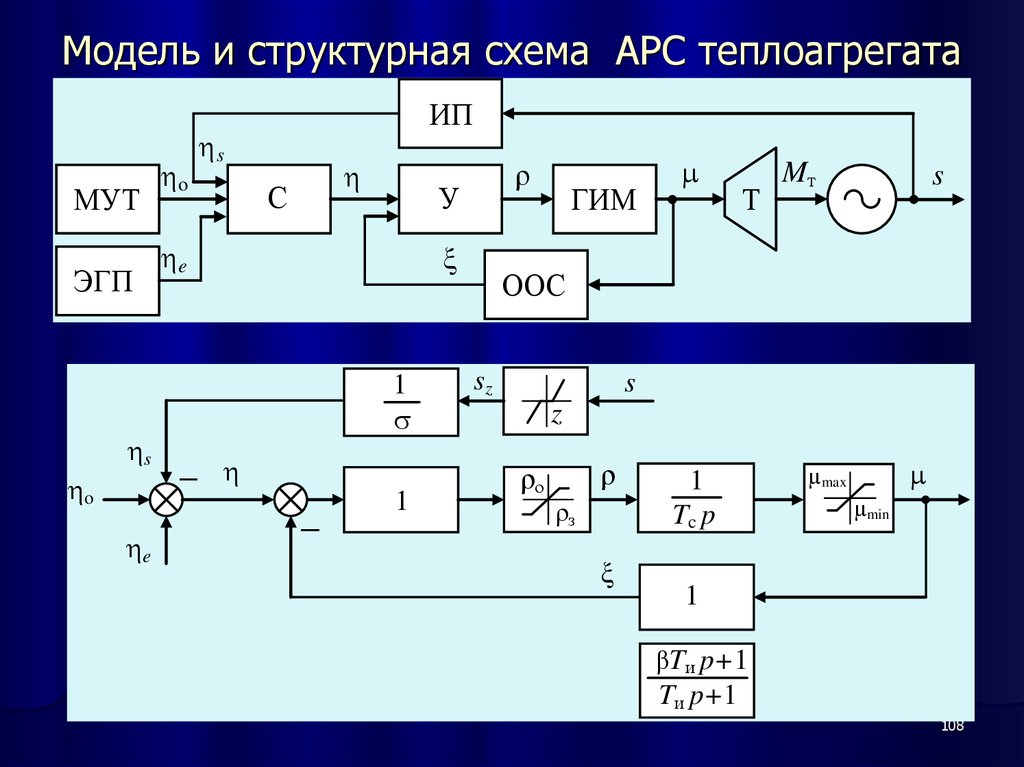
108. Модель и структурная схема АРС теплоагрегата
МУТЭГП
s
o
e
o
ИП
s
С
ρ
У
e
1
–
–
1
ГИМ
Т
Mт
s
ООС
sz
s
z
ρ
ρо
ρз
ξ
1
Tc p
µmax
µmax µmin
1
βTи p+1
Tи p+1
108
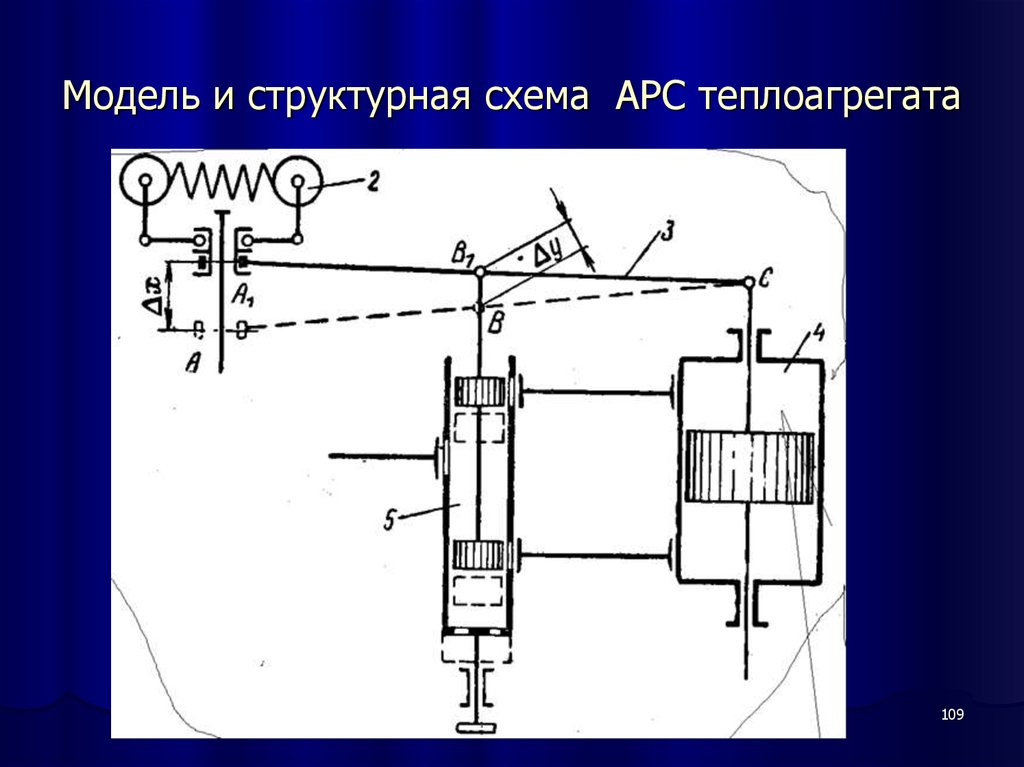
109. Модель и структурная схема АРС теплоагрегата
109110. Модель и структурная схема АРС теплоагрегата
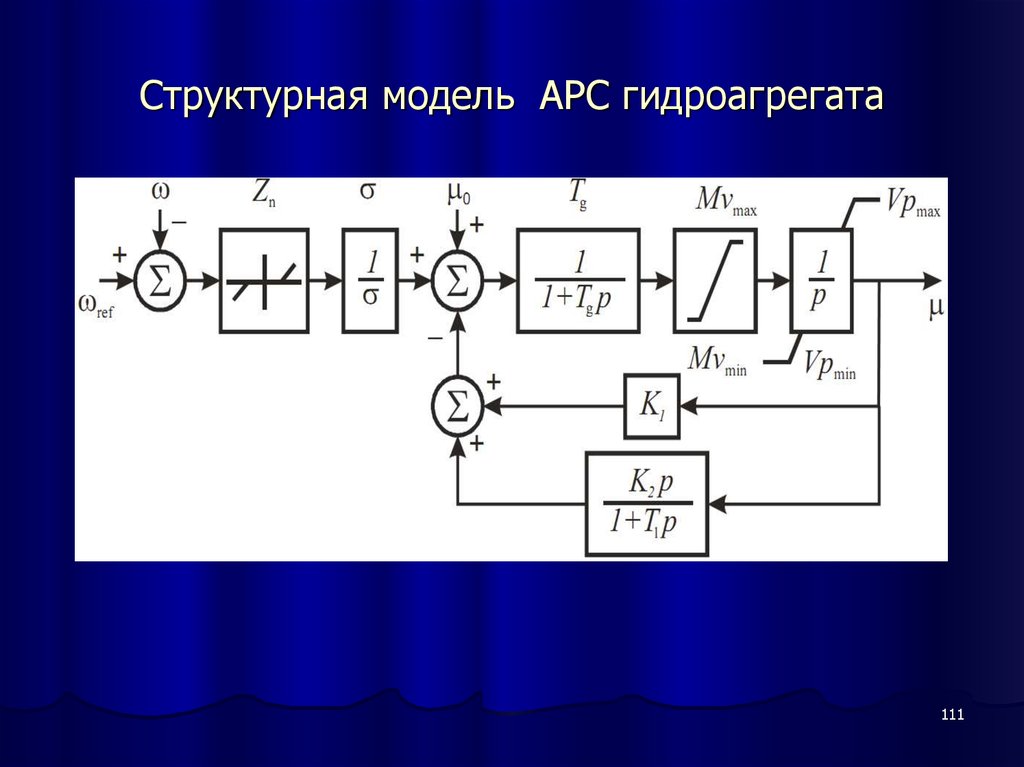
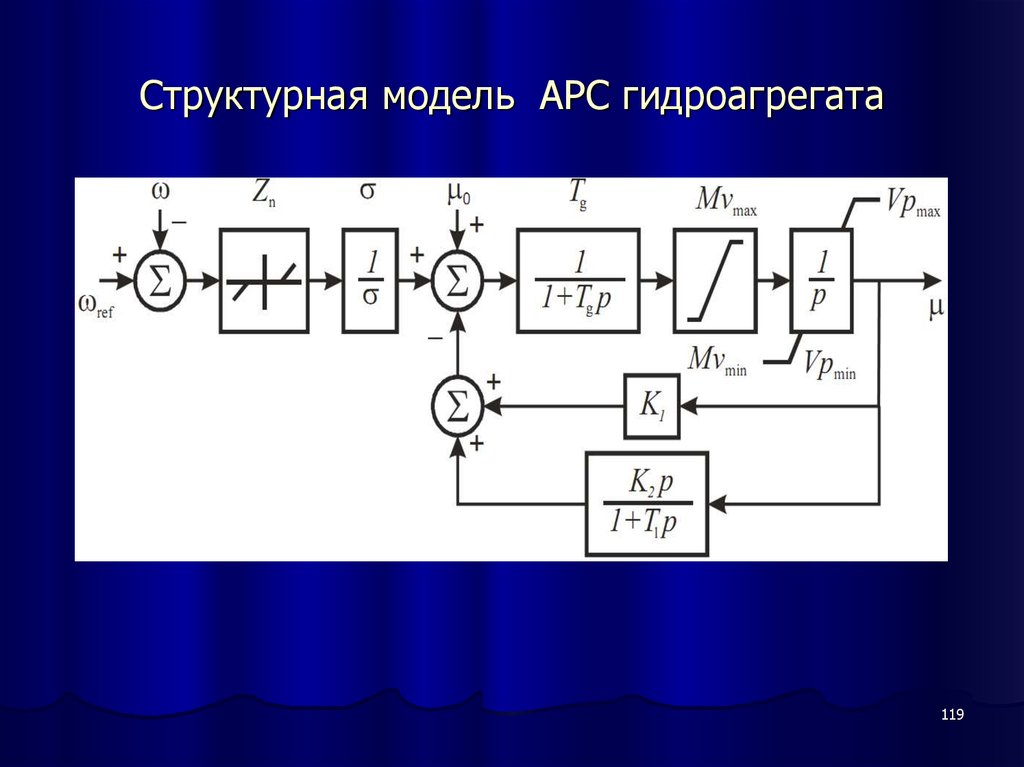
110111. Структурная модель АРС гидроагрегата
111112. Модель гидравлической турбины
W ( p)M т ( p ) Tw p 1
Tw
( p )
p 1
2
1
dM т
d
2 M т
dt
T
dt
w
Me
Mт
K пр
Tw
-
Mт
время изменения скорости воды в водоводе
от нуля до номинальной, с
112
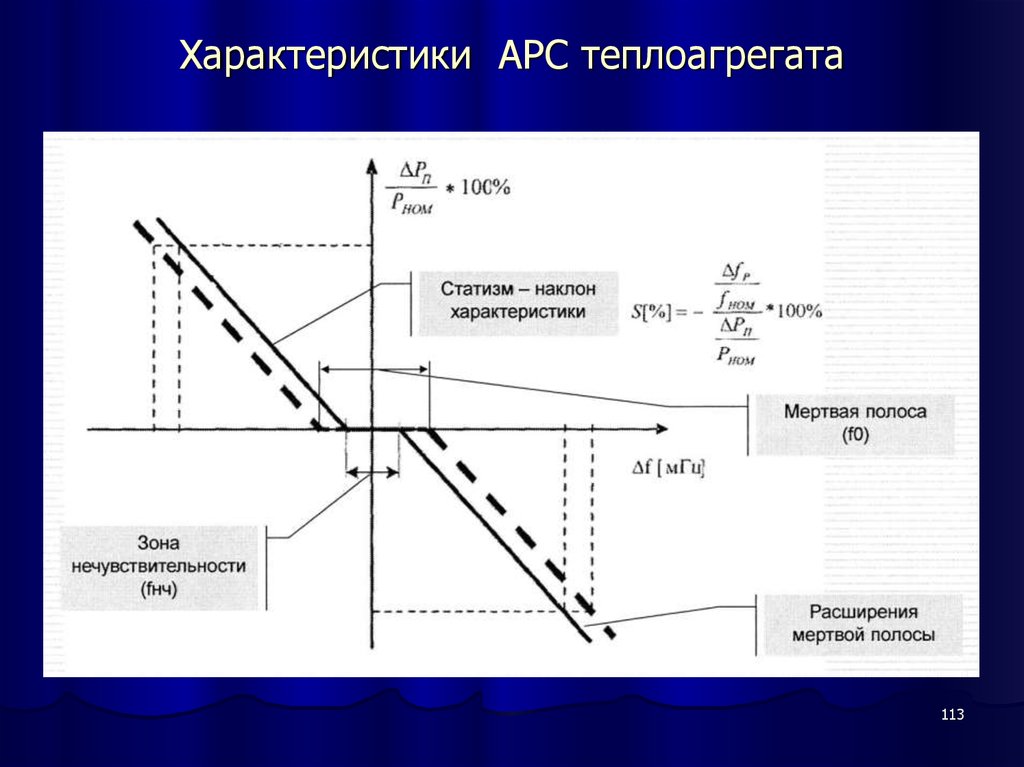
113. Характеристики АРС теплоагрегата
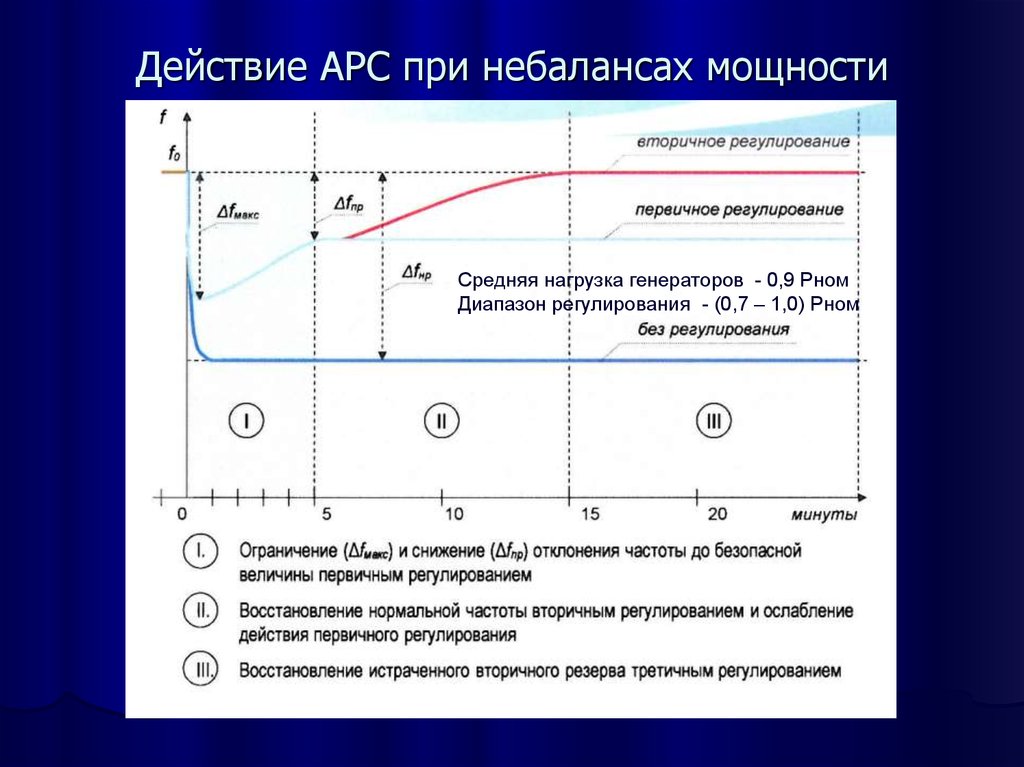
113114. Действие АРС при небалансах мощности
Средняя нагрузка генераторов - 0,9 РномДиапазон регулирования - (0,7 – 1,0) Рном
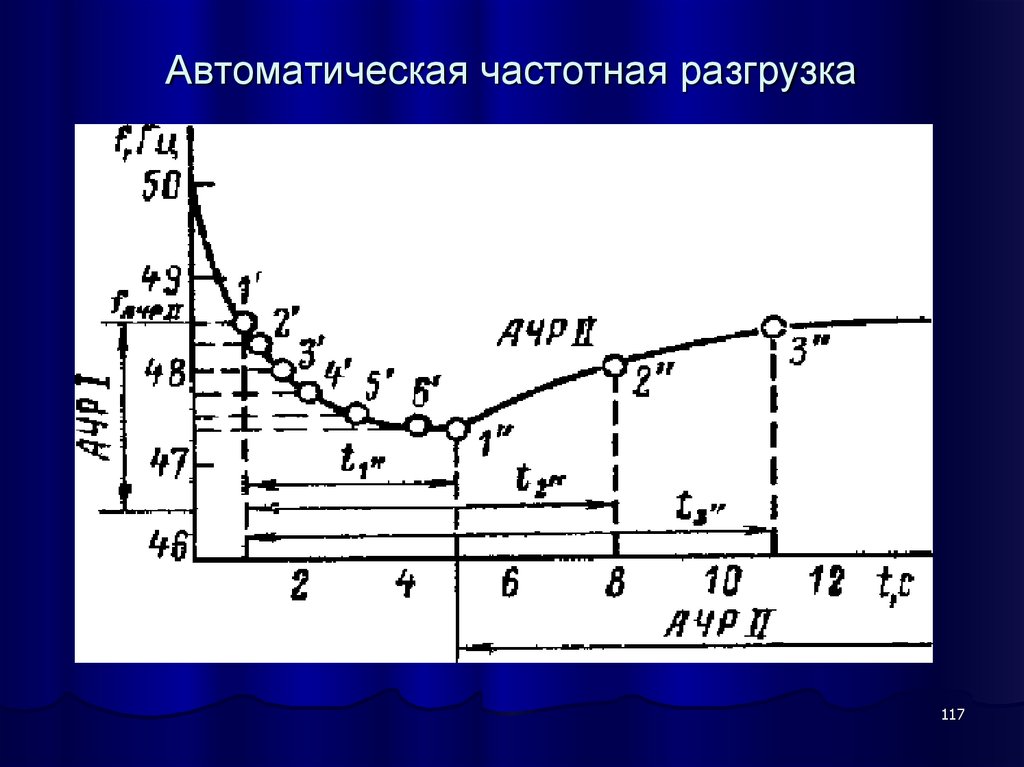
115. Автоматическая частотная разгрузка
Возникновение значительного дефицита активной мощности вотдельных ее частях (регионах) с глубоким (ниже 49,0 Гц)
снижением частоты создают угрозу повреждения оборудования
электростанций, безопасности работы АЭС, нарушения
нормальной работы потребителей вплоть до их полного
погашения. Для предотвращения этого в энергосистемах
применяется автоматическая частотная разгрузка (АЧР),
АЧР-I (быстродействующая АЧР
Задача АЧР-I : быстрое отключение части потребителей с целью
остановить лавинообразный процесс падения частоты в системе:
Диапазон уставок АЧР-I лежит от 48,8 Гц до 46,5 Гц с шагом в 0,1
Гц. Мощность отключаемых потребителей равномерно
распределяют по ступеням. Выдержка по времени у всех очередей
АЧР I одинаковая и лежит в пределах от 0,1 до 0,5 секунды.
115
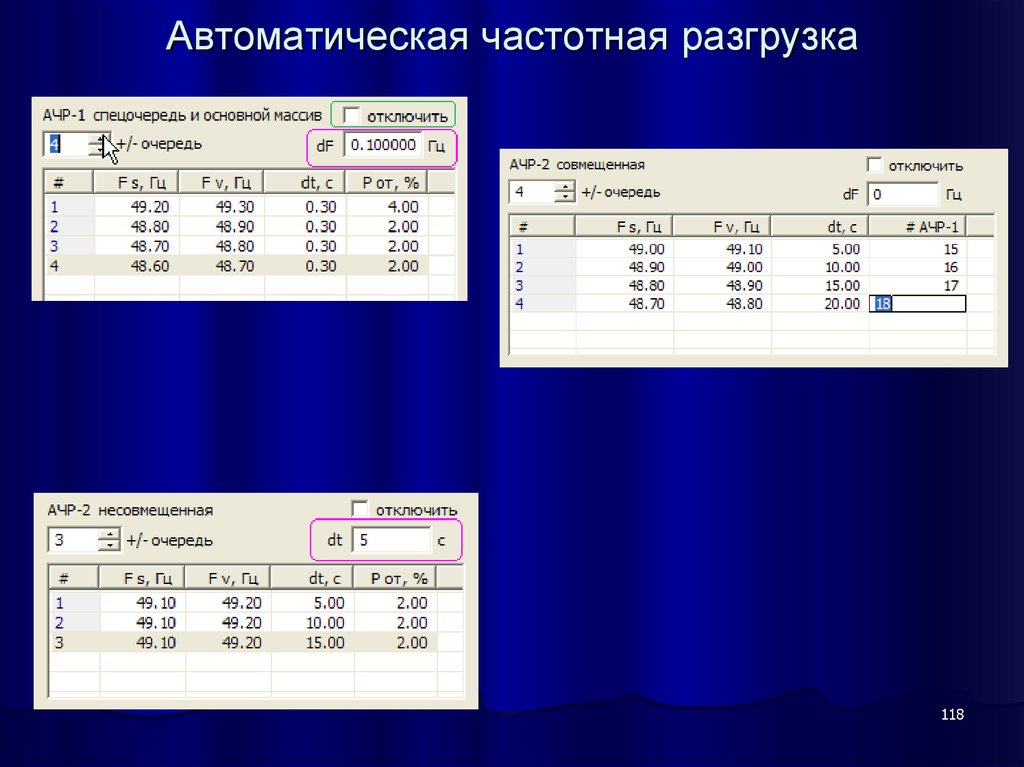
116. Автоматическая частотная разгрузка
АЧР-IIЗадача АЧР II: поднять частоту в системе после работы АЧР-I до
значений выше 49 Гц. Диапазон частот срабатывания АЧР-II – 48,6
– 48,8 Гц с шагом 0,1 Гц. Выдержка времени между ступенями
АЧР-II выбирается в диапазоне от 5 до 70 секунд ступенями по 3 5 секунд. Такая большая выдержка времени обусловлена тем, что
система может длительно работать при частоте выше 49,2 Гц,
поэтому быстро доводить значение частоты до номинального
путём отключения потребителей, которые могут получать
электроэнергию без особого вреда для системы, не имеет смысла.
Особые категории АЧР
спецочередь АЧР – для предотвращения автоматической или
оперативной разгрузки энергоблоков АЭС при снижении частоты
ниже 49,0 Гц;
дополнительная аварийная разгрузка – для ликвидации
значительных местных дефицитов мощности, действующая без
выдержки времени по скорости снижения частоты.
116
117. Автоматическая частотная разгрузка
117118. Автоматическая частотная разгрузка
118119. Структурная модель АРС гидроагрегата
119120. Модель гидравлической турбины
W ( p)M т ( p ) Tw p 1
Tw
( p )
p 1
2
1
dM т
d
2 M т
dt
T
dt
w
Me
Mт
K пр
Tw
-
Mт
время изменения скорости воды в водоводе
от нуля до номинальной, с
120
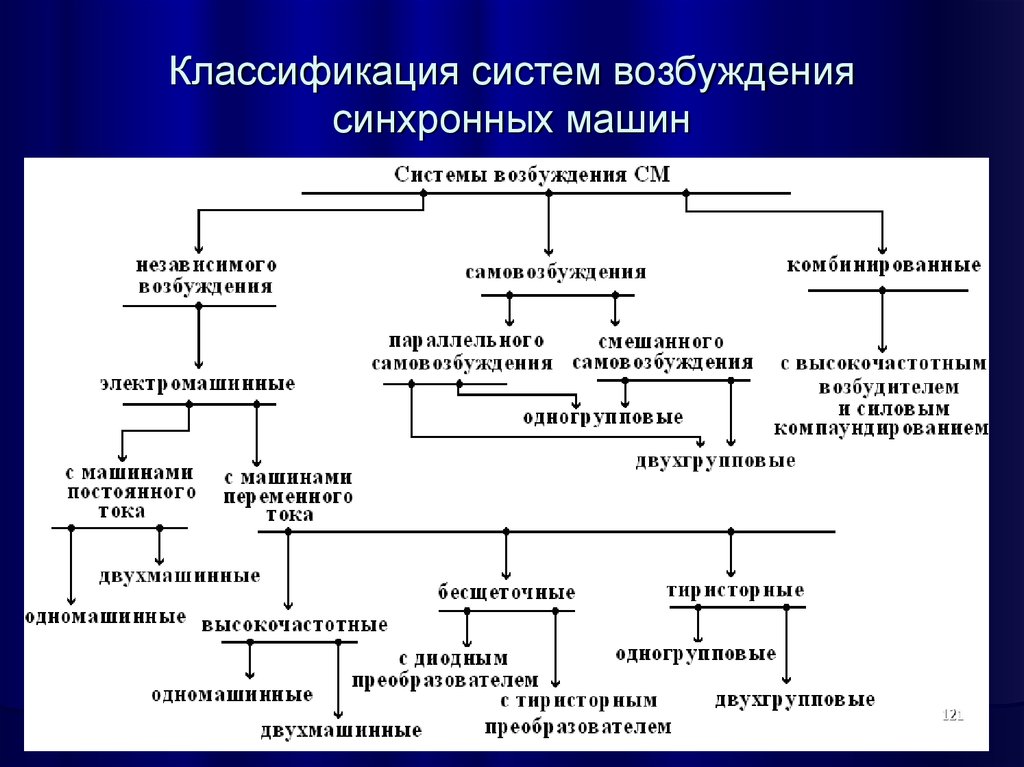
121. Классификация систем возбуждения синхронных машин
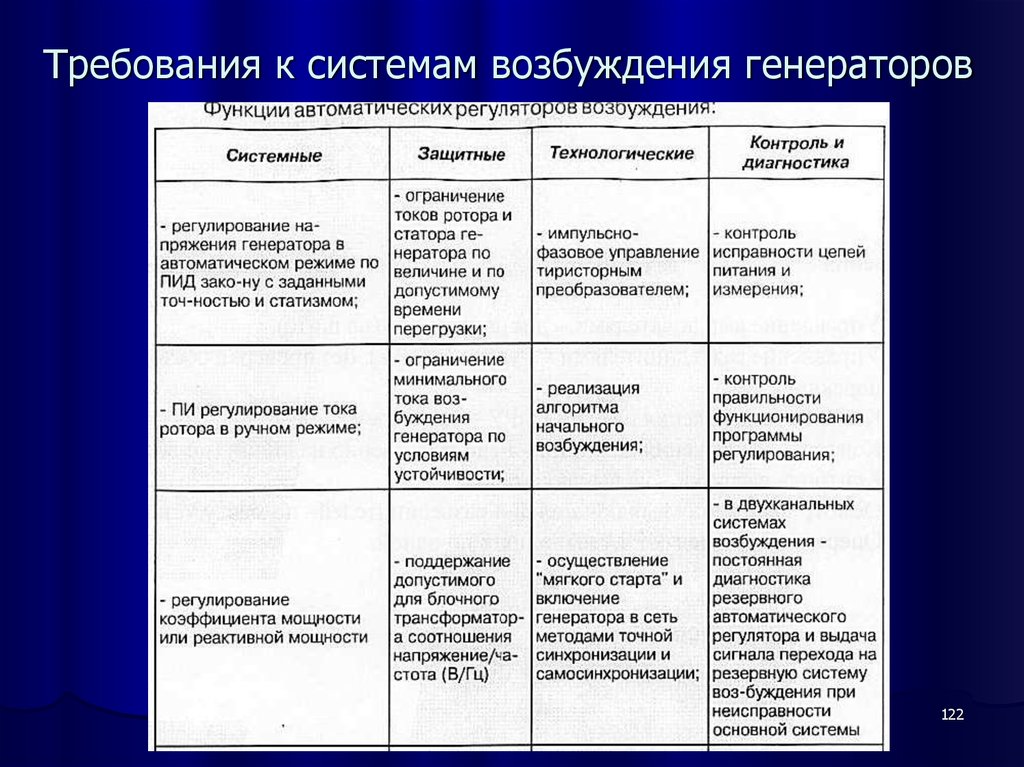
121122. Требования к системам возбуждения генераторов
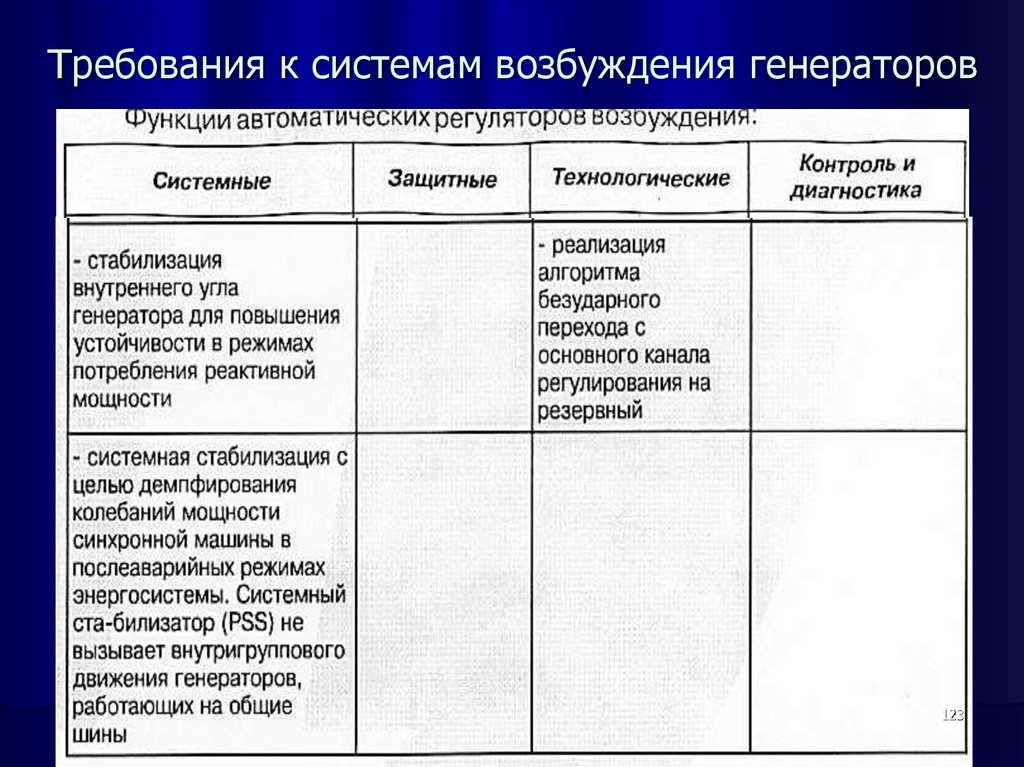
122123. Требования к системам возбуждения генераторов
123124. Требования к системам возбуждения генераторов
Имея необходимый набор моделей и компонентов систем124
125. Структурная модель электромашинной, высокочастотной (обычного исполнения) и тиристорной систем возбуждения
Независимоевозбуждение
Самовозбуждение без
последовательного
трансформатора
ВЧ-система с
диодным выпрямителем
125
126. Структурная модель бесщеточной и модернизированной высокочастотной (без компаундирования) систем возбуждения
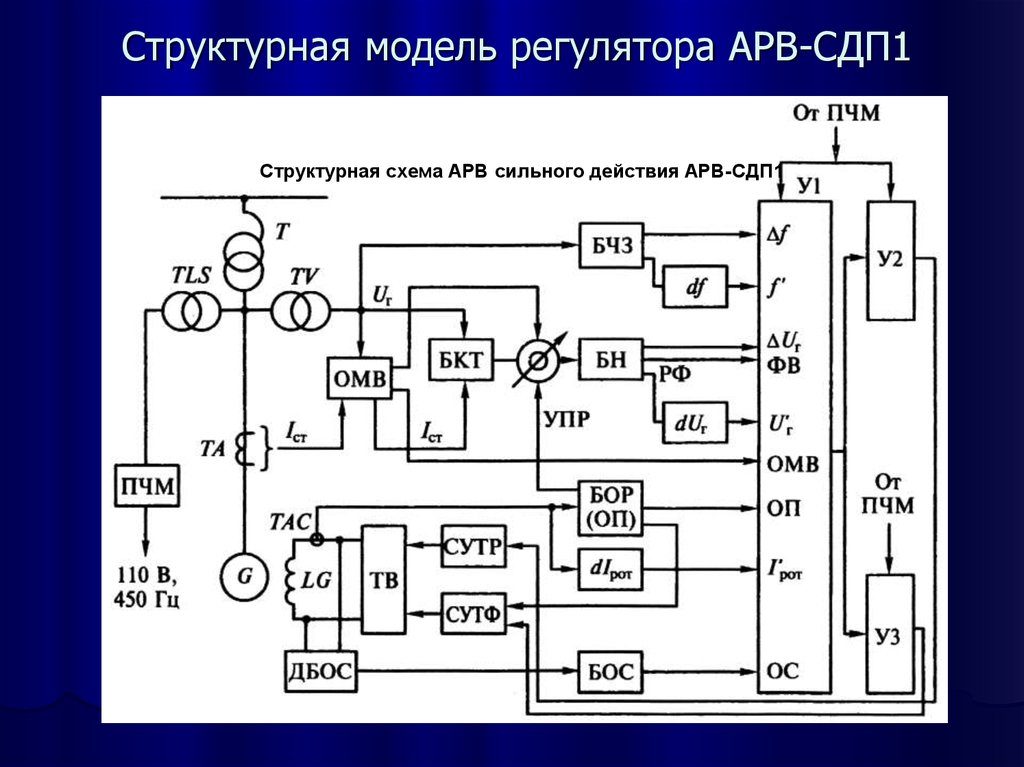
126127. Структурная модель регулятора АРВ-СДП1
Дополнив модель объекта звеньями, описывающими возбудитель и регуляторвозбуждения, можно получить полную структурную схему для исследования
внешнего движения. На первом этапе примем допущение о безынерционности АРВ
и возбудителя. Тогда их действие можно отразить, записав закон регулирования,
реализуемый собственно регулятором.
Регулятор АРВ СДП1, которым оснащаются все выпускаемые в странах СНГ
генераторы, является пропорционально-дифференциальным регулятором по
отклонению напряжения со стабилизацией режима по производной тока
возбуждения, отклонению и производной частоты напряжения. Модель
представляет собой совокупность функциональных узлов и блоков АРВ,
отражающих динамические свойства регулятора.
Физическими входами АРВ являются периодические сигналы измерительных
трансформаторов тока и напряжения, пропорциональные напряжению UГ и току IСТ
статора, току ротора IРОТ и суммарному току группы генераторов IΣ (последние на
схеме не показаны, служат для устойчивого распределения реактивной мощности
между параллельно работающими генераторами). Кроме того, в бесщеточных
системах возбуждения от блока обратной связи (БОС) на вход АРВ поступает сигнал
напряжения ротора UРОТ. Измерительные преобразователи формируют на основе
входной информации сигналы, которые для малых отклонений можно
интерпретировать как изменение напряжения ΔUГ, частоты напряжения Δf, тока
ΔIРОТ и напряжения ΔUРОТ ротора.
127










































































































 mathematics
mathematics








