Математическое моделирование. Понятие модели

1. ТЕМА: МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ ПОНЯТИЕ МОДЕЛИ

Модель – это материальный или мысленно
представляемый объект, который в процессе
изучения заменяет объект-оригинал, сохраняя
важные для данного исследования свойства.
Основное свойство модели: изучение модели
дает новые знания об объекте, позволяющие:
1. Выяснить структуру объекта, найти новые
свойства и закономерности.
2. Определить способы управления объектом.
3. Прогнозировать поведение объекта.

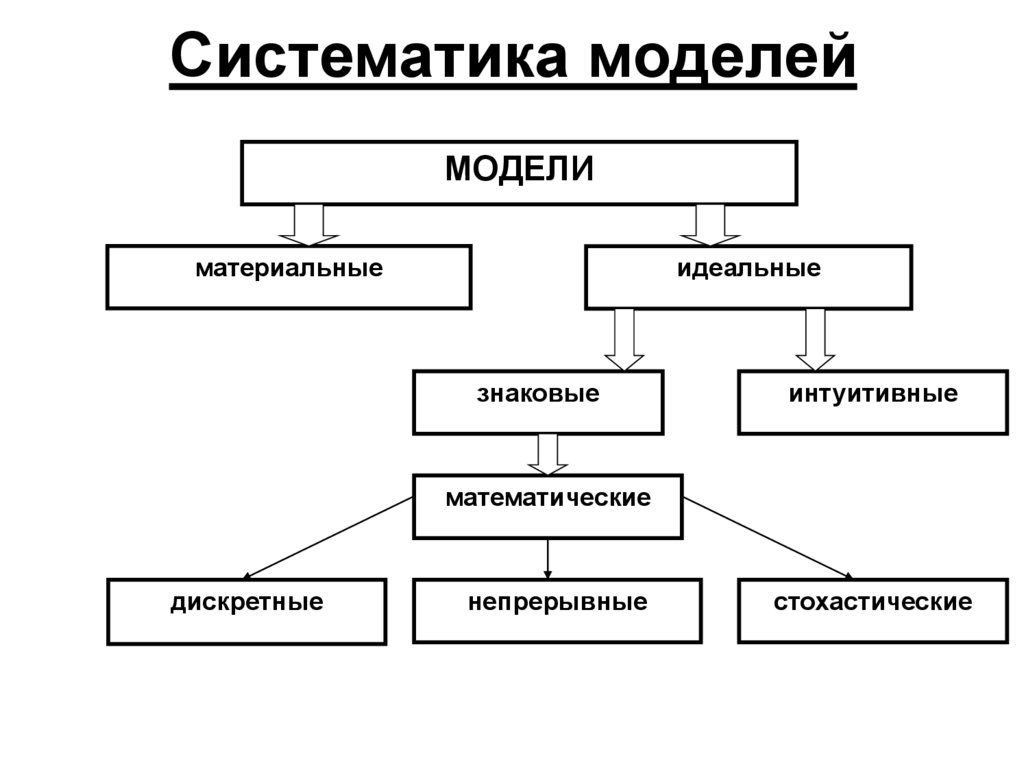
2. Систематика моделей

МОДЕЛИ
материальные
идеальные
знаковые
интуитивные
математические
дискретные
непрерывные
стохастические

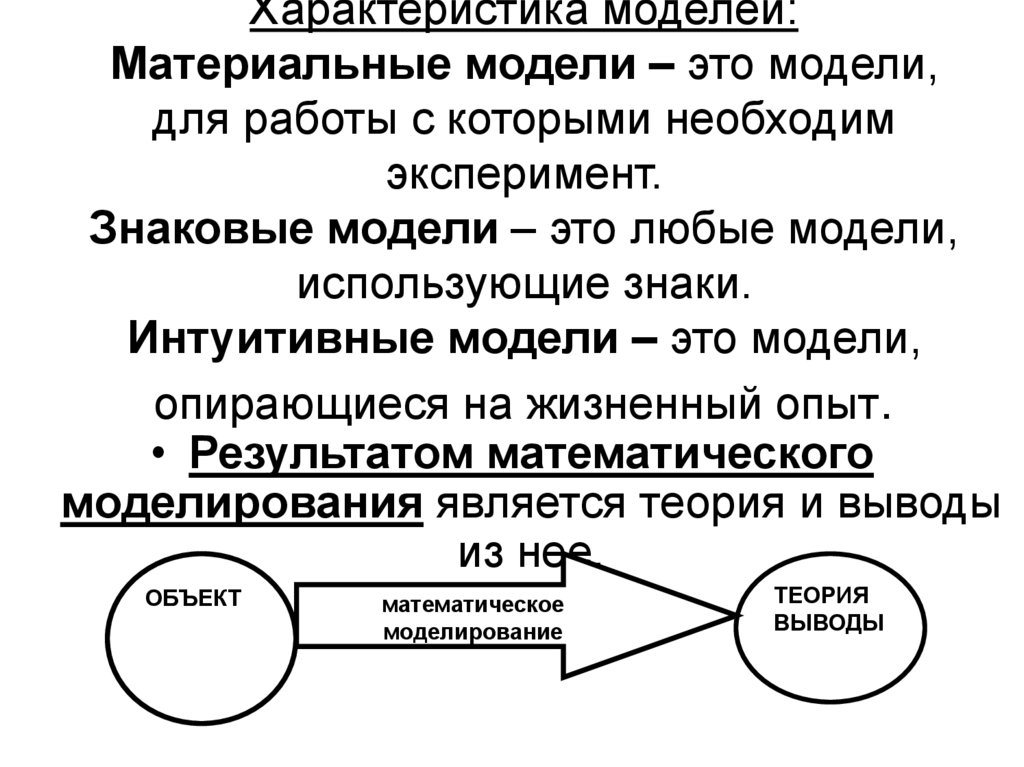
3. Характеристика моделей: Материальные модели – это модели, для работы с которыми необходим эксперимент. Знаковые модели – это

любые модели,
использующие знаки.
Интуитивные модели – это модели,
опирающиеся на жизненный опыт.
• Результатом математического
моделирования является теория и выводы
из нее.
ОБЪЕКТ
математическое
моделирование
ТЕОРИЯ
ВЫВОДЫ

4.

• Процесс моделирования:
• 1. Определение цели моделирования (что дано и что
требуется найти).
• 2. Определение факторов, которые нужно учесть.
• 3. Определение точности данных и требуемой
точности результата. Сопоставление их.
• 4. Построение нескольких моделей одного и того же
объекта (желательно).
• 5. Проверка адекватности модели.
• *Результат моделирования носит приближенный
или гипотетический характер!
• ** В каждой модели договариваются о
предположениях, выдвигают гипотезы.
Адекватность – это соответствие модели реальному объекту.
Адекватность проверяется здравым смыслом или сравнением
результатов моделирования с практическими результатами.

5. Задача баллистики.

ТЕМА: ПРИМЕРЫ МОДЕЛЕЙ, ПРИВОДЯЩИХ К
ДИФФЕРЕНЦИАЛЬНЫМ УРАВНЕНИЯМ
Задача баллистики.
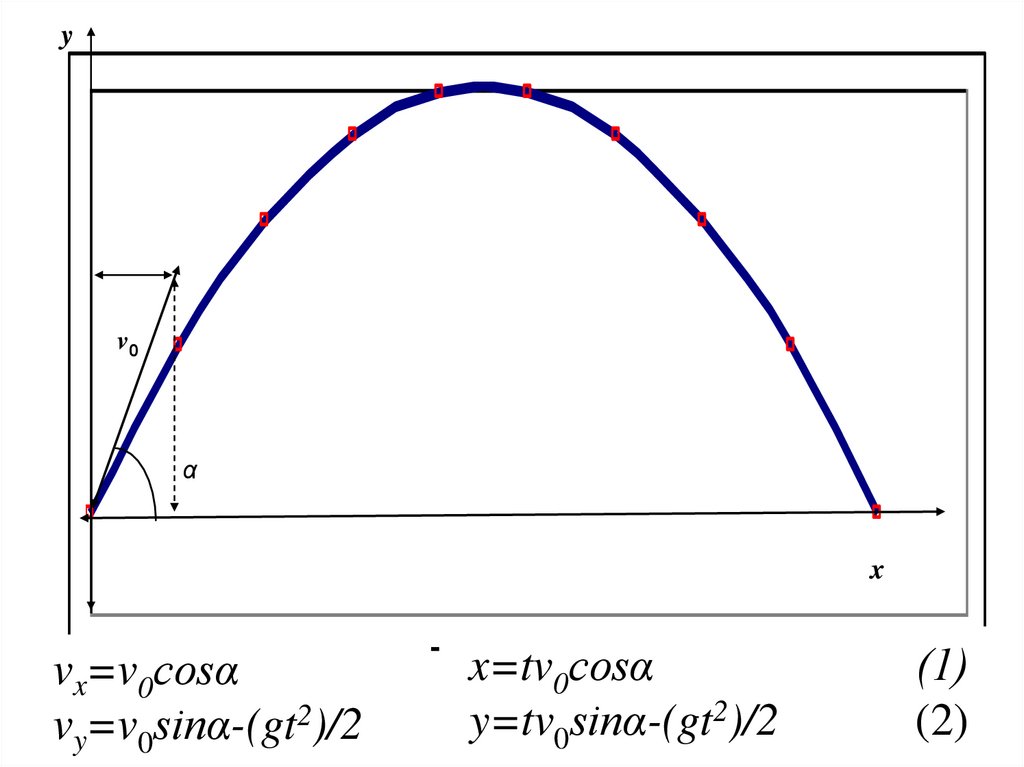
• Задача: из катапульты бросают камень с начальной
скоростью v0 под углом α к горизонту.
• Требуется определить траекторию полета камня и
дальность полета.
• Предположения модели:
• 1. Земля – инерциальная система отсчета.
• 2. Ускорение свободного падения g постоянно.
• 3. Кривизной Земли можно пренебречь.
• 4. Сопротивлением воздуха можно пренебречь.

6. x=tv0cosα (1) y=tv0sinα-(gt2)/2 (2)

y
v0
α
x
vx=v0cosα
vy=v0sinα-(gt2)/2
x=tv0cosα
y=tv0sinα-(gt2)/2
(1)
(2)

7. Выражаем t из (1) и подставляем в (2). Получаем уравнение траектории:

x
gx 2
x2 g
y ( x)
v0 sin 2
xtg 2
2
v0 cos
2v0 cos
2v0 cos 2
Чтобы определить дальность полета, нужно решить
уравнение:
x2 g
xtg 2
0
2
2v0 cos
х1=0;
tg 2v02 cos 2 2v02 cos 2 sin v02 sin 2
x2
g
g cos
g
формула для определения дальности полета.
v02 sin 2
x2
g

8.

Задача баллистики с учетом силы
сопротивления воздуха.
• Из предположений модели исключаем
предположение №4.
Предположения модели:
• 1. Земля – это инерциальная система отсчета.
• 2. Ускорение свободного падения g постоянно.
• 3. Кривизной Земли можно пренебречь.
• 4. Сопротивлением воздуха можно пренебречь.

9.

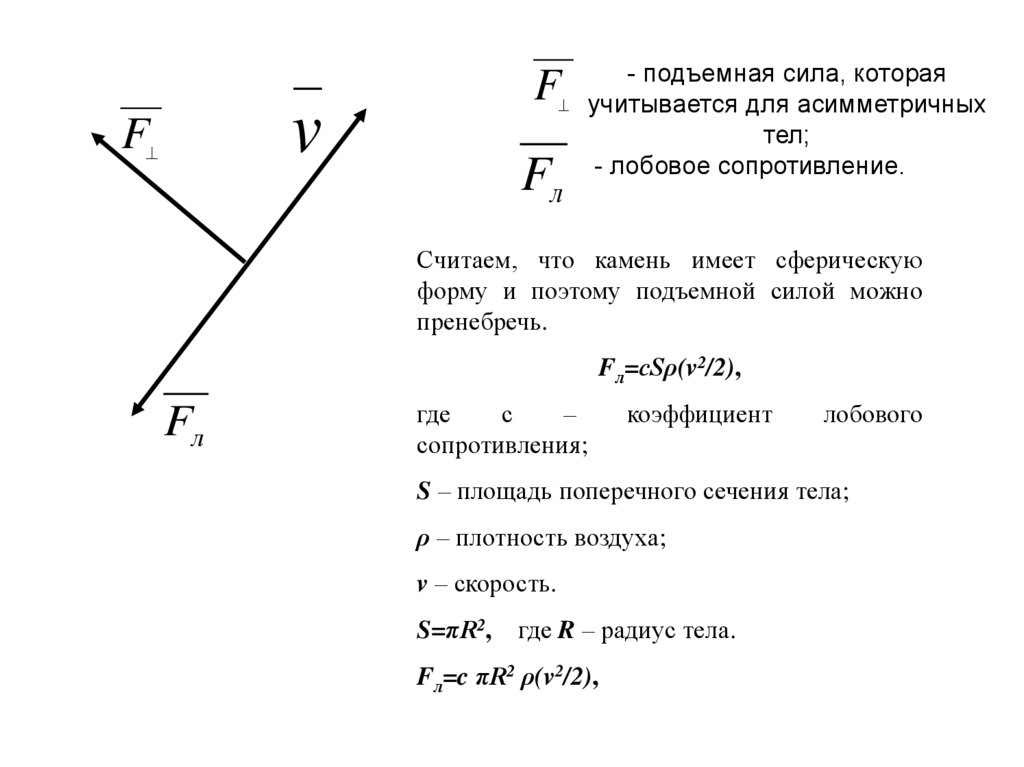
- подъемная сила, которая
F учитывается
для асимметричных
v
F
Fл
тел;
- лобовое сопротивление.
Считаем, что камень имеет сферическую
форму и поэтому подъемной силой можно
пренебречь.
Fл=cSρ(v2/2),
Fл
где
с
–
сопротивления;
коэффициент
лобового
S – площадь поперечного сечения тела;
ρ – плотность воздуха;
v – скорость.
S=πR2,
где R – радиус тела.
Fл=c πR2 ρ(v2/2),

10.

ma P Fл
Р – сила тяжести.
P mg j Fл Fлx i Fлx j
л
y
лх
vy
v
х
Fv
F
v
л
лх
Fлx j
i
Fлx
Fл
Fл
v
Fлy v y
F
v
F
v
vx
x
x
Fv
F
v
Fл v y
vx
Fл Fл i
j
v
v
Знак «минус» показывает
противоположное направление
скорости.
л
лy
y

11.

Подставляем Fл в уравнение (*):
Fv
v
ma F i (m g
)j
v
v
л
x
y
л
Разделим обе части уравнения на
m:
Fv
Fv
a
i (g
)j
mv
mv
л
л
x
y
Перейдем от этого уравнения к
скалярным уравнениям:
c R 2v vx
ax
;
2m
Fл vx
ax
;
mv
Fv
a g
;
mv
л
y
y
v v v
2
x
c R v v
a g
2m
2
y
y
2
y

12.

x(t)≡x
y(t)≡y
vx=x’
c R
x
'
'
(
x
'
)
(
y
'
)
x
'
2m
c
R
y' ' g
(
x
'
)
(
y
'
)
y
'
2m
2
2
2
2
vy=y’
ax=x’’
2
ay=y’’
Чтобы решить эту систему, нужно знать начальные условия.
Начальные условия:
x(0)=0;
x’(0)=v0cosα;
y(0)=0; y’(0)=vosinα;
Сменим обозначения:
x→U1;
x’→U2;
y→U3;
y’→U4.
2

13.

dU
dt
dU
dt
dU
dt
dU
dt
1
U ;
2
2
3
c R
2m
2
U U U ;
2
2
2
4
2
U ;
4
4
c R
g
2m
Начальные условия:
U1(0)=0;
U2(0)=v0cosα;
U3(0)=0;
U4(0)=v0sinα.
2
U U U .
2
2
2
4
4
Решением этой системы будут функции при
заданных начальных условиях.

14.

15.

ТЕМА: КРАЕВАЯ ЗАДАЧА
Постановка задачи. Снаряд летит с постоянной скоростью под углом α к горизонту.
Цель находится на расстоянии l.
Угол α мы можем менять.
Вопрос: как стрелять?
v0
α
l

16.

Система дифференциальных уравнений:
dU
dt U ;
dU c R U U U ;
dt
2 m
dU U ;
dt
dU
c R
g
U U U .
dt
2m
1
2
2
2
2
2
2
4
2
3
4
2
4
2
2
2
4
4
Граничные условия (начальные условия, которые задаются на концах отрезка):
U ( 0) 0;
U (0) 0;
t конечное
U (t конечное ) l ;
U (t конечное ) 0.
1
3
1
3

17.

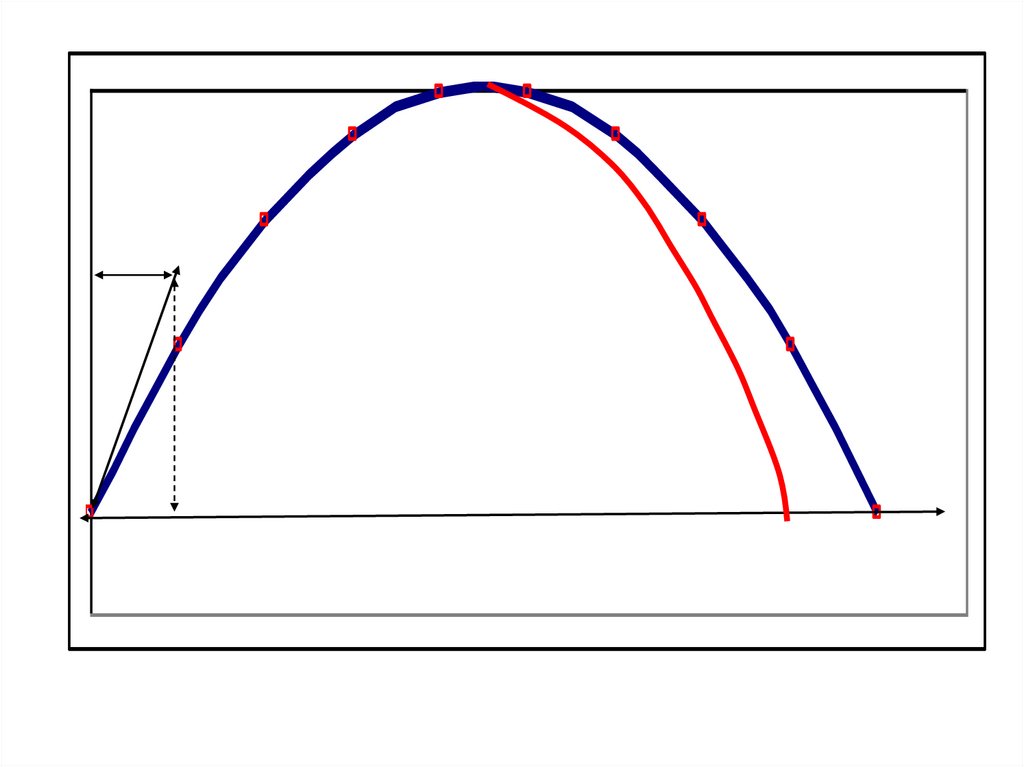
Дальность полета максимальна при α=45º.
Мы можем решить задачу Коши
при α =45º. Получим некоторую траекторию, которая будет больше, чем нужно.
Уменьшим угол α. Возьмем α1<45º и снова решим задачу Коши.
Получим новую траекторию. Здесь 2 варианта – перелет или недолет.
Маловероятно, что мы попадаем в цель. После этого снова меняем угол α:
x(tk)=l;
|x(tk)-l|≤ε.
При достижении заданной точности ε мы можем прекратить решение задачи
и считать полученное решение окончательным решением краевой задачи.

18.

Задача Коши в векторной
форме:
Y F ( x, Y )
y1 ( x)
где:
y2 ( x)
Y ( x)
...
yn ( x)
y ( x)
1
Y y2 ( x)
yn ( x)
где
Y
— вектор, содержащий решение,
f1 ( x, y1 ,..., yn )
f 2 ( x, y1 ,..., yn )
F ( x, Y )
...
f ( x, y ,..., y )
n 1 n
Y0
Y ( x 0 ) Y0
y0
y01
Y0
...
y
0 ,n 1
— вектор начальных условий, а
F ( x, Y )
— вектор правых частей.

19.

Задача Коши для системы
нормальных
дифференциальных
уравнений
?
Функция rkfixed
РЕШЕНИЕ ЗАДАЧИ
КАК ЭТО СДЕЛАТЬ В MATHCAD?

20.

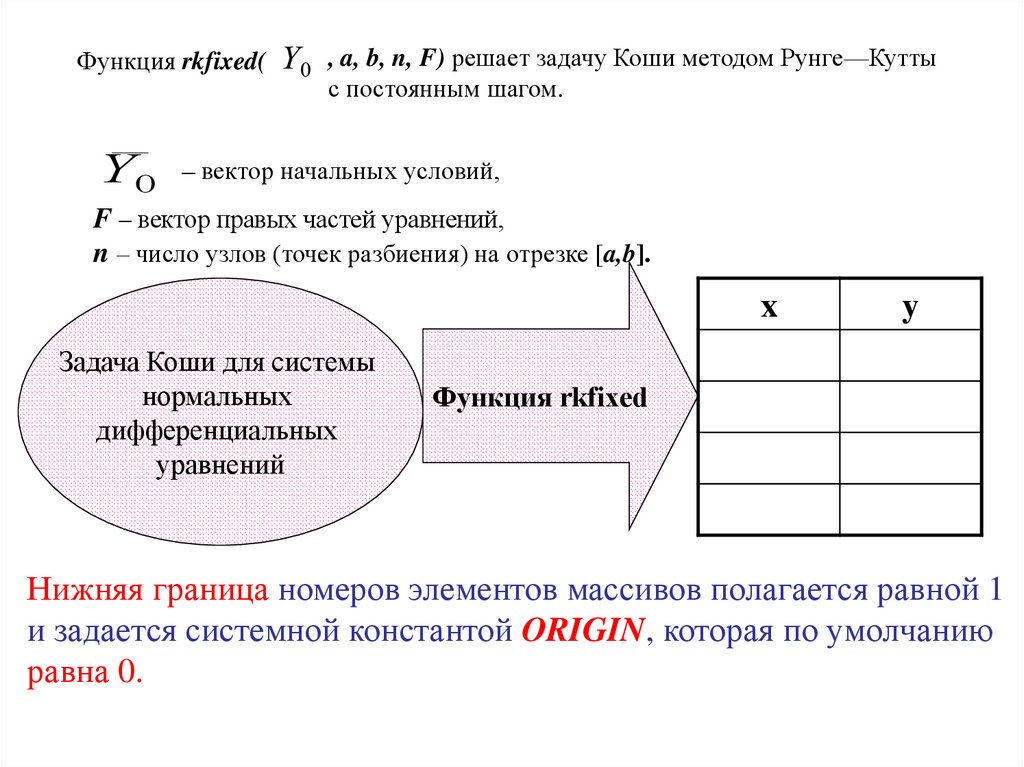
Функция rkfixed( Y0 , a, b, n, F) решает задачу Коши методом Рунге—Кутты
с постоянным шагом.
Y0 – вектор начальных условий,
F – вектор правых частей уравнений,
n – число узлов (точек разбиения) на отрезке [a,b].
x
Задача Коши для системы
нормальных
дифференциальных
уравнений
y
Функция rkfixed
Нижняя граница номеров элементов массивов полагается равной 1
и задается системной константой ORIGIN, которая по умолчанию
равна 0.

21.

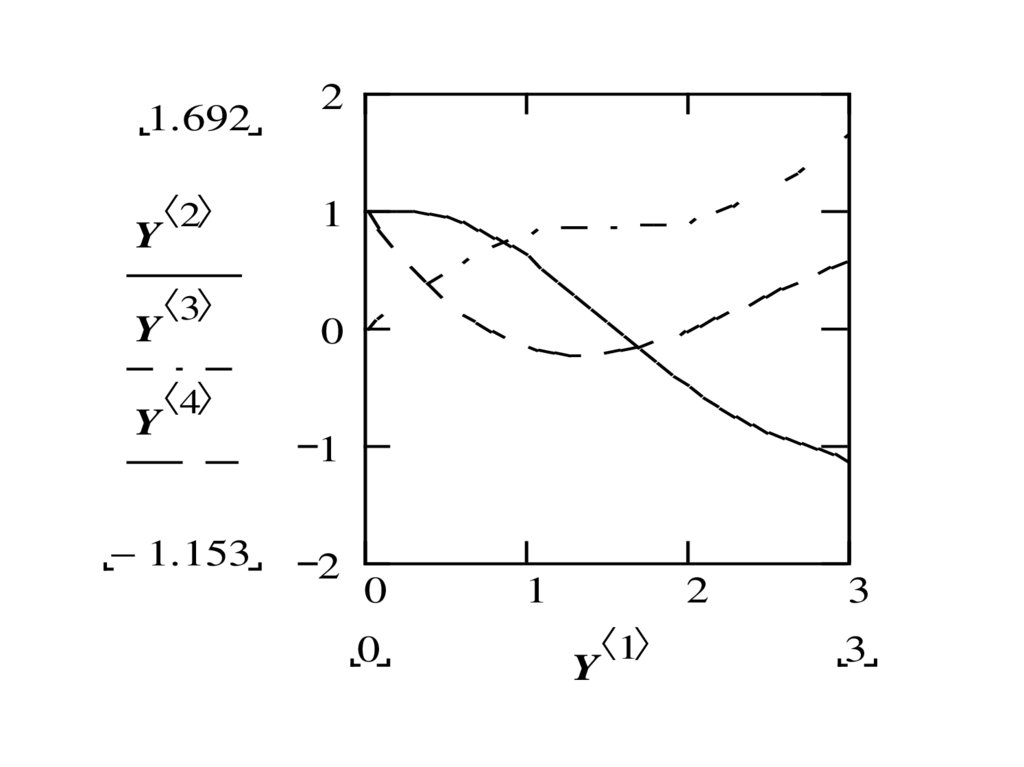
Пример. Решить систему дифференциальных уравнений на отрезке [0,3] с
шагом 0.1, построить графики найденных функций.
y y sin xy
2
3
1
2
y
y
2
1
y 3 y 3 y1
y1 ( 0 ) 1
y 2 ( 0) 0
y ( 0) 1
3
Решение в Mathcad
ORIGIN 1
y sin x y
3
2
2
F ( x y)
y
1
y y
3
1
1
y0 0
1
Y rkfixed y0 0 3 30 F

22.

1.692
Y
Y
Y
2
3
2
1
0
4
1.153
1
2
0
0
1
2
Y
1
3
3

23.

Модель развития науки.
В этой модели учитывается
один показатель: количество
публикаций в данный момент.
х(t)≡х;
ПРЕДПОЛОЖЕНИЕ: скорость
роста количества публикаций
пропорциональна их
количеству в данный момент
времени.

24.

Запишем дифференциальное уравнение:
dx
kx
dt
Решением уравнения такого вида является функция
вида еt; et→∞; t→∞.
Пусть b – уровень насыщения. Тогда дифференциальное уравнение
можно записать следующим образом:
dx
k (b x)
dt
х→b
или
dx
0;
dt

25.

Модель численности популяций.
N(t) – численность популяции в момент времени t.
Скорость v роста популяции прямо пропорциональна ее численности
в данный момент времени.
dN
N
dt
где μ – разность между коэффициентом смертности и коэффициентом
рождаемости.
Если μ>0, то численность популяции неограниченно растет, т.е. N→∞.
Пусть b – емкость среды. Тогда дифференциальное уравнение
запишется следующим образом:
dN
(b N )
dt
dN
Если N→b, то
0.
dt

26.

Пример 3. Модель гонки вооружений Ричардсона.
x(t)≡x – расходы на вооружение «зеленых»;
y(t)≡y – расходы на вооружение «желтых».
ПРЕДПОЛОЖЕНИЕ 1: Затраты «зеленых» зависят от уровня затрат
«желтых», и наоборот.
dx
ay;
dt
dy
bx.
dt
Начальные условия:
x(t ) x ;
0
0
x(t ) 0;
y(t ) 0; y(t ) y ; a, b 0.
0
0
ПРЕДПОЛОЖЕНИЕ 2: скорость роста затрат на
вооружение уменьшается с ростом самих затрат.
Чем больше х, тем меньше dx/dt.

27.

dx
ay mx;
dt
dy bx ny;
dt
m 0;
n 0.
ПРЕДПОЛОЖЕНИЕ 3: Предположим, что у каждого государства могут быть какието претензии.
Введем коэффициенты претензий r и s.
r,s≥0 – коэффициенты претензий;
r,s<0 – коэффициент доброй воли.
Система уравнений запишется так:
dx
ay mx r ;
dt
dy bx ny s.
dt
Начальные условия:
x(t ) x ;
0
0
x(t ) 0;
y(t ) 0; y(t ) y ;
0
0
a, b, n, m 0.

28.

КОГДА ДОСТИГАЕТСЯ РАВНОВЕСИЕ?
Точка равновесия достигается при следующем условии:
dx
dy
0.
dt
dt
ay mx r 0;
bx ny s 0.
x=(a/m)y+(r/m);
x=(n/b)y-s/b;
(a/m)y+r/m= (n/b)y-s/b;
y(a/m-n/b)=-s/b-r/m.

29.

Точка, в которой достигается равновесие, имеет следующие координаты:
s / b r / m sm rb
y
n / b a / m nm ab
sm rb
x a / m
r/m
nm ab
Каждая точка этой координатной плоскости
характеризуется:
1. Координатами х и у.
2. Моментом времени t.
3. Скоростью изменения координат dx/dt и
dy/dt.

30.

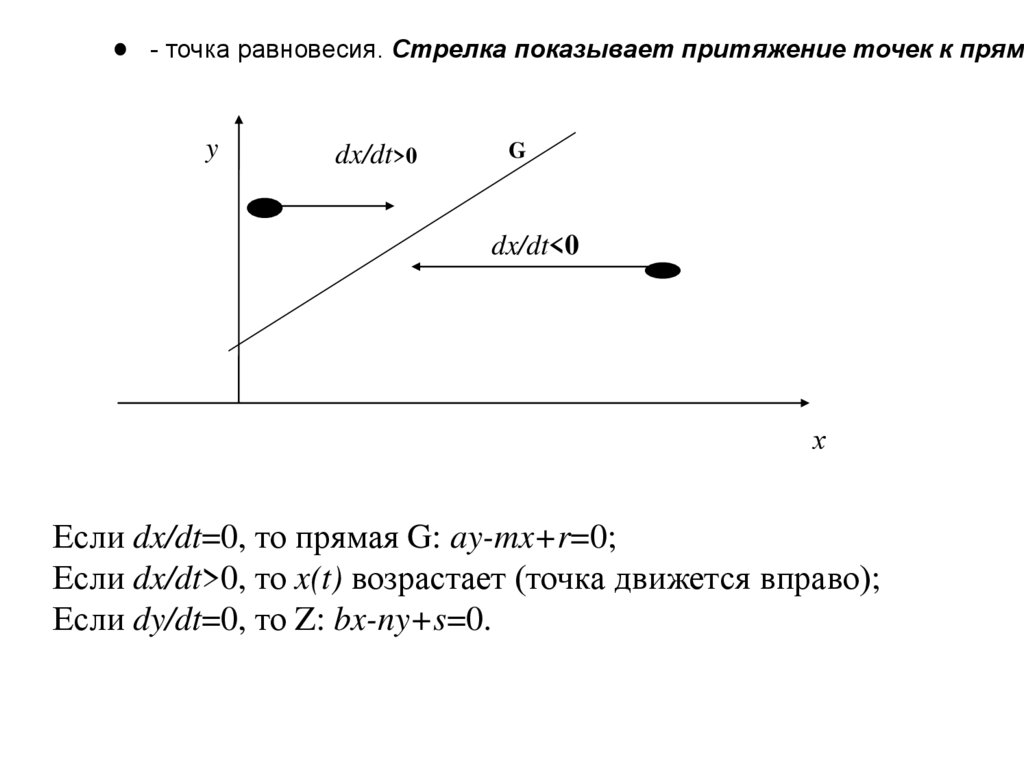
- точка равновесия. Стрелка показывает притяжение точек к прямо
y
dx/dt>0
G
dx/dt<0
х
Если dx/dt=0, то прямая G: ay-mx+r=0;
Если dx/dt>0, то x(t) возрастает (точка движется вправо);
Если dy/dt=0, то Z: bx-ny+s=0.

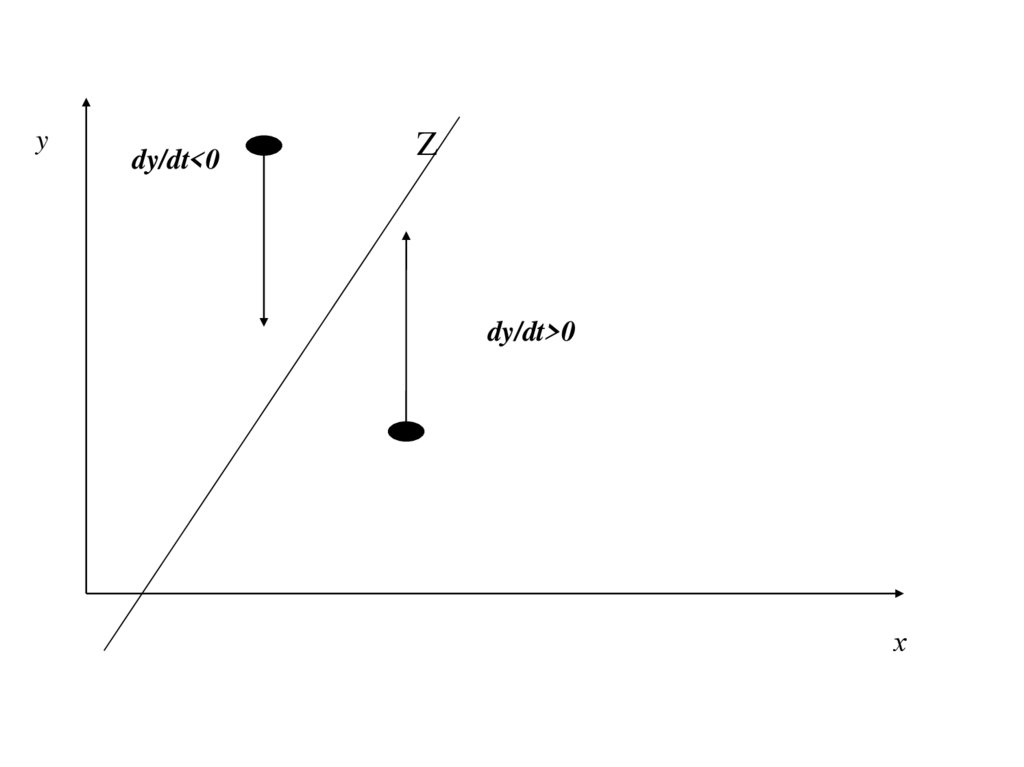
31.

y
dy/dt<0
Z
dy/dt>0
х

32.

Исследуем поведение системы в зависимости от начальных условий.
В зависимости от коэффициентов m, n, r, s
положение точки равновесия может быть различным.
Рассмотрим следующие варианты:
Вариант 1. mn-ab>0;
r,s>0.
! При любых начальных условиях есть стремление к точке равновесия!
G:
y=(m/a)x-r/a
Z:
y=(b/n)x+s/n.
m/a-b/n=(mn-ab)/an>0,
т.е. коэффициент m/a прямой G больше коэффициента прямой Z,
следовательно, угол наклона прямой G больше.
G
z

33.

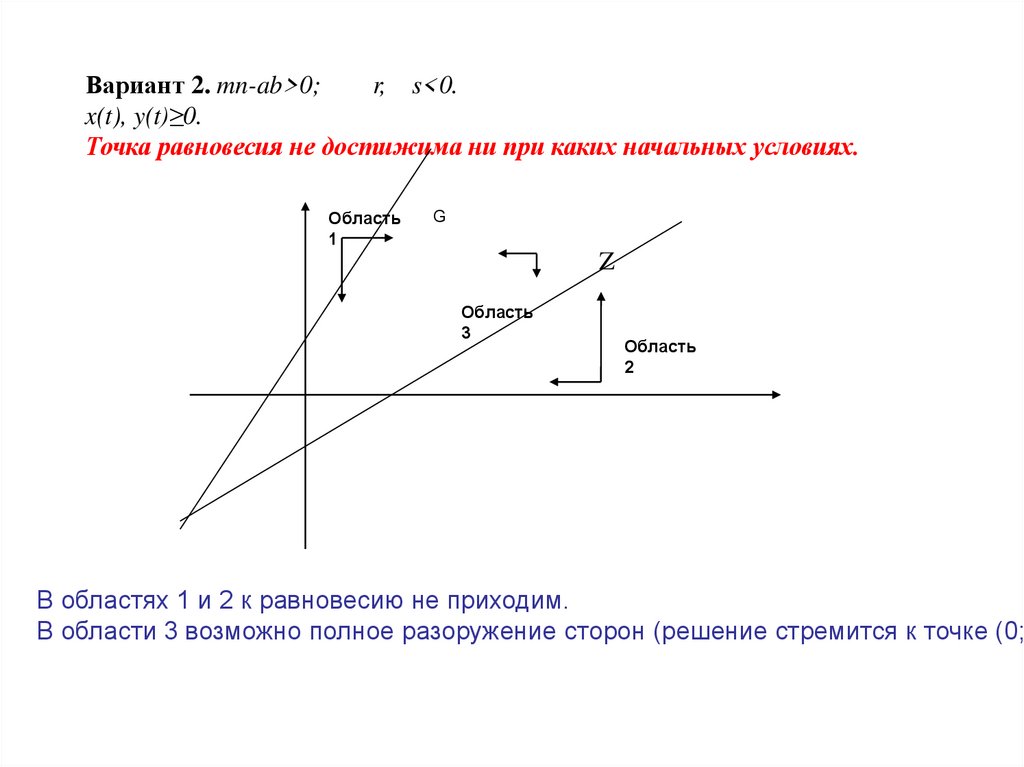
Вариант 2. mn-ab>0;
r, s<0.
x(t), y(t)≥0.
Точка равновесия не достижима ни при каких начальных условиях.
Область
1
G
Z
Область
3
Область
2
В областях 1 и 2 к равновесию не приходим.
В области 3 возможно полное разоружение сторон (решение стремится к точке (0;0

34.

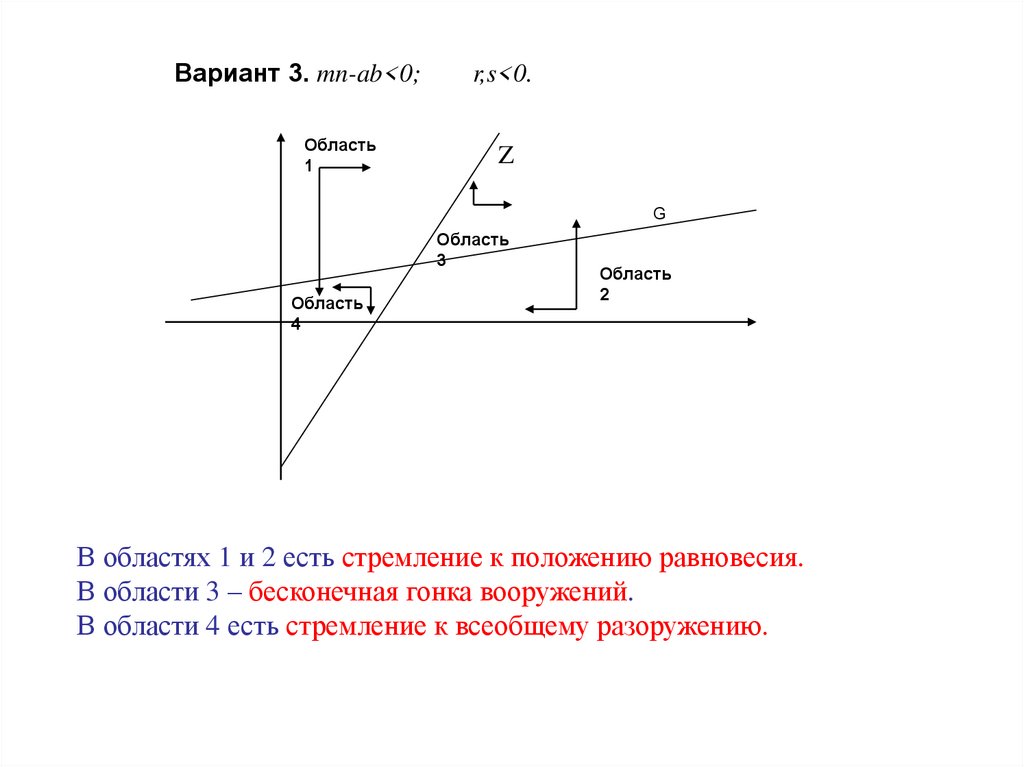
Вариант 3. mn-ab<0;
Область
1
r,s<0.
Z
G
Область
3
Область
4
Область
2
В областях 1 и 2 есть стремление к положению равновесия.
В области 3 – бесконечная гонка вооружений.
В области 4 есть стремление к всеобщему разоружению.

35.

ПРОВЕРКА АДЕКВАТНОСТИ МОДЕЛИ делалась на реальных данных.
Рассматривались 2 блока:
х – Россия и Франция;
у – Германия и Австро-Венгрия.
dx
ay mx r ;
dt
dy bx ny s.
dt
ПРЕДПОЛОЖЕНИЕ: а=b; m=n.
При таком предположении система
перепишется следующим образом:
Складываем два уравнения:
d(x+y)/dt=(a-m)y+(a-m)x+r+s.
dx
ay mx r ;
Пусть a-m=k, а r+s=f.
dt
z=x+y. - суммарные затраты на вооружение 2-х блоков
dy ax my s.
dt
dz/dt=kz+f – это уравнение можно использовать
для анализа.

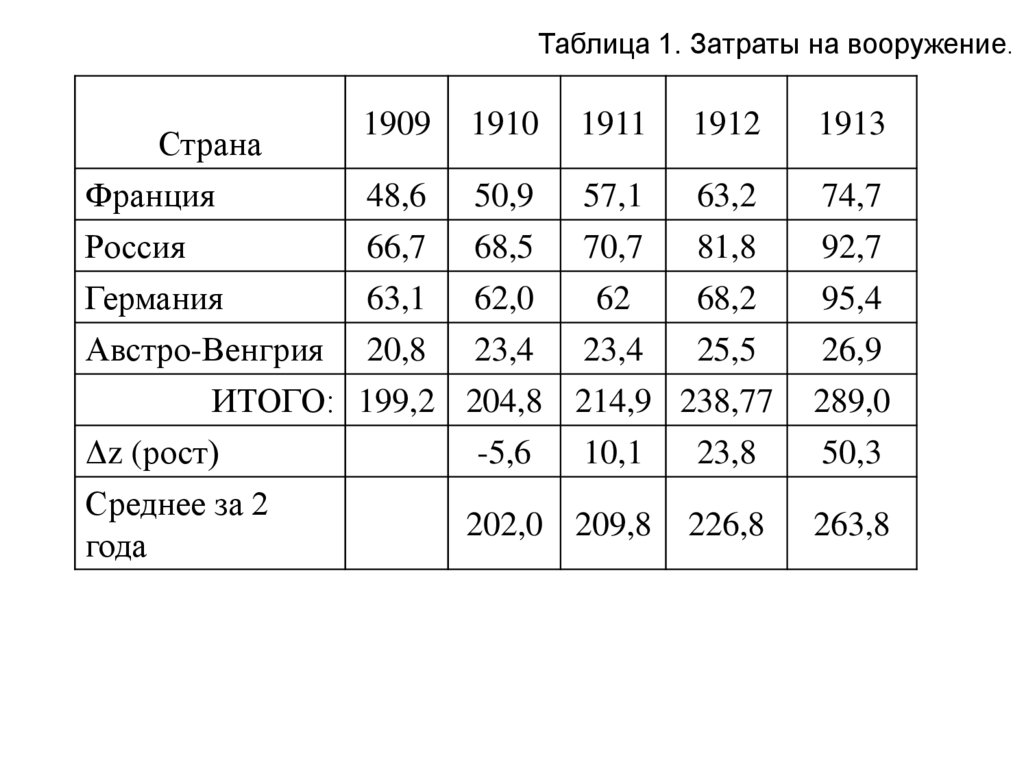
36.

Таблица 1. Затраты на вооружение.
Страна
Франция
1909
1910
1911
1912
1913
48,6
50,9
57,1
63,2
74,7
Россия
Германия
Австро-Венгрия
66,7
63,1
20,8
68,5
62,0
23,4
70,7
62
23,4
81,8
68,2
25,5
92,7
95,4
26,9
ИТОГО: 199,2 204,8 214,9 238,77
Δz (рост)
-5,6
10,1
23,8
Среднее за 2
202,0 209,8 226,8
года
289,0
50,3
263,8

37.

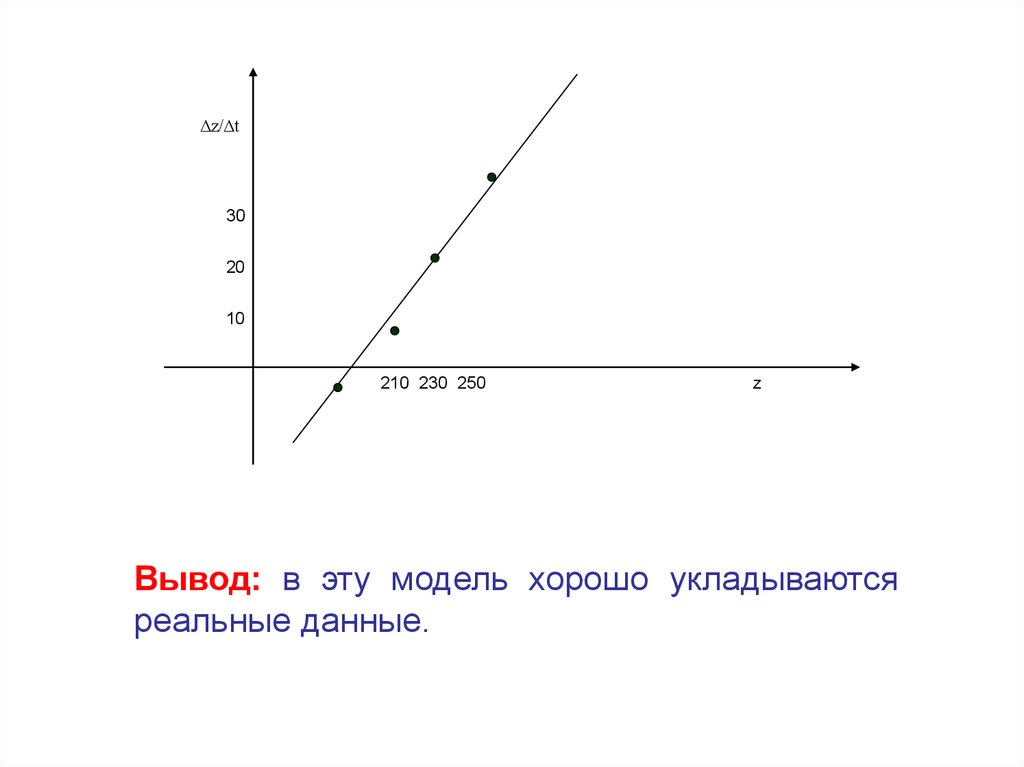
Δz/Δt
30
20
10
210 230 250
z
Вывод: в эту модель хорошо укладываются
реальные данные.

38.

Моделирование прогиба балки

39. Моделирование прогиба балки

Q
0
P
φ(S)
S
y
x
Q
P
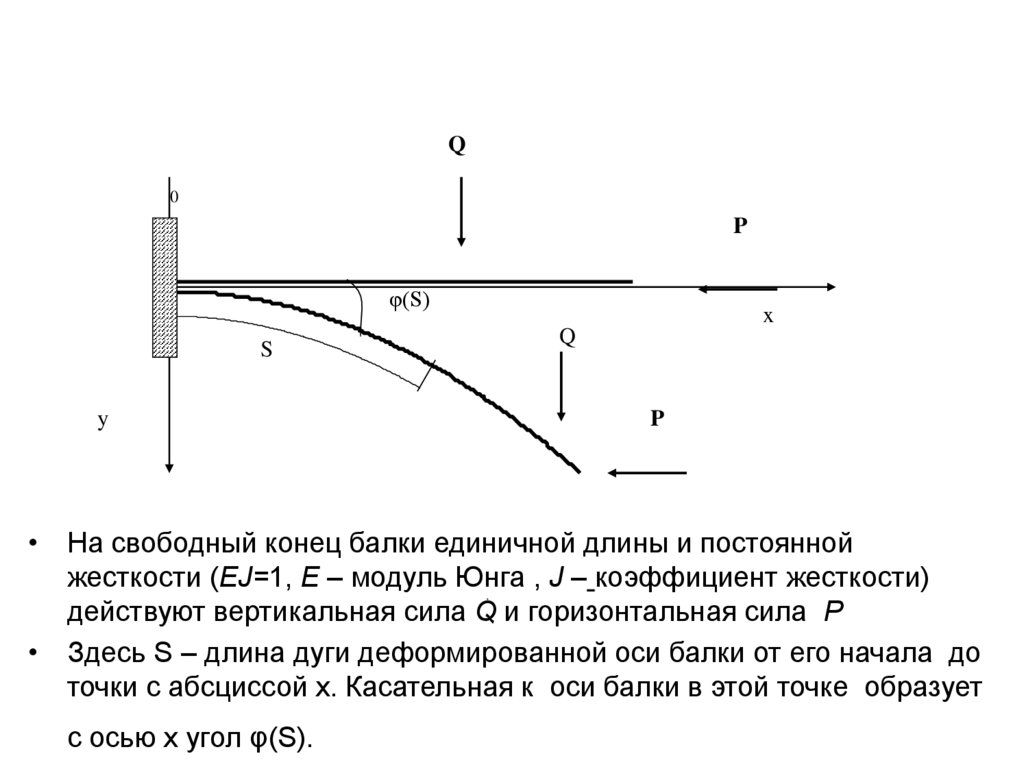
• На свободный конец балки единичной длины и постоянной
жесткости (ЕJ=1, Е – модуль Юнга
, J – коэффициент жесткости)
.
действуют вертикальная сила Q и горизонтальная сила P
• Здесь S – длина дуги деформированной оси балки от его начала до
точки с абсциссой х. Касательная к оси балки в этой точке образует
с осью х угол φ(S).

40.

• Прогиб балки описывается нелинейным
дифференциальным уравнением :
• с граничными условиями:
• . d 2
dS
2
Q cos P sin 0,
с граничными условиями:
(0) 0, (1) 0
S [0,1]
.

41.

Если известно φ(S), то декартовы координаты точек
изогнутой оси балки можно определить из следующих
соображений:
малому изменению декартовых координат Δх и Δу
соответствует малое изменение длины дуги стержня ΔS.
Малый отрезок дуги можно заменить отрезком прямой, и
тогда Δх= ΔS cosφ, Δу= ΔS sinφ. Отсюда
~
S
~
S
~
~
x(S ) cos ds, y( S ) sin ds
0
0
Задавая различные значения Р и Q, можно построить
кривые у(х) при заданных нагрузках.

42.

Решение задачи КОШИ
для обыкновенного дифференциального уравнения
odesolve(x,b,step),
• Обращение к функции имеет вид y:=odesolve(x,b) или
y:=odesolve(x,b,step),
• где y – имя функции, содержащей значения найденного
решения,
• x — независимая переменная,
• b — конец промежутка интегрирования,
• step – шаг (можно не указывать).
• Перед обращением к функции odesolve надо записать
ключевое слово given, затем ввести уравнение и начальные
условия. При вводе уравнения и начальных условий
используется знак символьного равенства. При записи
неизвестной функции в уравнении обязательно требуется
указать в скобках аргумент – независимую переменную.
Производную можно записывать как , так и (знак производной
ставится сочетанием клавиш Ctrl и F7). Аналогично
записываются и производные высших порядков.

43. Решение задачи КОШИ для обыкновенного дифференциального уравнения odesolve(x,b,step),

Решение в Mathcad
given
''( s) Q cos ( s) P sin ( s)
( 0)
0
'( 1)
0
0
odesolve( s 1)
s
x ( s) cos ( s) d s
0
s
y( s) sin ( s) d s
0

44.

Применение метода конечных разностей
• дифференциальная задача сводится к решению
системы алгебраических уравнений.
Длина балки разбивается на n равных интервалов длиной h.
В каждой точке разбиения записывается исходное дифференциальное
уравнение, при этом во всех узлах сетки, кроме нулевого, вторая производная
заменяется ее конечно-разностной аппроксимацией:
d i 1 2 i i 1
, i 1,..., n.
2
2
dS
h
2
При i = 0 учет первого краевого условия дает .
0 0

45. Применение метода конечных разностей

При для аппроксимации производной требуется значение угла
φn+1 в несуществующем узле с номером n+1. Оно определяется из
второго краевого условия:
d n 1 n 1
0
ds
2h
Отсюда
n 1 n 1
В итоге имеем систему нелинейных уравнений, решением
i
которой являются значения угла
в точках разбиения:
2 1 2 (Q cos 1 P sin 1 )h 2 0,
i 1
2
2
(
Q
cos
P
sin
)
h
0, i 2,..., n 1
i 1
i
i 1
i
i
2
2 n 1 2 n (Q cos n P sin n )h 0, i n

46.

• При малых прогибах балки можно считать
cos( i ) 1, sin( i ) i
и решать систему линейных уравнений
относительно
i
i 1
2 1 2 (Q1 P 1 )h 0,
2
i 1 2 i i 1 (Q P i )h 0, i 2,..., n 1
2 2 (Q P ) h 2 0, i n
n
n 1 n
2
.

47.

Решение уравнений в частных производных
Уравнения в частных производных используются при
моделировании разнообразных физических процессов:
задачи гидродинамики, исследование теплопроводности,
упругости и т.д.
Особенностью этих уравнений является отсутствие
универсального алгоритма их решения, для многих задач
требуется собственный особый подход к решению.

48. Решение уравнений в частных производных Уравнения в частных производных используются при моделировании разнообразных физических

Общий вид дифференциального уравнения 2–го
порядка с двумя независимыми переменными:
2u
2u
2u
u
u
a 2 2b
c 2 d
l
fu g
x y
x
y
x
y
• где u≡u(x,y), неизвестная функция, х и у – независимые
переменные.
• Дифференциальные уравнения в частных производных
имеют бесконечное множество решений.
• Чтобы получить единственное решение для конкретного
физического процесса, необходимо задать дополнительные
условия: начальные и краевые (граничные). Их вид и
количество зависит от типа уравнения.

49. Общий вид дифференциального уравнения 2–го порядка с двумя независимыми переменными:

ТИПЫ уравнений в частных производных
• Тип уравнения определяется по виду коэффициентов и
соотношениям между ними. Обычно рассматривают
уравнения трех основных типов: параболического (D =
b2–4ac=0); гиперболического (D>0); эллиптического
(D<0).
• Если все коэффициенты a, b, c, d, e, f, g не зависят от u, x,
y, то получается уравнение с постоянными
коэффициентами.
• Если g линейно зависит от u, а остальные коэффициенты
зависят только от x, y, уравнение называется линейным.
Если a = b = c = f, а d ≠ 0, e ≠0, то имеем уравнение 1–го
порядка.

50. ТИПЫ уравнений в частных производных

• Рассмотрим дифференциальное уравнение в
частных производных первого порядка:
u
u
a
f (t , x),
a 0
t
x
, u(t,x) – неизвестная функция двух независимых переменных t, x;
u(0,x)=φ(х) – начальное условие при t=0;
u(t,0)=ψ(t) – краевое условие при х=0.
Рассмотрим прямоугольную область: 0≤t≤Т
0≤х≤1. Строим
прямоугольную сетку: хj=jh, ti=iτ, i=0,1,2,…,n, j=0,1,…,m. Вместо
функций u(t,x), φ(х), ψ(t), f(t,х) будем рассматривать сеточные
функции uij, fij, φij, ψij.
Аппроксимируем производные по шаблону на рис.3. a).

51.

Уравнение Пуассона
2
2
u ( x, y ) u ( x, y )
f ( x, y )
2
2
x
y
• Это уравнение эллиптического типа, которое можно решить в
Mathcad с помощью встроенной функции
• Уравнение Пуассона описывает стационарное распределение
температуры u(x,t) на плоскости, в которой имеются источники тепла
с интенсивностью f(x,y).
• Область решения уравнения Пуассона должна иметь форму квадрата,
граничные условия задаются на всех сторонах квадрата. В самом
простом случае с нулевыми или постоянными граничными
условиями (постоянная температура на всей граничной области)
можно использовать встроенную функцию multigrid.

52. Уравнение Пуассона

• Функция multigrid (f, r) имеет два аргумента:
• f – имя матрицы, задающей правую часть уравнения; r – параметр
численного метода, обычно полагают r = 2. Количество точек
разбиения стороны квадрата m должно быть равно степени двойки: 4,
8, 16, и т.д. Графически функцию можно изобразить поверхностью,
выбрав на панели инструментов «построение поверхности» и указав в
шаблоне имя матрицы, содержащей значения неизвестной функции
u(x,y).

53.

Пример 2. Решить уравнение Пуассона, если при , m = 32 ,
имеются два источника тепла и один сток тепла.
Решение
m 32
f
m
4
3
m
4
f m m 0
2
f
3m m
4 4
s multigrid ( f 2)
1
f
m m
8 2
2

54. Пример 2. Решить уравнение Пуассона, если при , m = 32 , имеются два источника тепла и один сток тепла. Решение

Аппроксимация частных производных
u (t , x) функция двух переменных.
Пусть область решения заменена сеткой, узлы сетки имеют
координаты
(t i , x j )
(i,j) – целочисленные координаты узла.
При аппроксимации частных производных рассматривают
некоторую окрестность узла, называемую шаблоном.
Выбор шаблона обычно определяется конкретной задачей и
определенными требованиями к решению. Наиболее популярный
шаблон – так называемый «крест» ) и различные его подмножества.
шаг
шаг

55. Аппроксимация частных производных

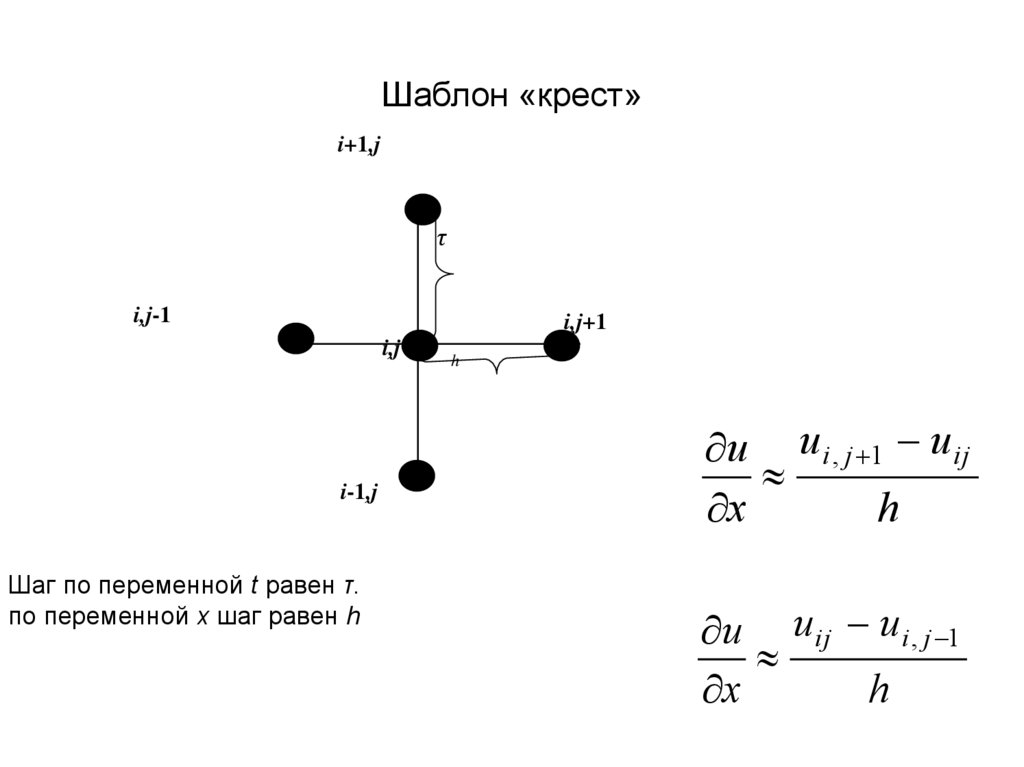
Шаблон «крест»
i+1,j
τ
i,j-1
i,j+1
i,j
i-1,j
Шаг по переменной t равен τ.
по переменной x шаг равен h
h
u u i , j 1 u ij
x
h
u u ij u i , j 1
x
h

56. Шаблон «крест»

;
• По этому шаблону частные
производные функции
;
в
узле
аппроксимировать
образом:
;
u ( x, t )
(i,j)
можно
следующим
u u i , j 1 2u ij u i , j 1 ;
x
2h
;
u u i 1, j u ij
t
u u ij u i 1, j
t
u u i 1, j 2u ij u i 1, j
t
2
;
2
u
2
x
u i , j 1 2u ij u i , j 1
h2
;
2 u u i 1, j 2u ij u i 1, j
2
t
2

57.

Дифференциальное уравнение в частных
производных первого порядка:
u
u
a
f (t , x),
t
x
a 0
,u(t,x) – неизвестная функция двух независимых переменных t, x;
u(0,x)=φ(х) – начальное условие при t=0;
u(t,0)=ψ(t) – краевое условие при х=0.
Рассмотрим прямоугольную область: 0≤t≤Т
0≤х≤1. Строим
прямоугольную сетку: хj=jh, ti=iτ, i=0,1,2,…,n, j=0,1,…,m. Вместо
функций u(t,x), φ(х), ψ(t), f(t,х) будем рассматривать сеточные
функции uij, fij, φij, ψij.

58. Дифференциальное уравнение в частных производных первого порядка:

i+1,j
τ
i,j-1
h
i,j
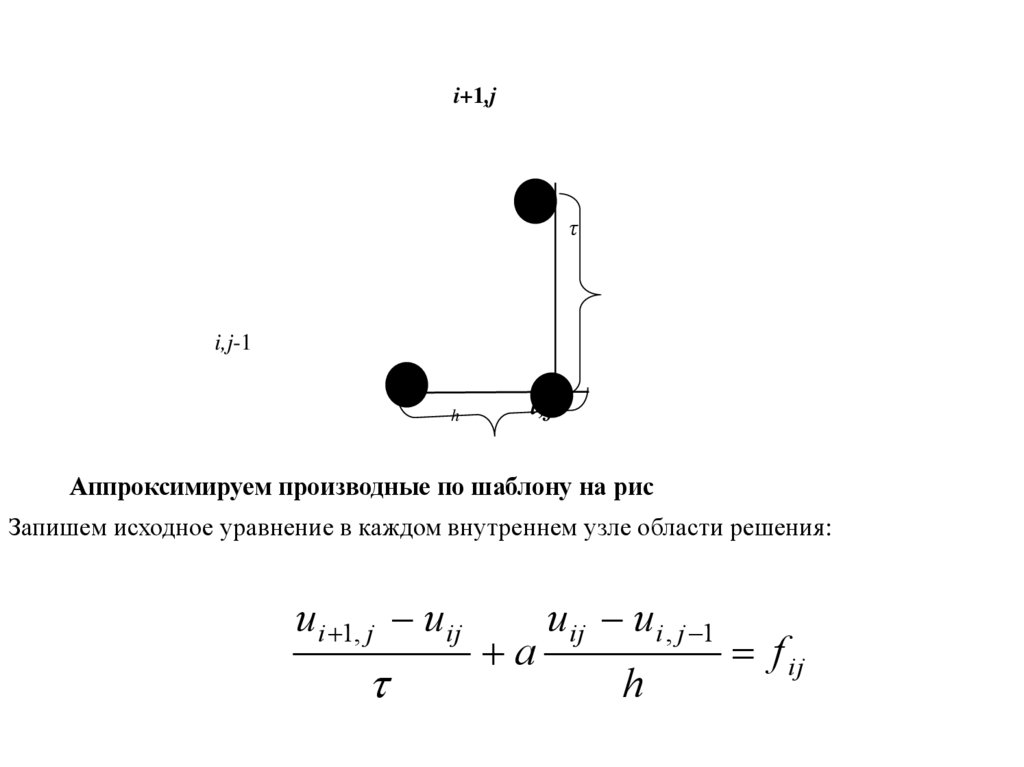
Аппроксимируем производные по шаблону на рис
Запишем исходное уравнение в каждом внутреннем узле области решения:
u i 1, j u ij
a
u ij u i , j 1
h
f ij

59.

• Отсюда
a
a
u i 1, j
u i , j 1 1
u ij f ij
h
h
где i=0,1,2,…,n; j=0,1,2,…, m
Вычисления идут по слоям. На нулевом слое u0j=φj (φi
вычисляется как φ(xj)), ui0=ψ(ti).
Получилась явная разностная схема: значения сеточной
функции в каждом узле верхнего слоя вычисляются
через значения на предыдущем слое.

60.

• Схема устойчива при 0≤τ≤h/a, при этом u(t,x), φ(х),
ψ(t) должны быть дважды непрерывно
дифференцируемы; f(х,t) имеет непрерывные первые
производные. Сеточное решение сходится к точному
при h→0; τ→0. При а<0 условие устойчивости не
выполняется, и схема не сходится.
• При а<0 сходящаяся разностная схема
получается при использовании шаблона,
показанного на рис.
i+1,j
u i 1, j u ij
τ
i,j+1
i,j
a
u i , j 1 u ij
h
f ij
h
Эта схема устойчива при а<0, если выполнено условие τ≤–h/a. При
а>0 эта схема не сходится.

61.

i+1,j
i,j-1
τ
h
i,j
При использовании шаблона, изображенного на рис, получается неявная
разностная схема. Вычисления можно вести по слоям, как в явной схеме.
Эта схема безусловно устойчива, т.е. не накладывается никаких условий
на соотношения между шагами при аппроксимации производных
a
a
u i 1, j (1
) u ij u i 1, j 1
f ij
h
h
a
f ij u ij u i 1, j 1
h
u i 1, j
a
1
h

62.

• Пример.
u
u
3 xt
t
x
u( x,0) x, u(0, t ) t , 0 x 1, 0 t 1

63.

Уравнение колебания струны
• Рассмотрим одномерное волновое уравнение,
которое описывает, например, свободное
колебание струны из исходного неравновесного
положения. Такое движение можно наблюдать,
если закрепленную с двух концов струну оттянуть
из прямолинейного положения и отпустить в
свободные от дальнейшего силового воздействия
колебания.

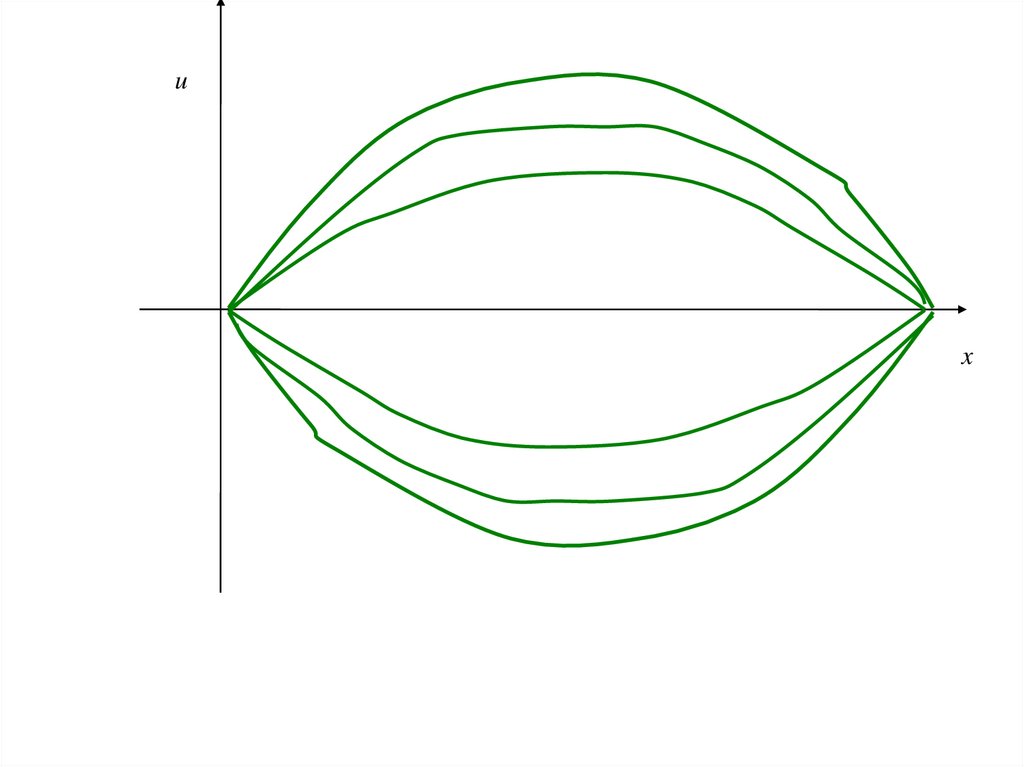
64.

u
x

65.

Динамику смещения профиля струны относительно
прямолинейного положения описывает волновое уравнение
2
:
2
u
2 u
c
2
2
x
t
u ( x, t ) – поперечное смещение точки струны с координатой в момент времени t,
c – константа для материала, из которого изготовлена струна.
Условия закрепления концов струны длиной (краевые условия):
u(0, t) = u(l, t) = 0. Начальные условия задают форму струны в
начальный момент времени: u(x, 0) = f(x), а исходное распределение
скоростей запишется как
u ( x,0)
g ( x)
t