Моделирование систем. Классификация моделей

1. Моделирование систем

Лекция 1
1

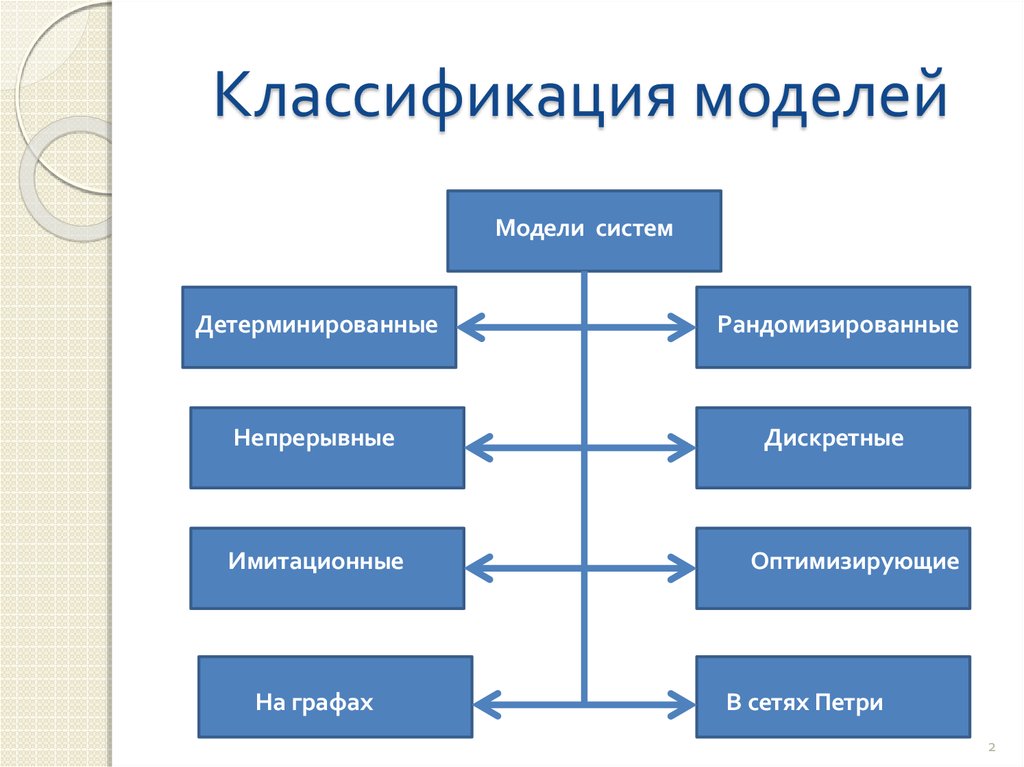
2. Классификация моделей

Модели систем
Детерминированные
Рандомизированные
Непрерывные
Дискретные
Имитационные
На графах
н На графа
Оптимизирующие
В сетях Петри
2

3. Детерминированная модель с непрерывно меняющимися переменными

Определить оптимальный портфель заказов предприятия:
xi ci max;
i
j : xi ai , j b j ;
i
i : xi 0,
где: хi – объем выпускаемой продукции i-го вида; сi – стоимость
единицы выпускаемой продукции i-го вида; b – ресурс сырья j-го
вида; а – затраты сырья j-го вида на единицу продукции i-го вида.
Самостоятельно:
1.
Обобщить модель на случай нескольких предприятий.
2.
Выбрать алгоритм решения задачи в общем случае.
3.
Определить эффективный алгоритм для случая, когда
величина j не превосходит единицы.
j
i,j
3

4. Детерминированная модель с дискретно меняющимися переменными

Определить оптимальный портфель заказов предприятия:
xi ci max;
i
j : xi ai , j b j ;
i
i : xi 1,0,
где: х = 1 если i-й наряд-заказ принят и х = 0, если он
отвергнут; с – стоимость i-го наряд-заказа; b – ресурс сырья
j-го вида; а – затраты сырья j-го вида на выполнение i-го
наряд-заказа.
Самостоятельно:
1.
Обобщить модель на случай нескольких предприятий.
2.
Выбрать алгоритм решения задачи.
3.
Выделить отличия от задачи о ранце.
i
i
i
j
i,j
4

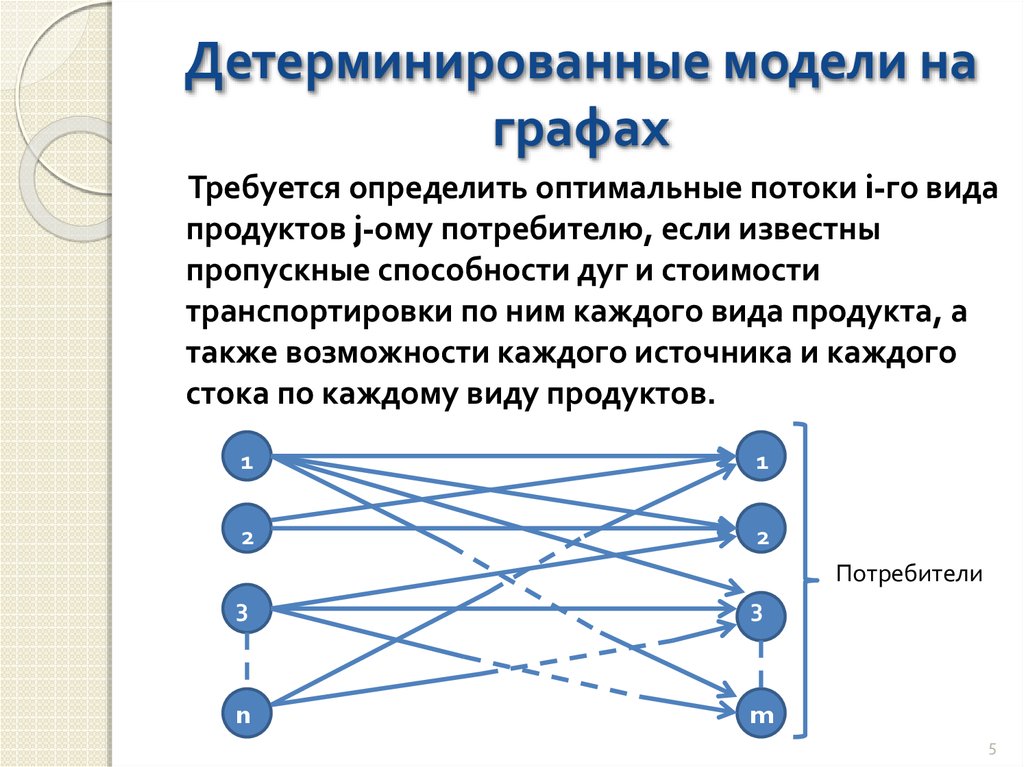
5. Детерминированные модели на графах

Требуется определить оптимальные потоки i-го вида
продуктов j-ому потребителю, если известны
пропускные способности дуг и стоимости
транспортировки по ним каждого вида продукта, а
также возможности каждого источника и каждого
стока по каждому виду продуктов.
1
1
2
2
Потребители
3
3
n
m
5

6. Формальная постановка задачи

Случай, когда конкуренция между производителями отсутствует
xi , j ci , j min;
i j
2
x
b
i , j i , j min;
i j
i : xi , j ai ;
j
(i, j ) U : 0 xi , j ri , j ,
где: xi,j - поток i-го продукта j-у потребителю; аi – производственная
мощность производителя i-го продукта; bj ,j- потребность j-го потребителя в
i-м продукте; сi,j – стоимость транспортировки единицы i-го вида продукта jму потребителю; ri,j – пропускная способность дуги (i,j).
Самостоятельно:
1. Свести задачу к однокритериальной.
2. Определить алгоритм решения задачи.
3. Дать формальную постановку задачи при наличии конкуренции
среди производителей.
6

7. Имитационные модели переменных процессов на базе дифференциальных уравнений.

Изолированный остров населен:
1) мхами (Х1),
dx 2 GX
2) оленями (X2),
2;
dt dx
KX
3) волками (X3 ).
dt
Количество мха зависит от времени года и количества оленей
Х1=А+Вsin t – GX2;
X2 – количество оленей.
Х2=СХ1 – DX3 – пропорционально количеству мха.
Прирост оленей пропорционален количеству оленей.
X3=HX2 – количество волков пропорционально количеству оленей.
Самостоятельно:
1.
Построить модель жизни острова.
2.
Исследовать построенную модель и определить параметры, при
которых имеет место стабильный симбиоз.
3
3
7

8. Дискретно-непрерывная модель

Эпидемия. Обозначения:
Х(i) – число заболевших в i-й день.
Т – время через которое болезнь проходит.
t – текущее время в днях.
k – коэффициент, показывающий сколько
человек в среднем заражает один больной.
Y(t) – число выздоровевших в t-ый день.
Z(t) – число умерших в t-ый день.
8

9. Дискретно-непрерывная модель эпидемии

X(i+1)=X(i)+kX(i) – количество людей, заболевших в i+1
день.
X(i-T)=Y(i)+Z(i) для любого i>T.
где:
0, если i<T
Y(i)=
f(X(i-T)), если i > T
0, если i<T;
Xi
Yi
Zi
i
10
0
0
1
40
0
0
2
160
0
0
3
600
9
1
4
2240
36
4
5
8320
144
16
6
…
…
…
7
Z(i)=
X(i-T) – f (X(i-T)), при i > T
9

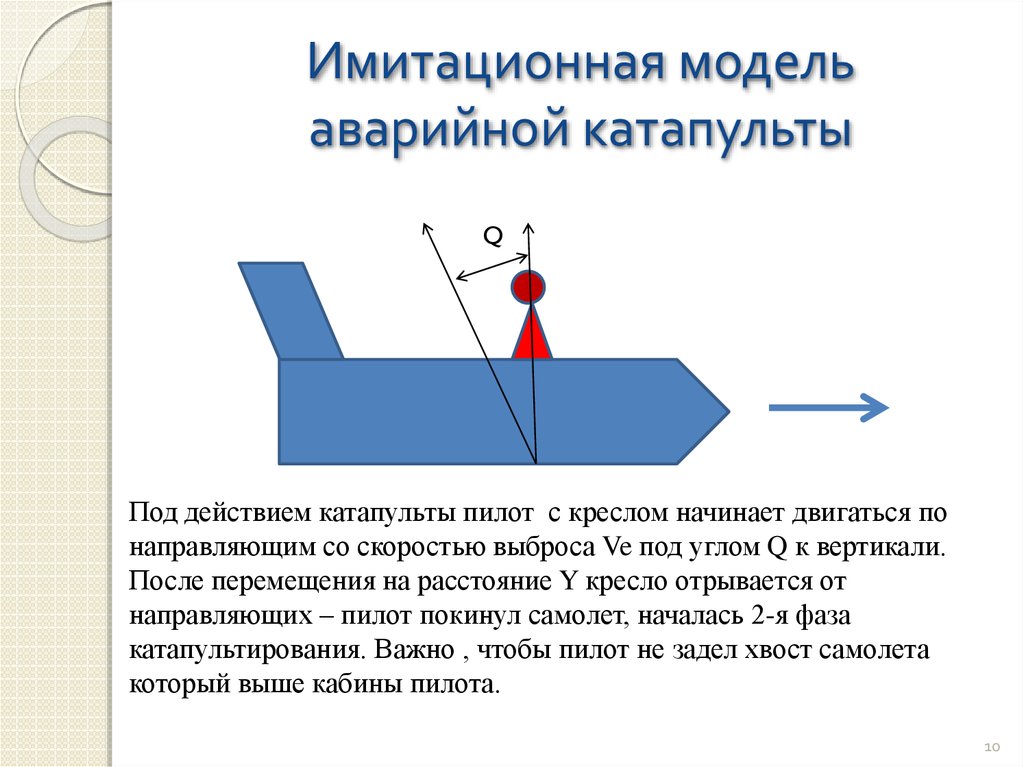
10. Имитационная модель аварийной катапульты

Q
Под действием катапульты пилот с креслом начинает двигаться по
направляющим со скоростью выброса Ve под углом Q к вертикали.
После перемещения на расстояние Y кресло отрывается от
направляющих – пилот покинул самолет, началась 2-я фаза
катапультирования. Важно , чтобы пилот не задел хвост самолета
который выше кабины пилота.
10

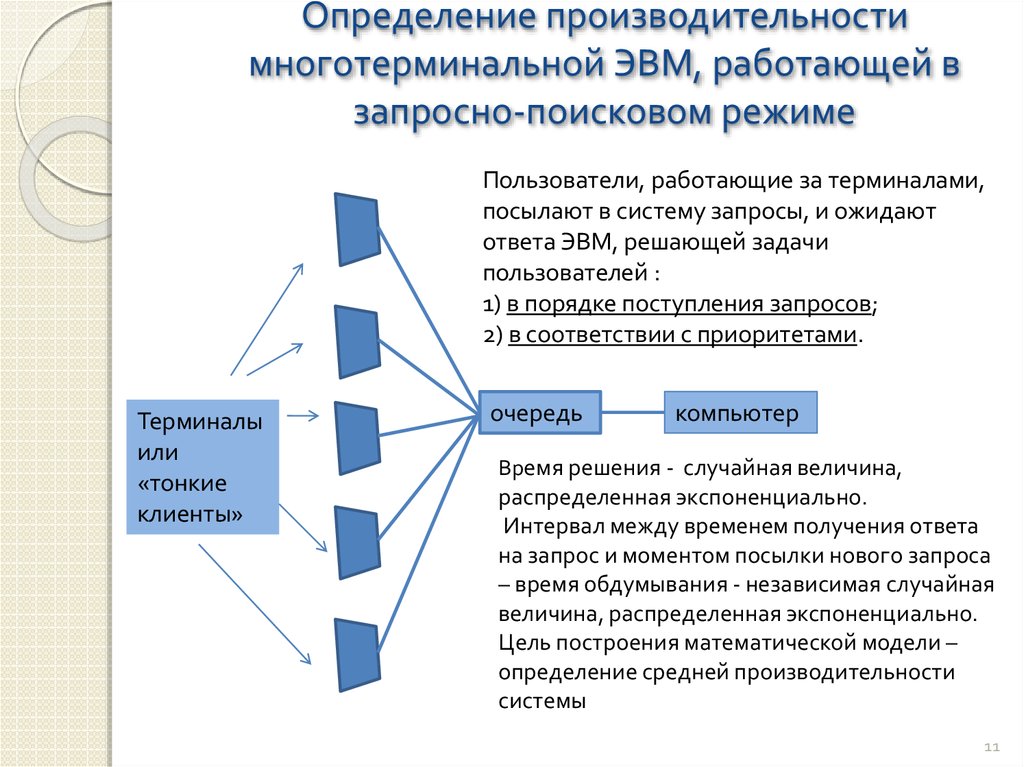
11. Определение производительности многотерминальной ЭВМ, работающей в запросно-поисковом режиме

Пользователи, работающие за терминалами,
посылают в систему запросы, и ожидают
ответа ЭВМ, решающей задачи
пользователей :
1) в порядке поступления запросов;
2) в соответствии с приоритетами.
Терминалы
или
«тонкие
клиенты»
очередь
компьютер
Время решения - случайная величина,
распределенная экспоненциально.
Интервал между временем получения ответа
на запрос и моментом посылки нового запроса
– время обдумывания - независимая случайная
величина, распределенная экспоненциально.
Цель построения математической модели –
определение средней производительности
системы
11

12. Использование сетей Петри в моделях формирования выходных документов автоматизированных систем управления предприятиями – содержатель

Использование сетей Петри в моделях формирования
выходных документов автоматизированных систем
управления предприятиями – содержательная
постановка задачи
Задано множество документов, которые
нужно формировать на основе базы данных
и множества программных единиц, которые
могут это делать. Каждая единица
характеризуется временем и объемом
памяти. Каждый документ характеризуется
объемом используемой памяти. Требуется
построить такую стратегию формирования
документов, которая бы:
Минимизировала время формирования
выходных документов.
Удовлетворяло ограничениям на объем
используемой памяти.
12

13. Использование сетей Петри в моделях формирования выходных документов автоматизированных систем управления предприятиями – визуальное п

Использование сетей Петри в моделях формирования
выходных документов автоматизированных систем
управления предприятиями – визуальное представление
задачи
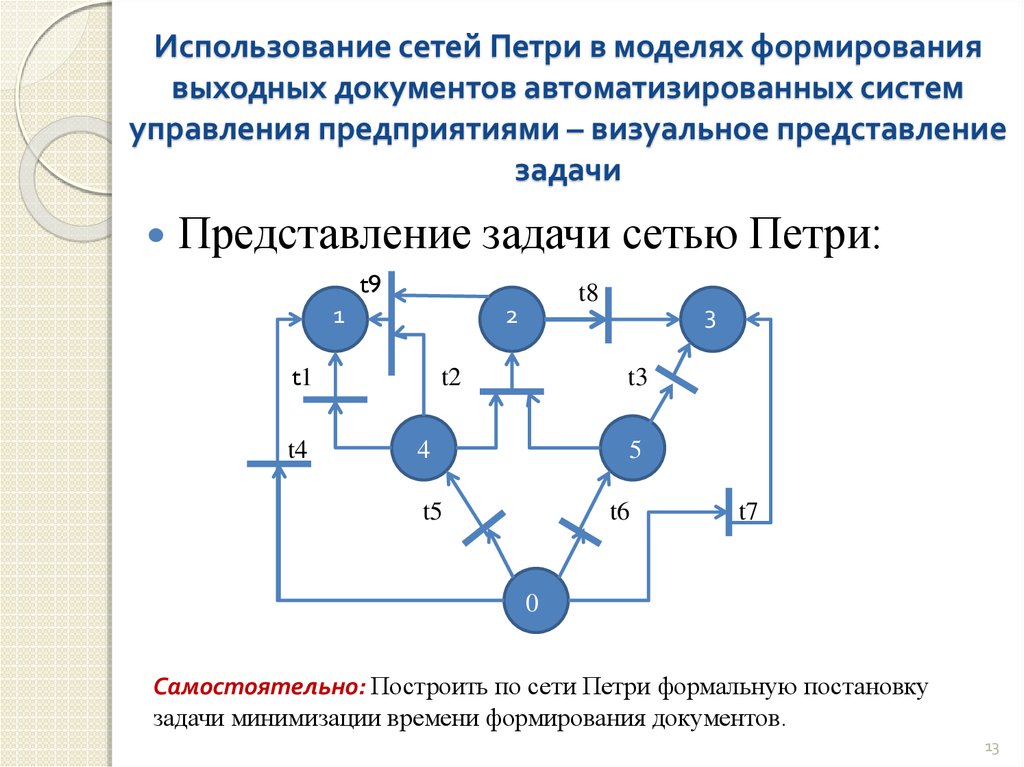
Представление задачи сетью Петри:
t9
1
t1
t4
t8
2
t2
3
t3
4
5
t5
t6
t7
0
Самостоятельно: Построить по сети Петри формальную постановку
задачи минимизации времени формирования документов.
13

14. Математическое моделирование процессов в астрофизике

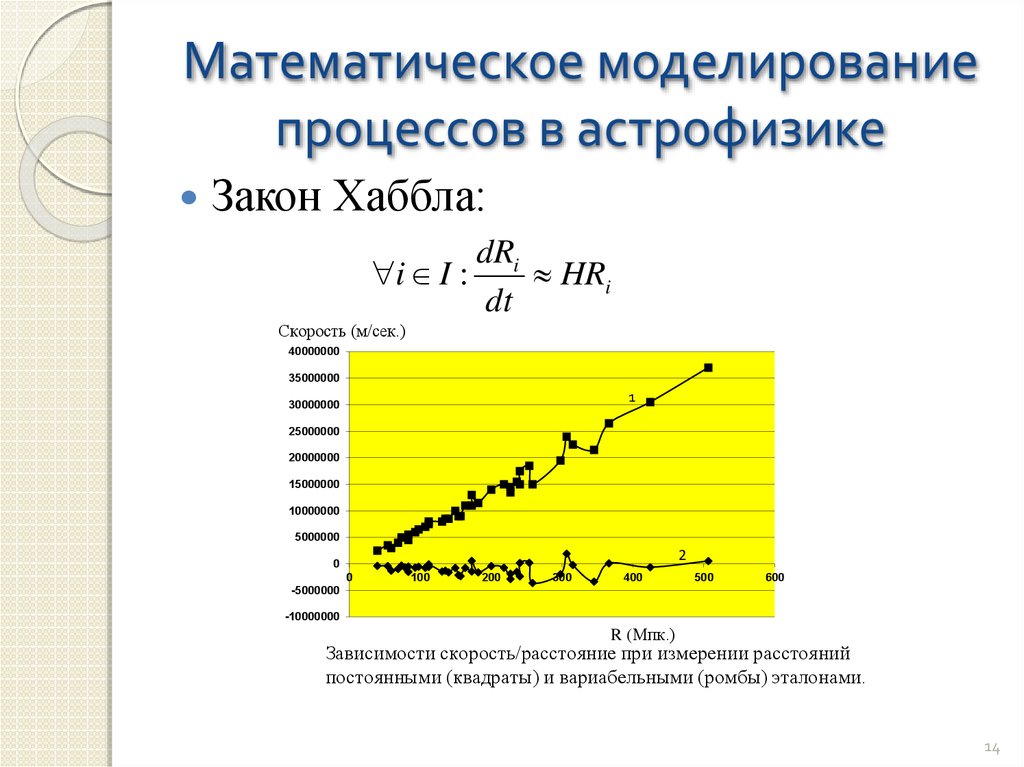
Закон Хаббла:
dRi
i I :
HRi
dt
Скорость (м/сек.)
40000000
35000000
1
30000000
25000000
20000000
15000000
10000000
5000000
2
0
0
100
200
300
400
500
600
-5000000
-10000000
R (Мпк.)
Зависимости скорость/расстояние при измерении расстояний
постоянными (квадраты) и вариабельными (ромбы) эталонами.
14

15. Математическое моделирование процессов в ядерной физике

H
D
T
He
N
P
P
N
P
N
He
3
N
P
4
N
P
P
P
N
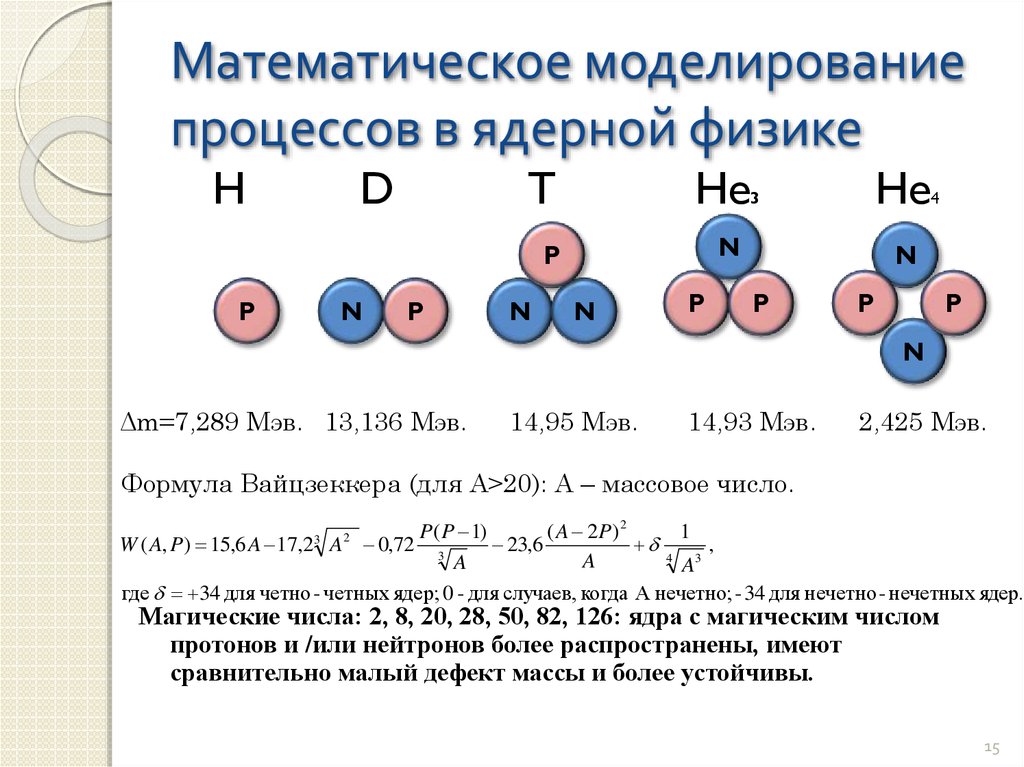
Δm=7,289 Мэв. 13,136 Мэв.
14,95 Мэв.
14,93 Мэв.
2,425 Мэв.
Формула Вайцзеккера (для А>20): А – массовое число.
P( P 1)
( A 2 P) 2
1
W ( A, P) 15,6 A 17,2 A 0,72 3
23,6
,
3
4
A
A
A
где 34 для четно - четных яде р; 0 - для случаев, когда А нечетно; - 34 для нечетно - нечетных ядер.
3
2
Магические числа: 2, 8, 20, 28, 50, 82, 126: ядра с магическим числом
протонов и /или нейтронов более распространены, имеют
сравнительно малый дефект массы и более устойчивы.
15

16. Графическая иллюстрация

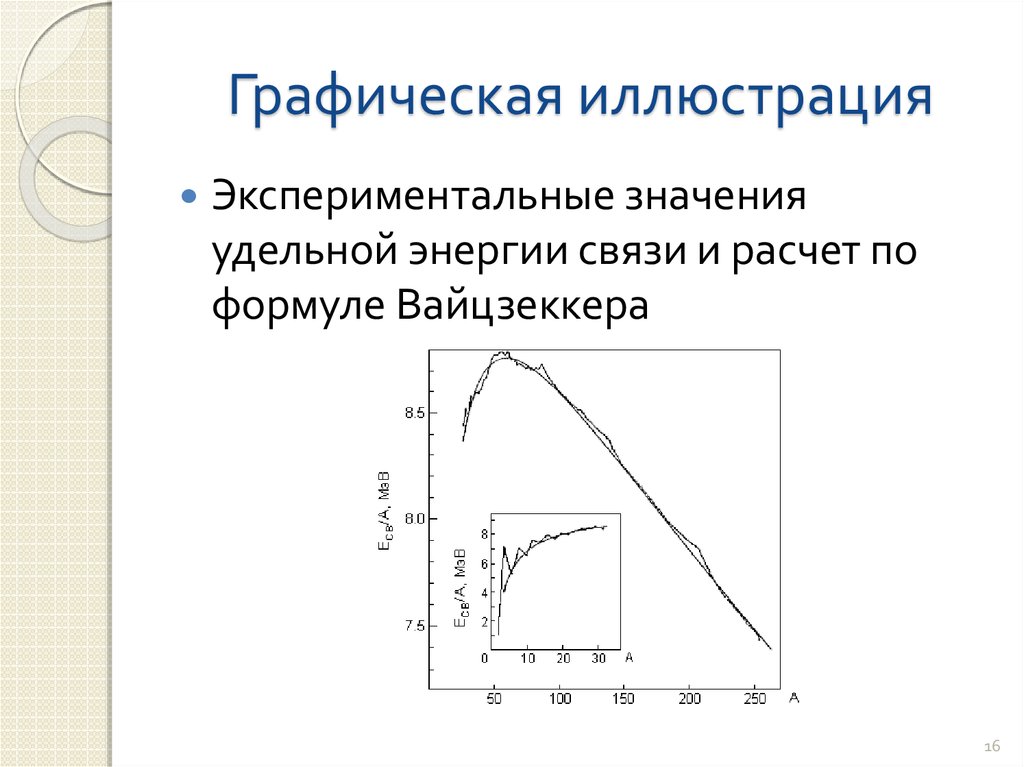
Экспериментальные значения
удельной энергии связи и расчет по
формуле Вайцзеккера
16

17. Самостоятельно

Решить приведенную ниже задачу:
1. Симплекс методом;
2. Предложить свой метод решения.
3. Результаты сравнить.
xi ci max;
i
i : xi ai bi ;
i : x 0.
i
17