Similar presentations:
Математический анализ. Определенный интеграл
1. МАТЕМАТИЧЕСКИЙ АНАЛИЗ
2 семестр1
2. ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ
• Даны:- отрезок [a,b],
- неотрицательная функция f(x)
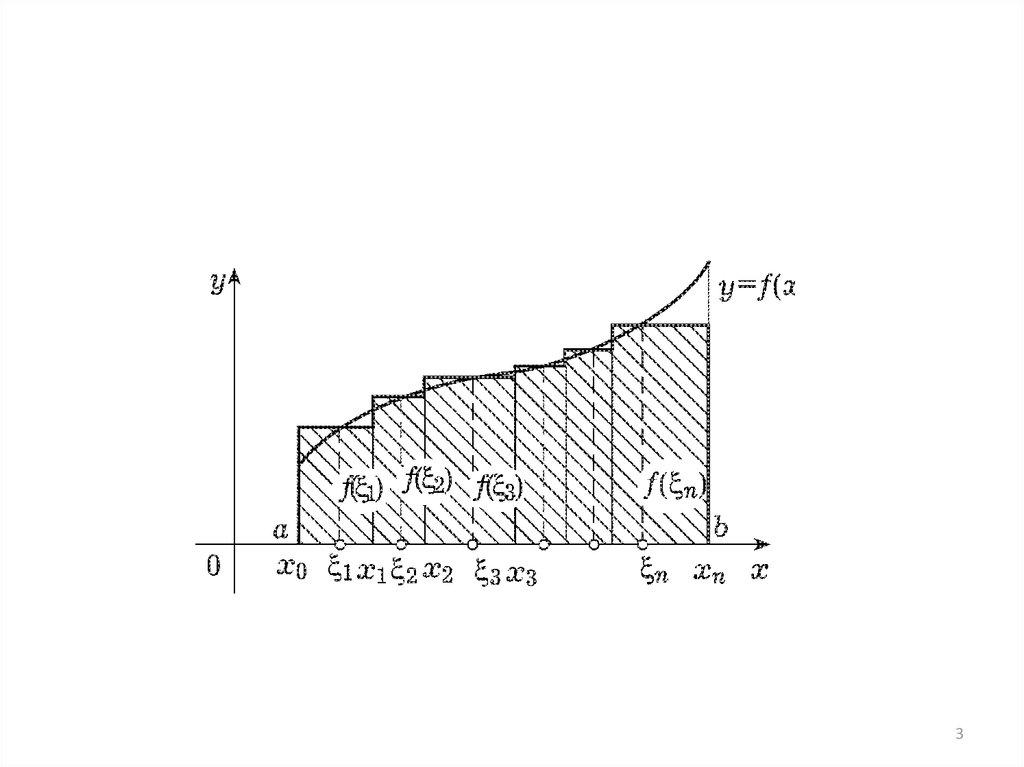
Криволинейная трапеция
Площадь?
2
3.
34.
• 4 шага:1. Разбить отрезок.
2. Выбрать точки.
3. Интегральная сумма.
4. Перейти к пределу.
4
5.
1. a=x0<x1<…<xn=b,xi=xi xi 1 (i=1,2,…,n)
2. 1 [x0,x1], 2 [x1,x2],…, n [xn 1,xn]
3. Интегральная сумма
f( 1) x1+ f( 2) x2+…+f( n) xn
5
6.
• 4. =max{ xi}• ОПРЕДЕЛЕНИЕ 1. Если предел
интегральных сумм
6
7.
при 0 существует, то он называетсяопределенным интегралом от функции f(x)
по отрезку [a,b], обозначается
b
f ( x)dx
a
В этом случае функция f(x) называется
интегрируемой на отрезке [a,b].
7
8.
• Особенность предела!• Пример интегрируемой функции: f(x)=с.
• Замечание. Если функция интегрируемая,
то она ограниченная. Обратное неверно
(функция Дирихле)
8
9.
• Много ли интегрируемых функций?ТЕОРЕМА 1. Если функция f(x) непрерывна
на отрезке [a,b], то она
интегрируема на этом отрезке
ТЕОРЕМА 2. Монотонная ограниченная
функция является интегрируемой.
.
9
10. СВОЙСТВА ОПРЕДЕЛЕННОГО ИНТЕГРАЛА
af ( x)dx 0
• 1. (договоренность)
a
• 2. (договоренность)
b
a
a
b
f ( x)dx f ( x)dx
10
11.
3. (линейность) Если функции f(x) и g(x)интегрируемы на [a,b], то функция
сf(x)+dg(x) также интегрируема на [a,b],
причем
b
b
b
a
a
a
cf ( x) dg ( x) dx c f ( x)dx d g ( x)dx
11
12.
4. Произведение интегрируемых функцийинтегрируемая функция. ФОРМУЛЫ ДЛЯ
ВЫЧИСЛЕНИЯ ИНТЕГРАЛА
ПРОИЗВЕДЕНИЯ НЕ СУЩЕСТВУЕТ!
5. Если функция f(x) интегрируема на [a,b], то
она интегрируема и на [с,d] [a,b].
12
13.
6. (аддитивность) Если функция f(x)интегрируема на [a,c] и [c,b] , то она
интегрируема и на [a,b]. При этом
b
c
b
a
a
c
f ( x)dx f ( x)dx f ( x)dx
Формула справедлива при любом
расположении точек a, b, c
13
14. ОЦЕНКИ ИНТЕГРАЛОВ
1. Если f(x) 0 на [a,b] и интегрируемая, тоb
f ( x)dx 0.
a
2. Если f(x) m на [a,b] и интегрируемая, то
b
f ( x)dx m(b a).
a
14
15.
3. Если непрерывная функция f(x) 0 на [a,b] иf(x)>0 в некоторой точке, то
b
f ( x)dx 0.
a
4. Если f(x) и g(x) интегрируемые на [a,b] и
f(x) g(x), то
b
b
a
a
f ( x)dx g ( x)dx
15
16.
5. Если функция f(x) интегрируемая на [a,b],то |f(x)| также интегрируема и
16
17.
6. Пусть f(x) и g(x) интегрируемые на [a,b],f(x) 0 и m g(x) M. Тогда
b
b
b
a
a
a
m f ( x)dx f ( x) g ( x)dx M f ( x)dx
17
18.
• ТЕОРЕМА 3 (о среднем значении).Пусть f(x) интегрируемая на [a,b]
и m f(x) M.
Существует число [m,M], для которого
b
f ( x)dx (b a)
a
Геометрический смысл
18
19.
• СЛЕДСТВИЕ. Если дополнительно функцияf(x) непрерывна на [a,b], то существует
число [a,b], для которого
b
f ( x)dx f ( )(b a)
a
19
20. ИНТЕГРАЛ С ПЕРЕМЕННЫМ ВЕРХНИМ ПРЕДЕЛОМ
xF ( x) f (t )dt
a
20
21.
ТЕОРЕМА 4. Функция F(x) непрерывная.ТЕОРЕМА 5. Если функция f(x) непрерывная,
то функция F(x) дифференцируемая,
причем F (x)=f(x).
21
22.
• СЛЕДСТВИЕ. (Формула Ньютона-Лейбница)• Если функция f(x) непрерывная на [a,b] и
(x) – первообразная f(x), то
b
f (t )dt (b) (a)
a
22
23.
a=0, b= /223
24. ЗАМЕНА ПЕРЕМЕННЫХ В ОПРЕДЕЛЕННОМ ИНТЕГРАЛЕ
ТЕОРЕМА 6. ПустьТогда
24
25.
• ПРИМЕРЫ• 1.
• 2.
25
26.
• ИНТЕГРИРОВАНИЕ ПО ЧАСТЯМ• ТЕОРЕМА 7. Пусть функции u(x), v(x) имеют
непрерывные производные на отрезке [a,b].
Тогда
26
27.
• ПРИМЕРЫ27
28. ПРИЛОЖЕНИЯ ОПРЕДЕЛЕННОГО ИНТЕГРАЛА
1. Длина дуги кривойt - параметр
Функции непрерывные!
Если разным значениям параметра
соответствуют разные точки плоскости, то
дуга называется простой.
28
29.
• ЗАМЕЧАНИЯ• 1. Входят кривые, заданные уравнениями
y=f(x).
2. Параметр не единственный!
Непрерывная монотонная функция u(t), u –
тоже параметр
29
30.
• Строфоида• Простые дуги на множествах t<0, t>0
30
31.
• Пространственные кривые• Пример
• x=r sin t, y=r cos t, z=ct
31
32.
• Длина дуги. Диагональ квадрата• Вписанная ломаная x= (t), y= (t)
32
33.
• Шаг разбиения =max{ ti}• ОПРЕДЕЛЕНИЕ 2. Предел длин вписанных
ломаных при 0, если он существует,
называется длиной дуги, дуга в этом случае
называется спрямляемой.
33
34.
• ТЕОРЕМА 8 (Достаточные условияспрямляемости. Вычисление длины дуги)
• Пусть функции x= (t), y= (t) имеют
непрерывные производные на отрезке [ , ].
• Тогда дуга спрямляемая, ее длина
l
x (t ) y (t )
2
2
dt
• Для дуги пространственной кривой аналогично
34
35.
1. Если дуга спрямляемая, то длина независит от параметризации непрерывно
дифференцируемой функцией.
2. Если спрямляемая кривая разбита на
части, то каждая часть спрямляемая и
длина всей дуги равна сумме длин частей.
3. Пусть l=l(t) – длина дуги кривой от до t.
l – параметр (натуральный)
35
36.
• Для кривой y=f(x)• Для кривой, заданной в полярных
координатах уравнением r( ) ( 1 2)
36
37.
• Дифференциал дуги• Для пространственной кривой
37
38.
• Примеры вычисления длины дуги.• 1. Циклоида
• 2. Цепная линия
[0,a]
• 3. Длина дуги эллипса
38
39. ПЛОШАДЬ ПЛОСКИХ ФИГУР
• 1. Криволинейная трапеция39
40.
• 2. Криволинейный сектор40
41.
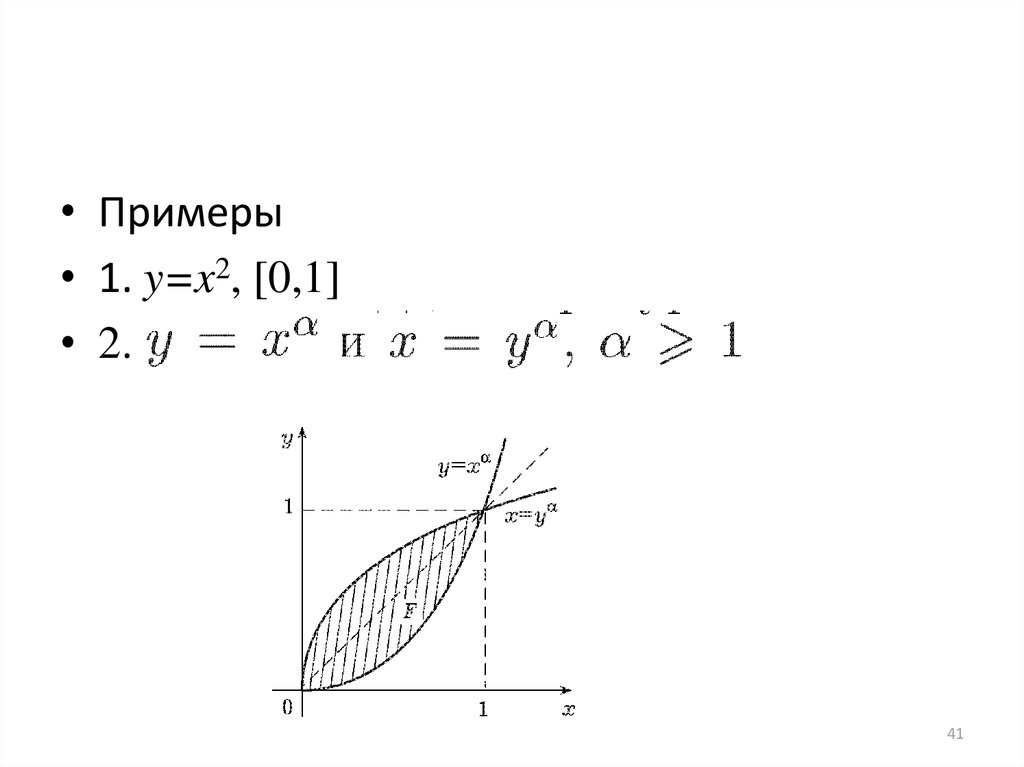
• Примеры• 1. y=x2, [0,1]
• 2.
41
42.
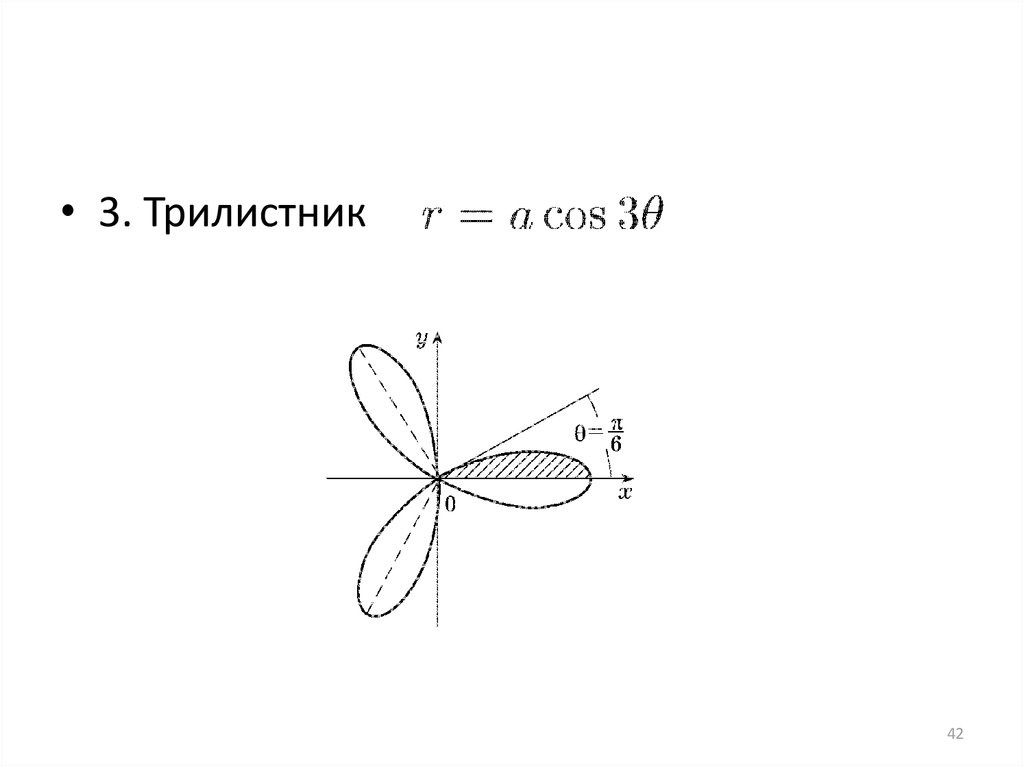
• 3. Трилистник42
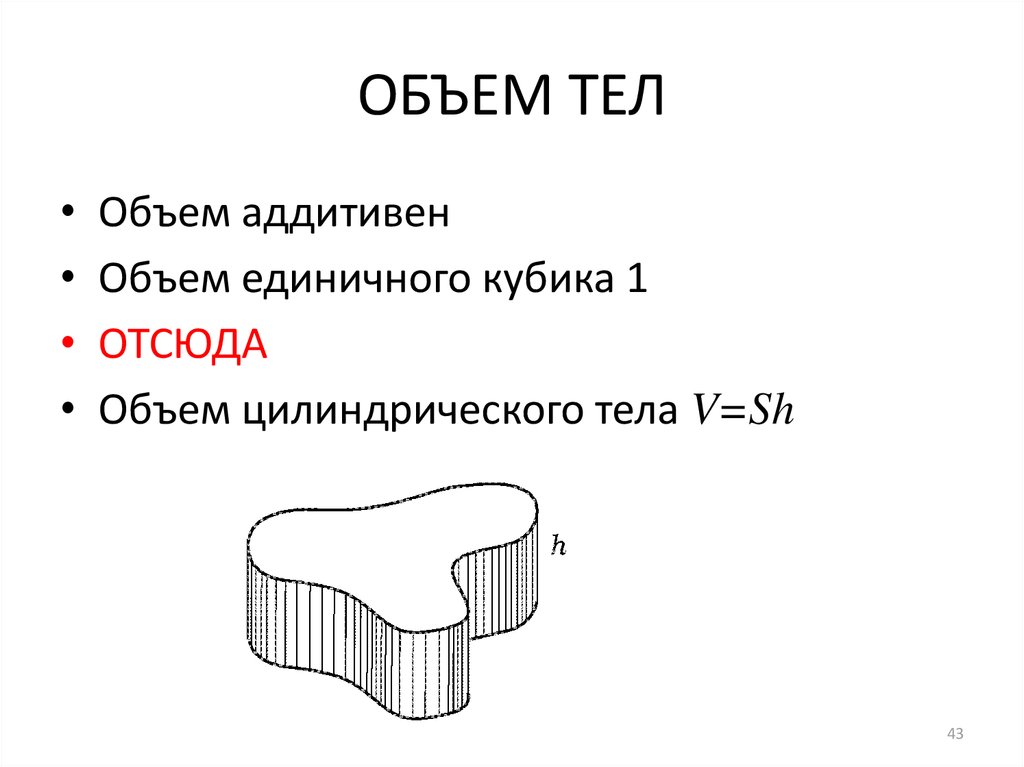
43. ОБЪЕМ ТЕЛ
Объем аддитивен
Объем единичного кубика 1
ОТСЮДА
Объем цилиндрического тела V=Sh
43
44.
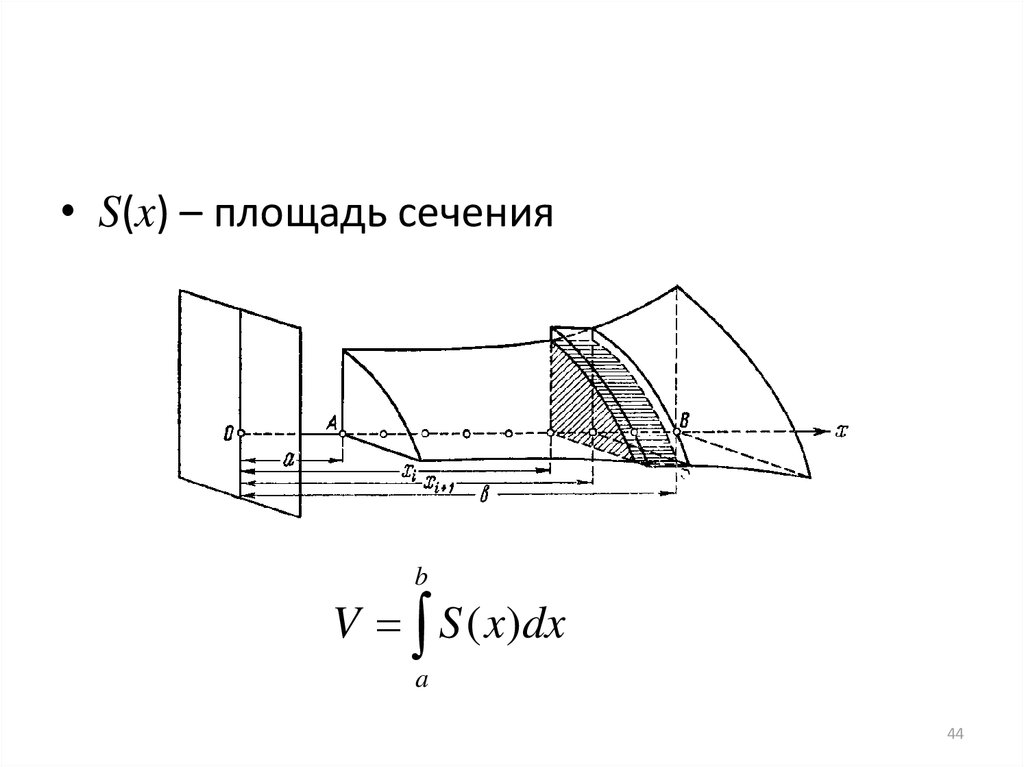
• S(x) – площадь сеченияb
V S ( x)dx
a
44
45.
• Объем тела вращения• Криволинейная трапеция
a x b, 0 y f(x), f(x) – непрерывная функция
Тело получено вращением трапеции вокруг
оси абсцисс
b
V f ( x)dx
2
a
45
46.
• ПРИМЕРЫ• 1. y=sin x на [0, ]
• 2. Астроида
46
47.
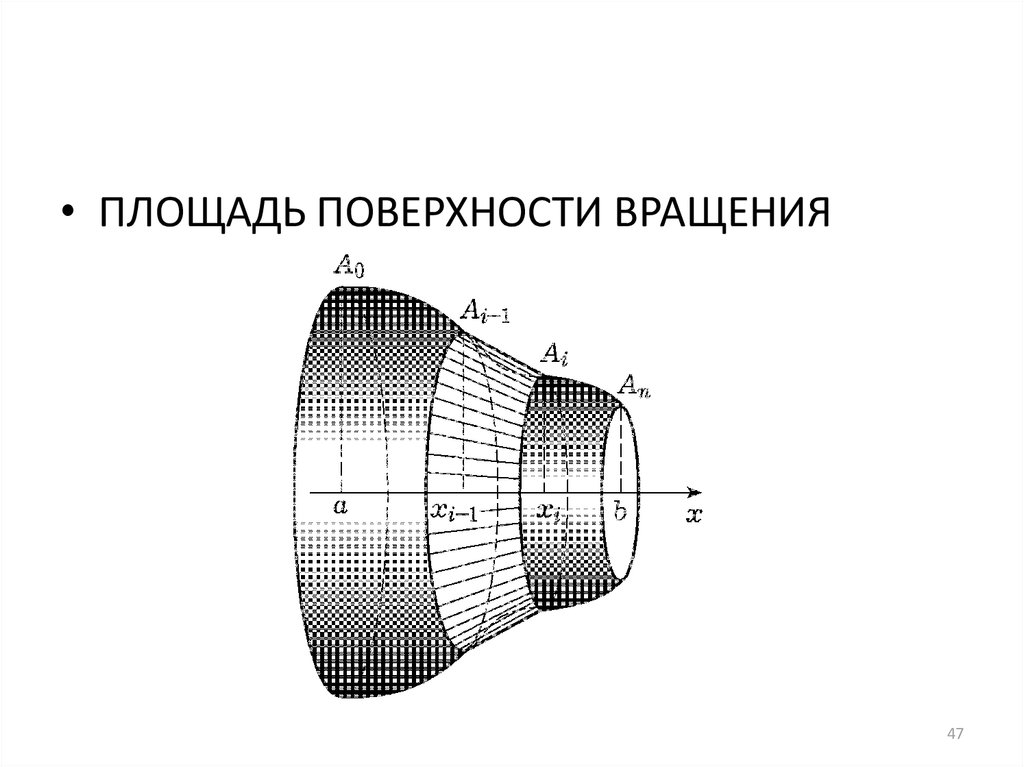
• ПЛОЩАДЬ ПОВЕРХНОСТИ ВРАЩЕНИЯ47
48.
• Площадь боковой поверхности коническоготела
n
P( xi ) yi 1 yi li
i 1
• li=
48
49.
• ОПРЕДЕЛЕНИЕ 3. Площадью поверхностивращения называется
P lim 0 P( xi )
=max{ xi}
49
50.
• При параметрическом задании50
51.
• ПРИМЕРЫ• 1.
• 2. Циклоида
51
52. НЕСОБСТВЕННЫЕ ИНТЕГРАЛЫ
• Обобщение интеграла на бесконечныепромежутки и неограниченные функции
• 1 рода
• Пусть функция f(x)
- определена на [a, )
- интегрируемая на [a,b]
52
53.
• ОПРЕДЕЛЕНИЕ 4. Несобственныминтегралом 1 рода называется
a
b
f ( x)dx limb f ( x)dx.
a
• Если предел не существует, то интеграл
расходится
53
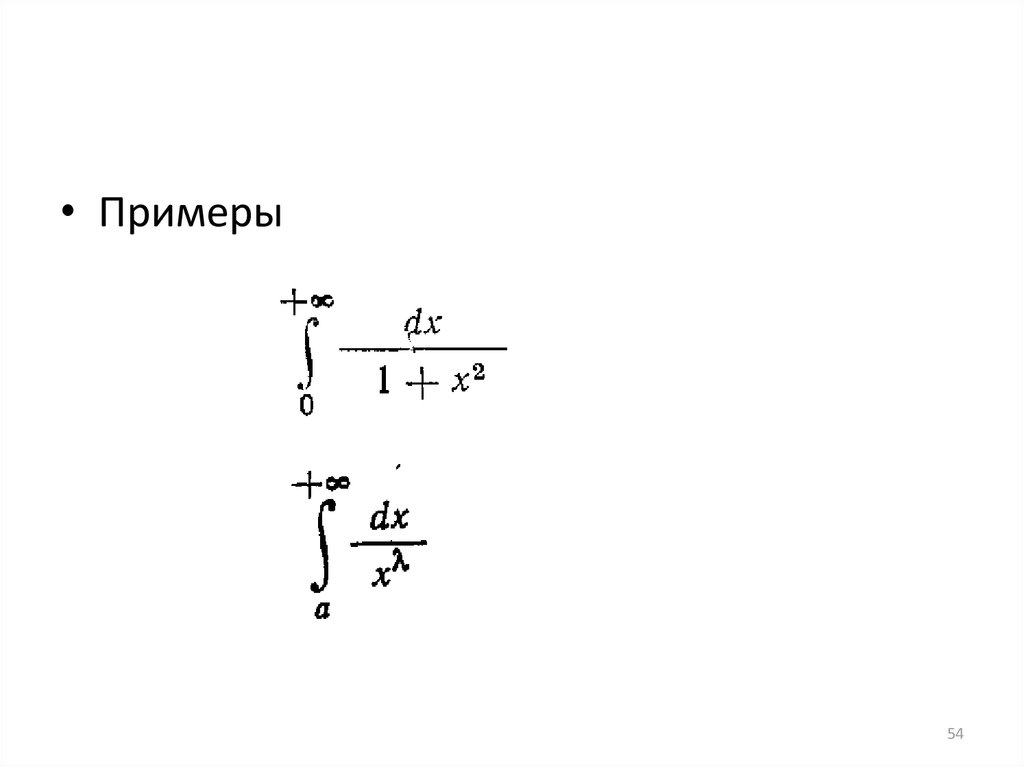
54.
• Примеры54
55.
• Аналогичноa
a
f ( x)dx limb f ( x)dx.
b
• Если f(x) непрерывна на всей прямой, то
a
f ( x)dx
f ( x)dx f ( x)dx.
a
55
56.
• Достаточное условие сходимости НИ 1 рода• ТЕОРЕМА 9. Если f(x) 0, интегрируема на [a,b]
при любом b>a и b
f ( x)dx M ,
то
a
f ( x)dx
a
сходится.
56
57. НЕСОБСТВЕННЫЕ ИНТЕГРАЛЫ 2 РОДА
5758.
ОПРЕДЕЛЕНИЕ 5. Несобственным интегралом 2рода называется
Обозначение
b
f ( x)dx
a
Если предел не существует, то интеграл
расходится.
58
59.
• Аналогично, если особая точка – левыйконец промежутка.
• ПРИМЕР.
1
dx
0 x
59
60. ЧИСЛОВЫЕ РЯДЫ
• Числовая последовательностьu1 , u2 ,..., un ,...
• ОПРЕДЕЛЕНИЕ 6. Числовым рядом
называется символ
u1 u2 ... un ... ui
i 1
60
61.
• Частичные суммыn
Sn u1 u2 ... un ui
i 1
• ОПРЕДЕЛЕНИЕ 7. Числовой ряд сходится,
если существует S lim Sn .
S – сумма ряда
Если предел не существует, то ряд
расходится.
61
62.
• ПРИМЕРЫ• 1.
1 1+1 1+…
• 2.
• 3.
62
63.
• ТЕОРЕМА 10 (необходимый признаксходимости ряда).
• Если ряд
u
i 1
i
сходится, то ui 0.
• ПРИМЕР.
63
64.
• ЗАМЕЧАНИЯ.• 1.
• 3.Сумма сходящихся рядов сходящийся ряд.
64
65. РЯДЫ С ПОЛОЖИТЕЛЬНЫМИ ЧЛЕНАМИ
• ТЕОРЕМА 11. Для сходимости ряда с положительными членаминеобходимо и достаточно, чтобы его частичные суммы были
ограничены.
• ТЕОРЕМА 12. (признак сравнения) Пусть
u и u i 1
i
i 1
i
ряды с положительными членами, причем
Если сходится ряд
i ui ui .
u , то сходится и ряд u
i
i 1
i 1
Если расходится ряд
u
i 1
i
, то расходится и ряд
i
u
i 1
i
65
66.
• ЗАМЕЧАНИЯ.1. То же самое справедливо, если i ui cui
при некотором c>0.
2. Неравенство может выполняться начиная с
некоторого i.
66
67.
• ТЕОРЕМА 13. (предельный признак сравнения)Если
u , u - ряды с положительными
i 1
i
i 1
i
членами, причем
• ui 0,
• существует
ui
limi L 0,
ui
то ряды сходятся или расходятся
одновременно.
67
68.
• ПРИМЕРЫ1
• 1. i
i 1
3 2
• 2.
1
( 1)
i 1 i
68
69.
• ТЕОРЕМА 14. (ПризнакДаламбера)
• 1. Если члены ряда ui положительные и
i 1
начиная с некоторого номера
ui 1
ui 1
q 1
1 ,
ui
ui
то ряд сходится (расходится)
69
70.
2. Если существует пределui 1
limi
L,
ui
то при L<1 ряд сходится,
при L>1 ряд расходится
70
71.
• ТЕОРЕМА 15. (Признак Коши)1. Если начиная с некоторого номера
n
un q 1
n
un 1 ,
то ряд сходится (расходится).
2. Если существует предел lim n n un L,
то при L<1 ряд сходится,
при L>1 ряд расходится
71
72.
• ПРИМЕРЫ1.
k
k!
k 1
2.
k
2
k 1
k
k
72
73.
• ТЕОРЕМА 16. (Интегральный признаксходимости).
• Пусть неотрицательная функция f(x)
является невозрастающей на множестве
[1,+ ).
Ряд f (n) и f ( x)dx
n 1
1
сходятся или расходятся одновременно.
73
74.
• ПРИМЕРЫ1
• 1.
n 1
n
• 2.
1
n 2 n ln n
74
75.
• Для произвольных рядов – критерий Коши(следствие критерия для
последовательностей)
ТЕОРЕМА 17. Для сходимости ряда un
n 1
необходимо и достаточно, чтобы
n p
( 0)( N )( n N )( p) ui
i n
75
76.
• Знакопеременные ряды• ОПРЕДЕЛЕНИЕ 8. Числовой ряд ui
i 1
называется абсолютно
сходящимся, если
сходится ряд ui .
i 1
76
77.
• ТЕОРЕМА 18. Если ряд сходится абсолютно,то ряд сходится.
• ОПРЕДЕЛЕНИЕ 9. Сходящийся ряд
u
i 1
i
сходится условно, если ряд
u
i 1
i
расходится.
77
78.
• Перестановки ряда• ТЕОРЕМА 19. (Коши) Перестановка любого
абсолютно сходящегося ряда – абсолютно
сходящийся ряд, сумма которого равна
сумме исходного ряда.
• ТЕОРЕМА 20. (Риман) Если ряд сходится
условно, то для любого L существует
перестановка ряда, сумма которой равна L.
78
79.
• Знакочередующийся ряд• ТЕОРЕМА 21. (Признак Лейбница) Если ряд
n 1
u1 u2 u3 ... 1 un ...
удовлетворяет условиям
- un 0,
- последовательность u1 , u2 , u3 ,..., un ,...
убывает и является бесконечно малой,
то он сходится
79
80.
• Пример1 1 1
1 ...
2 3 4
• Следствие. Для ряда лейбницевского типа
S2 n S S2 n 1
• Отсюда, для любого k
S S k uk
80
81. ФУНКЦИОНАЛЬНЫЕ ПОСЛЕДОВАТЕЛЬНОСТИ И РЯДЫ
• Функциональная последовательностьf1 ( x), f 2 ( x),..., f n ( x),...
• Функциональный ряд
u ( x)
n 1
n
• Определены на множестве X
81
82.
• ПРИМЕРЫ• 1.
1 nx при 0 x 1/ n
f n ( x)
при 1/ n x 1
0
• 2. Ряд
x x2
xn
1 ... ...
1! 2!
n!
82
83.
• Область сходимости• Предельная функция для
последовательности
• Сумма функционального ряда
• Предельная функция для примера 1.
• ex cумма ряда их примера 2
83
84. Равномерная сходимость
ОПРЕДЕЛЕНИЕ 10. Функциональнаяпоследовательность
f1 ( x), f 2 ( x),..., f n ( x),...
равномерно сходится к функции f(x) на
множестве X, если
0 N n N x X
f n ( x) f ( x)
Для рядов аналогично
84
85.
• Пример 1 – не равномерная сходимость• ТЕОРЕМА 22. (Критерий Коши равномерной
сходимости функц. последовательностей)
• Для равномерной сходимости функц.
последовательности на множестве X
необходимо и достаточно выполнение
следующего условия:
0 N n N p x X
f n ( x ) f n p ( x )
85
86.
• ТЕОРЕМА 23. (Критерий Коши равномернойсходимости функц. рядов)
• Для равномерной сходимости функц. ряда
на множестве X необходимо и достаточно
выполнение следующего условия:
n p
0 N n N p x X ui ( x)
i n
86
87.
• ТЕОРЕМА 24. (Признак Вейерштрасса)Если для функционального ряда
u ( x) x X
n 1
n
существует сходящийся числовой ряд
a
n 1
n
такой, что при всех x un ( x) an , то функц. ряд
сходится равномерно.
МАЖОРАНТА
87
88.
• ПРИМЕРsin 2 x
2
n
n 1
• Признак Вейерштрасса ДОСТАТОЧНЫЙ, НО
НЕ НЕОБХОДИМЫЙ.
n
• ПРИМЕР.
1
, x 1,1
un ( x )
n
88
89.
• ТЕОРЕМА 25. Пусть последовательностьНЕПРЕРЫВНЫХ функций
f1 ( x), f 2 ( x),..., f n ( x),...
сходится равномерно на отрезке [a,b] к
функции f(x).
Тогда функция f(x) также НЕПРЕРЫВНАЯ.
Для рядов аналогично.
Условие ДОСТАТОЧНОЕ, не
НЕОБХОДИМОЕ
89
90.
• ТЕОРЕМА 26. Пусть последовательностьНЕПРЕРЫВНЫХ функций
f1 ( x), f 2 ( x),..., f n ( x),...
сходится РАВНОМЕРНО на отрезке [a,b] к
t
функции f(x).
Тогда последовательность Fn (t ) a f n ( x)dx
сходится равномерно на отрезке [a,b] к
функции
t
F (t ) f ( x)dx.
a
90
91.
• Для всего промежуткаb
b
lim f n ( x)dx lim f n ( x) dx
a
a
• Для рядов
b
un ( x) dx un ( x)dx
a
n 1
n 1 a
b
91
92.
• ТЕОРЕМА 27. Пусть функции fn(x) непрерывнодифференцируемы на отрезке [a,b], причем
- последовательность производных f n(x)
РАВНОМЕРНО сходится (к функции g(x)),
- При некотором c [a,b] последовательность
{fn(c)} сходится.
ТОГДА
- последовательность {fn(x)} сходится
равномерно (к функции G(x)),
- функция G(x) дифференцируемая и G (x)=g(x).
92
93.
• Иная форма записи:lim
f
(
x
)
lim f n ( x).
n
• Для рядов: при соответствующих условиях
un ( x) un ( x)
n 1
n 1
93
94. СТЕПЕННЫЕ РЯДЫ
• ОПРЕДЕЛЕНИЕ 11. Степенным рядомназывается функциональный ряд вида
a0 a1 x x0 ... an x x0 ... an x x0
n
n
n 0
• Далее будем рассматривать случай x0=0.
94
95.
• Область сходимости степенного ряда• Всегда сходится в 0.
n
n
!
x
• Может сходиться только в 0
n 0
• Может сходиться абсолютно при любом x
xn
n 0 n !
95
96.
• ТЕОРЕМА 28. Пусть степенной ряд сходитсяпри некотором x 0 и сходится. не всюду
Существует такое число R>0 (радиус
сходимости), для которого ряд сходится
абсолютно при |x|<R и расходится при
|x|>R .
• Если сходится всюду, то полагают R= .
96
97.
• Основа доказательства:• Если ряд an x0n ( x0 0) сходится, то при
n 0
|x1|<|x0| ряд an x1n сходится абсолютно.
n 0
R=sup{x:
n
|
a
|
x
ряд n
n 0
сходится}
Концы промежутка???
97
98.
• Для нахождения радиуса сходимостиможно использовать признаки Даламбера
и Коши
• ПРИМЕР.
n
x
n 1 n
98
99. СВОЙСТВА СУММЫ СТЕПЕННОГО РЯДА
• ТЕОРЕМА 29. Пусть R>0 радиуссходимости степенного ряда, число
r (0, R). На отрезке [ r, r] степенной ряд
сходится равномерно.
• СЛЕДСТВИЕ. Сумма степенного ряда
непрерывна на интервале ( R, R).
99
100.
• ТЕОРЕМА 30. Пусть R>0 радиуссходимости степенного ряда
a x
n 0
n
n
.
Радиус сходимости степенных рядов
na x
n 1
n
n 1
n 1
x
, an
,
n 1
n 0
100
101.
• полученных почленнымдифференцированием и интегрированием
исходного ряда, также равен R.
101
102. РАЗЛОЖЕНИЕ ФУНКЦИЙ В СТЕПЕННОЙ РЯД
• ОПРЕДЕЛЕНИЕ 12. Говорят, что функция f(x)разлагается в степенной ряд на интервале
( R, R), если существует степенной ряд,
сумма которого на этом интервале равна
f(x).
• Функция, которая разлагается в степенной
ряд, называется аналитической на ( R, R).
102
103. СВОЙСТВА АНАЛИТИЧЕСКИХ ФУНКЦИЙ
1. Аналитическая функция имеетнепрерывные производные любого
порядка.
УСЛОВИЕ НЕОБХОДИМОЕ, НО НЕ
ДОСТАТОЧНОЕ!
2. Если функция аналитическая, то
коэффициенты степенного ряда
определяются однозначно.
103
104.
• Еслиf ( x) an x
n
на ( R, R),
n 0
• то
f ( n ) (0)
an
.
n!
104
105.
• Рядn 0
f
(n)
(0) n
x
n!
называется рядом
Тэйлора (или Маклорена) функции f(x).
105
106.
• Когдаf ( x)
n 0
f
(n)
(0) n
x
n!
на области сходимости ряда?
106
107.
Формула Тейлораn
f ( x)
i 0
f
(i )
(0) i
x Rn ( x)
i!
Необходимое и достаточное условие:
limn Rn ( x) 0
при всех x из интервала сходимости.
107
108.
• Остаточный член в форме Лагранжа:n 1
x
n 1
Rn ( x)
f
( )
n 1 !
x .
108
109.
lim n
x
n
n!
0
для всякого x (можно рассмотреть ряд)
• ТЕОРЕМА 31. Если для каждого x из
интервала существует число M, для
которого
(n)
f
( x) M ,
то функция аналитическая.
109
110.
• По этому признаку при x ( , )2
n
x x
x
e 1 ...
1! 2!
n 0 n !
x
3
5
2
4
2 n 1
x
x
x
n
sin x x ... 1
3! 5!
2n 1 !
n 0
2n
x
x
n x
cos x 1 ... 1
2! 4!
2 n !
n 0
110
111.
• Вычисленияe ,cos
1
sin t
• Интегралы (считаем, что
1 при t=0)
t
x
sin t
0 t dt
111
112.
• Можно доказать: при x ( 1,1)2
3
n
x x
n 1 x
ln(1 x) x ... 1
2 3
n
n 1
1 ... n 1
1
2
n
x ...
x
1 x 1 x
1!
2!
n!
n 0
112
113. ФУНКЦИИ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ
• Рассматриваем функции, определенные наобласти X плоскости или пространства (R2,
R3)
f: X R.
Обозначения: f(M) (M X) или f(x,y), f(x1,x2),
f(x,y,z), f(x1,x2,x3)
113
114.
Окрестности точки M=(x1,x2,x3) X:шары {N X: (N, M)< } или
параллелепипеды {(y1,y2,y3) X:|yi xi|< }
114
115.
• ОПРЕДЕЛЕНИЕ 13. Точка M называетсявнутренней точкой множества X , если она
принадлежит X вместе с НЕКОТОРОЙ
окрестностью.
• Точка M называется внешней точкой
множества X , если НЕКОТОРАЯ ее
окрестность не пересекается с X.
• Точка M называется граничной точкой
множества X, если она не является ни
внутренней, ни внешней.
115
116.
• Иначе. Точка граничная, если в ЛЮБОЙ ееокрестности есть как точки, входящие в X,
так и точки, не входящие в X.
• Граничные точки множества и его
дополнения совпадают.
116
117.
• ОПРЕДЕЛЕНИЕ 14. Множество X называетсяоткрытым, если все его точки внутренние
(не содержит граничных точек).
• Множество X называется замкнутым, если в
него входят все граничные точки.
• ТЕОРЕМА 32. Дополнение открытого
множества замкнутое.
• Дополнение замкнутого множества
открытое.
117
118.
• ОПРЕДЕЛЕНИЕ 15. Множество называетсяограниченным, если оно содержится в
некотором круге (шаре).
• (Непрерывная) кривая - вспомним!
• ОПРЕДЕЛЕНИЕ 16. Множество называется
связным, если любые две его точки можно
соединить кривой.
118
119.
• ОПРЕДЕЛЕНИЕ 17. Последовательностьточек M1, M2,…, Mn,… в Rk называется
сходящейся, если существует точка
A Rk такая, что
0 N n N M n , A .
• A – предел последовательности, Mn A
119
120.
• ТЕОРЕМА 33. Для того, чтобы, A a , a ,..., a
необходимо и достаточно выполнение
M n A M n x , x ,..., x
(n)
1
( n)
2
(n)
k
1
2
k
условий
( n)
1
x
a1 ,..., x
( n)
k
ak .
Предел последовательности если существует, то
единственный.
120
121.
• ОПРЕДЕЛЕНИЕ 18. Последовательностьточек M1, M2,…, Mn,… в в Rk называется
фундаментальной, если
0 N n N p M n , M n p .
121
122.
• ТЕОРЕМА 34. (Критерий Коши)Сходимость последовательности точек
в Rk равносильна ее
фундаментальности.
122
123.
НАПОМИНАНИЕ. Множество X Rk ограниченное,если оно содержится в некотором шаре, т.е.
для некоторого числа A
( M X) ( (O, M)<A)
Равносильно с параллелепипедом
Сходящаяся последовательность ограничена.
123
124.
• ТЕОРЕМА 35. (БольцаноВейерштрасса)Из любой ограниченной
последовательности точек в Rk можно
извлечь сходящуюся
подпоследовательность.
124
125.
• ОПРЕДЕЛЕНИЕ 20.1. Число b - предел функции f(M) в
точке A, если из того, что Mn A
(Mn A) следует, что f(Mn) b.
2. Число b - предел функции f(M) в
точке A, если
0 0 M , A
f (M ) b .
126.
• ОБОЗНАЧЕНИЯlim M A f ( M ) b
lim x1 a1 f ( x1 , x2 ) b
x2 a2
126
127.
• ПРЕДЕЛ НА БЕСКОНЕНОСТИ• ОПРЕДЕЛЕНИЕ 21. Число b - предел
функции f(M) на бесконечности, если
0 a 0 O, M a
f (M ) b .
127
128.
• Арифметические операции• Если b=0, то функция бесконечно
малая в точке M.
• ПРИМЕР.
• (x 1)p+(y 2)q при p,q>0 – бесконечно
малая в точке (1,2).
128
129.
• ОПРЕДЕЛЕНИЕ 22.1. Функция f(M) называется непрерывной в
точке A, если
lim M A f ( M ) f ( A).
• 2. Функция f(M) называется непрерывной в
точке A, если
0 0 A, M
f ( M ) f ( A) .
129
130.
• Функция называется непрерывной намножестве X, если она непрерывна в каждой
точке этого множества.
• Пусть u=f(M). Приращение функции в точке
A:
u=f(M) f(A)
A=(a1, a2), M=(a1+ x1, a2+ x2)
u=f(a1+ x1, a2+ x2) f(a1, a2)
130
131.
• Разностная форма непрерывности:lim M A u lim x1 0 u 0
x2 0
131
132.
• Частные приращения:x1 u 1u u (a1 x1 , a2 , a3 ) u (a1 , a2 , a3 )
x2 u 2u u (a1 , a2 x2 , a3 ) u (a1 , a2 , a3 )
x3 u 3u u (a1 , a2 , a3 x3 ) u (a1 , a2 , a3 )
132
133. СВОЙСТВА НЕПРЕРЫВНЫХ ФУННКЦИЙ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ
ТЕОРЕМА 36.Если функции f(M) и g(M) непрерывны в
точке A, то функции f(M) g(M), f(M) g(M),
f(M)/g(M) непрерывны в точке A
(отношение при g(A) 0).
133
134.
Сложная функция.Дано: f(x1, x2, x3),
g(t1, t2)=(x1(t1, t2), x2(t1, t2), x3(t1, t2))
Определена функция
h(t1, t2)=f(x1(t1, t2), x2(t1, t2), x3(t1, t2))
g:R2 R3, h:R3 R
h=g◦f – композиция, суперпзиция
134
135.
ТЕОРЕМА 37.Если функции
x1(t1, t2), x2(t1, t2), x3(t1, t2) непрерывны в точке
(b1, b2),
функция f(x1, x2, x3) непрерывна в точке
a1= x1 (b1, b2), a2= x2 (b1, b2), a3= x3 (b1, b2),
ТО
функция h(t1, t2) непрерывна в точке
(b1, b2).
135
136.
ТЕОРЕМА 38. (Устойчивость знака)Если функция f(M) непрерывна в точке A и
f(A) 0, то существует окрестность точки A,
в которой функция сохраняет знак.
136
137.
• ТЕОРЕМА 39.(Аналог теоремы опромежуточном значении)
Пусть функция f(M) непрерывна на
СВЯЗНОМ множестве X; A,B X. Для
любого числа a, расположенного между f(A)
и f(B), существует точка C X, для которой
f(C)=a.
137
138.
• ОПРЕДЕЛЕНИЕ 23. Замкнутое иограниченное множество называется
компактным.
138
139.
• ТЕОРЕМА 39. (Теорема Вейерштрасса)Функция, непрерывная на компактном
множестве, ограниченная и достигает
наибольшего и наименьшего значений.
139
140. ЧАСТНЫЕ ПРОИЗВОДНЫЕ
• Пусть точка M(x,y) является внутреннейточкой области определения функции f(x,y)
• Отношения
x f ( x, y ) f ( x x, y ) f ( x, y )
,
x
x
y f ( x, y ) f ( x, y y ) f ( x, y )
y
y
140
141.
• Вспомним производные!• ОПРЕДЕЛЕНИЕ 24. Частной производной
функции f(x,y) в точке M(x,y) по переменной x
называется
x f ( x, y )
lim x 0
x
если предел существует.
Аналогично по y
141
142.
• Обозначения:f f
, , f x , f y
x y
• Примеры
x
f ( x, y) arctg
• 1.
y
• 2.
f ( x, y, z) x
yz 2
142
143.
• ОПРЕДЕЛЕНИЕ 25. Функция f(x,y)называется дифференцируемой в точке
(x,y), если
f(x,y)=f(x+ x,y+ y) f(x,y)=
=A x+B y+ 1 x+ 2 y
A,B НЕ ЗАВИСЯТ от x, y
lim x 0, y 0 1=lim x 0, y 0 2=0
1, 2=0 при x= y=0
143
144.
• Другая форма записи.x
2
y
2
f(x,y)=A x+B y+о( )
ЗАМЕЧАНИЕ. Из дифференцируемости
следует непрерывность.
144
145.
• ТЕОРЕМА 40. Если функция f(x,y)дифференцируема в точке M(x,y), то в этой
точке существуют частные производные,
причем
f
f
A,
B
x
y
• ОБРАТНОЕ НЕВЕРНО!
145
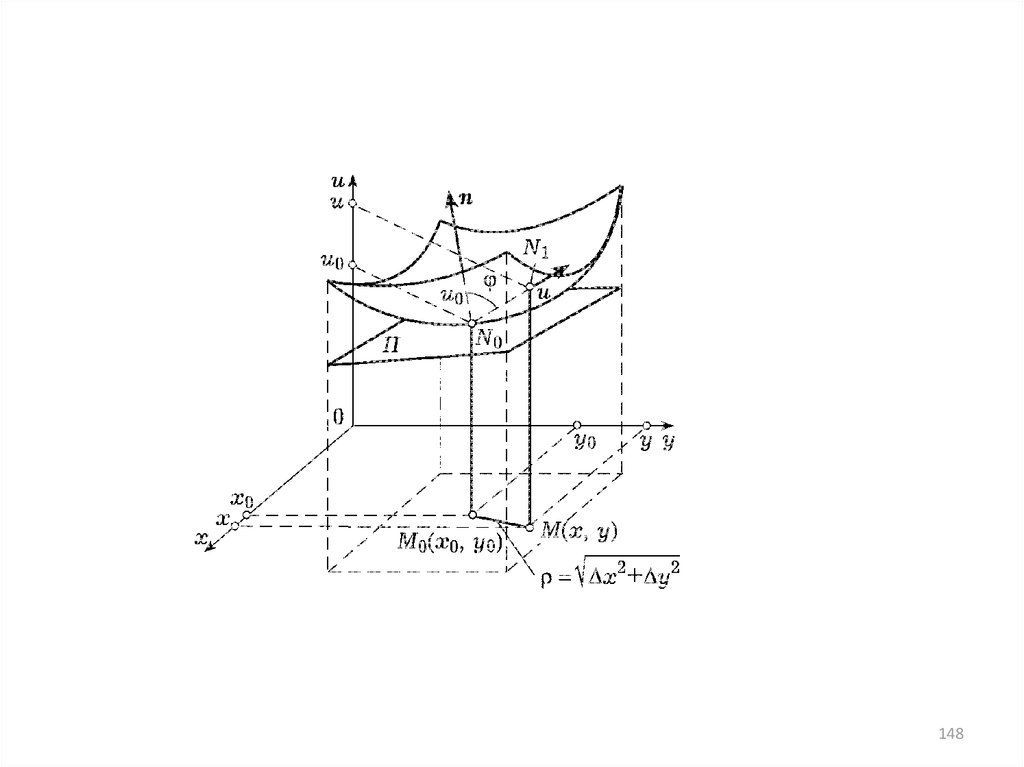
146.
• u(x,y) – график – поверхность.• Что такое «касательная плоскость к
поверхности»?
• На поверхности – точка N0=(x0,y0,u0)
146
147.
• ОПРЕДЕЛЕНИЕ 26. Плоскость , проходящаячерез точку N0, называется касательной
плоскостью к поверхности, если угол
между этой плоскостью и прямой,
проходящей через точку N0 поверхности и
любую точку поверхности N1(x,y,u) N0,
стремится к 0 при N1 N0
147
148.
148149.
• ТЕОРЕМА 41. Если функция u(x,y)дифференцируема в точке (x0,y0), то
касательная плоскость к графику функции в
точке N0 существует и задается уравнением
u
u
u u ( x0 , y0 )
x x0
y y0
x x0 , y0
y x0 , y0
149
150.
• Нормальный вектор к плоскостиu u
n , , 1 A, B, 1
x y
150
151.
• Плоскость проходит через точку N0 .cos
o( )
151
152.
• Достаточное условие дифференцируемости• ТЕОРЕМА 42. Если функция f(x,y) имеет
НЕПРЕРЫВНЫЕ частные производные в
окрестности точки (x,y), то функция в этой
точке дифференцируема.
152
153.
• ОПРЕДЕЛЕНИЕ 27. Дифференциалом(полным) дифференцируемой функции
f(x,y) в точке (x,y) называется
f
f
f
f
df x y dx dy
x
y
x
y
• Частные дифференциалы:
f
f
d x f dx, d y f dy
x
y
153
154. Дифференцирование сложной функции
Дано: f(x1, x2, x3),g(t1, t2)=(x1(t1, t2), x2(t1, t2), x3(t1, t2))
Определена функция
h(t1, t2)=f(x1(t1, t2), x2(t1, t2), x3(t1, t2))
g:R2 R3, f:R3 R
h=g◦f – композиция, суперпозиция
154
155.
• Точка A R2, B=g(A) R3• ТЕОРЕМА 43.
Пусть
- функции xi(t1, t2) (i=1,2,3) дифференцируемы
в точке A,
- функция f дифференцируема в точке B.
ТОГДА
функция h дифференцируема в точке A,
155
156.
• ее частные производные равныx
ht 1 1 t1
h
t
2 x1 t
2
x
2 t
1
x
2 t
2
g x1
x3 t1
g
x2
x
3 t2 g x
3
156
157. ИНВАРИАНТНОСТЬ ФОРМЫ ПЕРВОГО ДИФФЕРЕНЦИАЛА
• h(u,v)=f(x(u,v), y(u,v))• u,v – независимые переменные
h
h
dh du dv
u
v
h
h
dh dx dy
x
y
157
158. ПРАВИЛА ДИФФЕРЕНЦИРОВАНИЯ
d(cu)=cdu
d(u v)=du dv
d(uv)=udv+vdu
d(u/v)=(vdu udv)/v2
158
159. ПРОИЗВОДНАЯ ПО НАПРАВЛЕНИЮ
f(x, y, z)
M0(x0,y0,z0)
Вектор l=(cos , cos , cos ) – единичный
Отложим отрезок длины t
Получим точку
M(x0+tcos ,y0+tcos ,z0+tcos )
g(t) =f(M)
159
160.
• ОПРЕДЕЛЕНИЕ 28. Производной функцииf(x, y, z) в точке M0 по направлению вектора
l называется производная g (t) при t=0, если
она существует.
• Обозначение:
f
l
160
161.
• ТЕОРЕМА 44. Если функция f(x, y, z)дифференцируема в точке M0 , то
производная по любому направлению
существует.
f f
f
f
cos cos cos
l x
y
z
161
162.
• ОПРЕДЕЛЕНИЕ 29. Градиентомдифференцируемой функции f(x, y, z) в точке
M0 называется вектор
f f f
grad f , ,
x
y
z
f
grad f , l
l
Градиент – направление наискорейшего
возрастания функции, скорость – модуль
градиента.
162
163.
• Для двух переменных163
164. ПРОИЗВОДНЫЕ ВЫСШИХ ПОРЯДКОВ
• Производныеf ( x, y )
f ( x, y )
x
2 f ( x, y )
x 2
2 f ( x, y )
x y
f ( x, y )
y
2 f ( x, y )
y x
2 f ( x, y )
y 2
• Пример: f(x, y) =xy
• Определяются индуктивно
164
165.
• ТЕОРЕМА 45. Если смешанные производные2 f 2 f
,
x y y x
непрерывны, то они равны.
СЛЕДСТВИЕ. Смешанные производные не
зависят от порядка дифференцирования, если
они непрерывны.
165
166.
• ОПРЕДЕЛЕНИЕ 30. Функция f(x,y,z)называется n раз дифференцируемой, если
все ее частные производные (n 1)-го
порядка дифференцируемые.
166
167. ДИФФЕРЕНЦИАЛЫ ВЫСШИХ ПОРЯДКОВ
• ОПРЕДЕЛЕНИЕ 31. Дифференциаломвторого порядка функции f(x,y) называется
d2f(x,y)=d(df(x,y)).
167
168.
ff
d 2 f ( x, y ) d dx dy
y
x
f
f 2
f 2
f
d dx d x d dy d y
x
y
x
y
2 f
2 f
2 f
2 f
f 2
f 2
2 dx
dy dx
dx 2 dy dy d x d y
y x
y
x
y
x
x y
2 f 2 2 f
2 f
2 f 2 f 2
f 2
2 dx
dydx
dxdy 2 dy d x d y
x
y x
x y
y
x
y
2 f 2
2 f
2 f 2 f 2
f
2 dx 2
dydx 2 dy d x d 2 y
x
y x
y
x
y
168
169.
x,y НЕЗАВИСИМЫЕ
dx, dy тоже 2
2
2
f
f
f 2
2
2
d
f
dx
2
dydx
dy
Тогда
2
2
x
y x
y
Неинвариантность формы второго
дифференциала
f
d f ( x1 ,..., xn )
dxi dx j
i 1 j 1 xi x j
n
n
2
2
169
170.
• Индуктивно – дифференциалы болеевысоких порядков.
f
d f ( x1 ,..., xn )
dxi dx j dxk
i 1 j 1 k 1 xi x j xk
n
n
3
n
3
• Оператор
d dx dy
x
y
2
d f dx dy f
y
x
2
170
171. ФОРМУЛА ТЕЙЛОРА ДЛЯ ФУНКЦИЙ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ
• Для одной переменной• (n+1) раз дифференцируемая функция F(t)
на интервале, содержащем отрезок [0,1].
n
n 1
F (0) F (0)
F (0) F
(c )
F (1) F (0)
...
1!
2!
n!
n 1 !
171
172.
• Дано:функция f(x,y), (n+1) раз дифференцируемая в
окрестности U точки M0(x0,y0)
точка M(x0+ x,y0+ y) в этой окрестности.
F(t)=f(x0+t x,y0+t y)
То же для функции любого числа переменных.
172
173.
• ТЕОРЕМА 46. Существует точка N U, длякоторой справедливо равенство
f (M ) f (M 0 )
df
M0
1!
d2 f
M0
2!
...
dn f
M0
n!
d n 1 f
N
n 1 !
Все дифференциалы вычисляются при
dx= x, dy= y.
173
174.
• В форме Пеано:f (M ) f (M 0 )
df
M0
1!
d2 f
M0
2!
...
dn f
M0
n!
o( n )
174
175. ЛОКАЛЬНЫЕ ЭКСТРЕМУМЫ ФУНКЦИЙ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ
• ОПРЕДЕЛЕНИЕ 32. Функция f(M) (M Rn)имеет в точке M0 локальный минимум
(максимум), если существует такая
окрестность точки M0 в пределах которой
f(M) f(M0) (f(M) f(M0)).
• Локальные экстремумы это локальные
максимумы и минимумы.
175
176. КВАДРАТИЧНЫЕ ФОРМЫ
• ОПРЕДЕЛЕНИЕ 33. Пусть A – квадратнаясимметрическая матрица n-го порядка.
Функция вида
n
n
F ( x1 ,..., xn ) aij xi x j
i 1 j 1
называется квадратичной формой.
F ( x1,..., xn ) F ( x1,..., xn )
2
176
177.
• ТЕОРЕМА 47. Если функция f(M) (M Rn)имеет в точке M0
-все частные производные
- локальный экстремум,
то
f
xi
0 (i 1,..., n)
M0
ОБРАТНОЕ НЕВЕРНО! Примеры: u=x2+y2+z2,
u=x2+y2 z2
Cтационарные (критические) точки.
177
178. ВИДЫ КВАДРАТИЧНЫХ ФОРМ
• 1. Положительно определенные.F(M)>0 при M=(x1,…, xn) 0
Пример: F(x1, x2)=x12+x22
2. Отрицательно определенные.
F(M)<0 при M=(x1,…, xn) 0
Пример: F(x1, x2)= x12 x22
ЗНАКООПРЕДЕЛЕННЫЕ
178
179.
• 3. ЗнакопеременнаяF(M)>0 при некотором M Rn
F(N)<0 при некотором N Rn
Пример: F(x1, x2)=x12 x22
4. Квазизнакоопределенные
F(M) 0 (F(M) 0) при всех M и F(M)=0 при
некотором M 0
Пример: F(x1, x2)=x12+x22 2x1x2
179
180.
• ТЕОРЕМА 48. Для положительноопределенной квадратичной формы
F(x1,x2,…, xn) существует положительное
число m такое, что
F(x1,x2,…, xn) m(x12 +x22+…+xn2 )
Для отрицательно определенных
F(x1,x2,…, xn) m(x12 +x22+…+xn2 )
180
181.
Функция f (x1,x2,…, xn) триждыдифференцируемая в точке M0.
2 f
i 1 j 1 xi x j
n
d2 f
M0
n
dxi dx j
M0
Квадратичная форма относительно
(dx1,dx2,…,dxn)
181
182.
• ТЕОРЕМА 49. Пусть функция f(M) триждыдифференцируемая в окрестности
стационарной точки M0.
2
d
f
Если форма
M0
- положительно определенная, то в точке M0
локальный минимум.
- отрицательно определенная, то в точке M0
локальный максимум.
- знакопеременная, то в точке M0 локального
экстремума нет.
182
183. КРИТЕРИЙ СИЛЬВЕСТРА
a11a21
a
31
a41
...
a
n1
a12
a13
a14
a22
a32
a42
...
an 2
a23
a33
a43
...
an 3
a24
a34
a44
...
an 4
... a1n
... a2 n
... a3n
... a4 n
... ...
... ann
183
184.
• Угловые миноры• Если 1>0, 2>0,…, n>0, то кв. форма
положительно определенная
• Если 1<0, 2>0, 3<0, 4>0,…, то форма
отрицательно определенная
184
185.
• Случай двух переменных• f(x,y), M0, df=0
2 f
2 f
2 f
A 2 , B
,C 2
x
x y
y
• ТЕОРЕМА 50. Если AC B2>0, то функция
f(x,y) имеет в точке M0 локальный экстремум
(минимум при A>0, максимум при A<0)
Если AC B2<0, то функция f(x,y) не имеет в
точке M0 локального экстремума.
185
186.
Во втором случае:
Форма Ax2+2Bxy+Cy2
A>0
При x=1, y=0 форма положительная
B
B2 2
y C
y
Ax
A
A
2
• При x= B/A, y=1 форма отрицательная
186
187.
• ПРИМЕР• f(x,y)= x2+y2 2x 2y
187
188. НЕЯВНЫЕ ФУНКЦИИ
• Задано уравнение F(x,y,z)=0• Например, x2+y2+z2 1=0
• z(x,y) - ? z 1 x 2 y 2
188
189.
189190.
• Вопросы:• При каких условиях неявная функция
существует? Непрерывная?
Дифференцируемая?
190
191.
• ТЕОРЕМА 51. Пусть- F(x0,y0,z0)=0
-!!!
F
z
0
M0
- F дифференцируема в некоторой
окрестности точки (x0,y0,z0).
ТОГДА
191
192.
• Для любого >0 существуют окрестностьточки (x0,y0)
и непрерывная и дифференцируемая
функция z(x,y), определенная на этой
окрестности, такая, что
- F(x,y,z(x,y))=0,
- |z(x,y) z0|<
192
193.
• Частные производныеF(x,y,z)=0
F
z
x
F
x
z
F
z
y
F
y
z
Пример. xyz=sin(x+y+z)
193
194.
• Для двух переменныхF(x,y)=0
F
0
y
F
dy
x
F
dx
y
Пример. sin(x2+y2)=exy
194
195.
• Касательная плоскость к поверхности,заданной уравнением F(x,y,z)=0 в точке
M0(x0,y0,z0).
• Полагаем grad F(M0) 0
• Уравнение касательной плоскости
F
x
F
x x0
y
M0
F
y y0
z
M0
z z0 0
M0
195
196.
• Градиент – нормальный вектор ккасательной плоскости (к поверхности)
grad F (M ), M M 0
0
0
• Поверхности уровня
• Линии уровня
196
197. УСЛОВНЫЙ ЭКСТРЕМУМ
• Даны:• - функция
• - условие связи.
Требуется найти
• Экстремум в точках, координаты которых
удовлетворяют условию связи
197
198.
• Пример.• z=x2+y2
• Условие связи: x+y=1
198
199.
199200.
• ОПРЕДЕЛЕНИЕ 34. Говорят, что функцияF(x,y,z) достигает в точке M0(x0,y0,z0) условный
максимум (минимум) при условии связи
g(x,y,z)=0, если
- g(x0,y0,z0)=0
- существует окрестность U точки M0 такая, что
для любой точки (x,y,z) U, для которой
g(x,y,z)=0, справедливо неравенство
F(x,y,z) F(x0,y0,z0) (F(x,y,z) F(x0,y0,z0)).
200
201.
• ТЕОРЕМА 52. Если в точке M0(x0,y0,z0)достигается условный экстремум функции
F(x,y,z) при уравнении связи g(x,y,z)=0 и при
этом grad g(M0) 0, то
grad g(M0) | | grad F(M0),
т.е. существует число такое, что
grad F(M0)+ grad g(M0)=0.
201
202.
• (x,y,z, )=F(x,y,z)+ g(x,y,z) – функцияЛагранжа,
• - множитель Лагранжа
• Уравнения Лагранжа – НЕОБХОДИМЫЕ
условия условного экстремума:
0
x y z
202
203.
• ПРИМЕР• z=x2 y2
• x2+y2=1
203
204.
• В многомерном случаеF(x1,x2,…, xn) – целевая функция
• Уравнения связи
gi(x1,x2,…, xn)=0 (i=1,2,…,k), k<n
204
205.
• (x1,x2,…, xn, 1, 2,…, k)=k
=F(x1,x2,…, xn) +
g ( x ,..., x )
i 1
i
i
1
k
– функция Лагранжа
205
206.
• Необходимые условия экстремума –уравнения Лагранжа
0 j 1,..., n
x j
0 i 1,..., k
i
• (n+k) уравнений с (n+k) неизвестными
206
207. Двойной интеграл
Объем криволинейного цилиндра
Функция z=f(x,y)>0
Область D на плоскости
Объем цилиндра (простого) мы знаем
207
208.
Пусть область D прямоугольник [a,b] [c,d]4 этапа
1. Разбиение на малые прямоугольники
2. Выбор точек
3. Нахождение интегральной суммы
4. Переход к пределу
208
209.
• 1.• Выбираем точки a=x0<x1<…<xn=b
xi=xi xi 1 (i=1,…,n)
Выбираем точки c=y0<y1<…<ym=d
yj=yj yj 1 (j=1,…,m)
Разбиение - прямоугольнички Dij со
сторонами xi, yj
Площадь Sij= xi yj
(nm штук)
209
210.
• 2. В каждом прямоугольничке – точкиMij=( ij, ij)
210
211.
• 3. Интегральная суммаf ij , ij Sij
n
m
i 1 j 1
• Приближение к объему…
• Диаметр Dij равен xi 2 y j 2
max
xi 2 y j 2
211
212.
• 4. ОПРЕДЕЛЕНИЕ 35. Двойным интеграломназывается
I lim 0 ,
если он существует.
Обозначения:
f ( x, y )dxdy,
D
f (M )dS
D
Функция называется интегрируемой.
212
213.
• ЗАМЕЧАНИЕ. Интегрируемая функцияограниченная
• Вопросы:
• Когда двойной интеграл существует?
• Если существует, как его вычислять?
1dxdy
D
213
214.
• ТЕОРЕМА 53. Если функция f(x,y)непрерывна в области D, то двойной
интеграл существует.
• Если ограниченная функция непрерывна во
всех точках области D кроме точек,
расположенных на некоторой спрямляемой
кривой (или нескольких спрямляемых
кривых), то функция интегрируема.
214
215.
• ДВОЙНОЙ ИНТЕГРАЛ ПО ПРОИЗВОЛЬНОЙОБЛАСТИ D, ОГРАНИЧЕННОЙ ОДНОЙ ИЛИ
НЕСКОЛЬКИМИ СПРЯМЛЯЕМЫМИ
КРИВЫМИ
• Строим прямоугольник D D
• Определим функцию
( x, y ) D
f ( x, y ) при
F ( x, y )
при ( x, y ) D \ D
0
215
216.
• 1. Разбиение области произвольнымиспрямляемыми кривыми. Получаем
подобласти Di с площадями Si (i=1,…,n)
• 2. Выбираем точки Mi Di
• 3. Интегральная сумма
n
f ( M i ) Si
i 1
216
217.
4. Диаметр области Didiam (Di)=sup{ (x,y):x,y Di}
=max{diam (Di)}
f ( x, y)dxdy lim
0
D
217
218.
• Замечание. Определения двойногоинтеграла в старом и новом смысле
эквивалентны.
218
219. Свойства двойных интегралов
• 1. АддитивностьЕсли функция f(x,y) интегрируема по
области D и область разбита спрямляемой
кривой на две области D1, D2 без общих
внутренних точек, то f(x,y) интегрируема
по обеим областям D1, D2
f ( x, y)dxdy f ( x, y)dxdy f ( x, y)dxdy
D
D1
D2
219
220.
2. Линейностьf g dxdy fdxdy gdxdy
D
D
D
Здесь f,g – функции
, – числа
220
221.
• 3. Произведение интегрируемых функцийявляется интегрируемой функцией.
221
222.
4. Если f и g – функции, интегрируемые в D иf g, то
fdxdy gdxdy
D
D
222
223.
5. Если функция f интегрируема в области D,то функция |f| - также интегрируема в
области D и
f dxdy
D
f dxdy
D
223
224.
6. Если функция f интегрируема в области D,U=sup {f (M ): M D},
V=inf {f (M ): M D},
то существует число [V,U], для которого
fdxdy S D .
D
S(D) – площадь области
224
225.
7. Если функция f непрерывна в связнойобласти D, то существует точка M D, для
которой
fdxdy f (M )S D .
D
225
226. ВЫЧИСЛЕНИЕ ДВОЙНОГО ИНТЕГРАЛА
• На прямоугольнике [a,b] [c,d]d
• Определим функцию I ( x) f ( x, y )dy
c
226
227.
• К доказательству• 1.
• Выбираем точки a=x0<x1<…<xn=b
xi=xi xi 1 (i=1,…,n)
Выбираем точки c=y0<y1<…<ym=d
yj=yj yj 1 (j=1,…,m)
• Разбиение на прямоугольнички
227
228.
• 2. В каждом прямоугольничке – точкиMij=( ij, ij)
• ТЕПЕРЬ
– Выбираем точки i [xi 1, xi], j [yj 1, yj]
– Полагаем ij= i, ij= j
228
229.
• 3.f i , j xi y j
n
m
i 1 j 1
xi f i , j y j
n
m
i 1
j 1
229
230.
• 4. Сначала устремляем к 0max{ yj}
f , y
d
m
j 1
i
j
j
f i , y dy I i
c
n
I x
i 1
i
i
230
231.
• Теперь устремляем к 0max{ xi}
b
n
I x I ( x)dx
i 1
i
i
a
231
232.
• ПРИМЕРЫ1. x 2 y 2 dxdy, D : 0,1 0,1
D
2. e
2 x y
dxdy, D : 1, 1,
D
232
233.
• Вычисление интеграла по произвольнойобласти
• ТЕОРЕМА 55. Пусть функция f(x,y)
интегрируема в области D, ограниченной
прямыми x=a, x=b и графиками функций
y=g(x), y=h(x) (g(x) h(x)).
Если при любом x [a, b] существует
h( x)
I ( x)
g( x )
f ( x, y)dy
233
234.
иb
I ( x)dx
существует, то
a
b
b
h( x)
f ( x, y)dxdy I ( x)dx dx
D
a
a
f ( x, y)dy
g ( x)
Можно интегрировать в другом порядке!
234
235.
• Пример.x R
2
2
y
2
3/2
dxdy, D : x y R
2
2
2
D
235
236.
• Можно разбить на части:• Кольцо
236
237. ЗАМЕНА ПЕРЕМЕННЫХ В ДВОЙНЫХ ИНТЕГРАЛАХ
• Отображение(x(u,v), y(u,v))
- Взаимно однозначно отображает область D
плоскости (u,v) на область D плоскости
(x,y).
- Функции x(u,v), y(u,v) непрерывно
дифференцируемые.
237
238.
• Матрица Якоби:xu xv
y y
v
u
• Якобиан:
xu
D ( x, y )
det
D(u , v)
yu
xv
yv
238
239.
• Полагаем, что якобиан всюду отличен от 0.• Разбиваем область D на прямоугольнички
прямыми u=const, v=const.
• Соответственно область D разбивается на
области, близкие к параллелограммам
239
240.
• Пусть левый нижний угол прямоугольника(u,v), стороны u, v.
Вершины “почти параллелограмма”
A(x(u,v), y(u,v))
B(x(u+ u,v), y (u+ u,v))
C(x(u,v+ v), y (u,v+ v))
240
241.
• Площадь:AB AC abs
x
u
u
abs
x
v
v
x(u u , v) x(u, v)
y (u u, v) y (u, v)
x(u , v v) x(u , v)
y (u, v v) y (u , v)
y
u
D ( x, y )
u
u v abs
y
D
(
u
,
v
)
v
v
• Модуль якобиана – коэффициент искажения
площади, знак связан с ориентацией
241
242.
• Функция f(x,y) интегрируемая на D.• Обозначение:
f (u, v) f ( x(u, v), y(u, v))
• Интегральная сумма
D ( x, y )
f ( M i j ) S ( Di j ) f ( M ij )
ui v j
D(r , )
i
j
i
j
• Диаметры областей связаны неравенствами
a diam( Dij ) diam( Dij ) b diam( Dij )
242
243.
• Переходя к пределу при max{diam Dij} 0,получаем:
f ( x, y)dxdy
D
D
D ( x, y )
f (u, v)
dudv
D(u , v)
243
244.
• Полярные координаты• x=r cos , y=r sin
D( x, y)
r
D( r , )
• ПРИМЕР
1 x y dxdy, D : x y 1, x 0, y 0
2
2
2
2
D
244
245.
• ПРИМЕР (интеграл Эйлера-Пуассона)e
x2
dx
245
246. ПЛОЩАДЬ КРИВОЛИНЕЙНОЙ ПОВЕРХНОСТИ
• На плоскости xy – область D• Поверхность задана уравнением z(x,y)
((x,y) D)
246
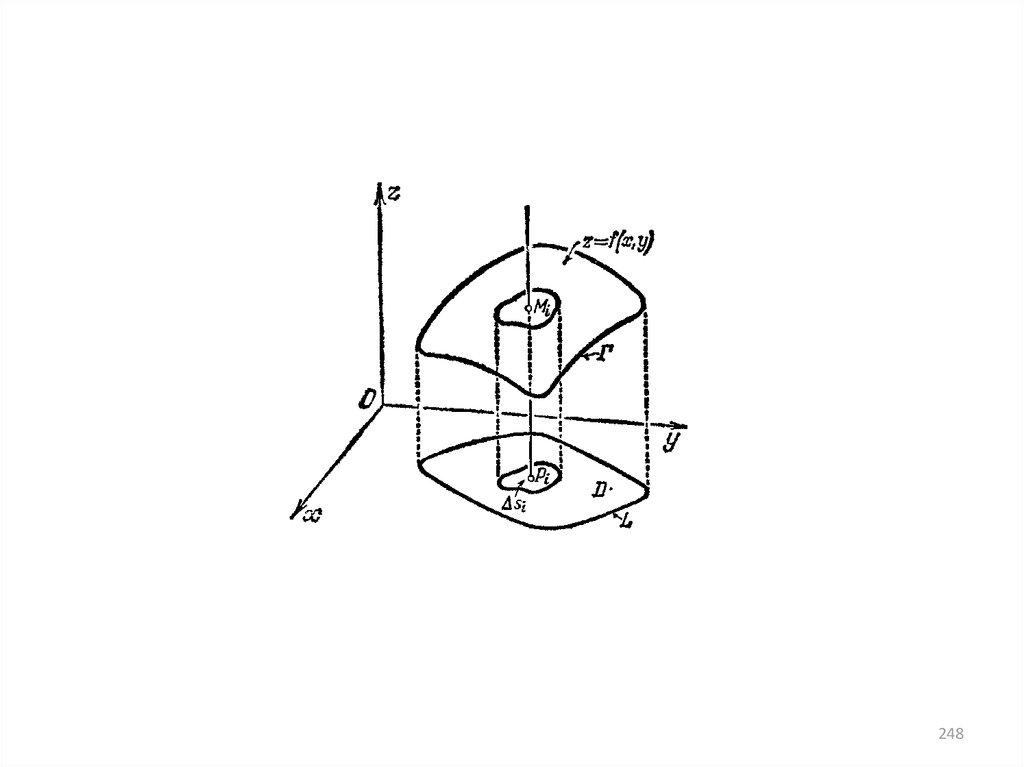
247.
1. Область D разбиваем на части Di сплощадями Si (i=1,…,n)
2. Выбираем точки Pi Di
В каждой точке Mi(Pi ,f (Pi)) проводим
касательную плоскость к поверхности
i – площадь области на касательной
плоскости, проекция которой совпадает с
Di.
247
248.
248249.
249250.
• 3. Находимn
i 1
i
=max{diam (Di )}
• 4. ОПРЕДЕЛЕНИЕ 37. Площадью
поверхности называется
n
( ) lim 0 i
i 1
250
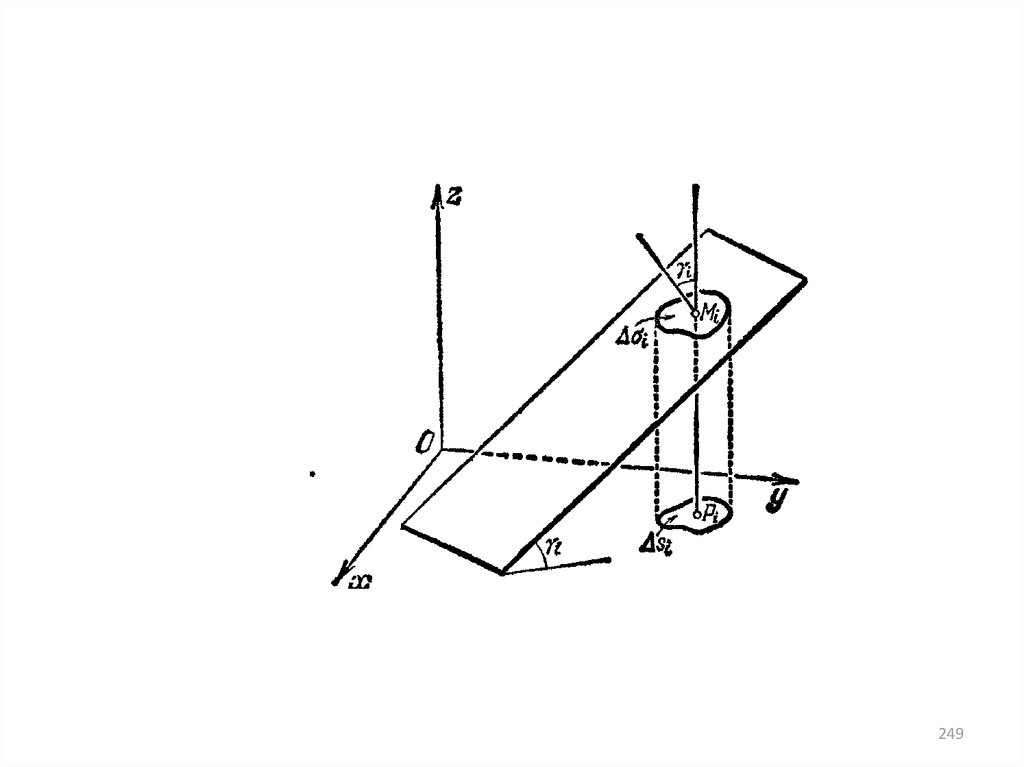
251.
• Вычислениеi – угол между нормалью к поверхности в
точке Mi и осью z
i = Si /|cos i|
z
z
Вектор нормали: , , 1 (в точке Pi)
x y
Вектор k= (0,0,1)
251
252.
2z z
i 1 Si
x y
2
( )
D
2
z z
1 dxdy
x y
2
252
253.
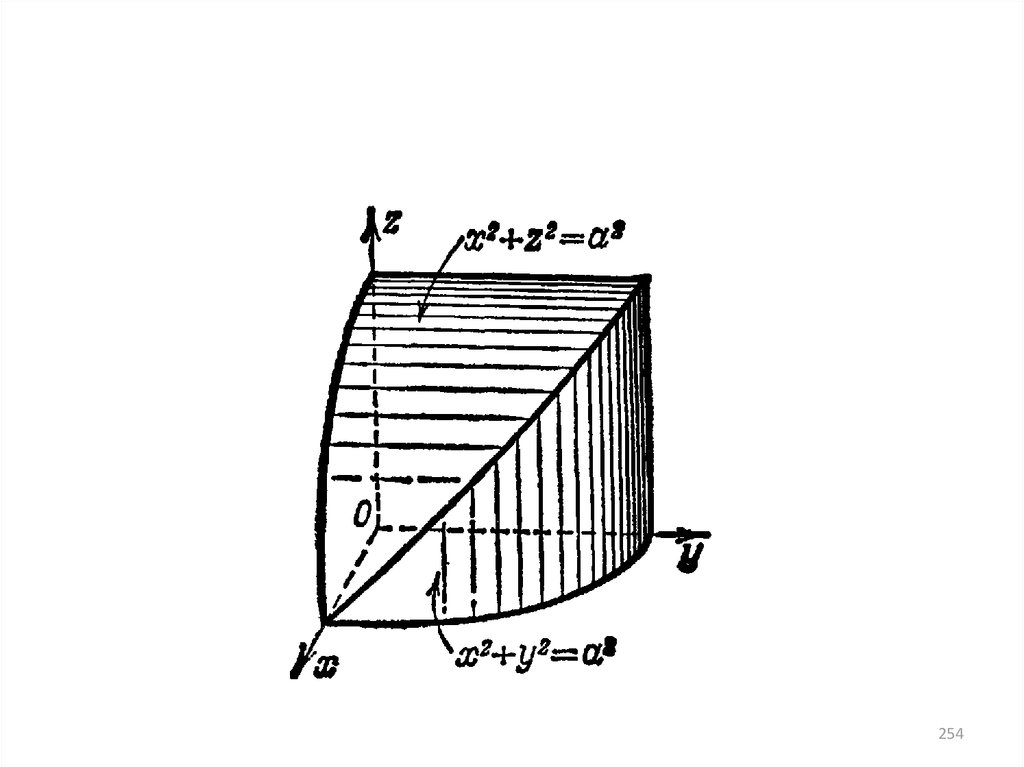
• ПРИМЕРЫ• 1. Площадь сферы x2+y2+z2=R2
• 2. Площадь части цилиндра x2+y2=a2,
которая вырезается цилиндром x2+z2=a2
253
254.
254255. ВЕКТОР-ФУНКЦИЯ СКАЛЯРНОГО АРГУМЕНТА
• Вектор-функция скалярного аргумента tr(t ) x(t ), y(t ), z (t ) x(t )i y(t ) j z (t )k
• Если вектора отложить от начала
координат, то концы векторов пробегают
кривую – годограф вектор-функции.
255
256.
• Предел вектор-функции (совпадает спокоординатным)
• Непрерывность
• Производная r (t ) , если не равна 0,
направлена по касательной к годографу.
256
257.
• Правила дифференцирования• 1. Производная постоянной векторфункции равна 0.
• 2. Производная суммы равна сумме
производных.
• 3. u(t )r(t ) u (t )r(t ) u(t )r (t )
(u(t) – скалярная функция)
257
258.
• 4. (частный случай)kr(t ) kr (t )
• 5. r1 (t ), r2 (t ) r1 (t ), r2 (t ) r1 (t ), r2 (t )
• 6. r1 (t ), r2 (t ) r1 (t ), r2 (t ) r1 (t ), r2 (t )
d
r
d
r
dt
7. Если t=t( ), то
d dt d
направление
касательной не зависит от параметризации
258
259.
• Если r (t ) 0,то плоскость, проходящая через точку
r (t ) и параллельная векторам
годографа
r (t ), r (t )
называется соприкасающейся плоскостью к
кривой.
259
260.
• Особые точки – точки, в которыхr (t ) 0 или не существует
260












































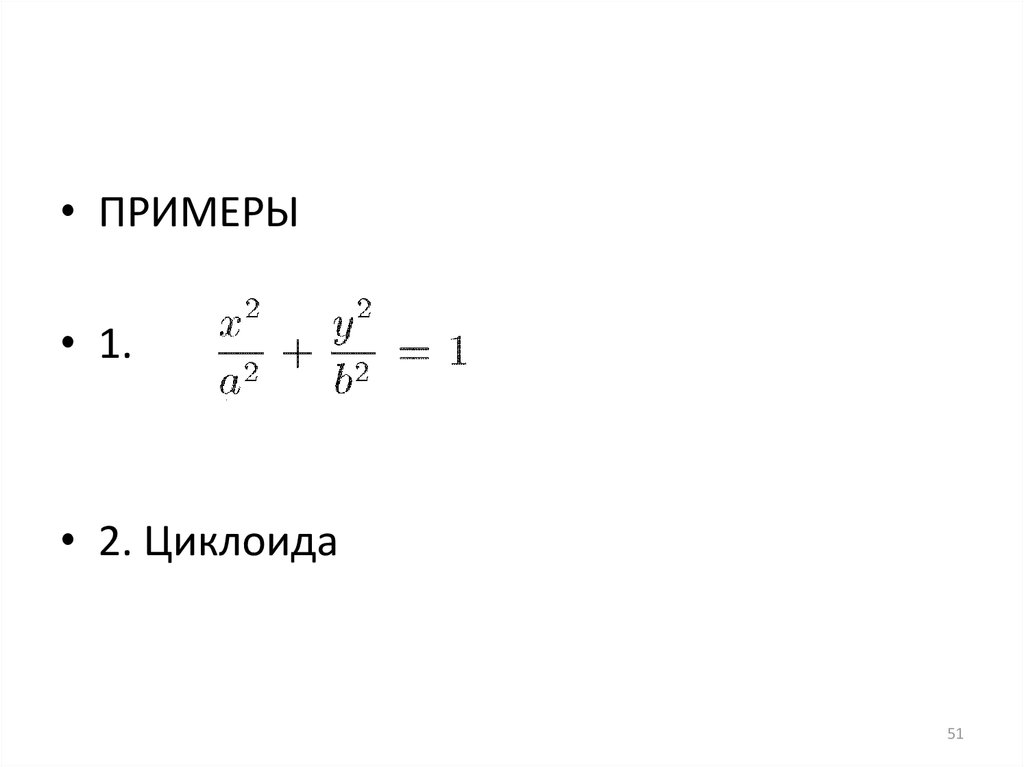





















































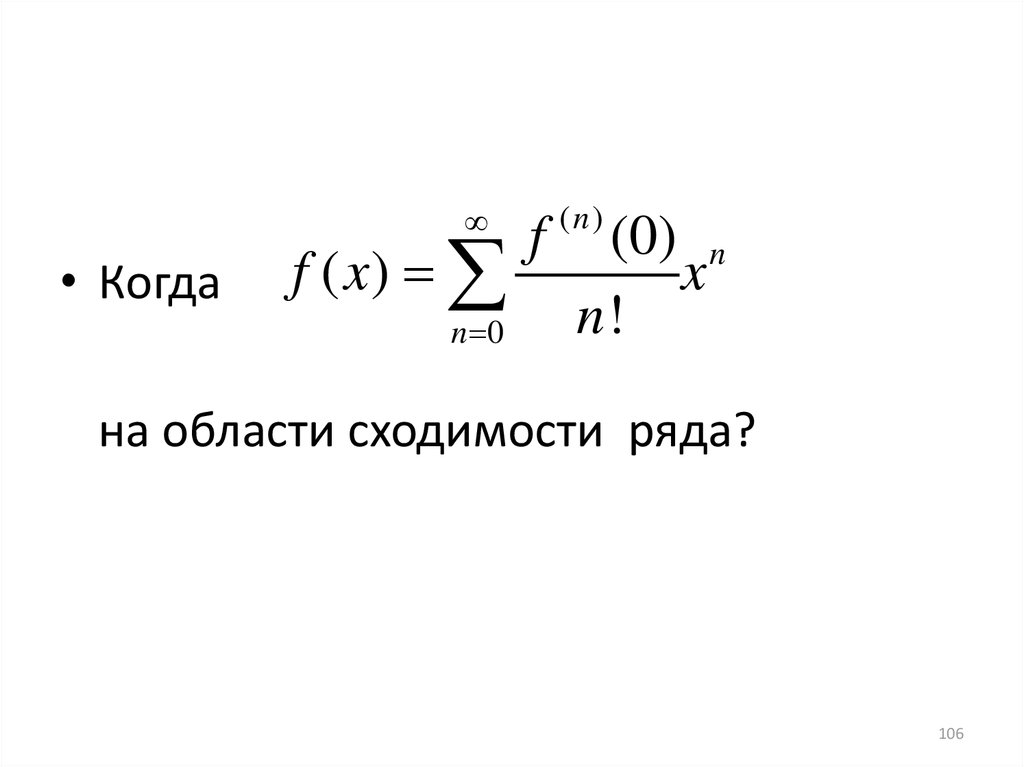



















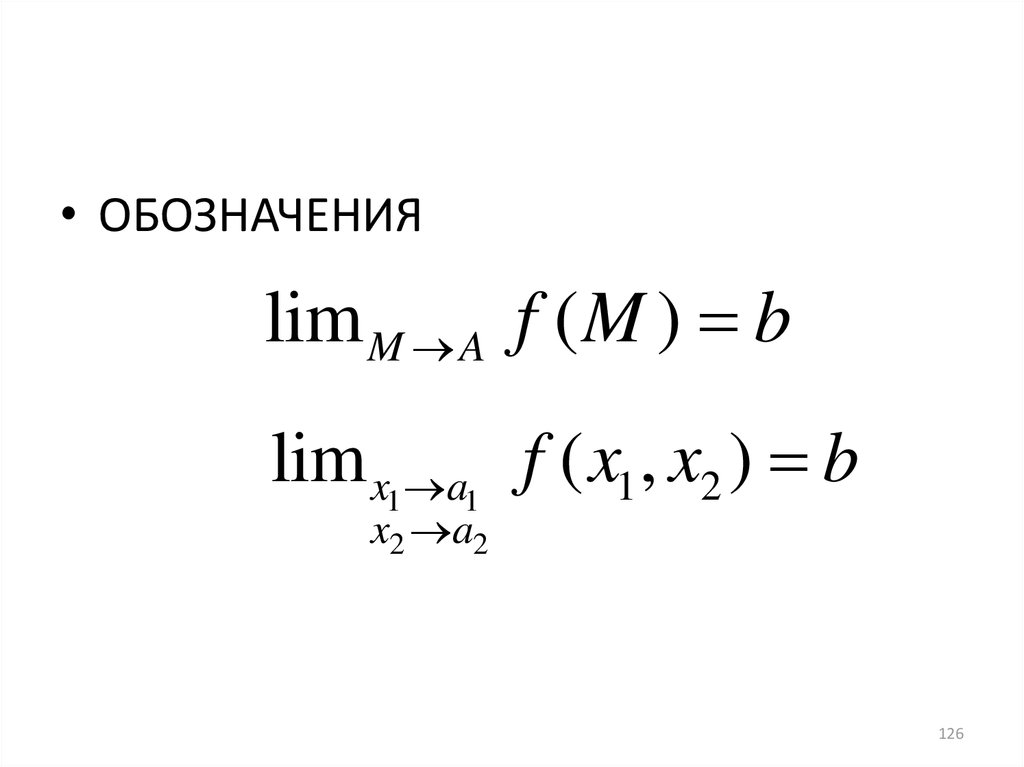

























































































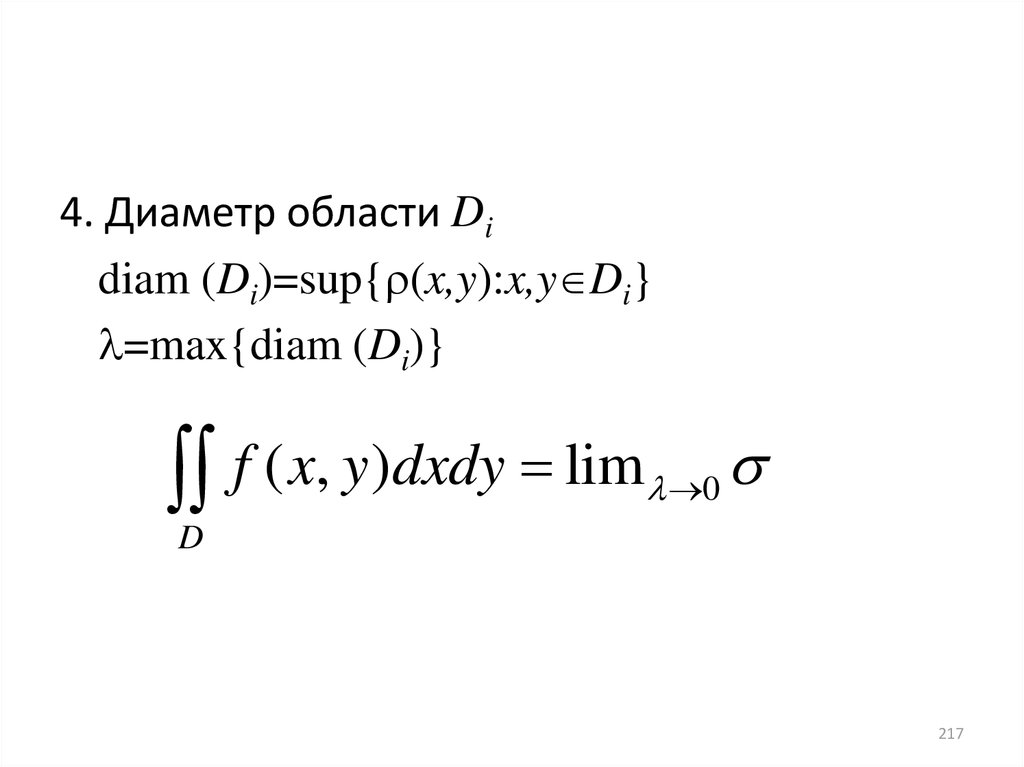














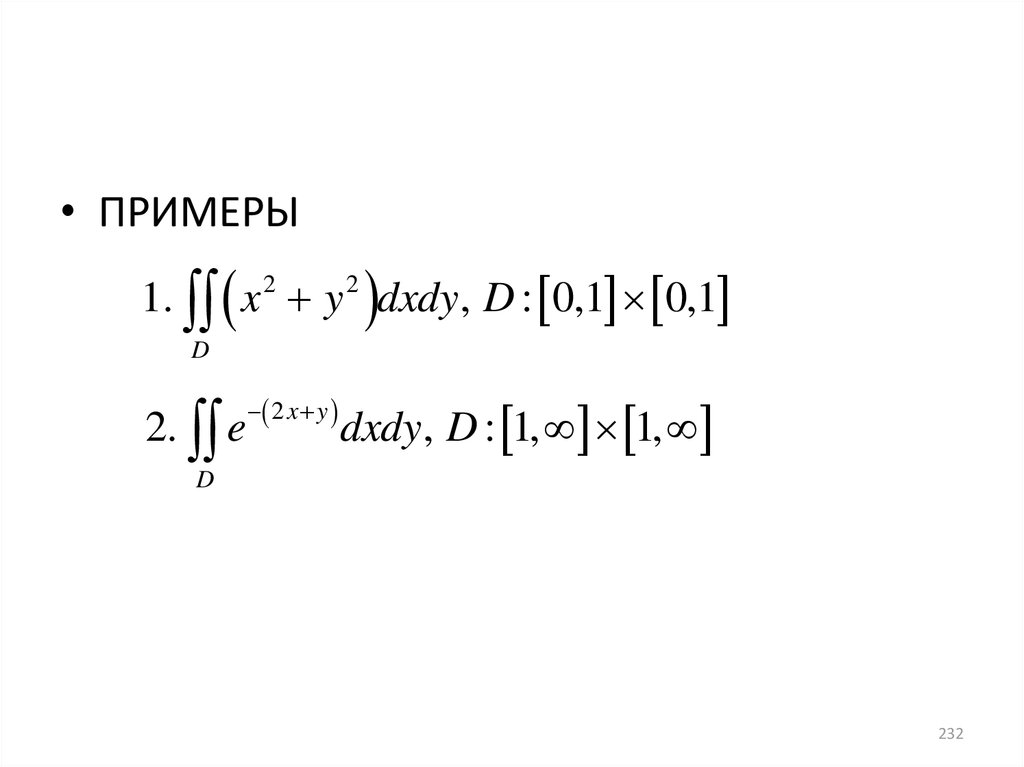

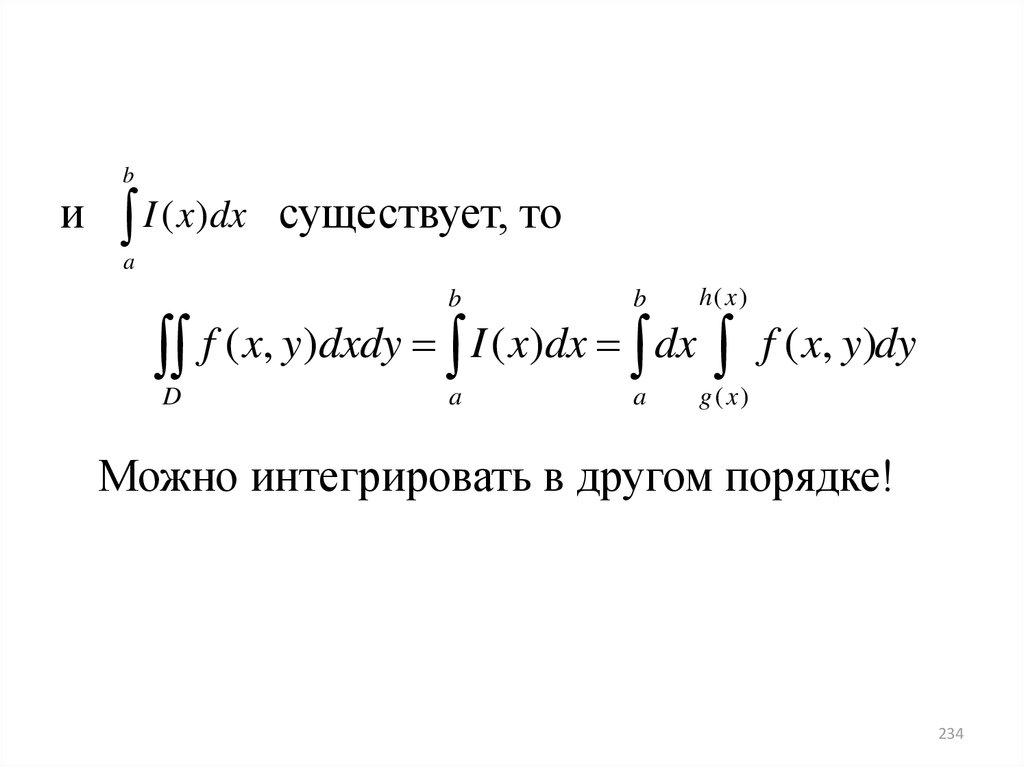























 mathematics
mathematics








