Определенный интеграл. Лекция

1.

Определенный интеграл
Лекция
Попова Елена Александровна
К. пед. н., доцент
доцент кафедры ММиИТ ТЭИ,
СФУ
[email protected]
8 апреля 2020
Красноярск

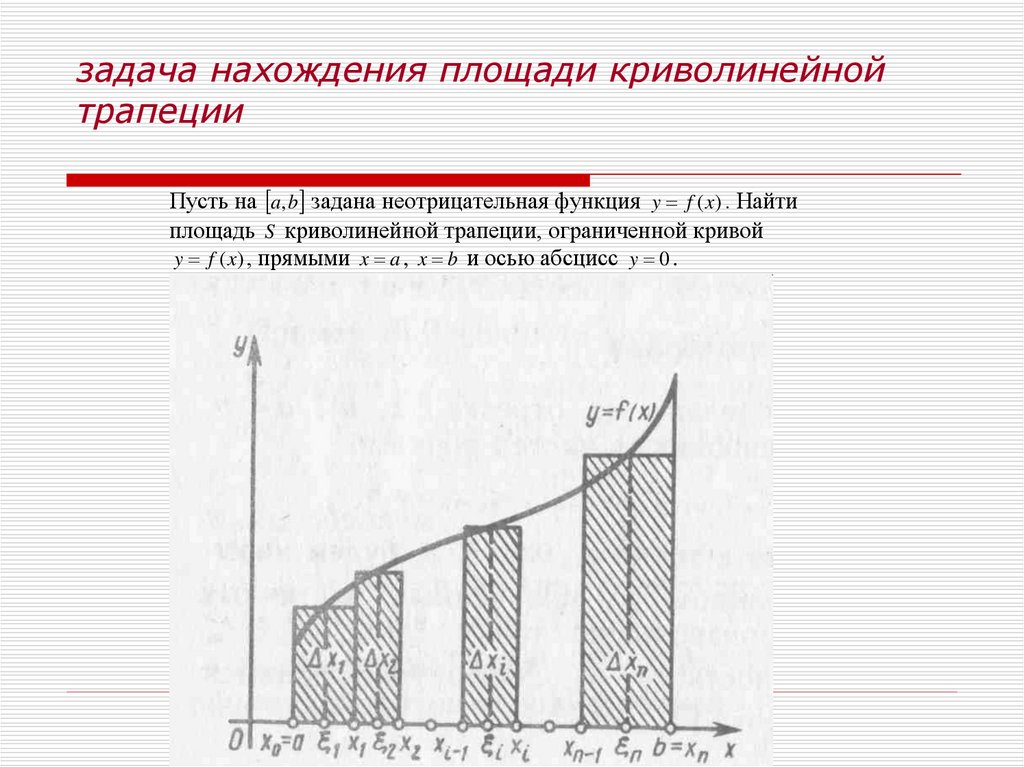
2. задача нахождения площади криволинейной трапеции

Пусть на a, b задана неотрицательная функция y f (x) . Найти
площадь S криволинейной трапеции, ограниченной кривой
y f (x) , прямыми x a , x b и осью абсцисс y 0 .

3.

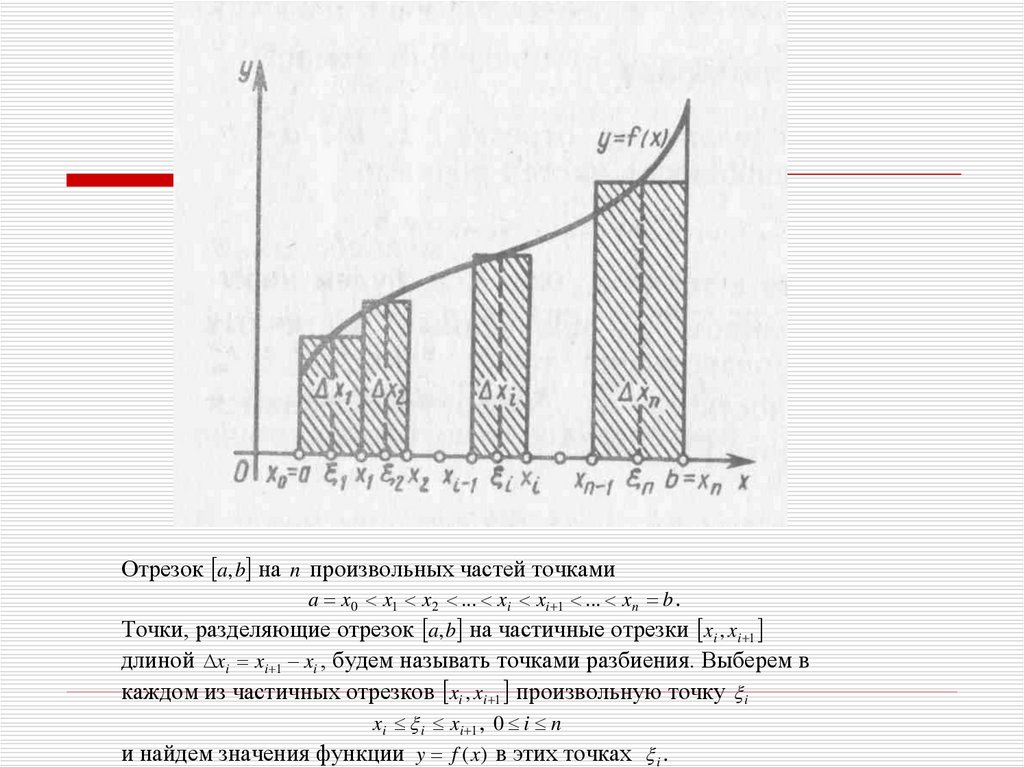
Отрезок a, b на n произвольных частей точками
a x 0 x1 x 2 ... xi xi 1 ... x n b .
Точки, разделяющие отрезок a, b на частичные отрезки xi , xi 1
длиной xi xi 1 xi , будем называть точками разбиения. Выберем в
каждом из частичных отрезков xi , xi 1 произвольную точку i
xi i xi 1 , 0 i n
и найдем значения функции y f (x) в этих точках i .

4.

Рассмотрим сумму произведений
n
S f ( 1 ) x1 f ( 2 ) x2 ... f ( n ) xn f ( i ) xi ,
i 1
которую будем называть интегральной суммой для функции
y f (x) на отрезке a, b . Геометрически эта сумма представляет
собой сумму площадей прямоугольников с основаниями xi и
высотами f ( i ) , т.е. площадь ступенчатой фигуры.

5.

Интегральная сумма зависит как от способа разбиения
отрезка a, b на n частей точками x0 , x1 , x 2 ,..., x n ,
так и от выбора точек i .
Но, если длина максимального частичного отрезка
max xi 0 при n , то, каким бы образом не разбивали
i
отрезок a, b на n частей, и, каким бы образом не выбирали
точки i на этих частичных отрезках, интегральные суммы
образуют последовательность S k , которая сходится
к одному и тому же числу I .
Т.е. определенный интеграл можно интерпретировать как
бесконечную сумму бесконечно малых величин.

6.

Геометрически, если длина максимального частичного
отрезка стремится к нулю, то площадь ступенчатой фигуры
очень незначительно отличается от искомой площади
криволинейной трапеции.

7. 1823 г. определение О. Коши (франц. Математик):

n
Определение. Конечный предел I интегральной суммы f ( i ) xi
i 1
при стремлении max xi к нулю, если он существует, называется
i
определенным интегралом от функции f (x) по отрезку a, b :
n
f ( i ) xi .
max x
I lim
i
i
i 1
Определенный интеграл обозначается символом:
b
I f ( x)dx , где
a
числа a и b называют соответственно нижним и верхним
пределами интегрирования ( a b ), f (x) - подынтегральной
функцией, x - переменной интегрирования.

8.

Теорема 1 (необходимое условие интегрируемости функции).
Интегрируемая на отрезке [a, b] функция f (x) ограничена
на этом отрезке.
Доказательство. Предположим обратное, т.е. что функция f (x) не
ограничена на [a, b] . Тогда при любом разбиении отрезка [a, b] она
неограниченна хотя бы на одном частичном отрезке – пусть это
будет отрезок [ x 0 , x1 ] . Возьмем на остальных частичных отрезках
произвольные точки i i 2,3,..., n и пусть
S1 f ( 2 ) x2 ... f ( n ) xn .
В силу неограниченности f (x) на [ x 0 , x1 ] можно выбрать такую
точку 1 [ x0 , x1 ] , чтобы
f ( 1 )
S1 M
,
x1
где M - произвольное положительное число. Тогда с учетом вида
интегральной суммы S получим:
S f ( 1 ) x1 S1 f ( 1 ) x1 S1 M .
Оказалось, что интегральная сумма S больше любого числа
M 0 , т.е. не имеет конечного предела при max xi 0 , значит, f (x)
i
не интегрируема на отрезке [a, b] . Теорема доказана.

9. Замечание. Обратное утверждение неверно: ограниченная на отрезке функция может быть не интегрируемой на нем.

Теорема 2
(достаточное условие существования определенного интеграла).
Если функция y f (x) непрерывна на отрезке [a, b] , то она
интегрируема на этом отрезке.

10. Основные свойства определенного интеграла

(будем предполагать интегрируемость всех рассматриваемых
функций на выделенных отрезках интегрирования)
1. Интеграл
b
f ( x)dx
был определен для случая a b , обобщим его
a
на другие случаи. Положим
a
f ( x)dx 0
a
как определенный интеграл на отрезке нулевой длины, а также
b
a
a
b
f ( x)dx f ( x)dx , если a b .

11.

2. Аддитивность. Для любых чисел a, b и c справедливо равенство
b
c
b
a
b
c
f ( x)dx f ( x)dx f ( x)dx .
(0)
Доказательство. Положим сначала, что a c b . Пусть точка c
совпадает с одной из точек разбиения с xm , тогда интегральную
сумму S можно разбить на две суммы:
n
m
i 1
i 1
S f ( i ) xi f ( i ) xi
n
f ( i ) xi .
i m 1
Переходя к пределу в этом равенстве при max xi 0 , получим
i
равенство (0).
При другом расположении точек a, b и c доказательство сводится к
первому случаю, нужно только выбрать наибольший отрезок
интегрирования, разбить интегральную сумму на две суммы,
перейти к пределу при max xi 0 и переставить пределы
i
интегрирования (свойство 1). Геометрически: площадь всей
криволинейной трапеции равна сумме площадей двух ее частей.

12.

3. Постоянный множитель можно выносить за знак определенного
интеграла:
b
b
a
a
kf ( x)dx k f ( x)dx ,
k const .
Доказательство. Согласно определению определенного интеграла:
b
n
n
b
kf ( i ) xi k lim f ( i ) xi k f ( x)dx .
kf ( x)dx maxlim
x 0
max x 0
i 1
i 1
a
i
i
i
i
a

13.

4. Определенный интеграл от алгебраической суммы функций
равен алгебраической сумме их определенных интегралов:
b
b
b
a
a
a
[ f ( x) g ( x)]dx f ( x)dx g ( x)dx .
Доказывается исходя из определения определенного интеграла.
Свойство справедливо для любого конечного числа слагаемых.

14.

5. Если имеет место неравенство f ( x) g ( x)
b
b
a
a
f ( x)dx g ( x)dx
для любого x a, b , то
, где a b .
Доказательство. Поскольку f ( x) g ( x) , то при любом дроблении
отрезка a, b на n частей и при любом выборе точек i будет
справедливо и неравенство f ( i ) xi g ( i ) xi .Суммируя и
переходя к пределам соответствующих интегральных сумм
получим
b
b
f ( x)dx g ( x)dx
a
a
.

15.

6. Если функция f (x) интегрируема на отрезке a, b , то справедливо
неравенство:
b
b
f ( x)dx
a
a
f ( x) dx .

16.

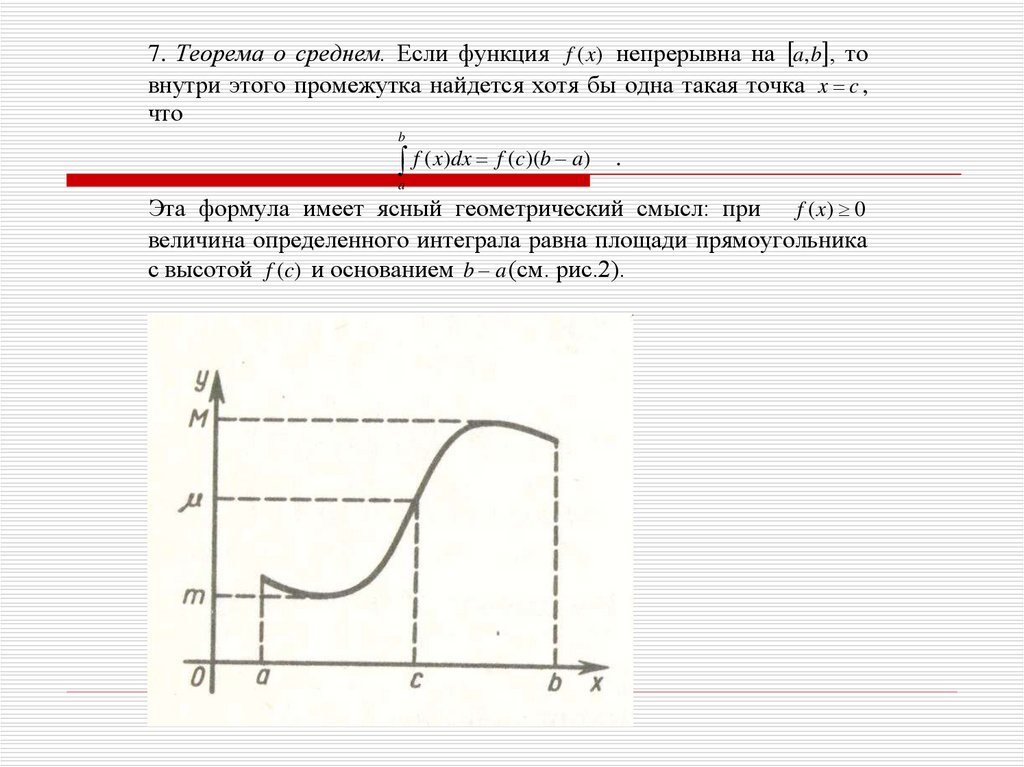
7. Теорема о среднем. Если функция f (x) непрерывна на a, b , то
внутри этого промежутка найдется хотя бы одна такая точка x c ,
что
b
f ( x)dx f (c)(b a)
.
a
Эта формула имеет ясный геометрический смысл: при f ( x) 0
величина определенного интеграла равна площади прямоугольника
с высотой f (c) и основанием b a (см. рис.2).

17. Интеграл с переменным верхним пределом

Если функция f (x) интегрируема на отрезке a, b , то она
интегрируема и на отрезке a, x , где x a, b . Рассмотрим функцию
аргумента x
x
F ( x) f (t )dt .
a
Назовем эту функцию F (x) интегралом с переменным верхним
пределом. Переменная интегрирования обозначена буквой t , чтобы
избежать путаницы с верхним пределом x .

18.

Теорема 3. Непрерывная на отрезке a, b функция f (x) имеет на
этом отрезке первообразную. Одной из первообразных является
функция
x
F ( x) f (t )dt .
a
Доказательство. Чтобы доказать теорему, нужно вывести формулу
/
x
/
F ( x) f (t )dt f ( x) .
a
Возьмем любое значение x a, b и значение x x a, b , x 0 ,
тогда приращение функции F (x) в точке x , с учетом свойства 4
определенного интеграла,
F ( x x) F ( x)
x x
x
x
x x
x
x x
a
a
a
x
a
x
f (t )dt f (t )dt f (t )dt f (t )dt f (t )dt f (t )dt

19.

Отсюда по теореме о среднем (7 свойство определенного
интеграла), получаем:
F ( x x) F ( x)
f (c),
x
где c [ x, x x] . При x 0 , точка c x , и т.к. функция f (x)
непрерывна в точке x , то f (c) f ( x) . Следовательно, переходя в
последнем равенстве к пределу при x 0 , имеем:
F ( x x) F ( x)
lim f (c) lim f (c) f ( x),
x 0
x 0
c x
x
lim
или F / ( x) f ( x) . Что и требовалось доказать.

20.

Итак, установлено, что любая непрерывная на отрезке [a, b]
функция f (x) имеет первообразную в форме определенного
интеграла F (x) с переменным верхним пределом. Поскольку всякая
другая первообразная отличается от F (x) на постоянную величину,
то связь между неопределенным и определенным интегралами
имеет вид:
x
f ( x)dx f (t )dt C , где C const .
a

21.

Замечание. Интеграл с переменным верхним
используется для определения неэлементарных
например:
x
x
пределом
функций,
x
sin t
t dt ,…, которые являются первообразными
0
0
0
sin t
t 2
функций e , cost 2 ,
,…не имеющими первообразных в классе
t
t
e dt ,
2
2
cos t dt ,
элементарных функций, т.е. неопределенные интегралы от этих
функций являются неберущимися.

22. Формула Ньютона-Лейбница

Согласно теореме 3, непрерывная на отрезке [a, b] функция f (x)
имеет первообразную, которая определяется формулой
x
F ( x) f (t )dt +С, где С const .
a
Подставляя x a , учитывая свойство 1 определенного интеграла,
получим
a
f (t )dt F (a) C , 0 F (a) C , откуда C F (a) .
a
Тогда
x
f (t )dt F ( x) F (a) .
a
Полагая x b , получим формулу
b
f ( x)dx F (b) F (a)
a
- формула Ньютона-Лейбница (основная формула интегрального
исчисления).

23. Основные правила интегрирования

I.
b
a
Замена переменной.
f x dx a f t / dt
b
1
2 xdx
Проимер1. Вычислить: 0
.
2
1 x
Решение:
1 x2 t
2 xdx dt
2 xdx
0 1 x 2 при x 0 t 1 2 dt
1 t
при x 1 t 2
2 dt
1
t
1
2
ln t ln 2 ln 1 ln 2
1

24.

Интегрирование по частям
b
a udv uv
b
a
b
a vdu