Similar presentations:
Интегральное исчисление. Определенный интеграл
1. Интегральное исчисление
Определенный интеграл2. Определенный интеграл.
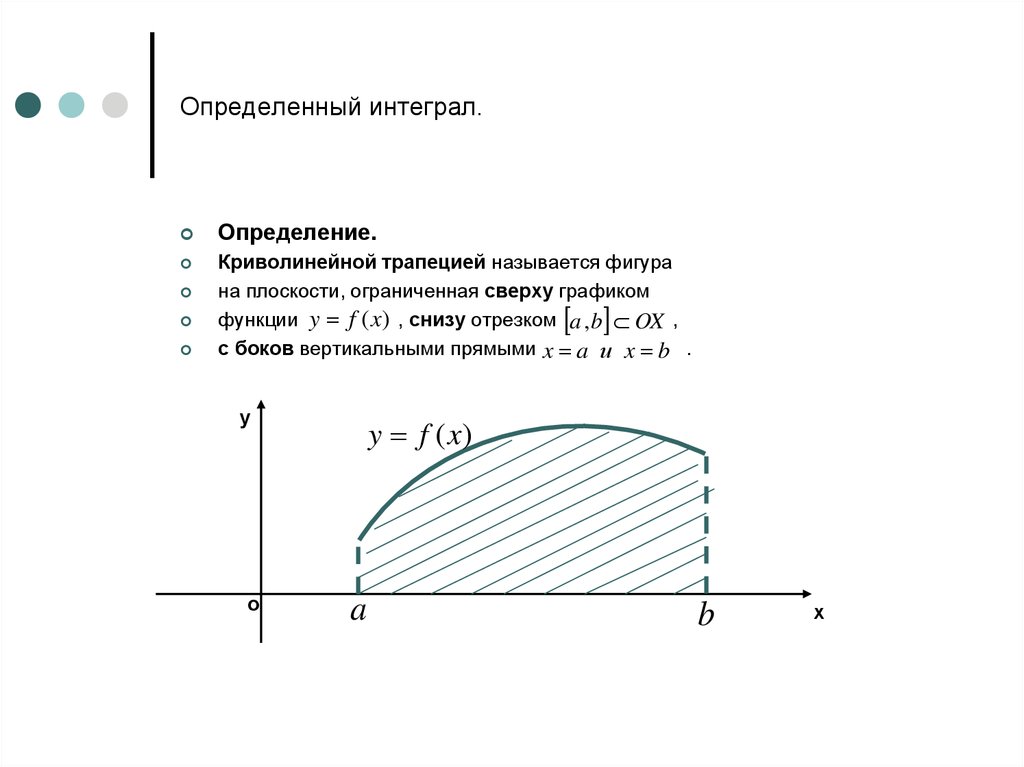
Определение.Криволинейной трапецией называется фигура
на плоскости, ограниченная сверху графиком
функции y f (x) , снизу отрезком a , b OX ,
с боков вертикальными прямыми x a и x b .
y
o
y f (x)
a
b
x
3. Определенный интеграл
Частные случаи криволинейной трапеции.у
у
y f (x)
y f (x)
0
b
a
0
х
у
y f (x)
0
a
b
х
a
b
х
4. Определенный интеграл.
Задача о площадикриволинейной трапеции.
y
o
f ( Pi )
y f (x)
x0 a
x1 x 2 x3
xi xi 1
xn b
x
Si S f ( Pi ) xi
S f ( P ) x
n
S
xi Pi xi 1
n
i
i 1
i
i 1
i
5. Определенный интеграл.
Определение.f (P ) x
n
Выражение
i
i
i 1
называется интегральной суммой.
Рассматриваем всевозможные разбиения
криволинейной трапеции на части такие,
что max( x ) 0
i
Составляем интегральные суммы
и переходим к пределу при 0
f (P ) x
n
Sтрапеции lim
0
i
i 1
i
6. Определенный интеграл.
Определение.Определенным интегралом
от функции
по отрезку
f (x)
называется предел интегральных сумм
n
f (P ) x
i
i
i 1
когда наибольший из участков разбиения
стремится к нулю:
b
a
a, b
max( xi )
f (P ) x
n
f ( x) d x lim
0
i
i
i 1
Геометрический смысл.
f ( x) 0 на a , b
b
a
f ( x)dx S трапеции
7. Определенный интеграл.
Когда существует предел?Когда предел не зависит от способа разбиений?
Теорема..
Если f (x ) непрерывна на
то она интегрируема
[ a, b] ,
(то есть существует предел интегральных сумм
и он не зависит от способа разбиений )
8. Определенный интеграл.
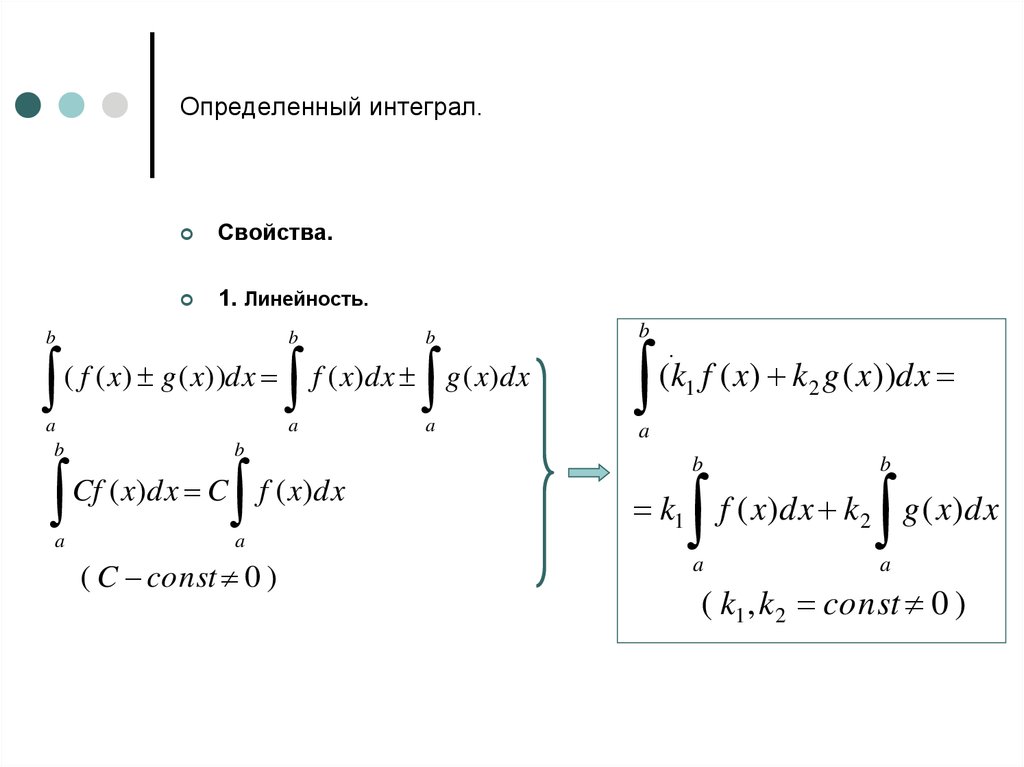
Свойства.1. Линейность.
b
b
( f ( x) g ( x))dx
a
b
a
b
f ( x)dx g ( x)dx
a
a
b
.
(k1 f ( x) k 2 g ( x))dx
a
b
Cf ( x)dx C
b
f ( x)dx
a
( C const 0 )
k1
a
b
f ( x)dx k 2 g ( x)dx
a
( k1 , k 2 const 0 )
9. Определенный интеграл.
Доказательство свойства (для суммы).1. Возьмем разбиение
P1 , P2 ,..., Pn
2. Составим интегральную сумму: ( f ( Pi ) g ( Pi )) xi
n
i 1
n
3.
n
n
( f ( P ) g ( P )) x f ( P ) x g ( P ) x
i 1
x0 a x1 ... xn b
на n частей:
и выберем в каждой части точку:
[ a, b]
i
i
i
i
i 1
i
i 1
i
i
[ a, b]
4. Рассматриваем всевозможные разбиения
на части такие,
что все xi уменьшаются , составляем интегральные суммы
и переходим к пределу при max( xi ) 0
n
n
lim
0
( f ( P ) g ( P )) x
i 1
то есть
i
i
i
lim
0
n
f ( P ) x lim
g ( P ) x
i 1
i
i
b
b
b
a
a
a
0
( f ( x) g ( x))dx f ( x)dx g ( x)dx
i 1
i
i
10. Определенный интеграл.
2. Перестановка пределов интегрирования.b
a
a
3. Аддитивность.
Пусть
тогда
f ( x)dx f ( x)dx
b
a , b a , c c, b
b
c
b
a
a
c
f ( x)dx f ( x)dx f ( x)dx
11. Определенный интеграл.
4. О знаке интеграла.a) f ( x) 0 на a , b
b
f ( x)dx 0
a
b) f ( x) 0 на a , b
b
a
c) f ( x) g ( x) на a , b
f ( x)dx 0
b
a
b
f ( x)dx
g ( x)dx
a
Доказать свойства
самостоятельно
12. Определенный интеграл.
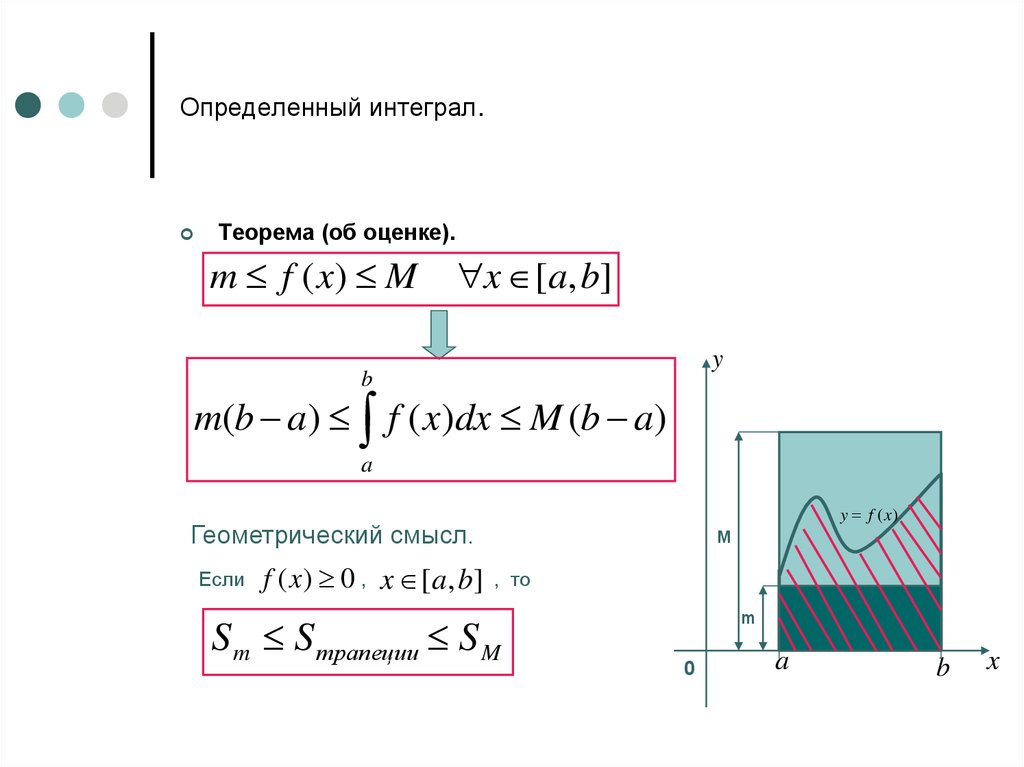
Теорема (об оценке).m f ( x) M
x [a, b]
y
b
m(b a) f ( x)dx M (b a)
a
y f (x)
Геометрический смысл.
Если
f ( x ) 0 , x [ a, b]
M
, то
S m S трапеции S M
m
0
a
b
x
13. Определенный интеграл.
Доказательство.1.
f ( x) m 0 x [a, b]
b
( f ( x) m)dx 0
a
b
b
a
a
f ( x)dx m dx 0
b
f ( x)dx m(b a)
a
b
2. Аналогично:
M f ( x) 0 M (b a) f ( x)dx
a
14. Определенный интеграл.
Определение.Средним значением функции
f (x) на [ a, b]
b
f ср.
называется число
Теорема (о среднем).
f ( x)dx
a
b a
f ( x) непрерывна на [a, b]
P0 [a, b] : f ( P0 ) f ср.
b
a
f ( x)dx f ( P0 )(b a )
15. Определенный интеграл.
Геометрический смысл.b
f ( x)dx f ( P )(b a)
0
a
у
y f (x)
f ( P0 )
0
Если
a
P0
f ( x ) 0 , x [ a, b]
b
, то
х
S трапеции S P0
16. Определенный интеграл.
Доказательство.1. Из непрерывности
m f ( x) M
f (x)
где
x [a, b]
m min f ( x) , M max f ( x)
[ a ,b ]
[ a ,b ]
b
2. Из теоремы об оценке
m(b a) f ( x)dx M (b a)
a
b
1
m
f ( x)dx M
b a a
m f ср. M
3. Из непрерывности
f (x)
P0 [a, b] : f ( P0 ) f ср.
17. Определенный интеграл.
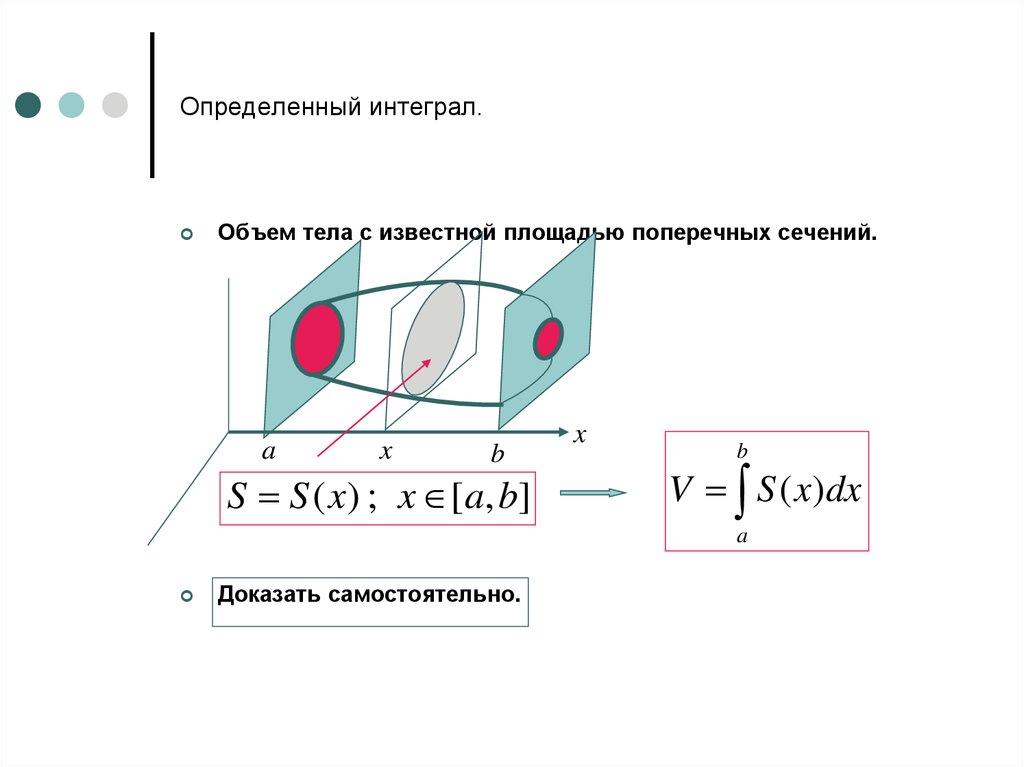
Объем тела с известной площадью поперечных сечений.a
x
b
S S ( x ) ; x [ a, b]
x
b
V S ( x)dx
a
Доказать самостоятельно.
18. Определенный интеграл.
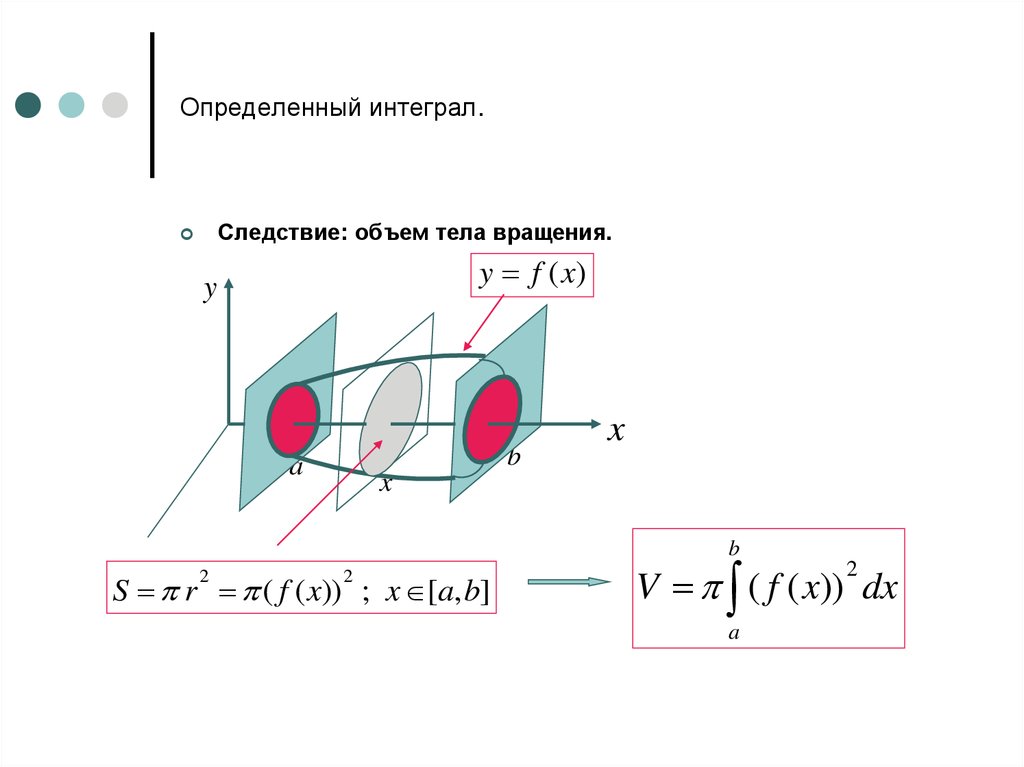
Следствие: объем тела вращения.y f (x)
y
b
a
x
x
b
S r ( f ( x)) ; x [a, b]
2
2
V ( f ( x)) dx
2
a
19. Интеграл с переменным верхним пределом интегрирования.
tf ( x)dx (t ) , где
Рассмотрим
a
( t – переменная).
t [ a , b]
Теорема (Барроу).
Если f (x ) - непрерывная на
[ a, b]
t
то
(t ) f ( x)dx
- дифференцируемая
a
a
t
и
f ( x)dx f (t )
20. Интеграл с переменным верхним пределом интегрирования
Следствие.t
(t ) f ( x)dx
- первообразная для
f (t )
a
Доказательство теоремы Барроу.
1. Возьмем t , t1 [a, b] : t1 t t
t1
(t1 ) (t ) f ( x)dx
t
t
1 1
f ( x)dx f ( P0 ) где P0 [t , t1 ]
t t t
4. t 0 P t
(t ) lim
f (t )
0
t 0 t
2. Тогда
21. Связь определенного и неопределенного интегралов
Формула Ньютона - Лейбница.f (x)
Пусть
- непрерывная на
F (x) - первообразная для f (x)
a , b ;
Тогда
b
f ( x) dx F (b) F (a)
a
b
a
b
f ( x) dx F ( x) a
F ( x) a F (b) F (a)
b
22. Первое доказательство.
1. Возьмем разбиение2.
[ a, b] :
a x0 , x1 , x2 ,..., xn b ; xi xi xi 1.
F (b) F (a)
( F ( xn ) F ( xn 1 )) ( F ( xn 1 ) F ( xn 2 )) ... ( F ( x1 ) F ( x0 ))
n
( F ( xi ) F ( xi 1 ))
i 1
3. По теореме Лагранжа
F ( xi ) F ( xi 1 ) F ( Pi ) xi f ( Pi ) xi
n
F (b) F (a) f ( Pi ) xi
i 1
4. Рассматриваем всевозможные разбиения [ a , b ] на части такие, что все
уменьшаются, составляем интегральные суммы и переходим к пределу при
lim ( F (b) F (a)) lim
0
0
n
f ( P ) x
i 1
i
i
b
xi
max( xi ) 0
F (b) F (a) f ( x)dx
a
23. Второе доказательство.
ПустьТогда
F (x)
- какая-либо первообразная для
x
( x) f (t )dt
f (x) .
- также первообразная для
f (x)
a
( x) F ( x) C
При х=a
a
(a ) f (t )dt 0
a
0 F (a ) C
b
При х=b
C F (a)
(b) f (t )dt F (b) F (a)
a
24. Формула Ньютона-Лейбница.
Примеры.4 2
2
x
1.
1 x dx 4
3
1
4
4
2 1
3
3
4 4
4
2. Интегрирование по частям в определенном интеграле.
b
b
b
udv uv vdu
a
a
Пример:
1
1
a
xe dx xde
x
0
0
x
xe
x1
0
1
e dx e e
x
0
x1
0
e e 1 1



















 mathematics
mathematics








