Similar presentations:
Системы двух линейных уравнений с двумя переменными, как математические модели реальных ситуаций
1. Урок алгебры в 7-м классе " Системы двух линейных уравнений с двумя переменными, как математические модели реальных ситуаций"
2. Когда человек не знает, к какой пристани он держит путь, для него ни один ветер не будет попутным!!! Сенека
3.
4. Тема урока:
Системы двух линейныхуравнений с двумя
переменными, как
математические модели
реальных ситуаций.
5. Цели урока:
www.themegallery.com1
Повторить способы решения систем
2
Отработать навыки решения систем
3
Разработать алгоритм решения задач
4
Научиться составлять систему по
условию задачи
6. Рассмотрим систему двух линейных уравнений с двумя переменными
• Что называют решением системы?•• Является
Что значит
систему
лирешить
пара чисел
(5;2) уравнений?
системы?
• решением
Сколько может
иметь решений система
• линейных
Пара чиселуравнений?
(-3;-2)?
7.
Как решить систему линейных уравненийс двумя неизвестными?
8. Способы решения систем линейных уравнений с двумя неизвестными.
Графический способСпособ подстановки
Способ алгебраического
сложения
www.themegallery.com
(x;y)
9.
ух
10. Дана система уравнений
При каких к и в система имеет:• Единственное решение?
• Не имеет решений?
• Имеет бесконечно много решений?
11.
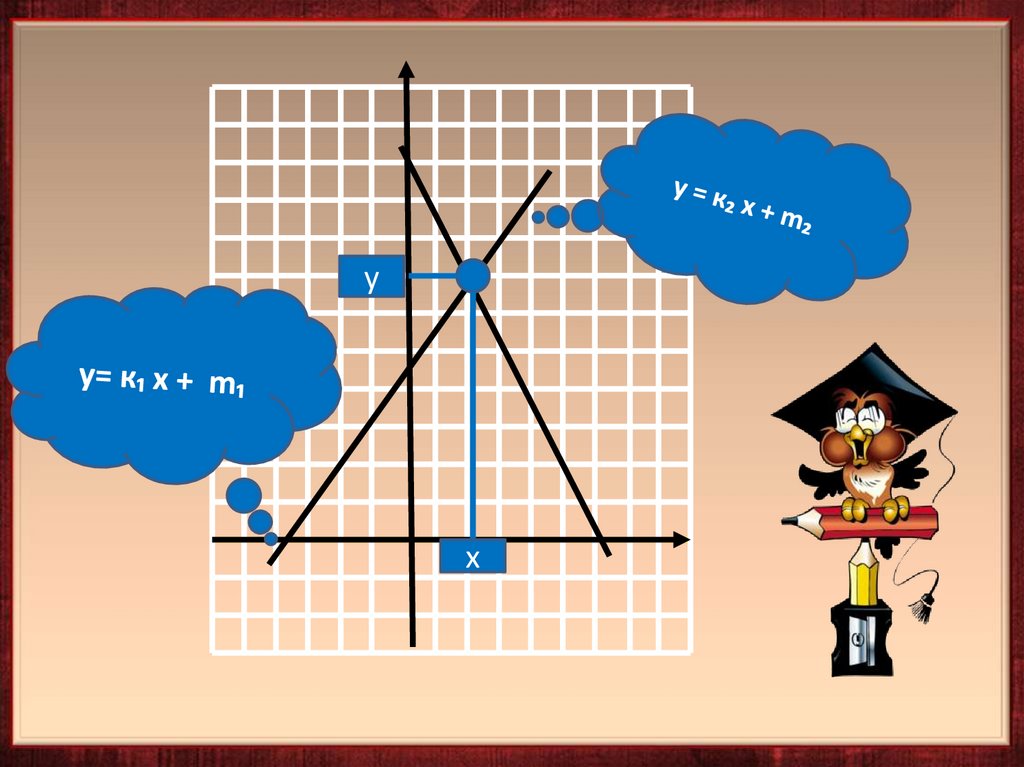
Графический способ (алгоритм)• Выразить у через х в каждом уравнении
• Выяснить сколько решений имеет
система
• Построить в одной системе координат
график каждого уравнения
• Определить координаты точки
пересечения
• Записать ответ (х; у)
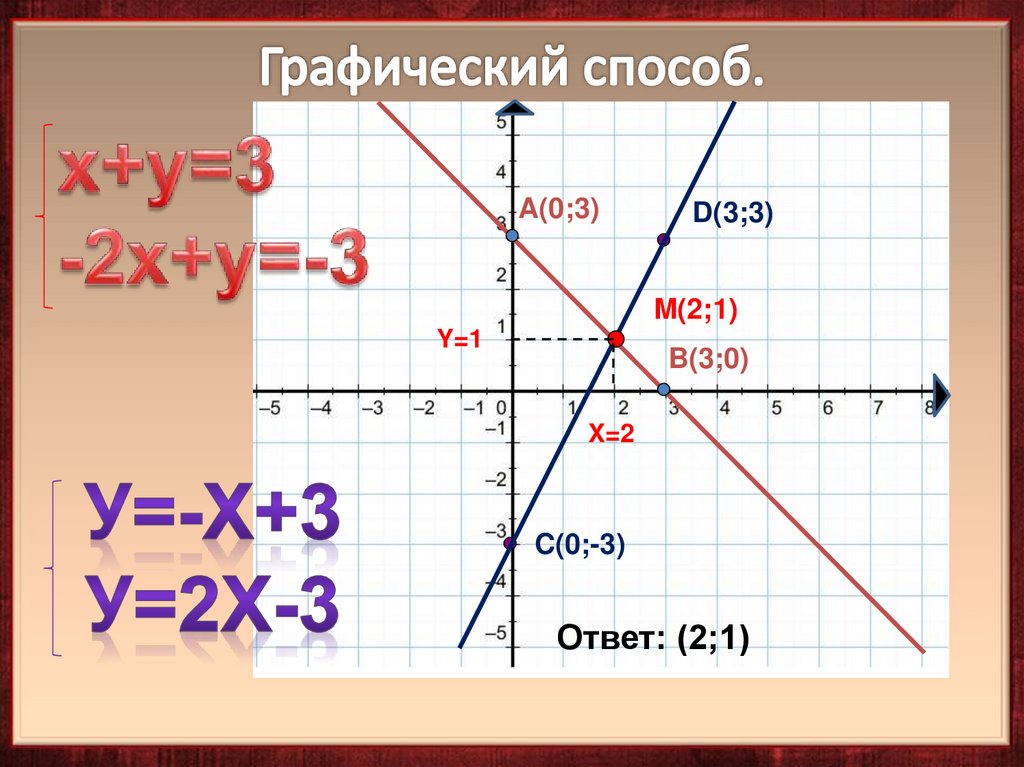
12. Графический способ.
A(0;3)D(3;3)
M(2;1)
Y=1
B(3;0)
X=2
C(0;-3)
Ответ: (2;1)
13.
Способподстановки ( алгоритм )
• Из какого-либо уравнения выразить
одну переменную через другую
• Подставить полученное выражение для
переменной в другое уравнение и
решить его
• Сделать подстановку найденного
значения переменной и вычислить
значение второй переменной
• Записать ответ: ( х ; у )
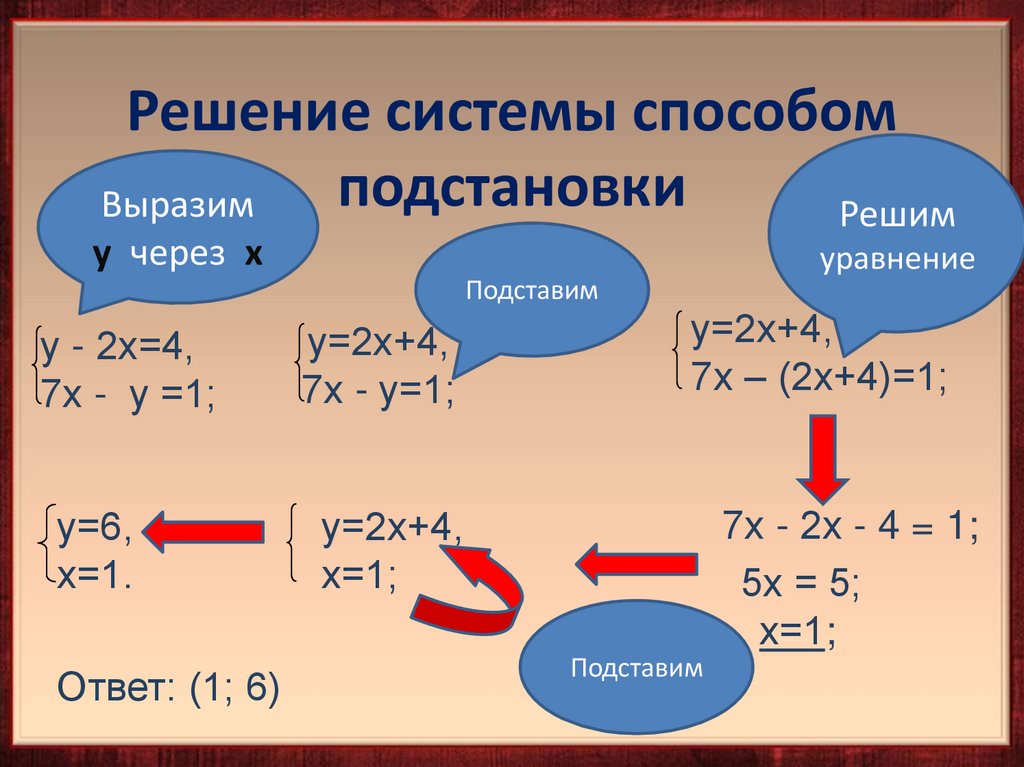
14.
Решение системы способомподстановки
Выразим
Решим
у через х
уравнение
Подставим
у - 2х=4,
7х - у =1;
у=2х+4,
7х - у=1;
у=6,
х=1.
у=2х+4,
х=1;
Ответ: (1; 6)
у=2х+4,
7х – (2х+4)=1;
7х - 2х - 4 = 1;
5х = 5;
х=1;
Подставим
15. Способ сложения (алгоритм)
• Уравнять модули коэффициентов при какойнибудь переменной• Сложить почленно уравнения системы
• Решить новое уравнение и найти значение
одной переменной
• Подставить значение найденной
переменной в старое уравнение и найти
значение другой переменной
• Записать ответ: ( х ; у ).
16. Решение системы способом сложения
7х+2у=1,|·( -3)17х+6у=-9;
+
-21х-6у=-3,
17х+6у=-9;
-----------------21х + 17х = -3 - 9
Ответ: (3; - 10)
- 4х = - 12,
х=3;
х=3,
х=3,
х=3,
7·3+2у=1; 21+2у=1; 2у=-20;
х=3,
у=-10.
17.
18. «Чтобы решить вопрос, относящийся к числам или к отвлеченным отношениям величин, нужно лишь перевести задачу с родного языка на
19.
Как-то лошадь и мул вместе вышли из домаИх хозяин поклажей большой нагрузил.
Долго-долго шли дорогой знакомой,
Из последних уже выбиваяся сил.
«Тяжело мне идти»,-лошадь громко стонала.
Мул с иронией молвил (нес он тоже немало).
«Неужели скажи я похож на осла?
Может я и осел, но вполне понимаю:
Моя ноша значительно больше твоей.
Вот представь:я мешок
у тебя
забираю
я мешок
у тебя
забираю,
И мой
раза
чемчем
твой,
тяжелей.
мойгруз
грузстал
сталв два
в два
раза
твой,
тяжелей
вотесли
еслитебе
тебемой
мой
мешок
перебросить
А вот
мешок
перебросить,
Одинаковый
груз
наши
спины
б согнул».
Одинаковый груз
наши
спины
б согнул».
Сколько ж было мешков у страдалицы- лошади?
Сколько нес на спине умный маленький мул?
20. Решение
Две неизвестныевеличины
Было
Стало, когда мул
забрал мешок
Стало, когда мул
отдал мешок
Поклажа,
которую несла
лошадь
х
х-1
х+1
Поклажа, которую
нес мул
у
у+1
у-1
1-е уравнение: 2(х-1)=у+1
Полученная система
уравнений:
2-е уравнение: х+1=у-1
2(х-1)=у+1
х+1=у-1
21.
22. Алгоритм решения задачи с помощью системы уравнений:
• Ввести обозначения неизвестных исоставить систему уравнений;
• Решить систему уравнений;
• Возвратиться к условию задачи и
использованным обозначениям,
записать ответ.
23.
24. Домашнее задание:
1 Задача иранского ученого XVI векаБехаэддина
2. Задача Бхаскары
3. Задача Ал – Хорезми
4. Задача из книги «Математика в девяти
книгах»
5. Задача из рассказа А.П.Чехова
«Репетитор»





















 mathematics
mathematics








