Координатный метод (ключевые задачи). Готовимся к ЕГЭ

1. Готовимся к ЕГЭ. Задача С2. Координатный метод (ключевые задачи).

МБОУ г. Мурманска гимназия №3
Шахова Татьяна Александровна

2.

Координатный метод может быть использован
для нахождения:
1)
2)
3)
4)
5)
6)
7)
длины отрезка (расстояния между точками);
расстояния между прямыми;
расстояния от точки до прямой и плоскости;
угла между прямыми;
угла между прямой и плоскостью;
угла между плоскостями;
нахождения площади сечения.
Первоначальные сведения
о прямоугольной системе координат
смотри по адресу:
http://le-savchen.ucoz.ru/load/4-1-0-183

3.

Ключевые задачи.
1) Нахождение координат точки.
2) Нахождение угла между прямыми.
3) Вывод уравнения плоскости.
4) Нахождение расстояния от точки до плоскости.
5) Нахождение угла между плоскостями.
6) Нахождение угла между прямой и плоскостью.
7) Нахождение расстояния между прямыми.

4.

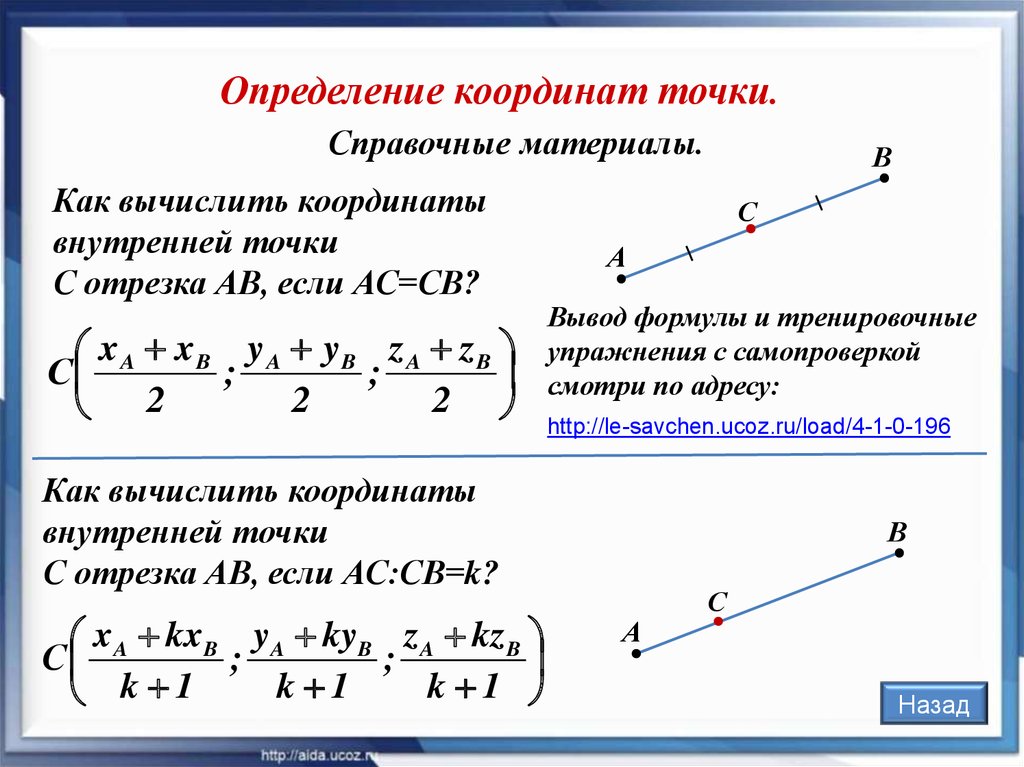
Определение координат точки.
Справочные материалы.
Как вычислить координаты
внутренней точки
С отрезка АВ, если АС=СВ?
x A xB y A yB z A z B
С
;
;
2
2
2
С
А
Вывод формулы и тренировочные
упражнения с самопроверкой
смотри по адресу:
http://le-savchen.ucoz.ru/load/4-1-0-196
Как вычислить координаты
внутренней точки
С отрезка АВ, если АС:СВ=k?
x A kxB yA kyB z A kz B
С
;
;
k 1
k 1
k 1
В
В
А
С
Назад

5.

Определение координат точки.
Тренировочные упражнения.
Прямоугольный параллелепипед
Правильная шестиугольная призма
Правильная четырехугольная пирамида
Правильная треугольная пирамида

6.

Определение координат точки.
ABCDA1B1C1D1 – прямоугольный параллелепипед. AB=2,
AD=4, AA1=2, А1К=КВ1, АМ:МС=2:3, KL=LM .
Определите координаты точек A, C, А1, В1, К, М, L.
Z
С1
D1
К
А1
2
X
Задачи
C(?;?;?)
C(0;2;0)
B1(?;?;?) B1(4;2;2)
К(?;?;?) К(4;1;2)
M(?;?;?) ?
x kxC y A kyC z A kzC
M A
;
;
k 1
k 1
k 1
Y
М
А
А1(?;?;?) А1(4;0;2)
С
D
4
А(4;0;0)
В1
L
2
А(?;?;?)
В
2
2
2
4
0
0
2
0
0
3 ;
3 ;
3 12 ; 4 ;0
2
2
2 1
5
5
1
1
3
3
3

7.

Определение координат точки.
ABCDA1B1C1D1 – прямоугольный параллелепипед. AB=2,
AD=4, AA1=2, А1К=КВ1, АМ:МС=2:3, KL=LM .
Определите координаты точек A, C, А1, В1, К, М, L.
Z
К(4;1;2)
С1`
D1
L(?;?;?) ?
К
А1
С
D
4
2
X
Задачи
Y
М
А
xK xM yK yM z K zM
L
;
;
2
2
2
В1
L
2
12 4
M ; ;0
5 5
В
12
4
1
4
2 0
5
5
;
;
2
2
2
22 9
; ;1
10 10

8.

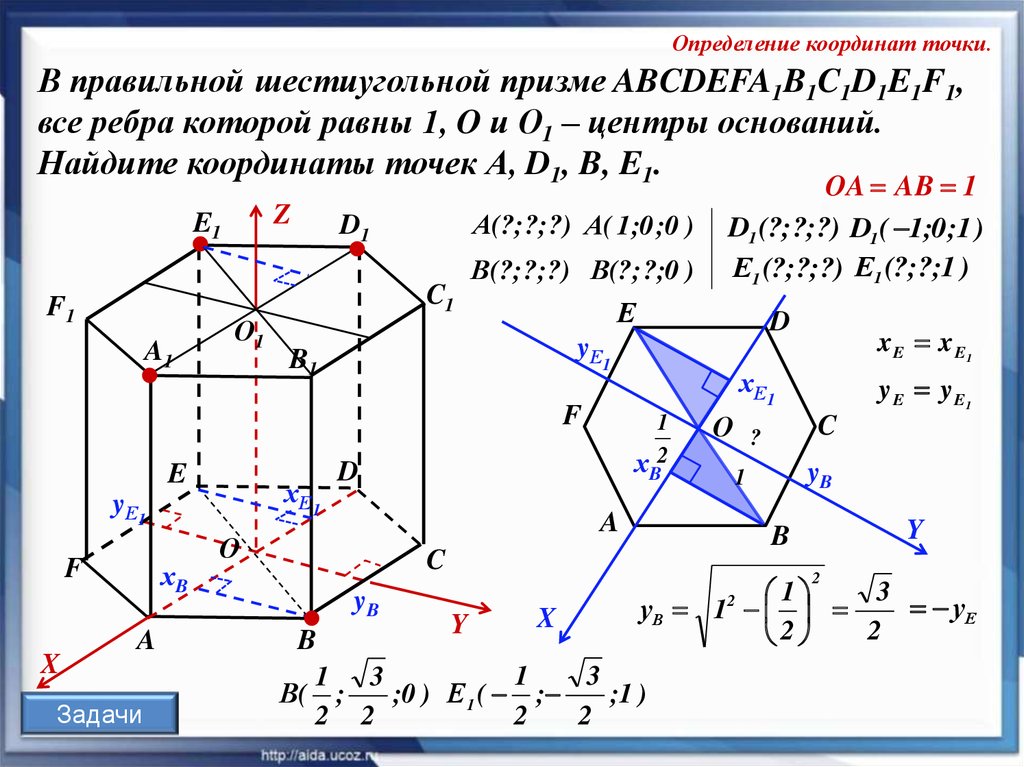
Определение координат точки.
В правильной шестиугольной призме ABCDEFA1B1C1D1E1F1,
все ребра которой равны 1, O и О1 – центры оснований.
Найдите координаты точек А, D1, B, E1.
Z
E1
F1
A1
О1
А(?;?;?) А( 1 ;0 ;0 )
D1
C1
В(?;?;?) В(?; ?;0 )
Е
D
yЕ1
B1
хЕ 1
yЕ1
F
X
хB
A
Задачи
1
2
хB
D
A
О
C
yB
x E x E1
хЕ 1
F
E
OA AB 1
D1 (?;?;?) D1 ( 1;0 ;1 )
Е1 (?;?;?) Е1 (?;?;1 )
О ?
y E y E1
C
yB
1
Y
B
2
Y
X
3
1
уЕ
уВ 12
2
2
B
1
3
1 3
В( ;
;0 ) Е 1 ( ;
;1 )
2
2
2 2

9.

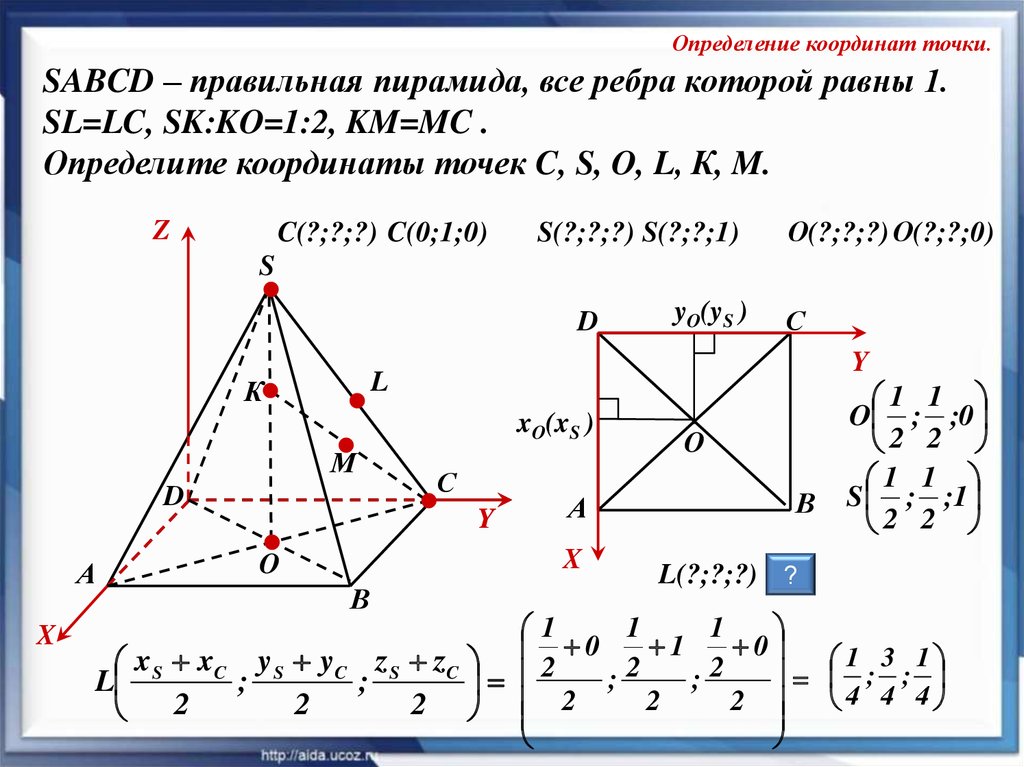
Определение координат точки.
SABCD – правильная пирамида, все ребра которой равны 1.
SL=LC, SK:KO=1:2, KM=MC .
Определите координаты точек C, S, O, L, К, M.
Z
C(?;?;?) C(0;1;0)
S(?;?;?) S(?;?;1)
О(?;?;?) О(?;?;0)
S
D
Y
xO(xS )
М
D
X
С
L
К
А
yO(yS )
С
Y
А
X
O
В
O
В
1 1
O ; ;0
2 2
1 1
S ; ;1
2 2
L(?;?;?) ?
1
1
1
0
1
0
1 3 1
x S xC y S yC z S zC 2
2
2
; ;
;
;
L
;
;
4 4 4
2
2
2
2
2 2

10.

Определение координат точки.
SABCD – правильная пирамида, все ребра которой равны 1.
SL=LC, SK:KO=1:2, KM=MC .
Определите координаты точек C, S, O, L, К, M.
Z
1 1 O 1 ; 1 ;0
S ; ;1
2 2
2 2
S
K(?;?;?) ?
L
К
М
D
А
X
Задачи
x S kxO y S kyO z S kzO
K
;
;
k 1
k 1
k 1
С
Y
O
1
1 1 1 1 1 1
1
0
В
2 1 ;1 ;2
2 2 2 ;2 2 2 ;
1
1
1 1
2
2
3
1
1
2
2
2

11.

Определение координат точки.
SABCD – правильная пирамида, все ребра которой равны 1.
SL=LC, SK:KO=1:2, KM=MC .
Определите координаты точек C, S, O, L, К, M.
Z
1 1 2
K ; ;
2 2 3
S
C(0;1;0)
M(?;?;?) ?
L
К
М
D
А
X
Задачи
xC x K yC y K zC z K
M
;
;
2
2
2
С
Y
O
В
2
1
1
0
0
1
1 3 1
3
2
2
; ;
;
;
2
2 4 4 3
2

12.

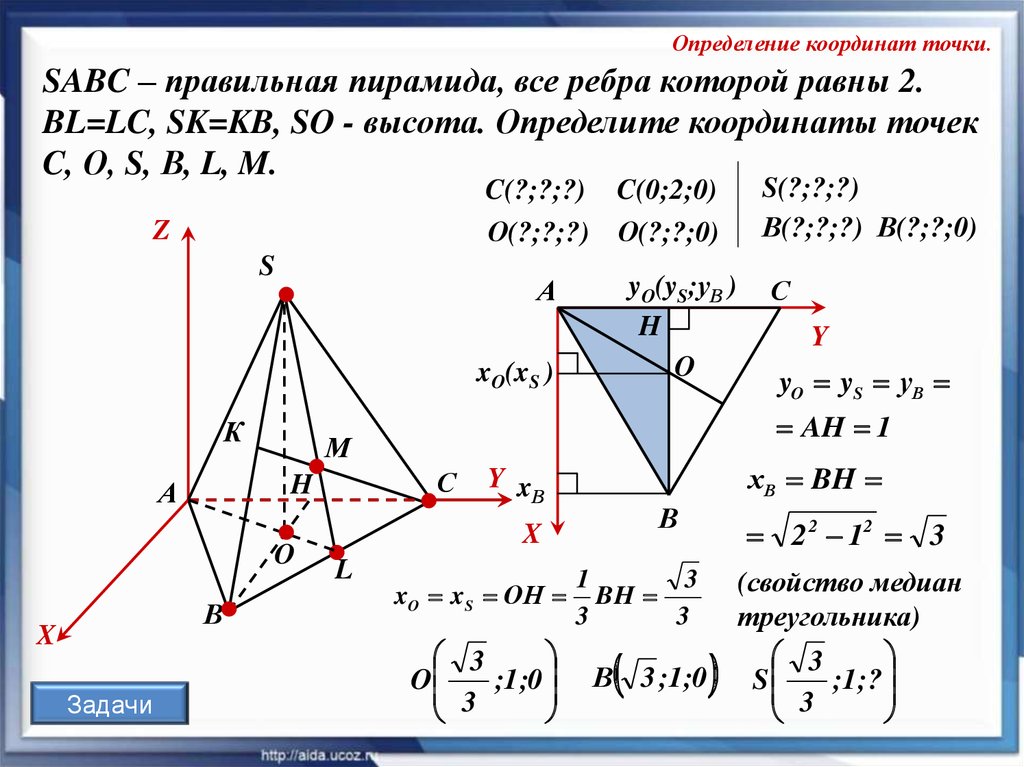
Определение координат точки.
SABC – правильная пирамида, все ребра которой равны 2.
BL=LC, SK=KB, SO - высота. Определите координаты точек
C, О, S, В, L, M.
C(?;?;?) C(0;2;0)
О(?;?;?) О(?;?;0)
Z
S
yO(yS;уВ )
H
O
А
xO(xS )
К
O
В
X
Задачи
С
Y
yO yS уВ
хВ BH
Y x
В
В
X
L
С
AH 1
М
H
А
S(?;?;?)
В(?;?;?) В(?;?;0)
xO xS ОН
3
O
;1 ;0
3
2 2 12 3
1
3
BH
3
3
В 3 ;1;0
(свойство медиан
треугольника)
3
S
;1 ;?
3

13.

Определение координат точки.
SABC – правильная пирамида, все ребра которой равны 2.
BL=LC, SK=KB, SO - высота. Определите координаты точек
C, О, S, В, L, M.
3
S
;1 ;?
3
Z
S
ВО
BH 3
zS SO
2
2 3
ВН
3
3
Из треугольника ВОS
К
С
А
O
В
X
Задачи
2
М
Y
X
L
2 3
2 6
z S SO 2
3
3
2
3
2 6
S
;1 ;
3
3

14.

Определение координат точки.
SABC – правильная пирамида, все ребра которой равны 2.
BL=LC, SK=KB, SO - высота. Определите координаты точек
C, О, S, В, L, M.
C(0;2;0)
Z
B
3 ;1;0
S
L(?;?;?) (середина отрезка ВС) ?
x xC yB yC z B zC
L B
;
;
2
2
2
К
М
С
А
O
В
X
Задачи
Y
X
L
3 0 1 2 0 0
;
;
2
2
2
3 3
L
; ;0
2 2

15.

Определение координат точки.
SABC – правильная пирамида, все ребра которой равны 2.
BL=LC, SK=KB, SO - высота. Определите координаты точек
C, О, S, В, L, M.
3
2 6
S
;1 ;
3
3
Z
S
3 3
L
2 ; 2 ;0
М(?;?;?)
К
М
С
А
O
В
X
Задачи
М – точка пересечения медиан
треугольника BSC => SМ:ML=2:1 ?
Y
X
L
x S kx L y S ky L z S kz L
M
;
;
k 1
k 1
k 1
3
3
3 2 6
2
2 0 4 3 4 2 6
1 2
2 ;
2; 3
; ;
3
2 1
2 1
2 1 9 3 9

16.

Нахождение угла между прямыми.
Алгоритм.
1 ) АВ xB x A ; yB yA ; zB z A
СD x D xC ; yD yC ; z D zC
направляющие векторы
D
2 ) АВ CD x x y y z z
AB
CD
AB
CD
3)
С
2
2
AB
AB
AB
В
CD
А
АВ x y z
2
AB
CD x 2 y2 z 2
CD
CD
CD
AB CD
4 ) cos ( AB; CD )
AB CD
Назад

17.

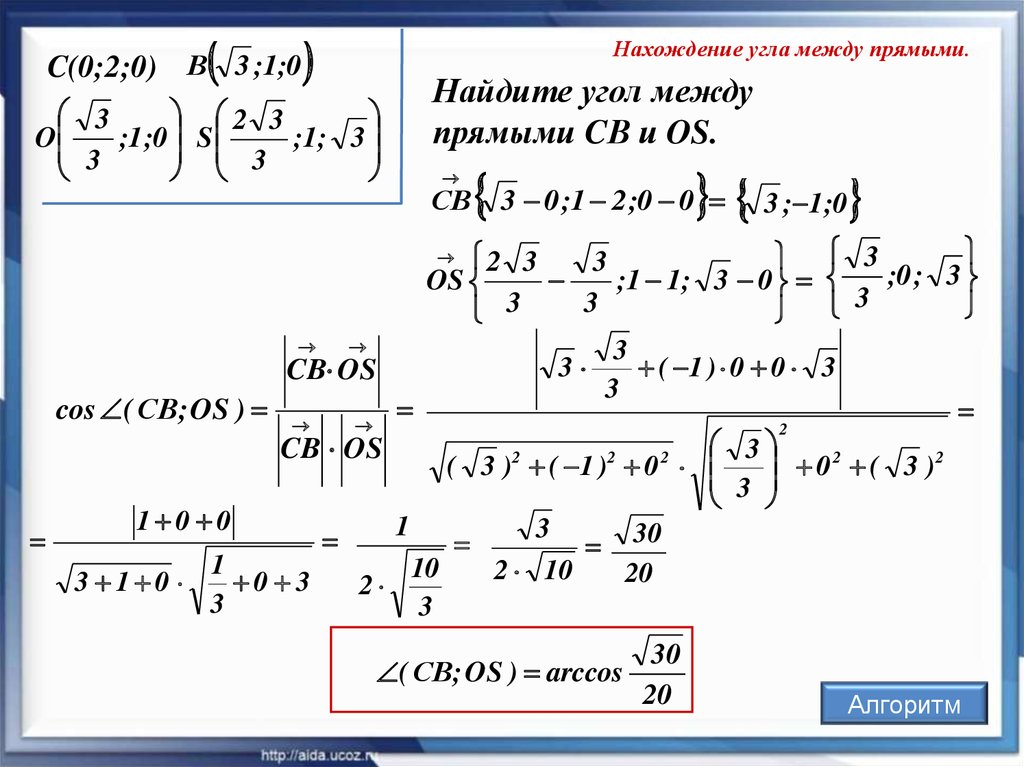
C(0;2;0) В 3 ;1;0
Нахождение угла между прямыми.
Найдите угол между
прямыми CВ и OS.
3
2 3
O
;1 ;0 S
;1; 3
3
3
СВ
3 0 ;1 2;0 0 3 ; 1;0
2 3
3
OS
;1 1; 3 0
3
3
3
3
( 1 ) 0 0
3
CB OS
cos ( СB; OS )
3
3
0 2 ( 3 )2
( 3 ) ( 1 ) 0
3
1 0 0
1
3
30
1
10
2 10
20
3 1 0
0 3
2
3
3
CB OS
2
3
;0 ; 3
3
2
2
( СB; OS ) arccos
2
30
20
Алгоритм

18.

Вывод уравнения плоскости ax+by+cz+d=0.
Алгоритм.
1) Подставить в уравнение плоскости
координаты точек А,В и С.
А
В
ax A byA cz A d 0
ax B byB cz B d 0
ax by cz d 0
C
C
C
С
2) Решить систему - выразить а, b и с через d; либо а, b и d через с;
либо а, с и d через b, либо c, b и d через a в зависимости от
составленной системы.
3) Подставить выраженные коэффициенты в исходное
уравнение и преобразовать к удобному виду.
Назад

19.

А 3;1;1
В 3;1;3
С 2;3;2
Вывод уравнения плоскости.
Запишите уравнение плоскости (АВС)
3a b c d 0
2с 0 с 0
3a b 3c d 0
2 a 3b 2 c d 0
3a b d 0
а 2b 0 a 2b
2 a 3b d 0
ax by cz d 0
2 bx by 0 z 7 b 0 b
2x y 7 0
6 b b d 0 7 b d 0 d 7 b
Алгоритм

20.

Вывод уравнения плоскости.
1 3 1 3
;0
А ;
;0 С ;
Запишите уравнение плоскости (АВС)
2 2
2 2
В 1;0 ;1
1
3
a
b 0 c d 0
3
2
2
3b 2 d 0 d
b
2
1
3
b 0 c d 0
a
2
2
1 a 0 b 1 c d 0
ax by cz d 0
3
3
0 x by
bz
b 0
1
3
3
2
2
a
b
b 0 a 0
2
2
2
3
3
y
z
0 2
3
2
2
c
b 0 c 3 b
2
2
2 y 3z 3 0
b
Алгоритм

21.

Нахождение расстояния от точки до плоскости.
Алгоритм.
А
Если плоскость α задана уравнением
ax by cz d 0 ,
то расстояние от точки А до
плоскости α можно найти
по формуле:
( A; )
α
ax A byA cz A d
a2 b2 c 2
Назад

22.

: 2 x 3 y 3z 3 0
1 3
А ;
; 2
2 2
2
( A; )
Расстояние от точки плоскости.
Найдите расстояние от точки А
до плоскости α.
1
3
3
3 ( 2 ) 3
2
2
2 2 ( 3 )2 ( 3 )2
1
3
2 3 3
2
4 3 3
5
3 3
3 3 2 ,5
2
10
10
Алгоритм

23.

Нахождение угла между плоскостями.
Алгоритм.
α
Если плоскости α и β заданы уравнениями
a1 x b1 y c1z d1 0 и a2 x b2 y c2 z d2 0
β
соответственно, то
a a1 ; b1 ; c1 - вектор нормали (перпендикуляра) плоскости α,
b a2 ; b2 ; c2 - вектор нормали плоскости β.
Угол между плоскостями равен углу
между нормалями этих плоскостей.
cos ( ; ) cos ( a ; b )
Алгоритм
Назад

24.

Угол между плоскостями.
: 2 x 3 y 3z 3 0
Найдите угол между плоскостями α и β.
: x 2 3 y 3z 7 0
b 1;2
a 2; 3 ; 3
3 ; 3
- нормали плоскостей α и β.
a b
cos ( ; )
a b
2 6 3
4 3 3 1 3 3
2 1 3 2 3 3 ( 3 )
2 ( 3 ) ( 3 ) 1 ( 3 ) ( 3 )
2
2
5
10 7
( ; ) arccos
2
2
2
2
5
5 70
70
70
14
70
70
14
Алгоритм

25.

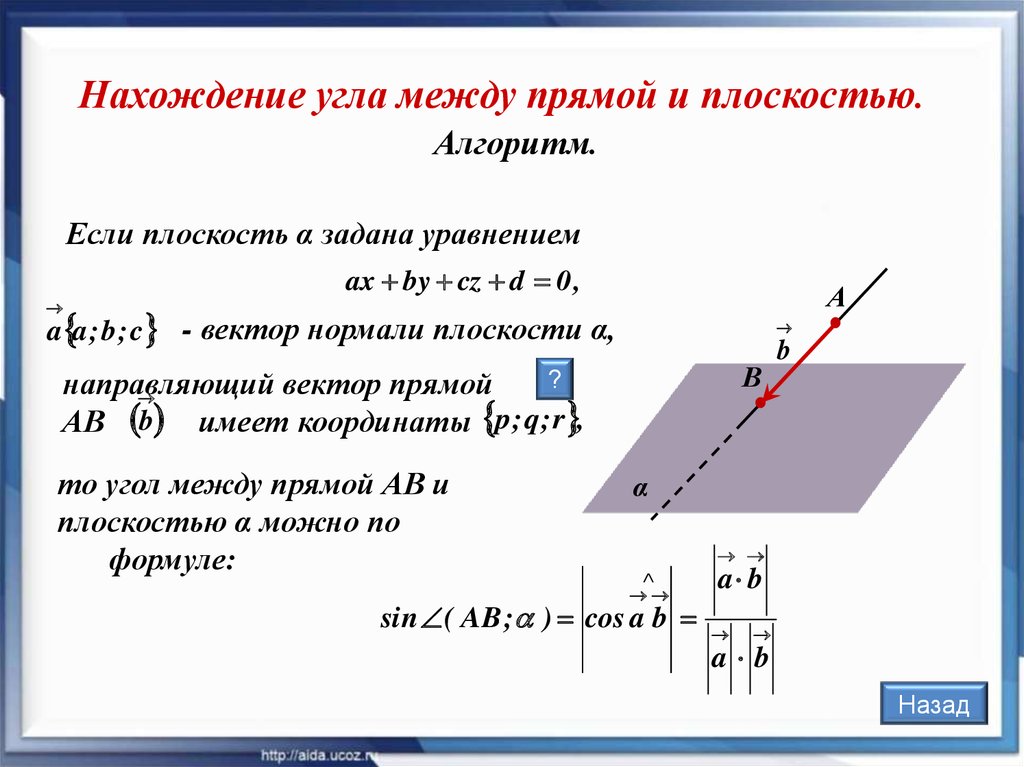
Нахождение угла между прямой и плоскостью.
Алгоритм.
Если плоскость α задана уравнением
ax by cz d 0 ,
А
a a ; b ; c - вектор нормали плоскости α,
В
?
направляющий
вектор прямой
АВ b имеет координаты p; q; r ,
то угол между прямой АВ и
плоскостью α можно по
формуле:
b
α
sin ( AB ; ) cos a b
a b
a b
Назад

26.

Угол между прямой и плоскостью.
: 2 x 3 y 3z 3 0
А 3; 1; 1 В 3;1;3
a 2; 3 ; 3
Найдите угол между плоскостямью α
и прямой АВ.
- вектор нормали плоскости α
AB 3 3 ;1 ( 1 ); 3 ( 1 ) 0 ;2;4 - направляющий вектор прямой АВ
a b
sin
a b
2 0 2 3 4 3
2 ( 3 ) ( 3 ) 0 2 4
2
2
6 3
4 3 3 0 4 16
2
2
2
2
6 3
6 3
6 3
3 3 3 6
10
10 20
200 10 2 5 2
( ; AB ) arcsin
3 6
10
Алгоритм

27.

Нахождение расстояния между прямыми.
Алгоритм.
1) Определить координаты
М
направляющих векторов AB и CD .
B
Пусть MK AB , CD , тогда
выполнено
AB MK 0
C
условие: CD MK 0.
К
2) Из системы определить
координаты MK , затем найти MK ( a ; b )
А
a
b
D
Замечание: для записи координат точек М и К воспользоваться
формулой:
x A kx B y A kyB z A kz B
;
;
k 1
k 1
k 1
Если АМ:МВ=k, то M
Назад

28.

A 0 ;0 ;0 В 0 ;1;0
С 0 ;1;1 D 1;0 ;1
Нахождение угла между прямыми.
Найдите расстояние между
C
прямыми AC и BD.
М
AC 0 0 ;1 0 ;1 0 0 ;1;1
B
А
К
BD 1 0 ;0 1;1 0 1; 1;1
Пусть MK AB, CD, АМ:МС=k, BK:KD=n, тогда:
k
k
x A kxC yA kyC z A kzC
;
M
;
;
0;
k 1
k 1 k 1 k 1
k 1
x nxD yB nyD z B nzD
K B
;
;
n 1
n 1
n 1
1
n
n
;
;
n
1
n
1
n
1
D
k
p
k 1
Если
n
q,
n 1
то M 0 ; p; p , K q;1 q; q , MK q ;1 q p ; q p .
AС MK 0 0 q 1 ( 1 q p ) 1 ( q p ) 0
MK AB, CD
BD MK 0. 1 q ( 1 ) ( 1 q p ) 1 ( q p ) 0.
Алгоритм

29.

A 0 ;0 ;0 В 0 ;1;0
С 0 ;1;1 D 1;0 ;1
Нахождение угла между прямыми.
Найдите расстояние между
C
прямыми AC и BD.
М
MK q ;1 q p ; q p
B
0 q 1 ( 1 q p ) 1 ( q p ) 0
1 q ( 1 ) ( 1 q p ) 1 ( q p ) 0.
1 q p q p 0
q 1 q p q p 0
1 2 p 0
1 3q 0
1 1 1
1
MK ;1 ;
3 2 3
3
1 1 ; 1 ; 1
2 3 6 6
2
2
D
1
p
1 2 p 0
2
1 3q 0
1
q
3
2
1 1 1
MK ( AC ; BD )
3 6 6
А
1
1
9
81
Алгоритм

30.

При создании презентации использовано
пособие:
http://www.alleng.ru/d/math/math784.htm
15.04.2017
30