Проецирование прямых

1. Урок 11 – Проецирование прямых

Проецирование
прямых
прямые общего положения
прямые частного положения
плоскости
Взаимное положение прямых в
пространстве

2. Проецирование прямой на 1 плоскость

В
А
А1
В1
1
Вывод: проекция прямой – прямая.

3. Проецирование прямой на 1 плоскость (обратная задача)

А1
1
В1
Вывод: для определения положения прямой в
пространстве
одной
ее
проекции
недостаточно.

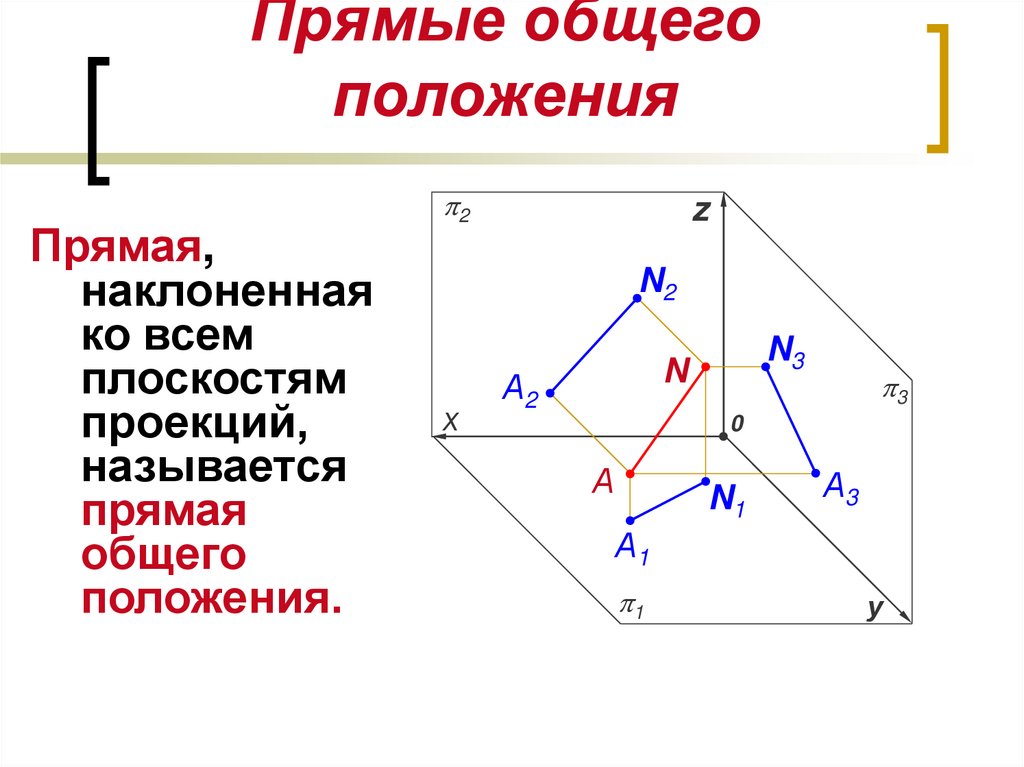
4. Прямые общего положения

Прямая,
наклоненная
ко всем
плоскостям
проекций,
называется
прямая
общего
положения.
2
z
N2
х
N3
N
А2
3
0
А
N1
А3
А1
1
у

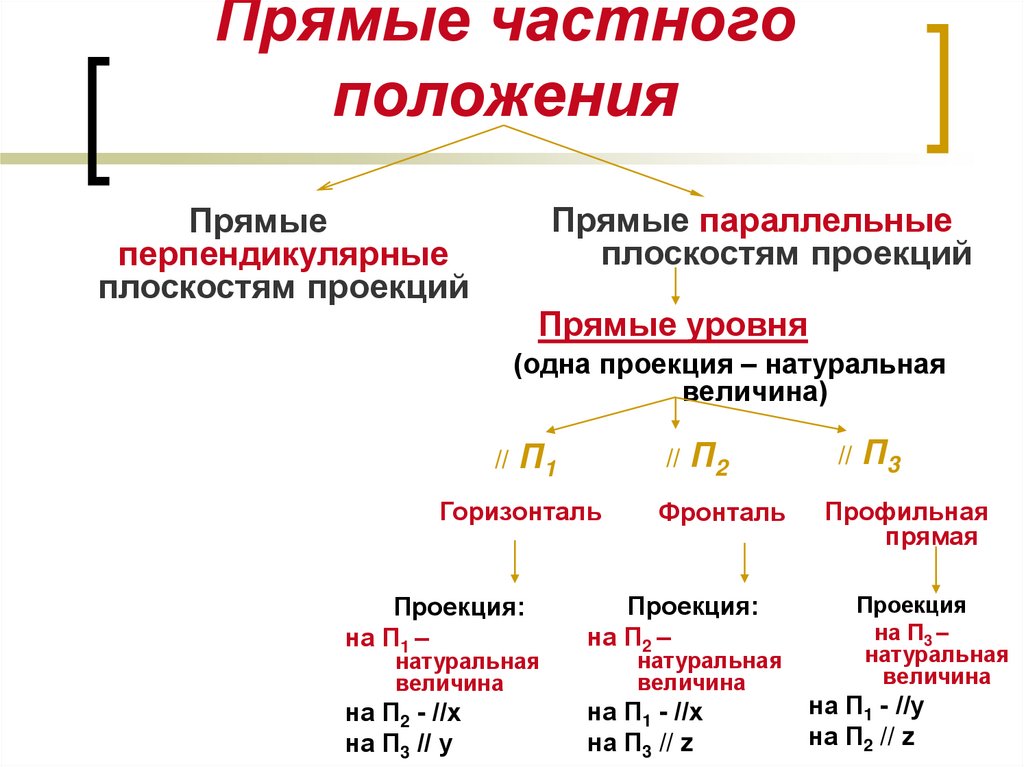
5. Прямые частного положения

Прямые
перпендикулярные
плоскостям проекций
Проецирующие
прямые
(одна проекция есть
точка)
/ П3
/ П2
/ П1
Прямые параллельные
плоскостям проекций
Горизонтально- Фронтально- Профильнопроецирую
проецирую
проецирую
щие
щие
щие
Проекция:
на П1 –
точка
на П2//z
на П3//z
Проекция:
на П2 – точка
на П1//у
на П3//у
Проекция:
на П3 – точка
на П1//х
на П2//х

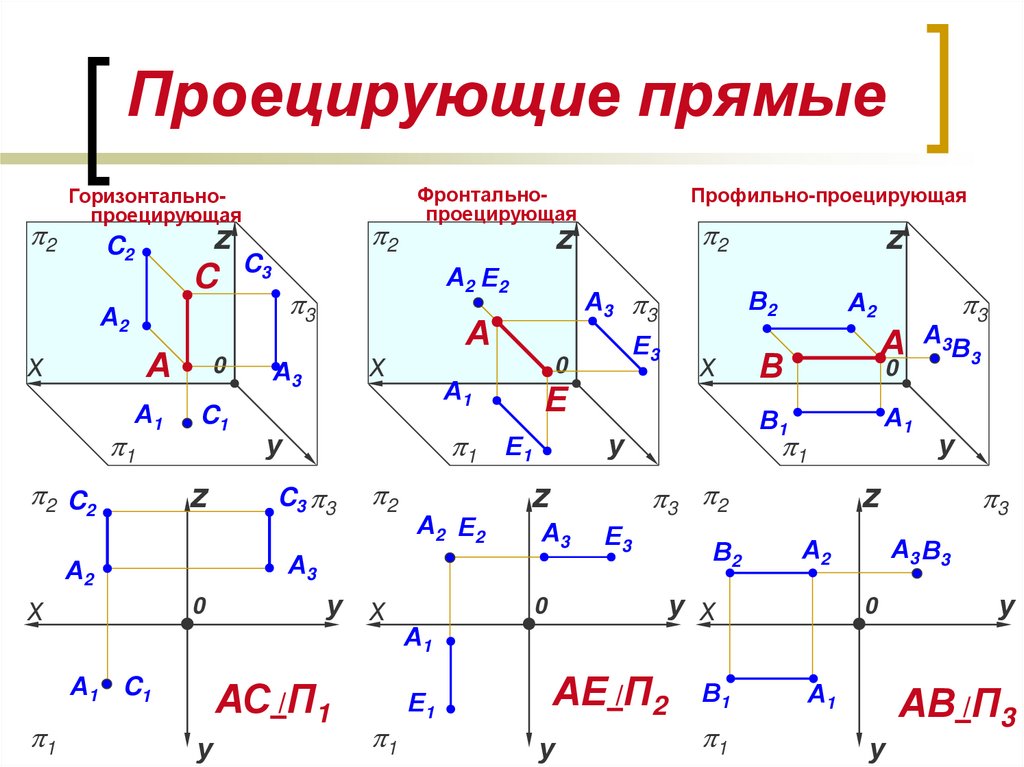
6. Проецирующие прямые

2
Горизонтальнопроецирующая
z
C
C2
2
C3
х
А
А1
1
2 C2
C1
z
0
А1 C1
1
х
у х
АС /П1
у
Е
1 Е1
2
А2 Е2
1
Е3
0
А1
у
C3 3
2
А3 3
А
А3
А2
х
А2 Е2
А3
Профильно-проецирующая
z
3
А2
0
Фронтальнопроецирующая
х
А2
А
В
А1
1
3 2
z
Е3
В2
АЕ /П2
у
В1
1
3
В3
у
3
z
А3 В3
А2
у х
А1
А3
0
В1
0
Е1
В2
у
А3
z
0
А1
у
у
АВ /П3

7. Прямые частного положения

Прямые параллельные
плоскостям проекций
Прямые
перпендикулярные
плоскостям проекций
Прямые уровня
(одна проекция – натуральная
величина)
//
П1
//
Горизонталь
П2
Фронталь
Проекция:
на П1 –
Проекция:
на П2 –
на П2 - //х
на П3 // у
на П1 - //х
на П3 // z
натуральная
величина
натуральная
величина
//
П3
Профильная
прямая
Проекция
на П3 –
натуральная
величина
на П1 - //у
на П2 // z

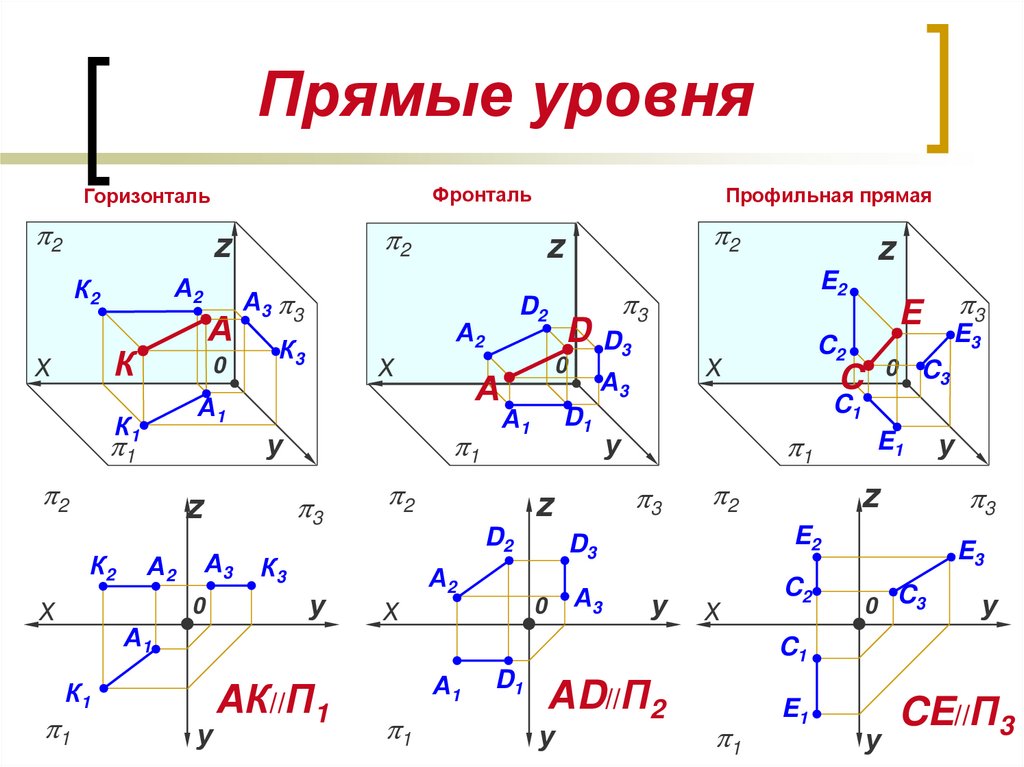
8. Прямые уровня

Фронталь
Горизонталь
2
2
z
А2
К2
А
К
х
0
А3 3
К3
А1
К1
1
3
z
х
А2
А3
0
у
А1
А2
А
А1
х
0
C3
E1
у
C
1
у
3
А3
0
E3
C1
2
3
z
E2
D3
А2
C2
х
А3
z
3
E
D3
D1
D2
E2
3
D
0
z
у
х
C2
E3
0 C3
у
C1
К1
1
D2
2
К3
2
z
1
у
2
К2
х
Профильная прямая
у
АК//П1
А1
1
D1
АD//П2
у
1
E1
у
CE//П3

9. Практическое задание №1

Определить положение прямых а, в, с, h, f, l,
m, p в пространстве.
а / П3
с – общ.
в / П2
положение
h // П1
f // П2
m – общ.
положение
l / П1
p // П3

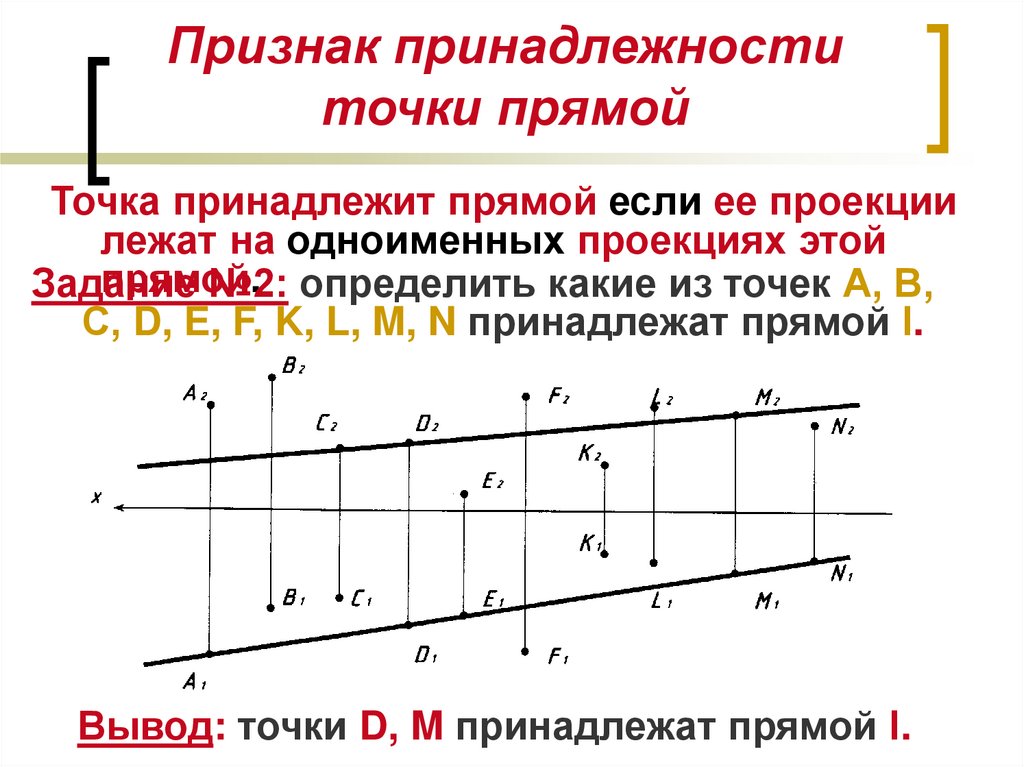
10. Признак принадлежности точки прямой

Точка принадлежит прямой если ее проекции
лежат на одноименных проекциях этой
прямой.
Задание
№2: определить какие из точек А, В,
С, D, E, F, K, L, M, N принадлежат прямой l.
Вывод: точки D, M принадлежат прямой l.

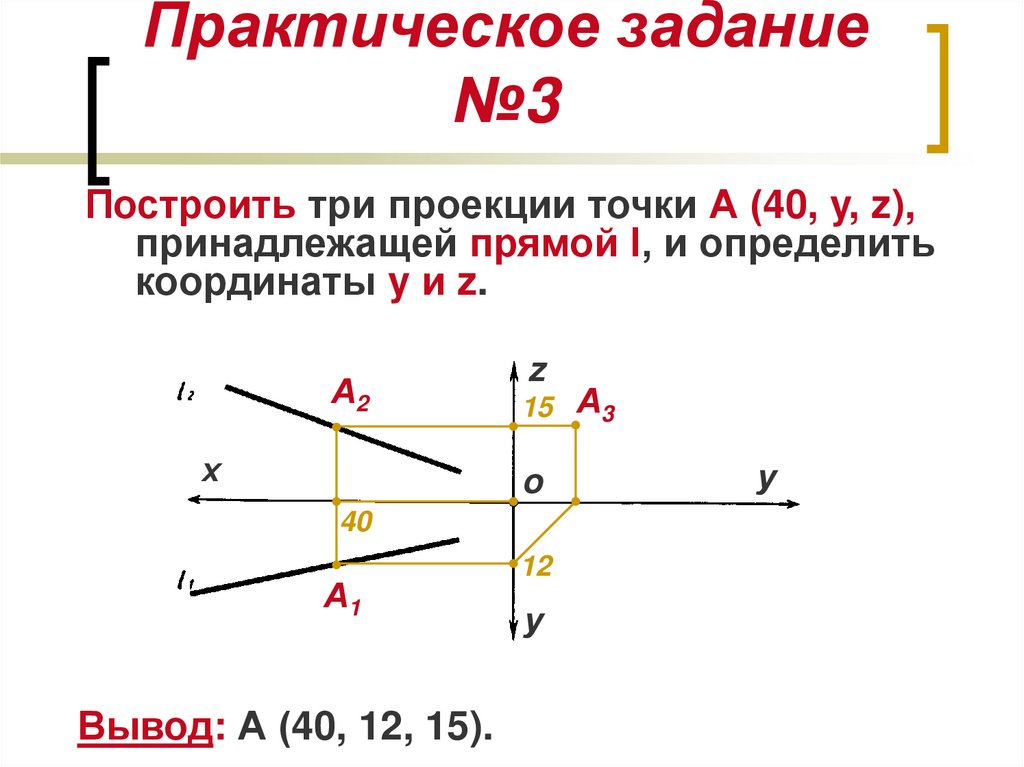
11. Практическое задание №3

Построить три проекции точки А (40, y, z),
принадлежащей прямой l, и определить
координаты y и z.
А2
х
z
15 А3
o
40
А1
Вывод: А (40, 12, 15).
12
у
у

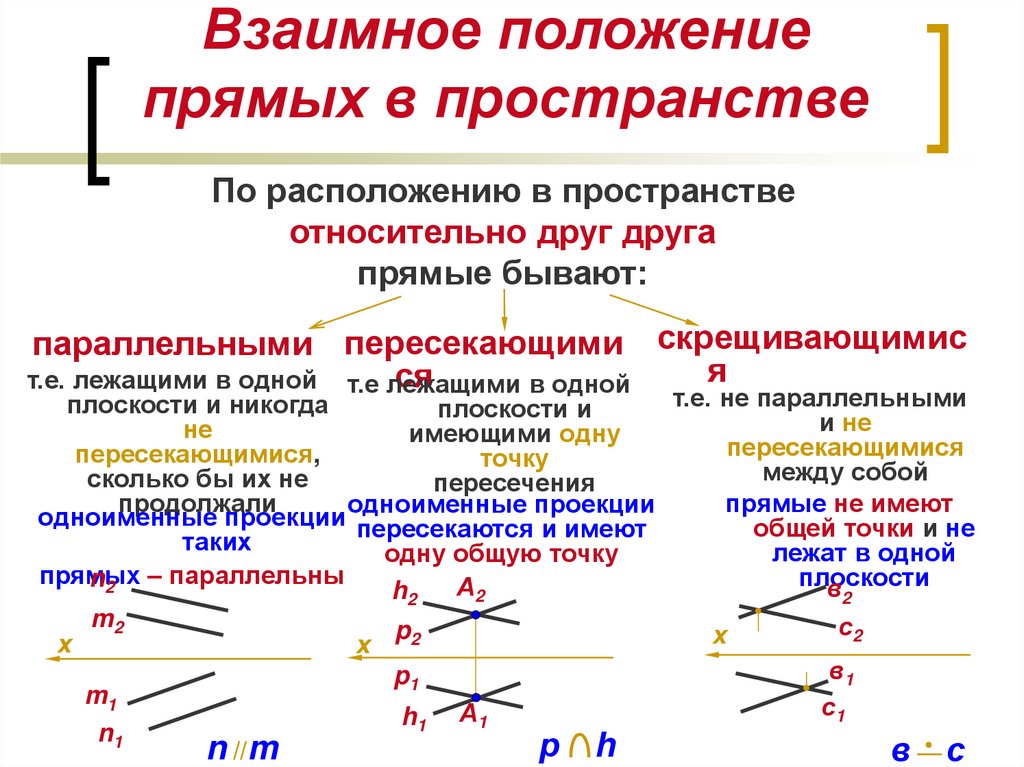
12. Взаимное положение прямых в пространстве

По расположению в пространстве
относительно друг друга
прямые бывают:
параллельными пересекающими скрещивающимис
я
ся
т.е. лежащими в одной т.е лежащими
в одной
т.е. не параллельными
плоскости и никогда
плоскости и
и не
не
имеющими одну
пересекающимися
пересекающимися,
точку
между собой
сколько бы их не
пересечения
продолжали
прямые не имеют
проекции
одноименные проекции одноименные
общей точки и не
пересекаются и имеют
таких
лежат в одной
одну общую точку
прямых
плоскости
n2 – параллельны
А2
в2
h2
m2
с2
p2
х
х
х
в1
p1
m1
с1
h1 А1
n1
р h
n //m
в с

13. Конкурирующие точки

Конкурирующие точки – это точки, у которых одна
проекция совпадает, а две другие нет.
C2
х
А2
N2
B2
D2
M2
K1
А1
С1
L2 (K2)
N1 , (M1
)
L1
D1
В1
На общей проекции одна точка загораживает другую – это
понятие называется – видимость точек.
Видима та точка, числовое значение координаты у которой

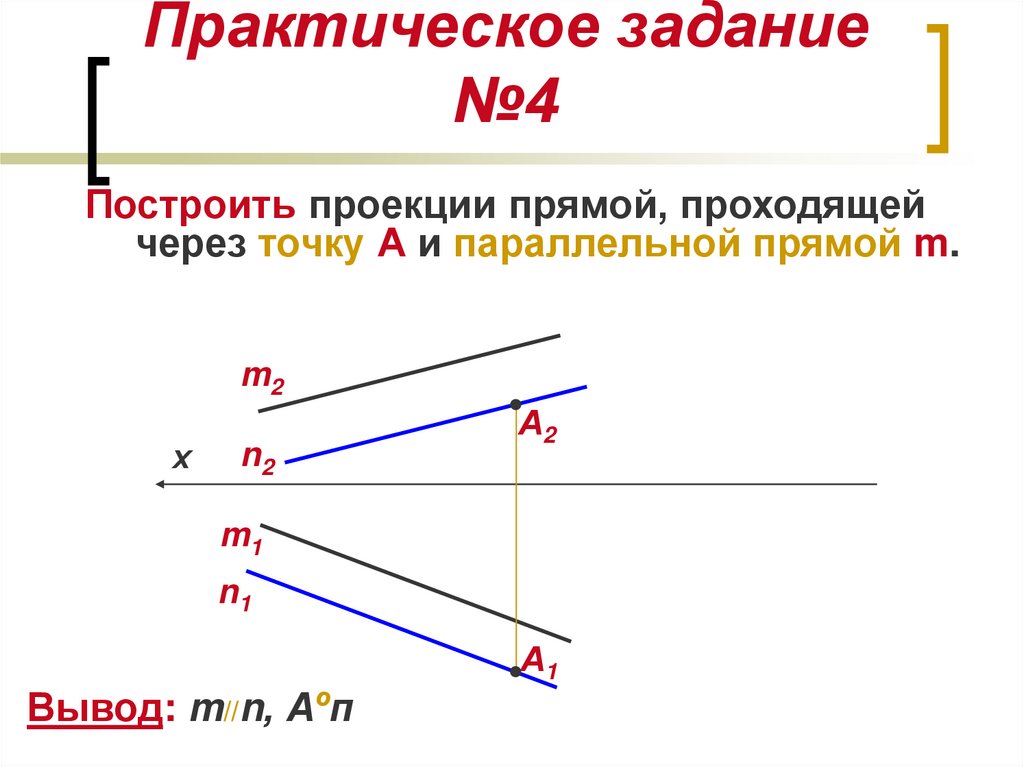
14. Практическое задание №4

Построить проекции прямой, проходящей
через точку А и параллельной прямой m.
m2
х
n2
А2
m1
n1
А1
Вывод: m//n, Аºп

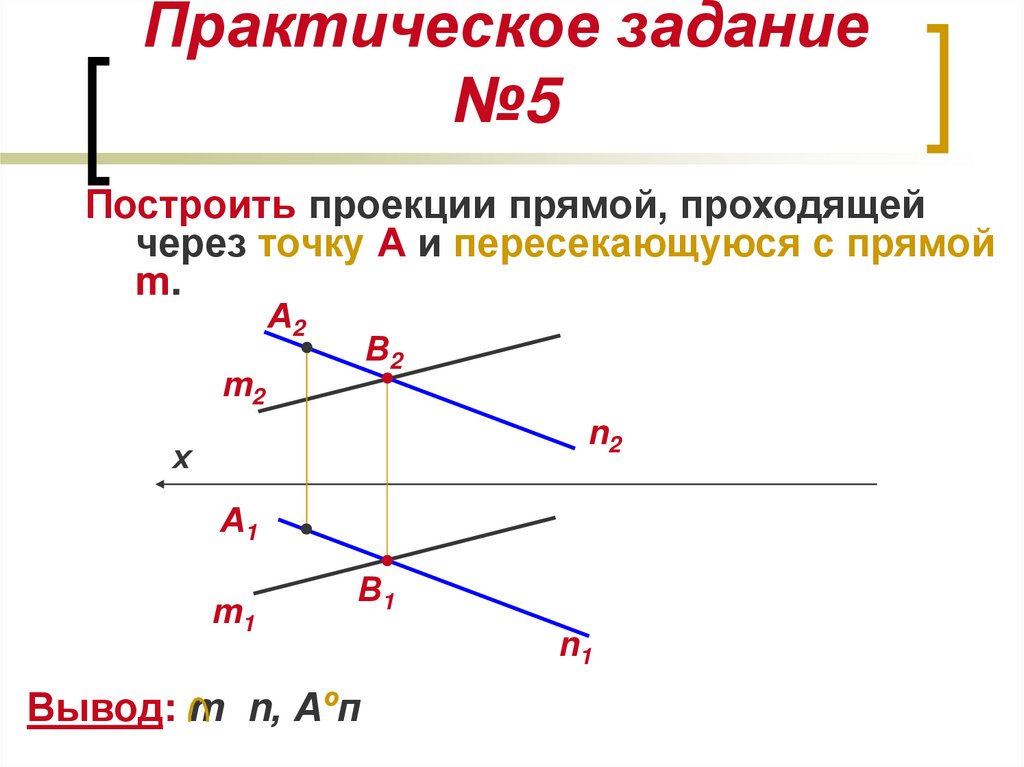
15. Практическое задание №5

Построить проекции прямой, проходящей
через точку А и пересекающуюся с прямой
m.
А2
В2
m2
n2
х
А1
m1
В1
Вывод: m n, Аºп
n1

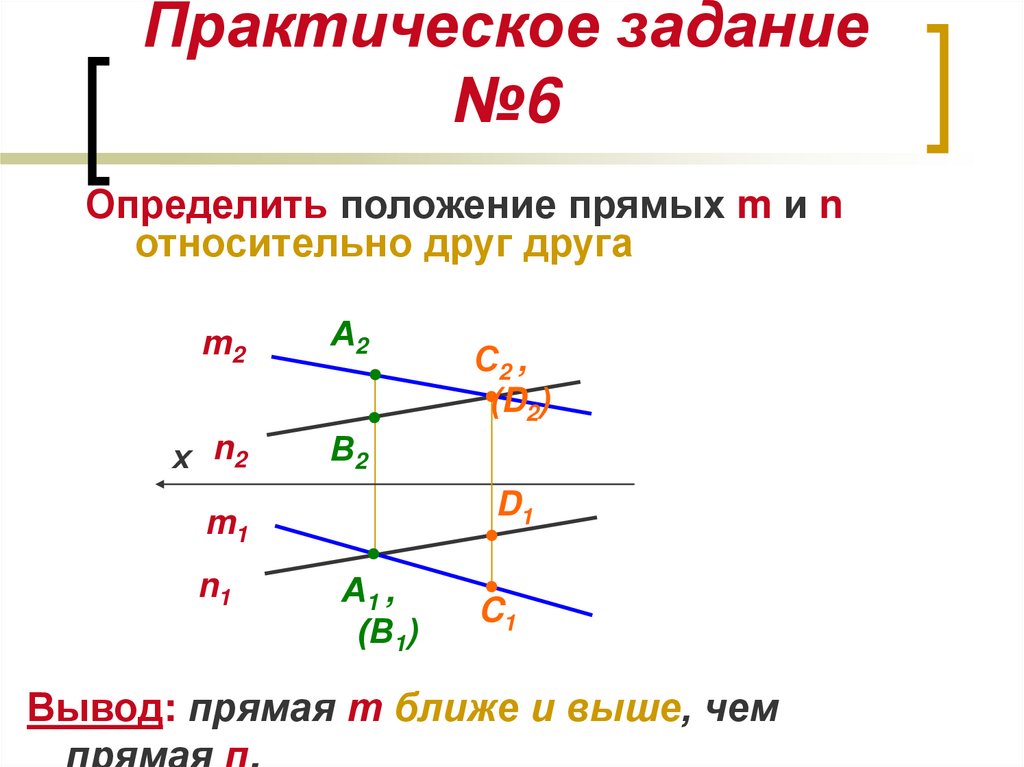
16. Практическое задание №6

Определить положение прямых m и n
относительно друг друга
m2
А2
х n2
В2
D1
m1
n1
С2 ,
(D2)
А1 ,
(В1)
C1
Вывод: прямая т ближе и выше, чем
прямая п.

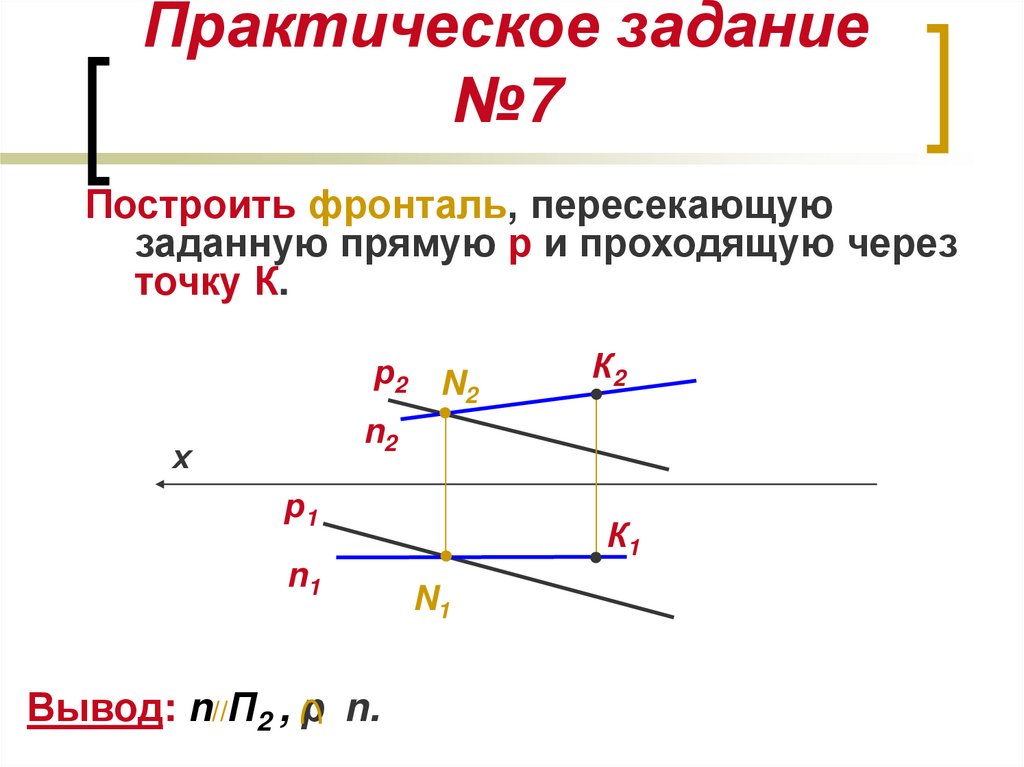
17. Практическое задание №7

Построить фронталь, пересекающую
заданную прямую р и проходящую через
точку К.
р2 N
2
n2
х
р1
n1
Вывод: n//П2 , р n.
К2
К1
N1

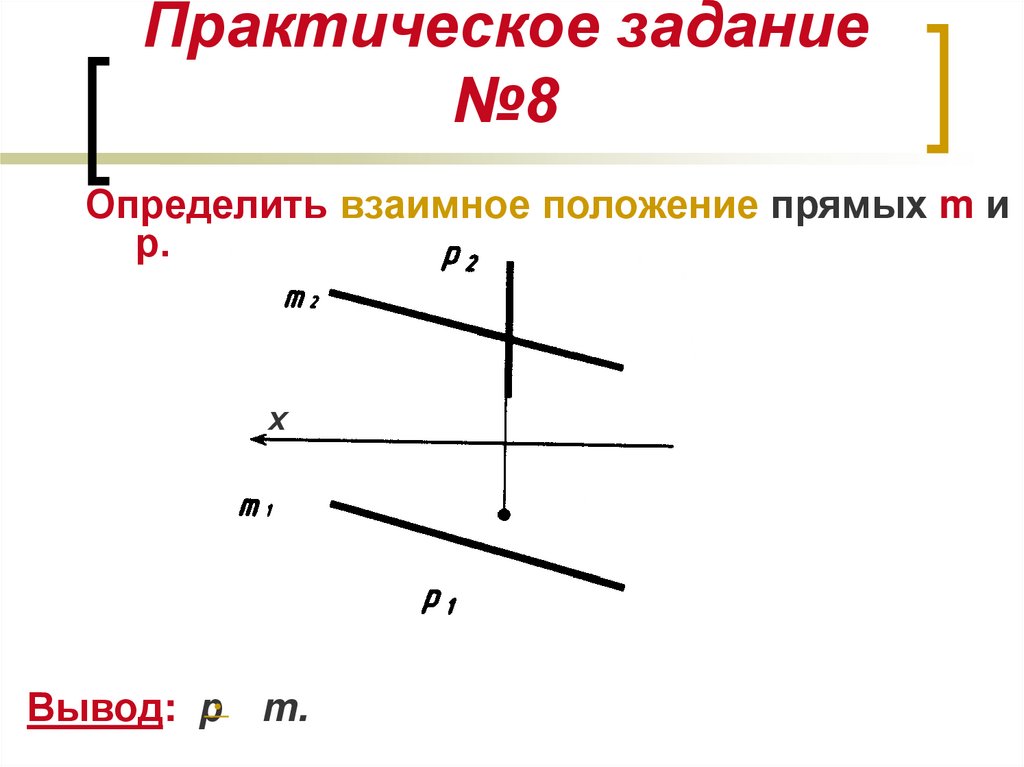
18. Практическое задание №8

Определить взаимное положение прямых m и
р.
х
Вывод: р m.

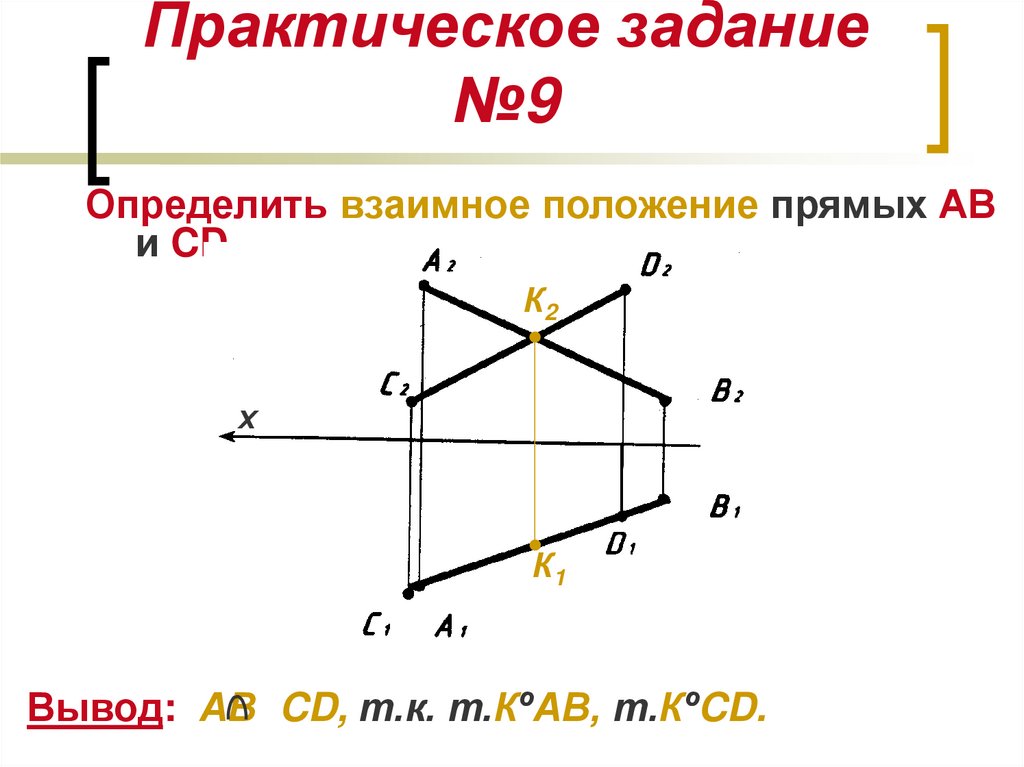
19. Практическое задание №9

Определить взаимное положение прямых АВ
и CD.
К2
х
К1
Вывод: АВ CD, т.к. т.КºАВ, т.КºCD.

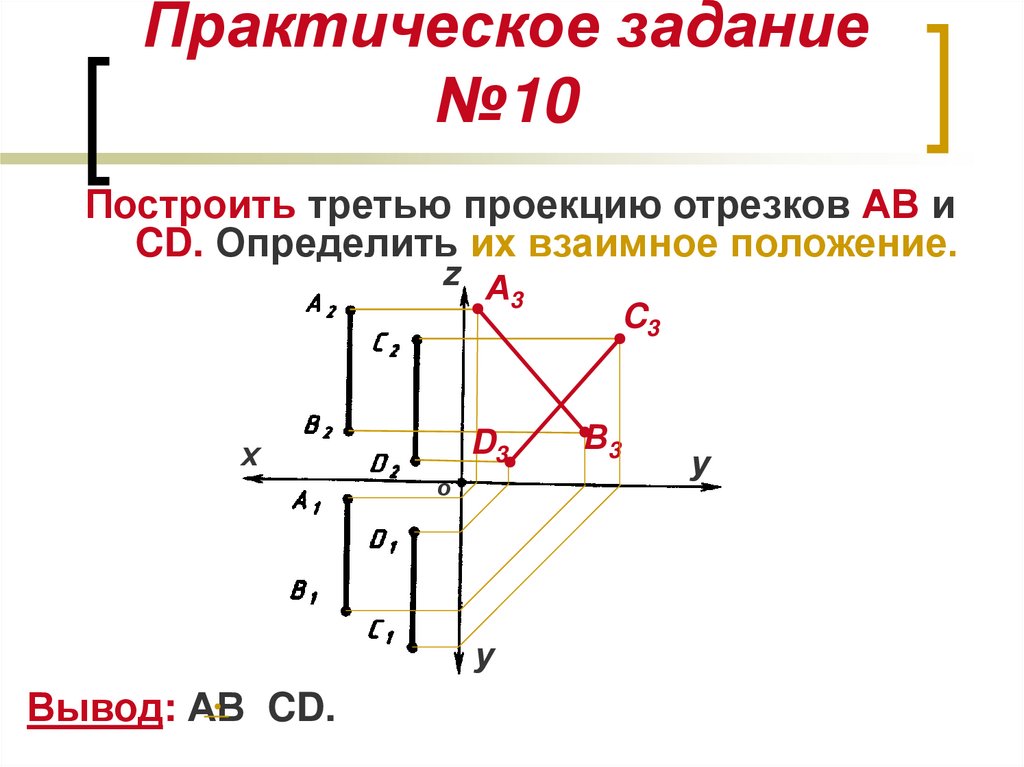
20. Практическое задание №10

Построить третью проекцию отрезков АВ и
CD. Определить их взаимное положение.
z А
3
D3
х
о
у
Вывод: АВ CD.
C3
В3
у