Similar presentations:
Решение простейших тригонометрических уравнений
1.
«Сегодня мы учимся вместе –Я, ваш учитель, и вы, мои ученики.
Но в будущем ученик должен
превзойти учителя, иначе в науке
не будет прогресса».
В.А.Сухомлинский
2.
3. Решение простейших тригонометрических уравнений.
Удачи!sin
tgx=
cos–xx1==1ctgx=0
0
Решение простейших
тригонометрических
уравнений.
4. Цели урока:
обобщить знания по теме «Решениепростейших тригонометрических
уравнений»,
проверить практические навыки и
умения учащихся при решении
уравнений,
научить применять знания, умения и
навыки в новой ситуации
5. Проверка домашнего задания.
• №1 Решить уравнение2
sin x
2
х ( 1)
к 1
4
к , к
6. №2
Найти корниуравнения
3
cos x
2
принадлежащие
промежутку [0;π]
5
х
2 к , к
6
к 0
5
х
6
к 1
17
х
6
7
х
6
5
Ответ :
6
7. №3
Найдите сумму корней уравненияctg x=-√3, принадлежащих промежутку
[-π;π]
5
х ( ) к
к, к
6
6
8.
5к
6
5
1 к 1
6
11
1
к
6
6
к 0; 1
5
х
6
х
6
Ответ :
5
2
6 6
3
9.
«Результат ученияравен
произведению
способности на
старательность.
Если старательность
равна нулю, то и
все произведение
равно нулю.
А способности есть у
каждого»
10. Это мы знаем…
• 1). Какое уравнение называетсятригонометрическим?
• 2).Уравнения какого вида
называются простейшими
тригонометрическими уравнениям?
• 3).Дайте определение арксинуса,
арккосинуса, арктангенса и
арккотангенса.
11. Вычислите:
1) sin 30 ; cos 90 ; tg 60 ; ctg 451
2) arcsin ; arccos 0; arctg1
2
2
1
1
arcsin
; arccos( ); arctg (
)
2
2
3
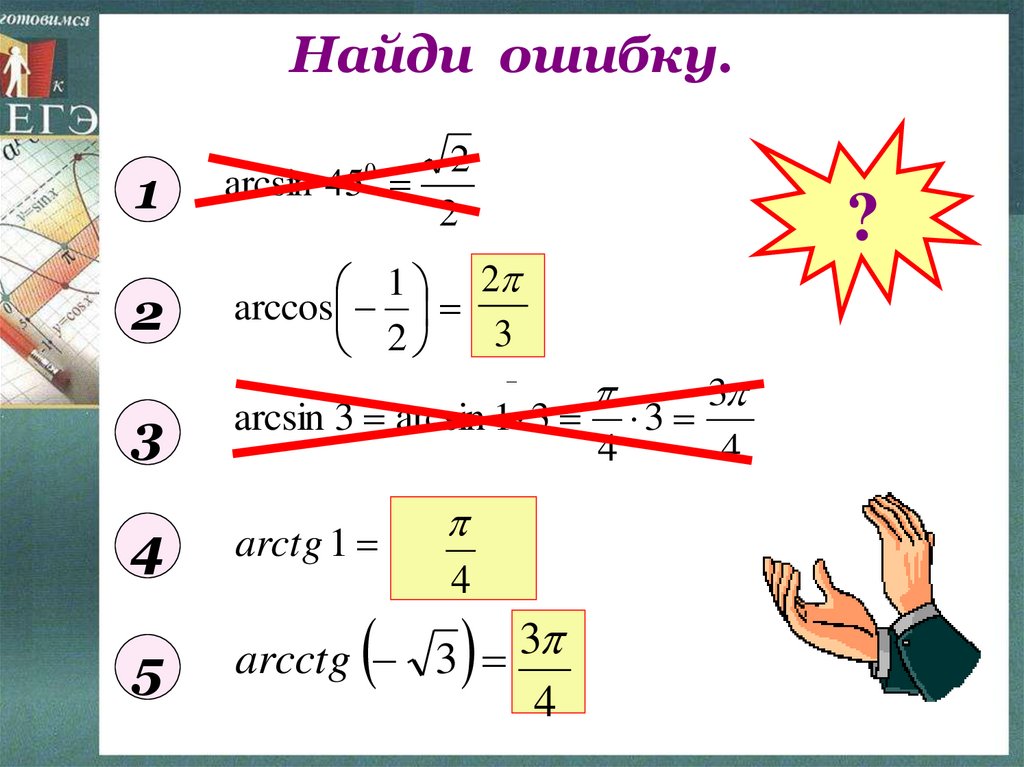
12. Найди ошибку.
12
arcsin 45
2
2
1 2
arccos
33
2
0
?
3
3
arcsin 3 arcsin 1 3 3
4
4
4
arctg 1 arctg
4 4
5
3
arcctg 3
46
13. Установите соответствие:
1sin x = 0
2
cos x = -1
3
sin x = 1
4
5
6
7
cos x = 1
tg x = 1
sin x = - 1
cos x = 0
2
2 k , k Z
k , k Z
2 k , k Z
2
2
k , k Z
2 k , k Z
2 k , k Z
4
k , k Z
14. Решение какого уравнения показано на тригонометрической окружности?
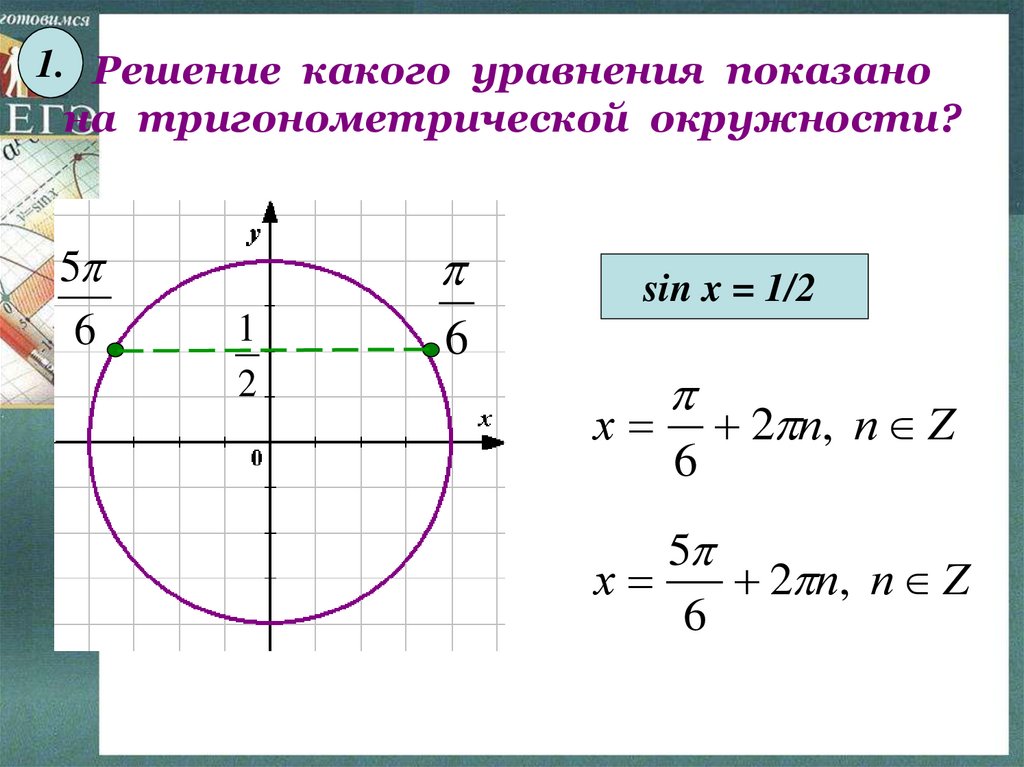
1. Решение какого уравнения показанона тригонометрической окружности?
5
6
1
2
6
sin x = 1/2
х
6
2 п, п Z
5
х
2 п, п Z
6
15. Решение какого уравнения показано на тригонометрической окружности?
2. Решение какого уравнения показанона тригонометрической окружности?
4
cos x = √2/2
х
2
2
4
х
4
4
2 п, п Z
2 п, п Z
16. Решение какого уравнения показано на тригонометрической окружности?
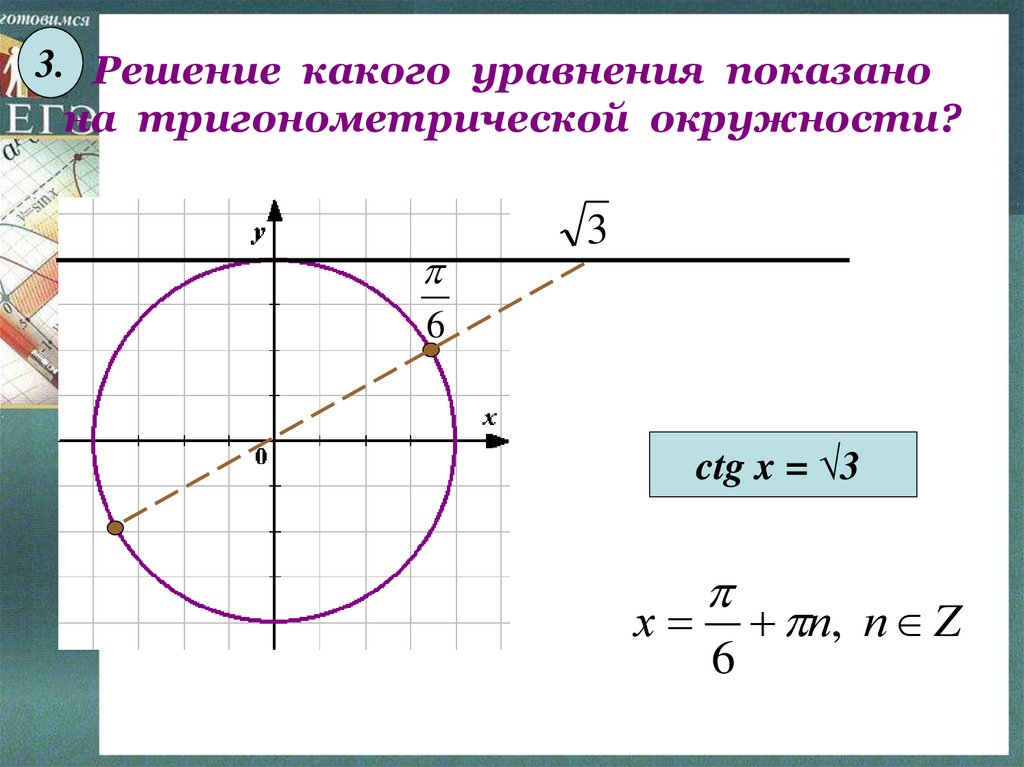
3. Решение какого уравнения показанона тригонометрической окружности?
6
3
ctg x = √3
х
6
п, п Z
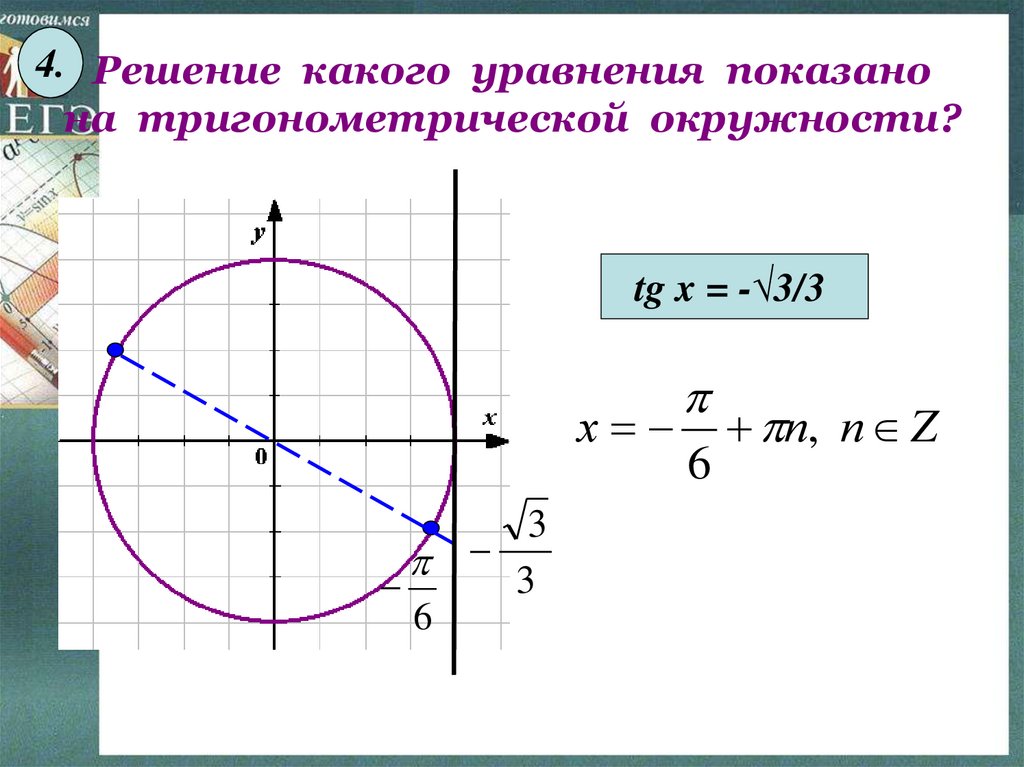
17. Решение какого уравнения показано на тригонометрической окружности?
4. Решение какого уравнения показанона тригонометрической окружности?
tg x = -√3/3
х
6
3
3
6
п, п Z
18. Проверочная работа.
Вариант 1.Вариант 2.
1. Каково будет решение
1. Каково будет решение
уравнения cos x = a при а > 1 уравнения sin x = a при а > 1
2. При каком значении а 2. При каком значении а
уравнение cos x = a имеет уравнение sin x = a имеет
решение?
решение?
3. Какой формулой
выражается это решение?
3. Какой формулой
выражается это решение?
4.
На какой оси откладывается
значение а при решении
уравнения cos x = a ?
4.
На какой оси откладывается
значение а при решении
уравнения sin x = a ?
19. Проверочная работа.
Вариант 1.Вариант 2.
5. В каком промежутке
находится arccos a ?
5. В каком промежутке
находится arcsin a ?
6. В каком промежутке
находится значение а?
6. В каком промежутке
находится значение а?
7. Каким будет решение
уравнения cos x = 1?
7. Каким будет решение
уравнения sin x = 1?
8. Каким будет решение
уравнения cos x = -1?
8. Каким будет решение
уравнения sin x = -1?
20. Проверочная работа.
Вариант 1.Вариант 2.
9. Каким будет решение
уравнения cos x = 0?
9. Каким будет решение
уравнения sin x = 0?
10. Чему равняется
arccos ( - a)?
10. Чему равняется
arcsin ( - a)?
11. В каком промежутке
находится arctg a?
11. В каком промежутке
находится arcctg a?
12. Какой формулой
выражается решение
уравнения tg x = а?
12. Какой формулой
выражается решение
уравнения сtg x = а?
21.
№1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
Вариант 1.
Нет решения
а 1
х arccos a 2 n, n Z
Вариант 2.
Нет решения
а 1
x 1 arcsin a k , k Z
n
На оси Ох
На оси Оу
1; 1
1; 1
0;
/ 2; /2
х 2 п, n Z
х / 2 2 k , k Z
х / 2 2 k , k Z
x 2 n, n Z
х k , k Z
x / 2 n, n Z
n arccos a
arcsin a
/ 2; / 2
0;
x arctg a n, n Z x arcctg a k , k Z
22.
А. Эйнштейн говорил так:“Мне приходится делить время между
политикой и уравнениями. Однако
уравнения, по-моему, гораздо важнее.
Политика существует только для
данного момента, а уравнения будут
существовать вечно”.
23. Как вы думаете, когда люди впервые столкнулись с тригонометрическими уравнениями?
24. «Исправьте ошибки на доске и подумайте об их причинах».
«Исправьте ошибки на доске иподумайте об их причинах».
Уравнение
Ответ с ошибкой Правильный ответ
1
cos x
2
x
3
sin x
2
x
1
sin 2 x
2
cos x
tgx
4
2 k , k z
3
3
2 k , k z
1
1
x ( ) k arcsin k , k z
2
2
10
3
10
x arccos
2 n, n z
3
x arctg
4
k , k z
x
3
x ( 1) k
x ( 1) k
2 k , k z
3
k , k z
12
k
2
,k z
нет
корней
x 1 k , k z
25. Страничка ЕГЭ.
• 1. Найти все корни уравнения7
10 cos ( x) sin(
2 x) 3,
2
2
2
которые удовлетворяют условию
2 19
x [ ;
].
3 12
26.
10 cos 2 (Пример . Найти все корни уравнения
2
которые удовлетворяют условию x [
Решение.
10sin2 x = – cos 2x + 3;
10sin2 x = 2sin2 x – 1 + 3,
8sin2 x = 2;
x) sin(
2 19
;
].
3 12
y
2
5
6
1
;
4
1
sin x ;
2
6
sin 2 x
0
7
6
k
x
(
1
)
k , k Z ,
6
x ( 1) m ( ) m, m Z ;
6
x
3
2
6
n, n Z ;
x
С помощью числовой окружности получим:
Ответ:
7
2 x) 3,
2
6
27.
Выберем корни, удовлетворяющие условию задачи2
19
Из первой серии:
n
,n Z;
3
6
12
8 2 12 n 19 , n Z ; (решая двойное неравенство)
10 12n 17, n Z .
Следовательно n=0 или n=1, то есть x ,
6
x 7 .
6
2
19
n
,n Z;
3
6
12
8 2 12 n 19 , n Z ;
Из второй серии:
6 12n 21, n Z .
Следовательно n=0 или n=1, то есть
Ответ : {
5 7
;
6 6
;
6
}.
x
,
6
x 5 .
6
28. 2) Решить уравнение
(3 cos x 4)( 2 sin x 1) 0б) Найдите все корни этого уравнения,
принадлежащие отрезку
5
;
2
29.
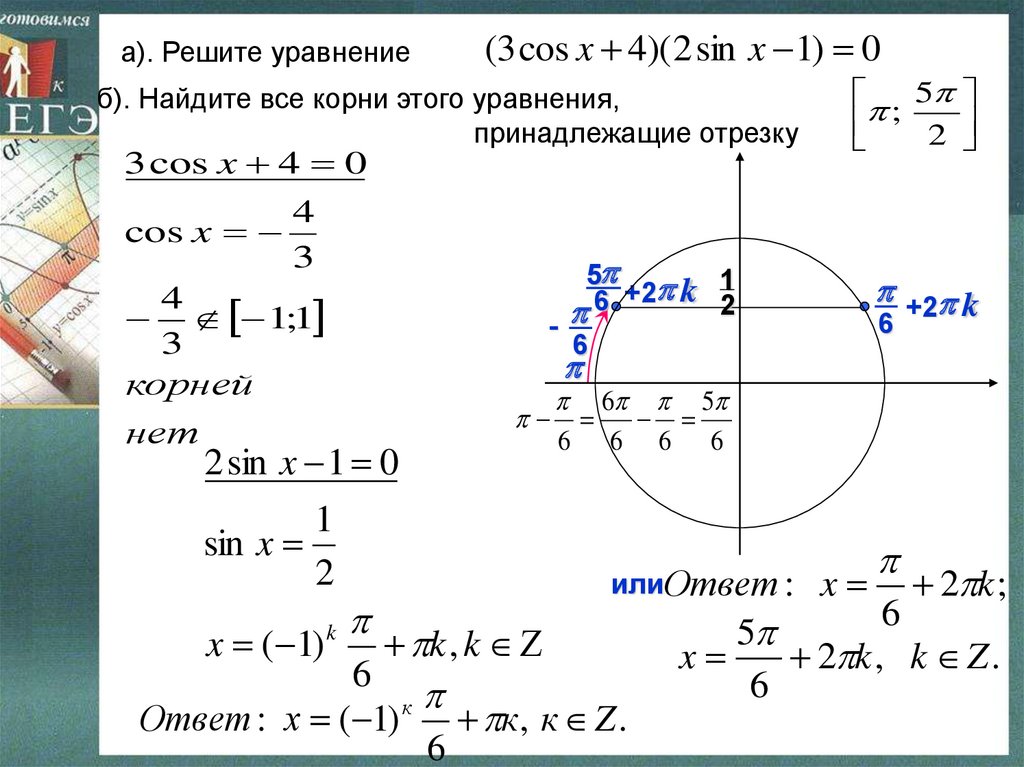
а). Решите уравнение(3 cos x 4)( 2 sin x 1) 0
б). Найдите все корни этого уравнения,
принадлежащие отрезку
3 cos x 4 0
cos x
4
3
5
+2 k 1
6
2
6
4
1;1
3
корней
нет
6 5
6 6 6 6
илиОтвет :
k , k
6
к
Ответ : х ( 1)
к , к Z .
6
x ( 1)
k
+2 k
6
2 sin x 1 0
1
sin x
2
5
;
2
x
2 k ;
6
5
x
2 k , k Z .
6
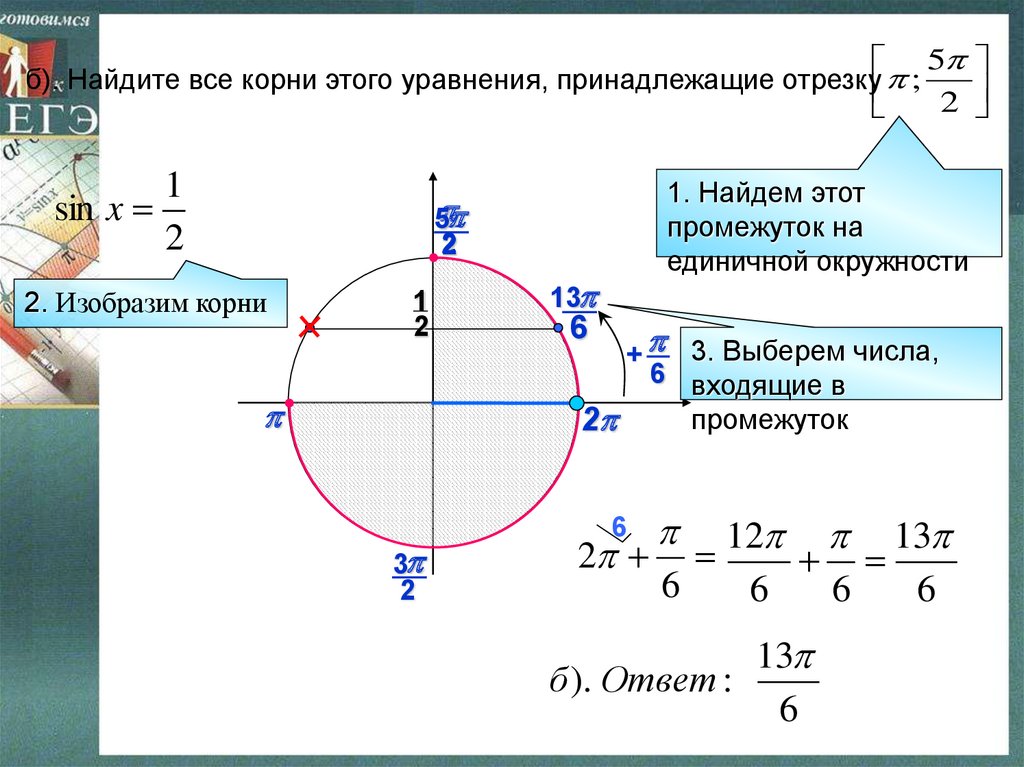
30.
5б). Найдите все корни этого уравнения, принадлежащие отрезку ;
2
1
sin x
2
1. Найдем этот
промежуток на
единичной окружности
5
2
2. Изобразим корни
1
2
3
2
13
6
+ 3. Выберем числа,
6 входящие в
промежуток
2
6
2
6
12 13
6
6
6
13
б ). Ответ :
6
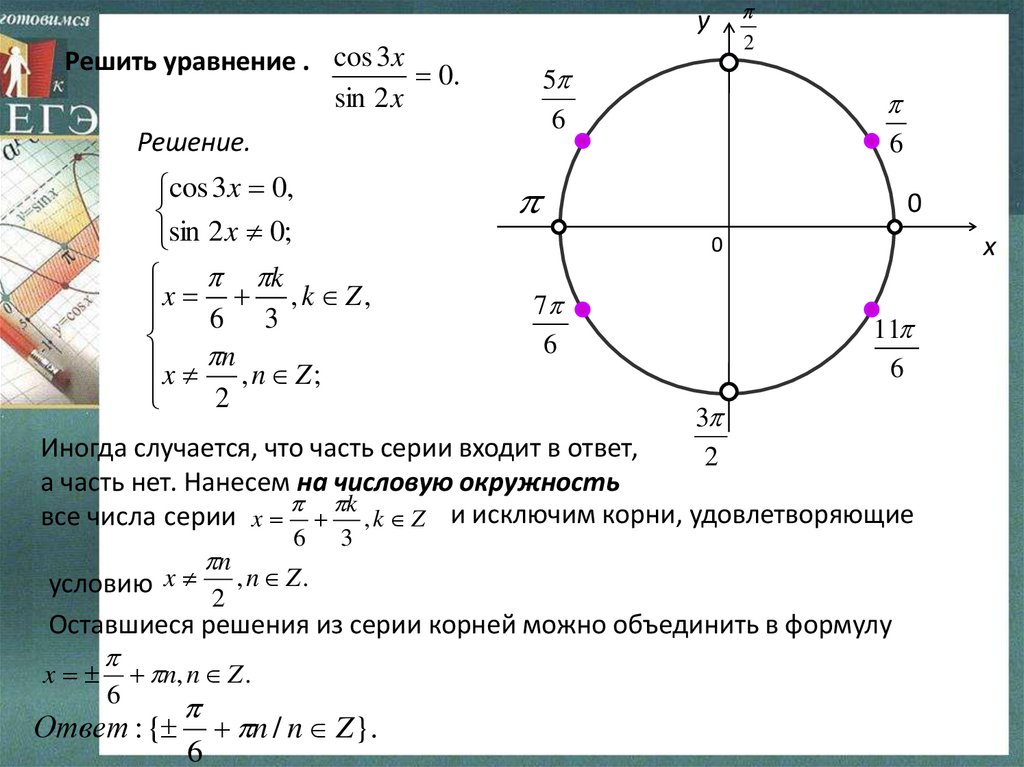
31. 3.Решить уравнение:
cos 3 x0.
sin 2 x
32.
2y
Решить уравнение . cos 3 x 0.
sin 2 x
5
6
Решение.
cos 3x 0,
sin 2 x 0;
6
k
x
,k Z,
6 3
x n , n Z ;
2
0
x
0
7
6
11
6
3
2
Иногда случается, что часть серии входит в ответ,
а часть нет. Нанесем на числовую окружность
все числа серии x k , k Z и исключим корни, удовлетворяющие
условию x
n
2
6
3
, n Z.
Оставшиеся решения из серии корней можно объединить в формулу
x n, n Z .
6
Ответ : {
6
n / n Z }.
33. Домашнее задание:
№ 897,898,899(2,4)
стр. 293
34.
зу
х
35.
« СЧИТАЙ НЕСЧАСТНЫМ ТОТ ДЕНЬ ИЛИЧАС, В КОТОРЫЙ ТЫ НЕ УСВОИЛ НИЧЕГО
НОВОГО И НИЧЕГО НЕ ПРИБАВИЛ К
СВОЕМУ ОБРАЗОВАНИЮ»
Я. А. КАМЕНСКИЙ.




























 mathematics
mathematics








