Решение тригонометрических уравнений

1.

Учиться можно только
весело…
Чтобы переваривать
знания, надо поглощать
их с аппетитом.
Анатоль Франс
1844 - 1924

2. Решение тригонометрических уравнений.

Удачи!
sin
4x
–
sin
2x
=
0
sincos
x =x 1= 0
Решение
тригонометрических
уравнений.
ГБОУ СОШ №654
г.Москва, 20 декабря, 10 класс

3. Угадайте слово

Из чисел вы мой первый слог возьмите,
Второй из слова «гордецы».
А третьим лошадей вы погоните,
Четвертым будет блеянье овцы.
Мой пятый слог такой же, как и первый,
Последней буквой в алфавите является
шестой,
А если отгадаешь ты все верно,
То в математике раздел получишь ты
такой.

4. Разминка

• Какие из формул записаны неверно:

5. Проверочная работа.

Вариант 1.
Вариант 2.
1. Каково будет решение
1. Каково будет решение
уравнения cos x = a при а > 1 уравнения sin x = a при а > 1
2. При каком значении а 2. При каком значении а
уравнение cos x = a имеет уравнение sin x = a имеет
решение?
решение?
3. Какой формулой
выражается это решение?
3. Какой формулой
выражается это решение?
4.
На какой оси откладывается
значение а при решении
уравнения cos x = a ?
4.
На какой оси откладывается
значение а при решении
уравнения sin x = a ?

6. Проверочная работа.

Вариант 1.
Вариант 2.
5. Каким будет решение
уравнения cos x = 1?
5. Каким будет решение
уравнения sin x = 1?
6. Каким будет решение
уравнения cos x = -1?
6. Каким будет решение
уравнения sin x = -1?
7. Каким будет решение
уравнения cos x = 0?
7. Каким будет решение
уравнения cos x = 0?
8. Какой формулой
выражается решение
уравнения tg x = а?
8. Какой формулой
выражается решение
уравнения сtg x = а?

7.

№
1.
2.
3.
Вариант 1.
Нет решения
а 1
х arccos a 2 n, n Z
Вариант 2.
Нет решения
а 1
x 1 arcsin a k , k Z
n
4.
На оси Ох
5.
х / 2 2 k , k Z
х 2 п, n Z
х / 2 2 k , k Z
x 2 n, n Z
x / 2 n, n Z х k , k Z
x arctg a n, n Z x arcctg a k , k Z
6.
7.
8.
На оси Оу

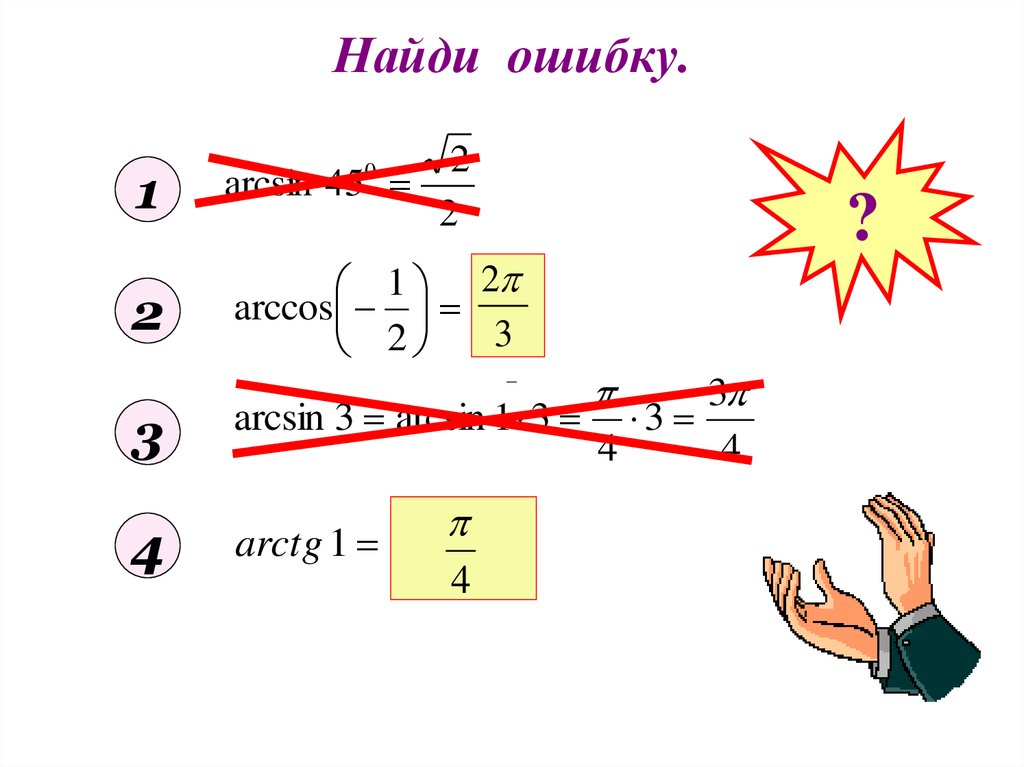
8. Найди ошибку.

1
2
arcsin 45
2
2
1 2
arccos
33
2
0
?
3
3
arcsin 3 arcsin 1 3 3
4
4
4
arctg 1 arctg
4 4

9. Тест

10. Решение какого уравнения показано на тригонометрической окружности?

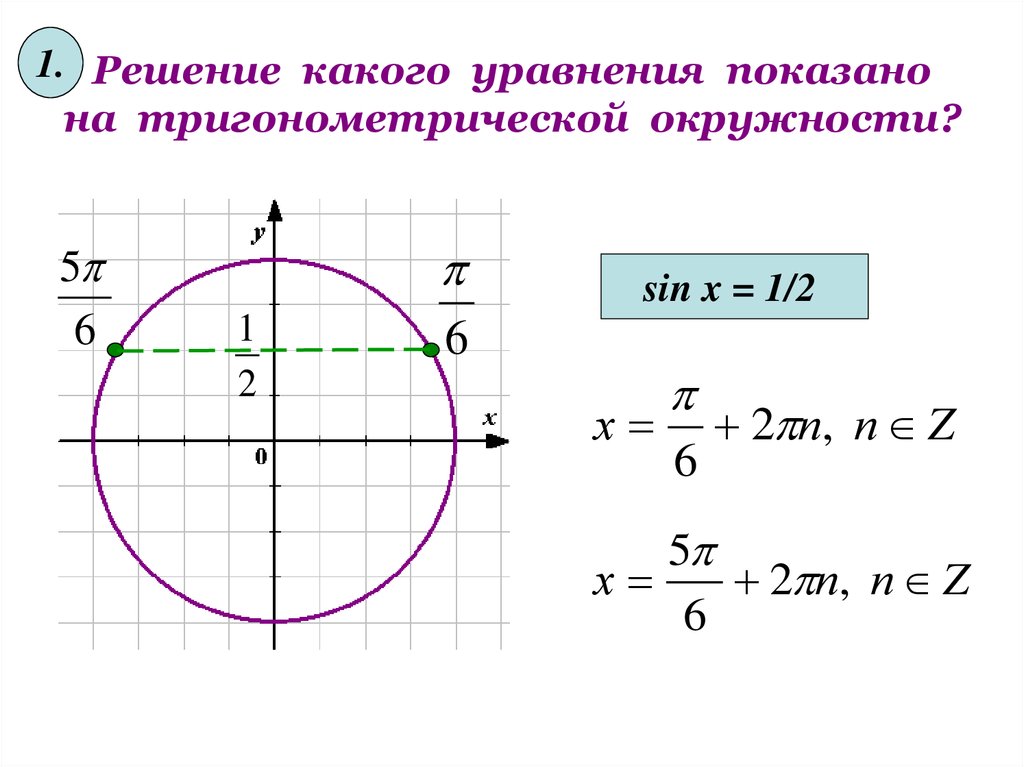
1. Решение какого уравнения показано
на тригонометрической окружности?
5
6
1
2
6
sin x = 1/2
х
6
2 п, п Z
5
х
2 п, п Z
6

11. Решение какого уравнения показано на тригонометрической окружности?

2. Решение какого уравнения показано
на тригонометрической окружности?
4
cos x = √2/2
х
2
2
4
х
4
4
2 п, п Z
2 п, п Z

12. Решение какого уравнения показано на тригонометрической окружности?

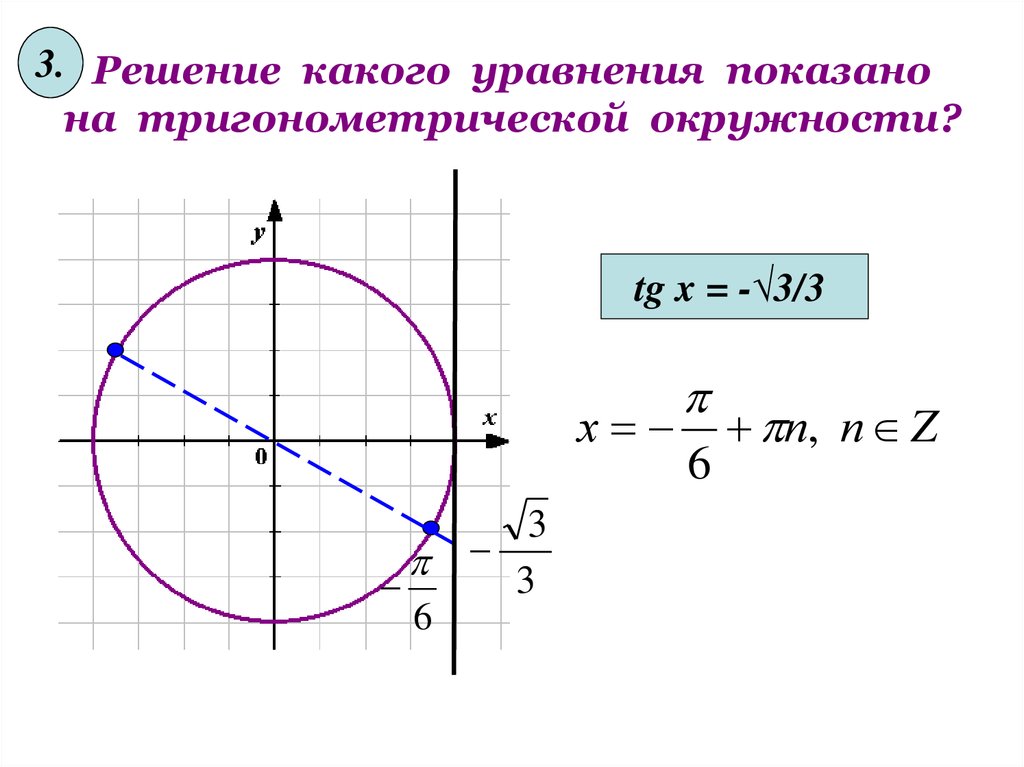
3. Решение какого уравнения показано
на тригонометрической окружности?
tg x = -√3/3
х
6
3
3
6
п, п Z

13. Решение какого уравнения показано на тригонометрической окружности?

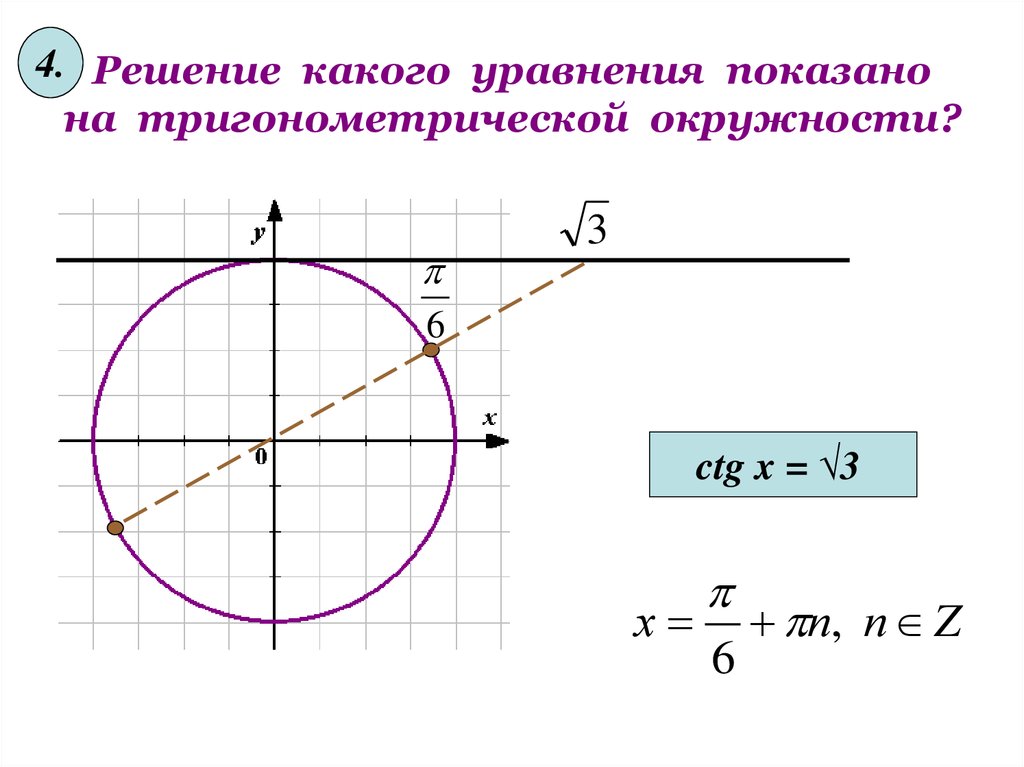
4. Решение какого уравнения показано
на тригонометрической окружности?
6
3
ctg x = √3
х
6
п, п Z

14.

1.Сводимые к квадратным
a∙sin²x + b∙sinx + c=0
Пусть sinx = p, где |p| ≤1, тогда
a∙p² + b∙p + c = 0
Найти корни, вернуться к замене и
решить простые уравнения.
2.Однородные
1)Первой степени:
a∙sinx + b∙cosx = 0
Т.к. sinx и cosx одновременно
не равны нулю, то разделим обе
части уравнения на cosx. Получим:
простое уравнение
a∙tgx + b = 0 или tgx = m
2)Второй степени:
a∙sin²x + b∙sinx∙cosx + c∙cos²x = 0
Разделим обе части на cos²x.
Получим квадратное уравнение:
a∙tg²x + b∙tgx + c = 0.

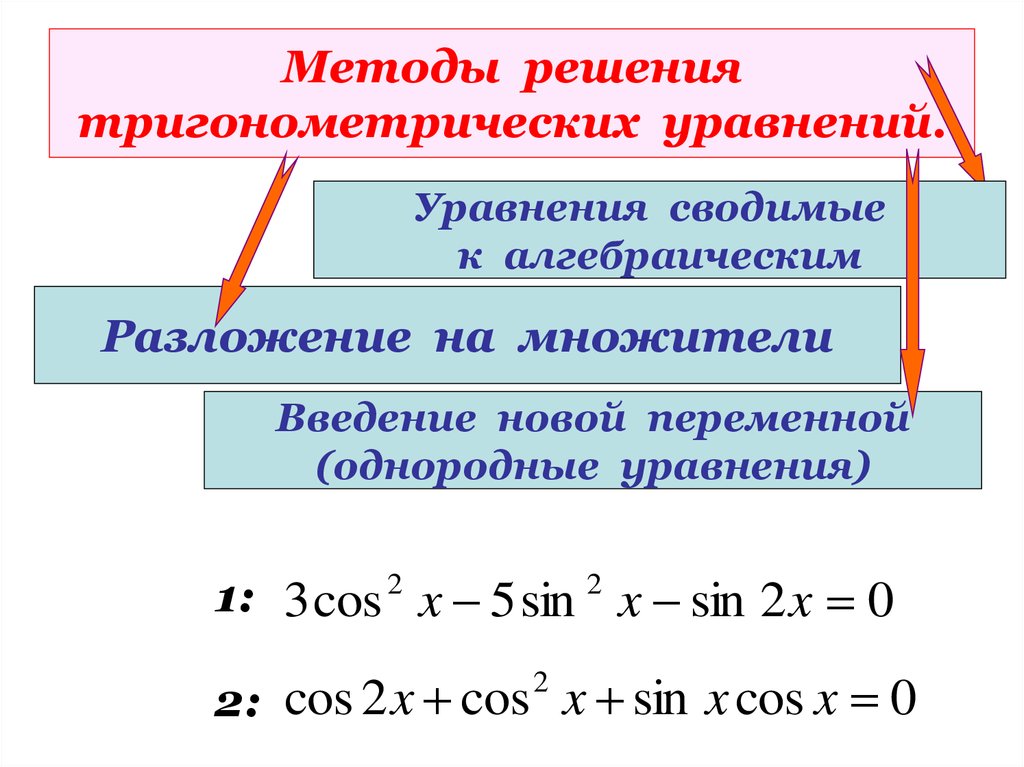
15. Методы решения тригонометрических уравнений.

Уравнения сводимые
к алгебраическим.
1:
cos 2 x sin x sin x 0,25
2:
3 cos 2x 5 cos x 1
2

16. Методы решения тригонометрических уравнений.

Уравнения сводимые
к алгебраическим
Разложение на множители
1:
3 sin x 3 sin x cos x 0
2:
3 cos x 3 sin x cos x 0
2
2

17. Методы решения тригонометрических уравнений.

Уравнения сводимые
к алгебраическим
Разложение на множители
Введение новой переменной
(однородные уравнения)
1: 3 cos 2 x 5 sin 2 x sin 2 x 0
2: cos 2 x cos x sin x cos x 0
2

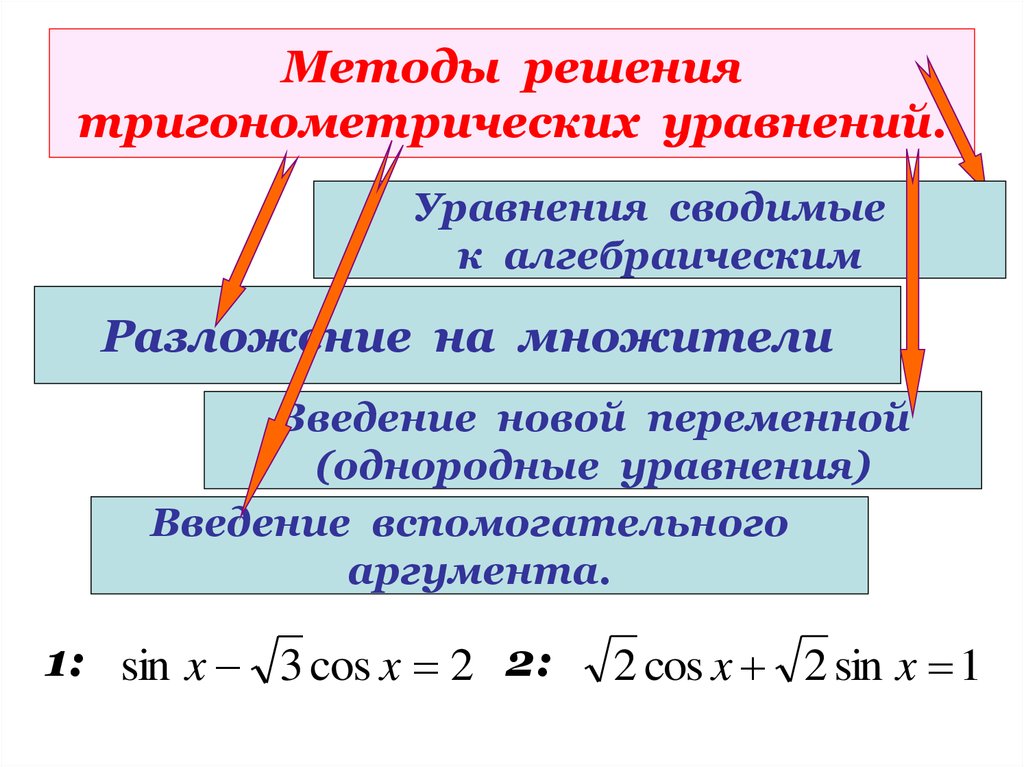
18. Методы решения тригонометрических уравнений.

Уравнения сводимые
к алгебраическим
Разложение на множители
Введение новой переменной
(однородные уравнения)
Введение вспомогательного
аргумента.
1: sin x 3 cos x 2 2:
2 cos x 2 sin x 1

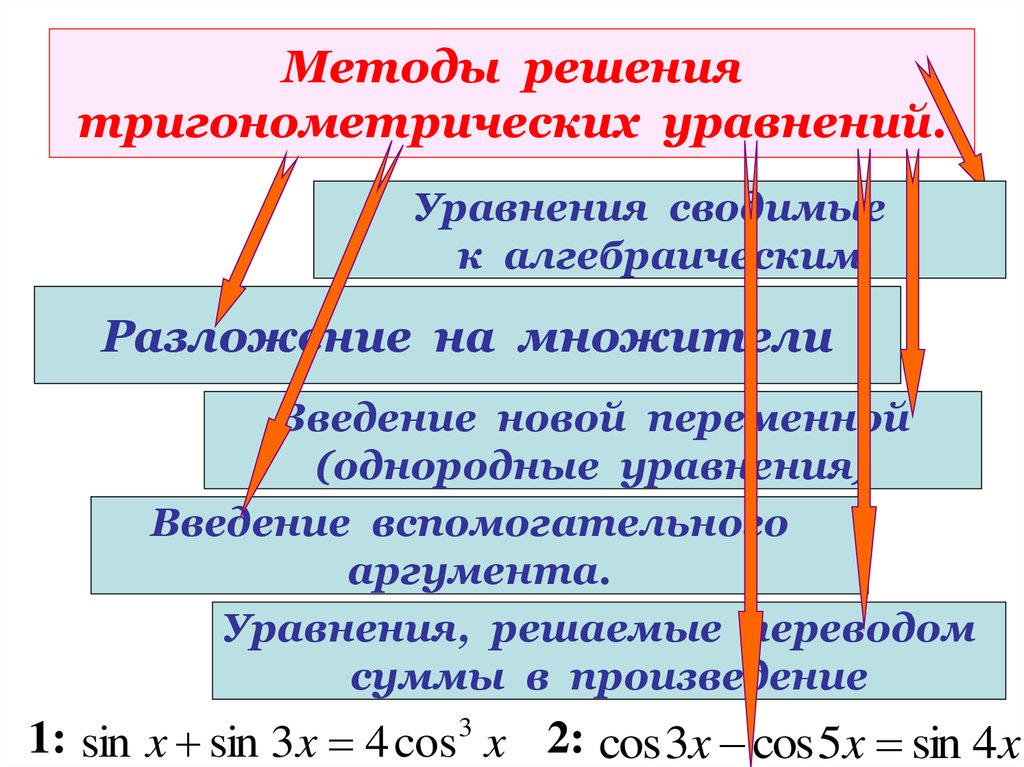
19. Методы решения тригонометрических уравнений.

Уравнения сводимые
к алгебраическим
Разложение на множители
Введение новой переменной
(однородные уравнения)
Введение вспомогательного
аргумента.
Уравнения, решаемые переводом
суммы в произведение
1: sin x sin 3x 4 cos3 x 2: cos 3x cos 5x sin 4x

20.

Решить уравнения
1. 2 cos2x + 3 sin x = 0
2. sin 2x + sin x = 0
3. (1 – cos 2x)(tg x -1 ) = 0
4. tg x – 2 ctg x + 1 = 0
5. 2 cos2x + 5 sin x + 1 = 0
6.3 sin2x – 4sinxcosx + cos2x =0
7. sinx + cosx =1

21.

1. sin x = a
2. cos x = a
3. tg x = a
4. ctg x = a
5. sin x = 1
6. cos x = 1
7. sin x =- 1
8. cos x =- 1
9. sin x = 0
10. cos x = 0
Е X = ± arccos a + 2Пn
О x = П/2 + 2Пn
Р X = 2Пn
В X = (- 1)n arcsin a + Пn
Е X = - П/2 + 2Пn
Р X = arctg a + Пn
Ш X = П + 2Пn
Л x = Пn
Н X = arcctg a + Пn
И X = П/2 + Пn

22. Ребусы

. … — это ___________________ … — это ___________________
Подсказка. Если около рисунка стоит зачеркнутая буква и рядом с ней написана другая, то это значит, что в слове нужно произвести замену одной буквы на другую.

23. Предлагаю задания, связанные с символом наступающего 2014 года. 2014 год - год синей деревянной лошади. Этот год несет в себе

динамизм и напористость, сочетание расчетливости и огненной
страсти.
Лошадь гнедой масти
Корпус и голова коричневого окраса различных оттенков.
Хвост, грива и конечности ниже скакательных и запястных
суставов — черные. На корпусе тоже присутствует
небольшая примесь черных волос.
Задача № 1. Умер старик и оставил трем своим сыновьям
17 лошадей. А перед смертью распорядился,
чтобы они поделили табун так, чтобы
старший взял половину всех лошадей,
средний — треть и младший — девятую часть
всех лошадей. Старик умер и оставил 17 лошадей.
Начали сыновья дележ, но число 17 не делится
ни на 2, ни на 3, ни на 9. Как им быть?
Обратились братья к мудрецу. Тот приехал к ним
на собственной лошади и разделил все по завещанию.
Как он это сделал?

24.

МОЛОДЦЫ!