Similar presentations:
Решение тригонометрических уравнений
1.
Учиться можно тольковесело…
Чтобы переваривать
знания, надо поглощать
их с аппетитом.
Анатоль Франс
1844 - 1924
2. Решение тригонометрических уравнений.
Удачи!sin 4x sin
– sin
2x1 = 0
x
=
cos x = 0
Решение
тригонометрических
уравнений.
3. Проверочная работа.
Вариант 1.Вариант 2.
1. Каково будет решение
1. Каково будет решение
уравнения cos x = a при а > 1 уравнения sin x = a при а > 1
. При каком значении а
уравнение cos x = a имеет
ешение?
2. При каком значении а
уравнение sin x = a имеет
решение?
3. Какой формулой
выражается это решение?
3. Какой формулой
выражается это решение?
4.
На какой оси откладывается
значение а при решении
уравнения cos x = a ?
4.
На какой оси откладывается
значение а при решении
уравнения sin x = a ?
4. Проверочная работа.
Вариант 1.Вариант 2.
5. В каком промежутке
находится arccos a ?
5. В каком промежутке
находится arcsin a ?
6. В каком промежутке
находится значение а?
6. В каком промежутке
находится значение а?
7. Каким будет решение
уравнения cos x = 1?
7. Каким будет решение
уравнения sin x = 1?
8. Каким будет решение
уравнения cos x = -1?
8. Каким будет решение
уравнения sin x = -1?
5. Проверочная работа.
Вариант 1.Вариант 2.
9. Каким будет решение
уравнения cos x = 0?
9. Каким будет решение
уравнения sin x = 0?
10. Чему равняется
arccos ( - a)?
10. Чему равняется
arcsin ( - a)?
11. В каком промежутке
находится arctg a?
11. В каком промежутке
находится arcctg a?
12. Какой формулой
выражается решение
уравнения tg x = а?
12. Какой формулой
выражается решение
уравнения сtg x = а?
6.
№1.
2.
3.
Вариант 1.
Нет решения
а 1
х arccos a 2 n, n Z
Вариант 2.
Нет решения
а 1
x 1 arcsin a k , k Z
На оси Оу
n
4.
На оси Ох
5.
0;
/ 2; /2
6.
1; 1
1; 1
7.
8.
9.
10.
х 2 п, n Z
x 2 n, n Z
x / 2 n, n Z
n arccos a
11.
/ 2; / 2
12.
x arctg a n, n Z
х / 2 2 k , k Z
х / 2 2 k , k Z
х k , k Z
arcsin a
0;
x arcctg a k , k Z
7. Найди ошибку.
12
arcsin 45
2
2
1 2
arccos
33
2
3
3
arcsin 3 arcsin 1 3 3
4
4
4
arctg 1 arctg
4 4
5
0
arcctg
3
3
46
?
8. Какая из схем лишняя?
12
3
4
5
6
9. Какие из схем лишние?
12
3
4
5
6
10. Установите соответствие:
1sin x = 0
2
cos x = -1
3
sin x = 1
4
cos x = 1
5
tg x = 1
6
7
sin x = - 1
cos x = 0
2 k , k Z
2
2 k , k Z
k , k Z
k , k Z
2
2 k , k Z
2
2 k , k Z
k , k Z
4
11. Установите соответствие:
1sin x = 0
2
cos x = -1
3
sin x = 1
4
cos x = 1
5
tg x = 1
6
7
sin x = - 1
cos x = 0
2 k , k Z
2
2 k , k Z
k , k Z
k , k Z
2
2 k , k Z
2
2 k , k Z
k , k Z
4
12. Решение какого уравнения показано на тригонометрической окружности?
1. Решение какого уравнения показанона тригонометрической окружности?
5
6
1
2
6
sin x = 1/2
х 2 п, п Z
6
5
х 2 п, п Z
6
13. Решение какого уравнения показано на тригонометрической окружности?
2. Решение какого уравнения показанона тригонометрической окружности?
4
2
2
cos x = √2/2
х 2 п, п Z
4
4
х 2 п, п Z
4
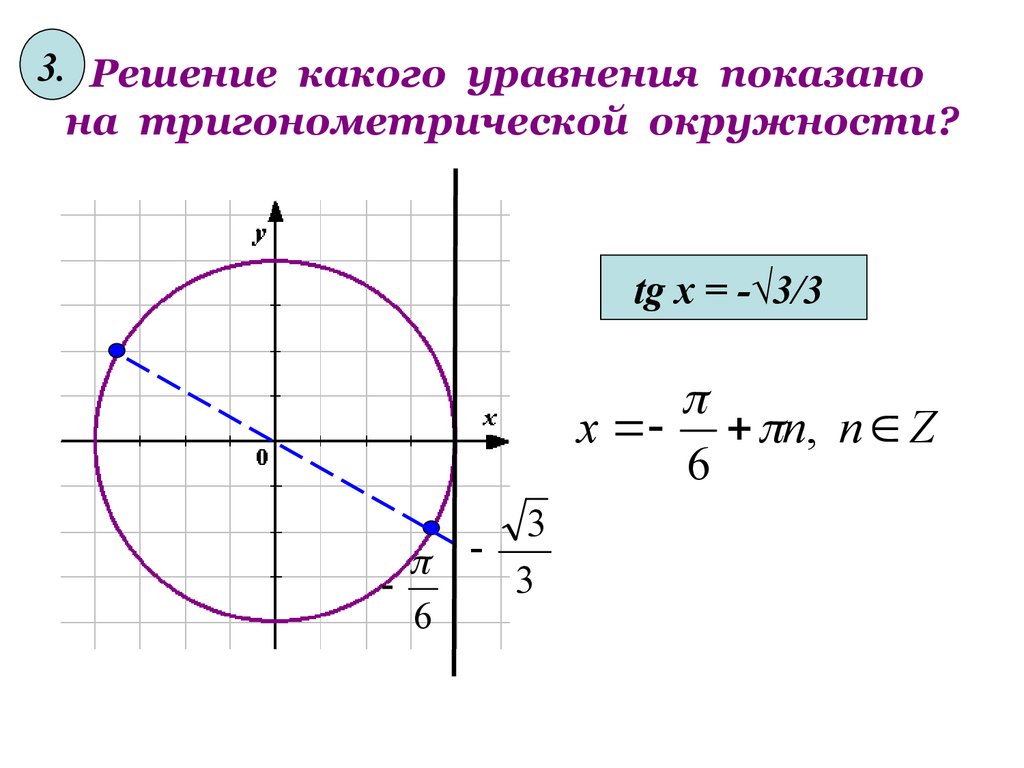
14. Решение какого уравнения показано на тригонометрической окружности?
3. Решение какого уравнения показанона тригонометрической окружности?
tg x = -√3/3
х п, п Z
6
3
3
6
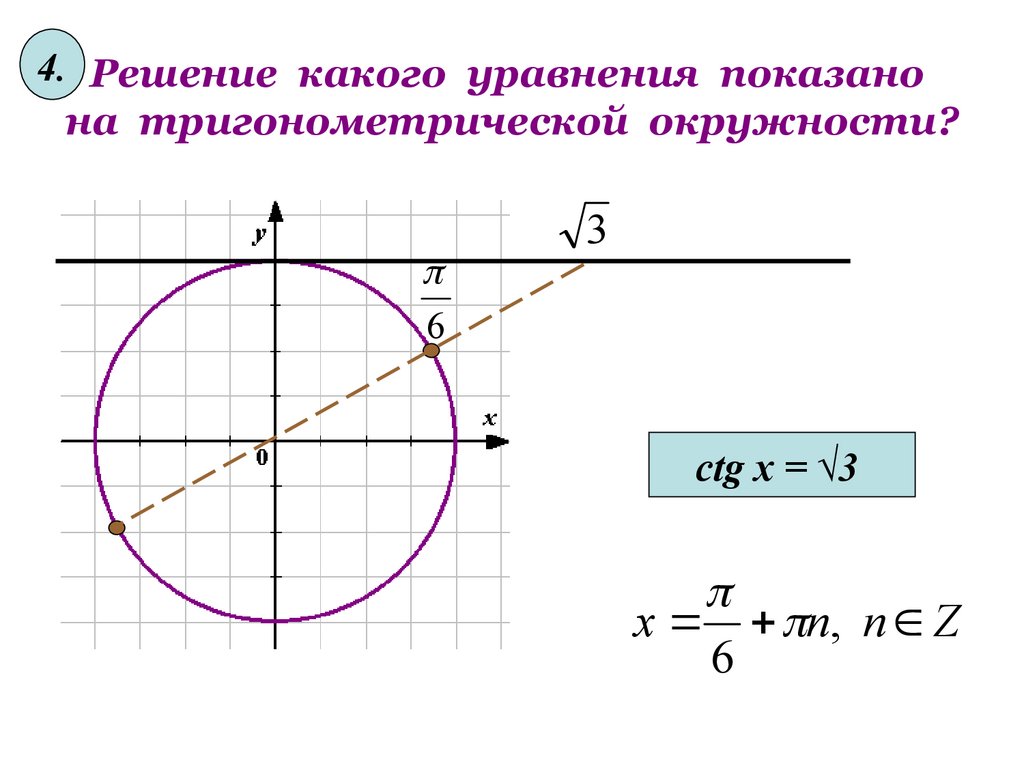
15. Решение какого уравнения показано на тригонометрической окружности?
4. Решение какого уравнения показанона тригонометрической окружности?
6
3
ctg x = √3
х п, п Z
6
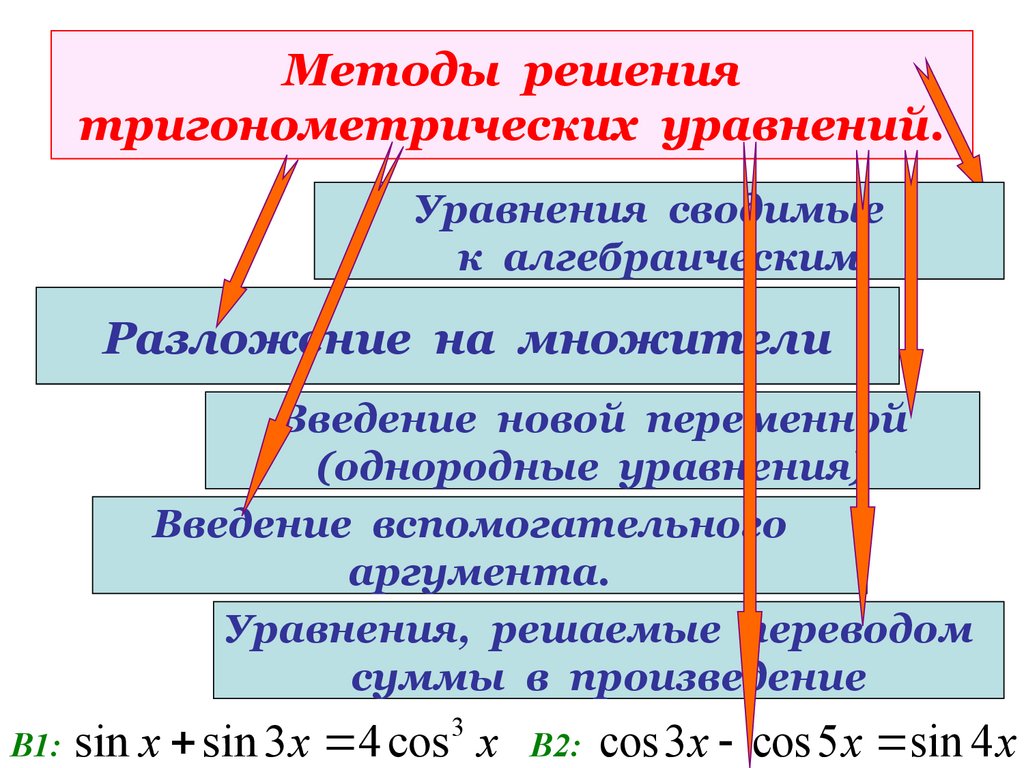
16. Методы решения тригонометрических уравнений.
Необходимо выбрать соответствующийМетоды решения
прием для решения уравнений.
тригонометрических уравнений.
Уравнения сводимые
к алгебраическим.
2
Вариант 1:
cos 2 x sin x sin x 0,25
Вариант 2:
3 cos 2 x 5 cos x 1
17. Методы решения тригонометрических уравнений.
Уравнения сводимыек алгебраическим
Разложение на множители
Вариант 1:
Вариант 2:
2
3 sin x
2
3 sin x cos x 0
3 cos x 3 sin x cos x 0
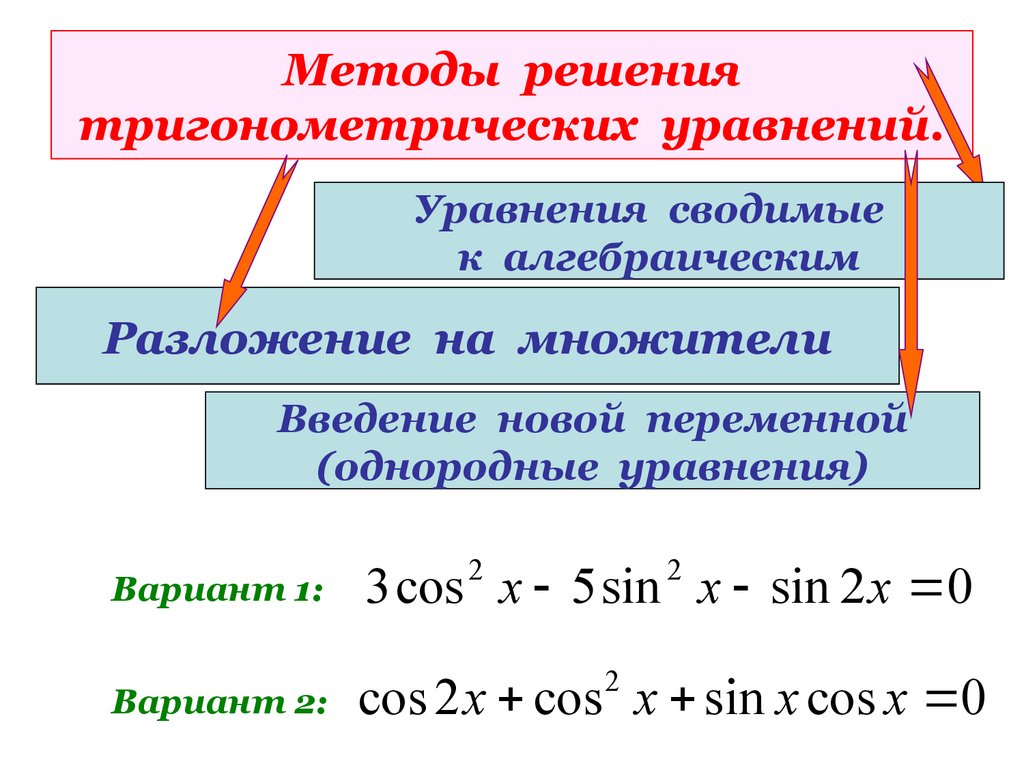
18. Методы решения тригонометрических уравнений.
Уравнения сводимыек алгебраическим
Разложение на множители
Введение новой переменной
(однородные уравнения)
Вариант 1:
Вариант 2:
2
2
3 cos x 5 sin x sin 2 x 0
2
cos 2 x cos x sin x cos x 0
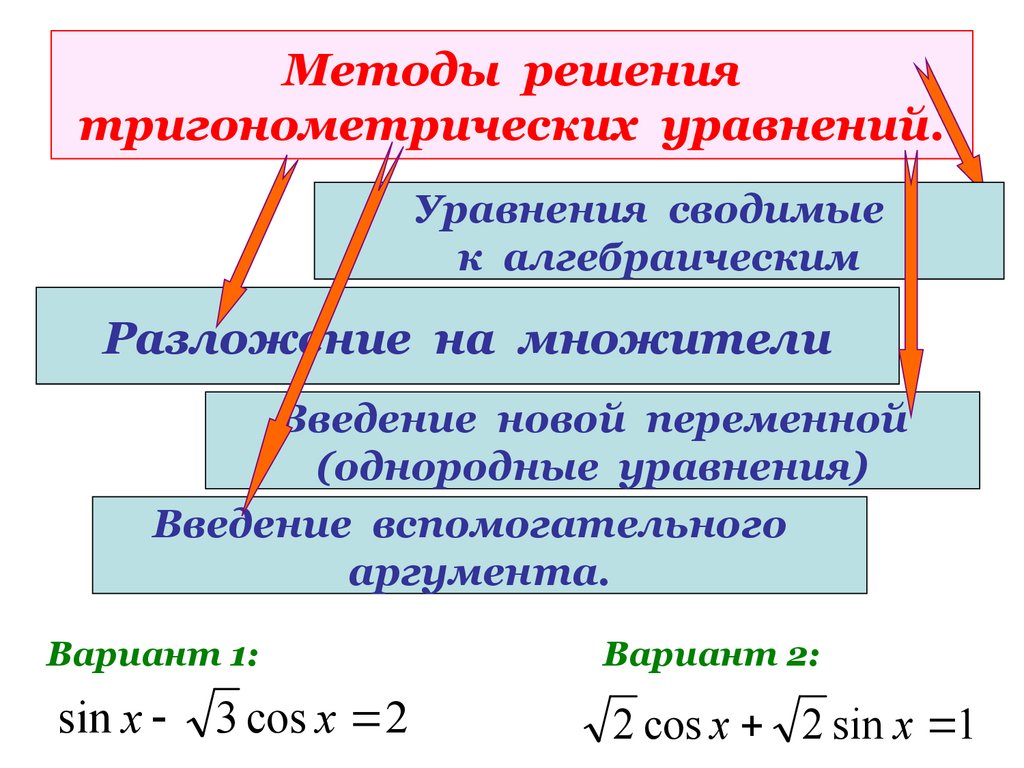
19. Методы решения тригонометрических уравнений.
Уравнения сводимыек алгебраическим
Разложение на множители
Введение новой переменной
(однородные уравнения)
Введение вспомогательного
аргумента.
Вариант 1:
sin x
3 cos x 2
Вариант 2:
2 cos x 2 sin x 1
20. Методы решения тригонометрических уравнений.
Уравнения сводимыек алгебраическим
Разложение на множители
Введение новой переменной
(однородные уравнения)
Введение вспомогательного
аргумента.
Уравнения, решаемые переводом
суммы в произведение
В1:
sin x sin 3x 4 cos3 x
В2:
cos 3x cos 5 x sin 4 x
21. Формулы квадрата половинных углов:
Применение формул понижениястепени.
Формулы квадрата половинных углов:
1 cos
1 cos
2
2
cos
sin
2
2
2
2
Формулы понижения степени:
1
cos 1 cos 2
2
1
sin 1 cos 2
2
2
2
2sin2 x + cos 4x = 0
В1:
2
2
2
sin x sin 2 x sin 3x 1,5
В2:
2
2
2
cos x cos 2 x cos 3x 1,5
22. Домашнее задание:
№ 207 (а, б, в, д)стр. 389

















 mathematics
mathematics








